基于多项式回归分析的机械臂架系统计算模型构建

朱 奇

ZHU Qi

(湖南工业职业技术学院 机械工程学院,长沙 410208)

0 引言

臂架是挖掘机、起重机、混凝土泵车等诸多工程机械装备中常用的一种重要结构形式[1]。臂架系统的臂架长度、臂架结构重量、臂架静、动态总弯矩等主要参数决定着产品的整机重量、整机稳定性及其他主要部件的设计，在超长臂架混凝土泵车、长臂架举高消防车、长臂架高空作业平台等高端装备的设计开发中，臂架系统的主要参数尤为重要。目前此类工程机械产品常规的设计思路是从臂架系统的详细设计开始，然后根据臂架系统的主要参数确定整机参数与整机方案，最后进行其他部件的设计。这种方法在产品设计初期，由于臂架系统主要参数的未知，会导致总体方案与其他部件方案设计时存在较大的不确定性，后期反复修改的可能性较大；而且在臂架系统设计时不能同时进行其他部件以及液压与电控方案的设计，使得产品设计开发周期较长，设计人员工作量较大。其实这些产品在很多企业都是系列化产品，如果在已有系列化臂架系统数据的基础上，提前预测新臂架系统的参数，为整机方案及其他部件方案的设计提供依据和参考，将会大大缩短产品的设计开发周期。

回归分析是指一种利用所观测的数据来拟合系统反映系统固有规律的数学模型的方法。它寻求存在于两个（或多个）变量之间的关系，解决或者预测生产、生活等存在的问题和规律。回归分析方法广泛应用于各个领域，在工业设计中在产品的概念设计阶段，特别是在已经系列化产品设计中，设计人员如果能根据已有产品的各种性能参数拟合系统的数学模型，找出系统满足的固有规律，然后预测待设计产品的各种性能参数，对于设计工作有重要的指导意义。多项式回归分析是研究一个因变量与一个或多个自变量间多项式关系的一种回归分析方法（polynomial regression）[2]。本文根据臂架系统的特点使用多项式回归分析方法建立机械臂架系统主要参数的数学模型，预测臂架系统中臂架长度、臂架重量、臂架静态弯矩等参数的内在规律，并与常规精确设计方法得到的臂架系统参数进行对比，验证模型的可靠性，为工程设计人员进行臂架系统设计、产品总体方案设计、整机性能评估及其他主要部件设计提供参考和依据。

1 多项式回归模型的构建

根据Taylor公式任何函数f(x)多可展开为一个关于x的多项式，为了简化计算过程在实际应用中多利用多项式来拟合实验数据[2，3]。从数据集中取N个数据样本（xi，yi）（i=1，2，…，N）中拟合k阶多项式的回归观测值可表示为：

则样本点i残差可表示为：

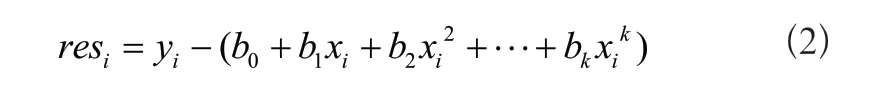
假设resi～N（0，бi）即样本点i 残差满足均值为ц=0 方差б=бi正态分布且相互独立，则（res1，res2，...，resn）的联合概率密度为：

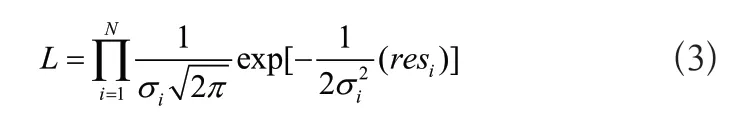
要使函数L取最大值，即要求式(2)最小化，由于

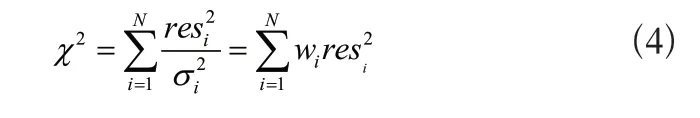
当取бi=1进行等权重拟合，最后估计参数b的矩阵形式可表示为：

其中

残差平方和可表示为

拟合的标准偏差为：

其中df=n-（k+1）

可根据式(8)中的sd判断所得多项的优劣。

臂架系统中有臂架长度、臂架重量、臂架静、动态弯矩等主要参数。在工程实际应用中，一般最关心臂架长度与臂架重量、臂架长度与臂架静态弯矩的关系，如果要对这些参数进行回归分析，必须建立起多变量测量的数学模型。若已知臂架长度与臂架重量，臂架长度与臂架静态总弯矩的若干组数据xi，yi（i=0，1，2，...，n）的值，则可以求出多项式的系数ai（i=0，1，2，...，n），从而可以分别得到近似的表示臂架长度与臂架重量，臂架长度与臂架静态总弯矩的多项式表达式：y=f（x）=a0+a1x+a2x2+...+anxn，模型中可以通过增加x的高次项对实测点进行逼近，直至满意为止。

2 臂架系统多项式回归分析

本文将根据某A、B两公司提供的各种型号臂架数据，分别拟合两公司的臂架长度与臂架结构重量、臂架长度与静态总弯矩的数学模型，并利用所得模型预测新型号混凝土泵车臂架结构重量及静态总弯矩，并使用拟合的标准偏差和判定系数评判数学模型的最优化。

2.1 混凝土泵车臂架系统组成

混凝土泵车臂架系统主要由臂节、油缸、连杆、输送管组成。臂节是臂架系统的主要部分，一般用高强钢板焊接而成箱梁式结构，臂架系统从底部向上各节臂分别命名为1节臂至第N节臂，第1节臂支撑在转台上。臂架工作工况是由各节臂在空间中所处位置确定的，如图1所示，其俯仰运动由一套举臂油缸来完成，泵车臂架在工作中所受的载荷主要是外部载荷和自身质量[4]。

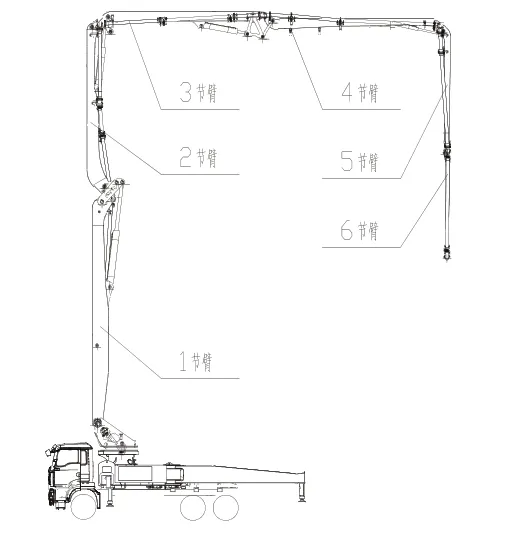
图1 混凝土泵车臂架系统组成

2.2 混凝土泵车臂架系统主要参数

表1、表2分别为A、B公司不同型号混凝土泵车臂架长度、臂架结构重量、臂架静态弯矩（结构件重量+混凝土重量）的数据表。

表1 A公司各型号泵车臂架系统参数

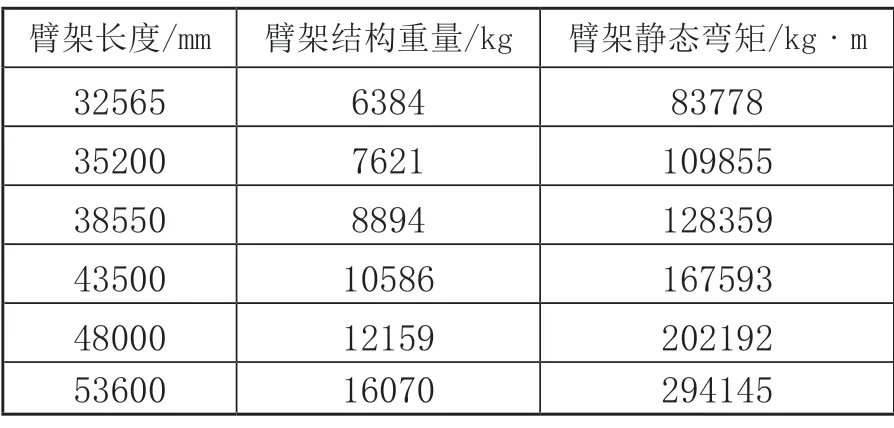
表2 B公司各型号泵车臂架系统参数

图2、图3分别为两公司混凝土泵车臂架系统三个主要参数的变化分布图，从图中可以看出，臂架系统的三个主要参数之间并不满足典型的线性关系，如果要依据现有臂架系统主要参数为参考开发新产品，需要对各参数进行数学建模和拟合分析。

图2 A公司各型号泵车臂架系统参数变化

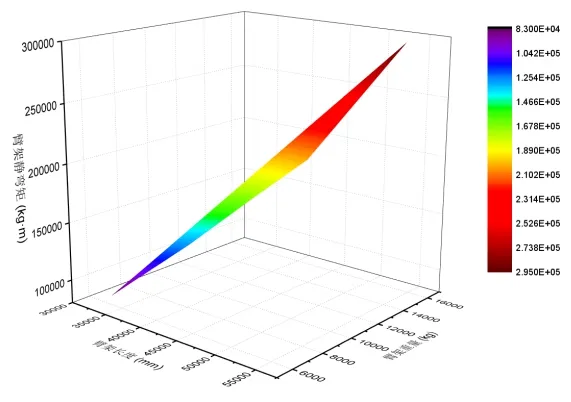
图3 B公司各型号泵车臂架系统参数变化

2.3 混凝土泵车臂架系统回归分析

在origin中分别对两公司的臂架长度与臂架重量、臂架静态总弯矩进行多项式拟合分析和建模。表3为臂架公司臂架长度与臂架重量、静态总弯矩三阶多项式拟合表，表中拟合出了前三阶函数。从表中可看出，2阶臂架重量函数标准偏差为280.8546，为三阶臂重函数中最小，而拟合判定系数为0.99605，为阶臂重函数中最高，说明2阶臂架重量函数为臂架长度与臂架重量最佳拟合模型。同样，2阶臂架静态总弯矩函数标准偏差为280.8546，为三阶静态弯矩函数中最小，而拟合判定系数为0.99605，为三阶静态弯矩函数中最高，说明2阶臂架静态总弯矩函数为臂架长度与臂架静态总弯矩最佳拟合模型。图4为A公司臂长—臂重关系曲线与二阶拟合曲线；图5为A公司臂长—臂架静态总弯矩关系与二阶拟合曲线。

图4 臂长—臂重关系曲线与二阶拟合曲线

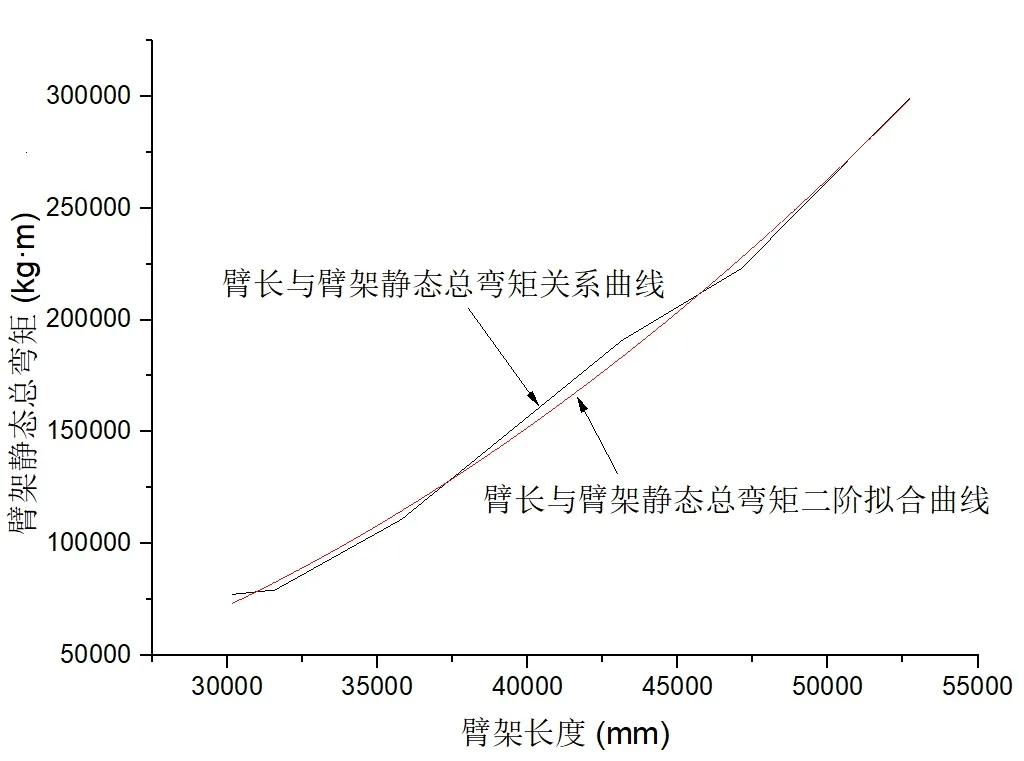
图5 臂长—臂架静态总弯矩关系与二阶拟合曲线

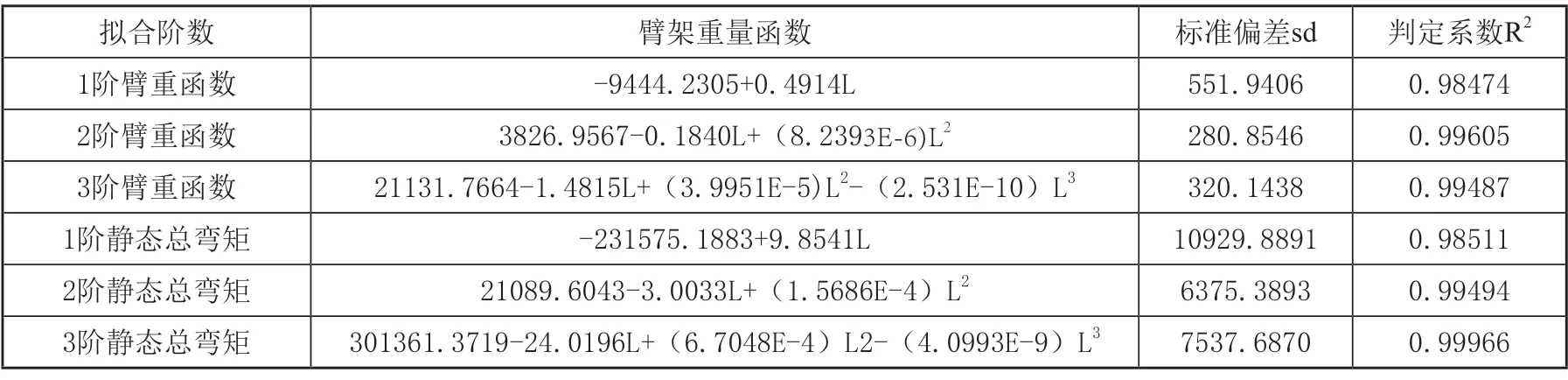
表3 A公司臂架长度与臂架重量、静态总弯矩多项式拟合表

表4为B公司臂架长度与臂架重量、静态总弯矩三阶多项式拟合表，表中拟合出了前三阶函数。从表中可看出，3阶臂架重量函数标准偏差为116.15187，为三阶臂重函数中最小，而拟合判定系数为0.9989，为阶臂重函数中最高，说明3阶臂架重量函数为臂架长度与臂架重量最佳拟合模型。同样，3阶臂架静态总弯矩函数标准偏差为4168.9138，为三阶静态弯矩函数中最小，而拟合判定系数为0.99701，为三阶静态弯矩函数中最高，说明3阶臂架静态总弯矩函数为臂架长度与臂架静态总弯矩最佳拟合模型。图6为B公司臂长—臂重关系曲线与三阶拟合曲线；图7为B公司臂长—臂架静态总弯矩关系与三阶拟合曲线。

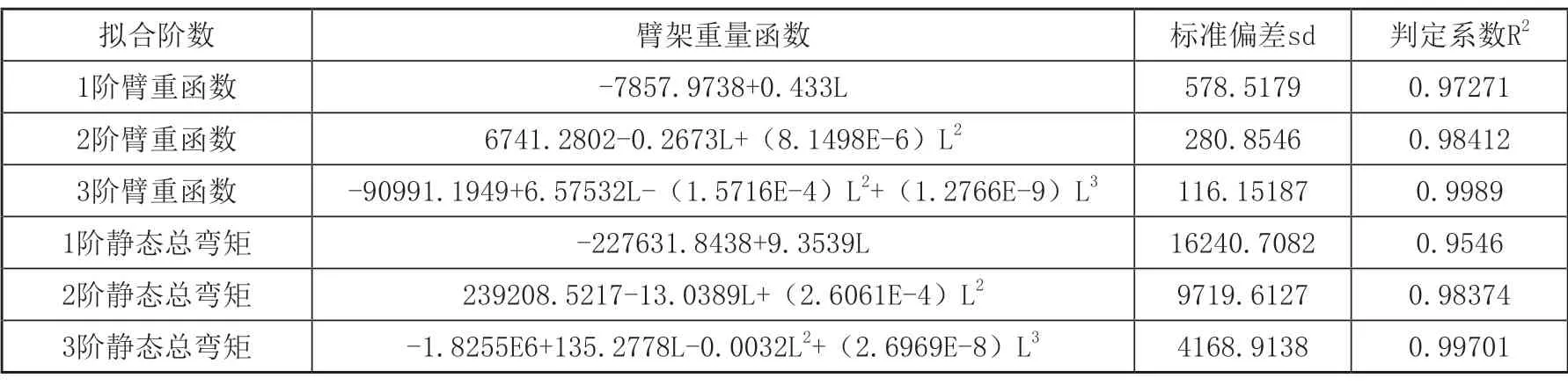
表4 B公司臂架长度与臂架重量、静态总弯矩多项式拟合表

图6 臂长—臂重关系曲线与三阶拟合曲线

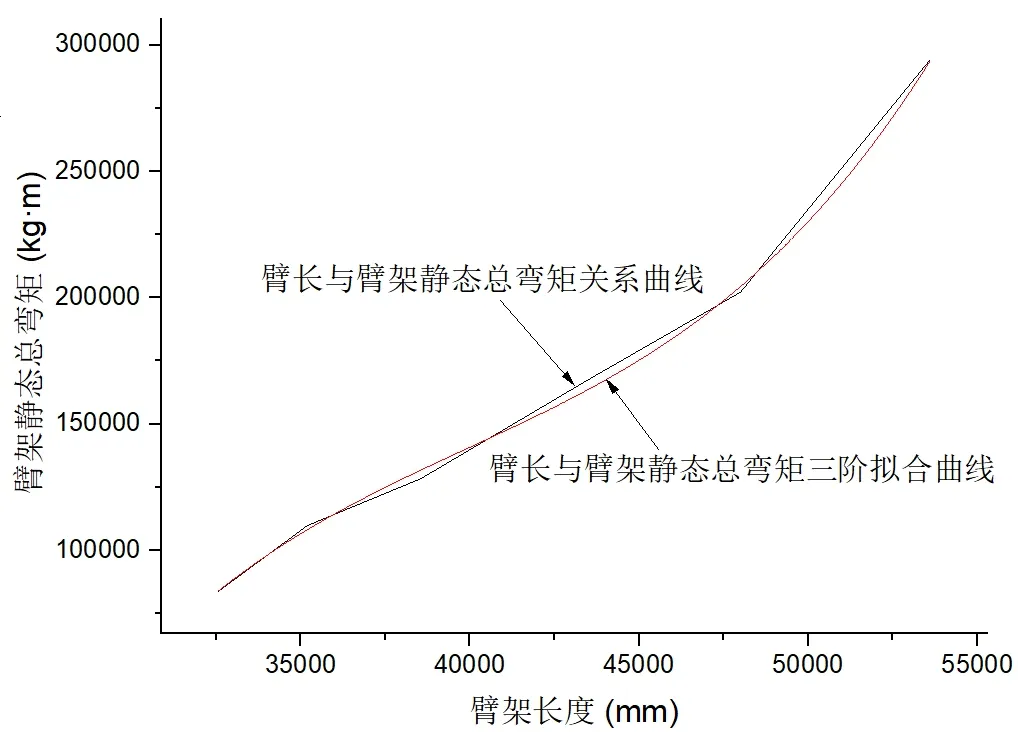
图7 臂长—臂架静态总弯矩关系与三阶拟合曲线

从以上拟合方程和拟合曲线可看出，由于A、B两公司设计理念、臂架结构形式、臂架风格不同，导致两公司臂架系统拟合方程不同，最佳拟合方程的阶数也不同，但臂架系统拟合曲线趋势相同非常接近，标准差、判定系数差别也非常小。

3 实例验证分析

根据市场需求，以开发一款臂架长度45100mm的混凝土泵车新产品为例，使用上述建立的数学模型根据给定的臂架长度分别计算预测A、B两公司臂架重量、臂架长度与臂架静态总弯矩等主要参数，然后与使用精确设计方法得到的臂架系统参数进行对比分析。

3.1 回归分析臂架系统参数

根据A公司二阶臂架系统的臂架重量、臂架静态总弯矩数学模型，使用回归分析可计算出，当臂架长度为45100mm时，臂架重量为12287kg，臂架静态总弯矩为204695kgm。

根据B公司三阶臂架系统的臂架重量、臂架静态总弯矩数学模型，使用回归分析可计算出，当臂架长度为45100mm时，臂架重量为11020kg，臂架静态总弯矩为240667kgm。

从回归分析的计算数据可看出，在臂架长度相同的情况下，B公司臂架结构重量比A公司重量稍轻，但臂架静态总弯矩却比A公司大很多，说明B公司臂架重量主要集中在后面臂节上。从两公司产品的实际使用情况来看，A公司臂架系统的设计理念、臂架结构形式更加适应市场需求。

3.2 臂架系统精确设计参数

臂架系统的精确设计思路是首先在软件中建立臂架的三维模型，使用动力学分析软件建立各相邻臂节之间铰点系统的仿真模型，分析臂架在不同工况下臂节加速度和受力的变化规律，找出臂架计算需要的边界条件和决策依据；然后使用计算软件从末节臂架开始进行有限元分析和结构优化设计，直到计算完所有臂节，确定臂架结构；最后从模型中提取相关数据进行臂架系统主要参数的计算[6～8]。目前，随着对混凝土泵车臂架系统设计计算及优化水平的提高，臂架系统朝轻量化方向发展。本文使用A公司臂架结构形式进行臂架长度为45100mm的完整臂架系统设计，图8～图10所示为臂架系统中1节臂的计算结果，图11是完整的臂架系统三维模型，表5是臂架系统参数表。

图8 1节臂臂架应力变化云图

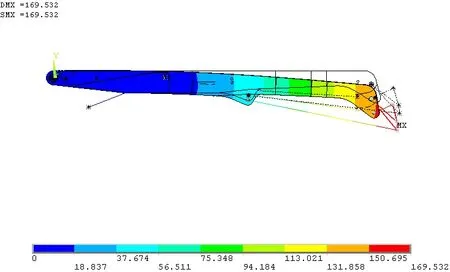
图9 1节臂臂架变形云图

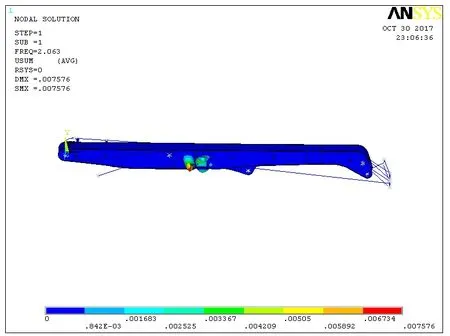
图10 1节臂臂架屈曲模态图

表5 臂架系统精确设计参数表

图11 混凝土泵车臂架系统三维模型

表5 可看出，按照精确设计流程，臂架长度为45100mm时，臂架总重量为12634kg（每节臂架重量已包含其他相关部件重量），臂架静态总弯矩为208520kg·m。数据与A公司回归分析得出的参数非常接近，因此利用回归分析得到的数学模型是可信的。

4 结语

本文利用臂架系统已有的各种数据对臂架长度与臂架重量，臂架长度与臂架静态总弯矩进行多项式回归分析及研究，结果表明：

1）采用多项式回归数学模型拟合混凝土泵车臂架系统中的臂架长度与臂架结构重量，臂架长度与静态总弯矩是可行的、有效的。从标准偏差分析可以看出，利用二项式回归分析建立的数学模型是最优的，也就是说臂架长度与臂架结构重量、臂架长度与静态总弯矩满足二次关系。

2）采用多项式回归数学模型，预测臂架系统主要参数的变化趋势，可以为混凝土泵车新产品的开发提供重要依据，也可以为具有类似臂架结构的高端装备的开发研究提供科学准确参考。