基于PCHIP算法的线圈炮近距离精确打靶设计
刘祚时,程鹏胜*,王梓锐
(1.江西理工大学 机电工程学院,赣州 341000;2.商丘工学院 机械工程学院,商丘 476000)
0 引言
在电磁力被发现以后,世界各国的军事领域都开始对电磁发射开始研究,直到今天电磁力被广泛应用。上世纪70年代初,澳大利亚国防部资助国立大学制造了一台电磁发射装置。1976年Richard Marshall利用新技术将3g重的弹体加速到5.9km/s。这一实验成果证明了利用电磁力把物体推进到超高速的可行性[1]。2008年,美国海军再次试射了优化升级的电磁炮,弹体的出口速度达到了2.3km/s,动能达到10MJ。在5分钟后,弹体以1.7km/s的速度击中了400km外的目标,整个世界为之震惊[2]。2016年5月,利用电磁推进技术制造的超级高铁进行了首次公开测试,并取得成功,其最高运行速度达到600km/h,约为中国高铁速度的两倍[3]。电磁炮的强大杀伤力,和超高的速度使其在军事上更有优越性,目前,电磁发射装置主要有线圈式、导轨式和重接式三种结构[4,5]。在前人研究的基础上,本文对单级线圈炮的定点打靶进行了研究实验,分析了炮筒角度对着弹点位置的影响,并确定了实验系统着弹点的数学模型。
1 线圈式电磁炮的系统设计
本实验设备主要有,云台、线圈、炮筒、stm32单片机、openmv摄像头、mpu6050陀螺仪、步进电机、OLED显示屏等组成。储能电容采用四个串联3300uf-50V的电解电容,每个电容单独充电,每个充电电压是30V,也即通过线圈的电压是120V。炮筒口径为12mm,线圈圈数300匝。系统整体结构如图1所示,实物图如图2所示,图中a为STM32单片机;b为按键模块;c为openmv摄像头;d为步进电机;e为限位开关f为步进电机驱动;g为mpu6050陀螺仪模块;h为OLED显示屏。
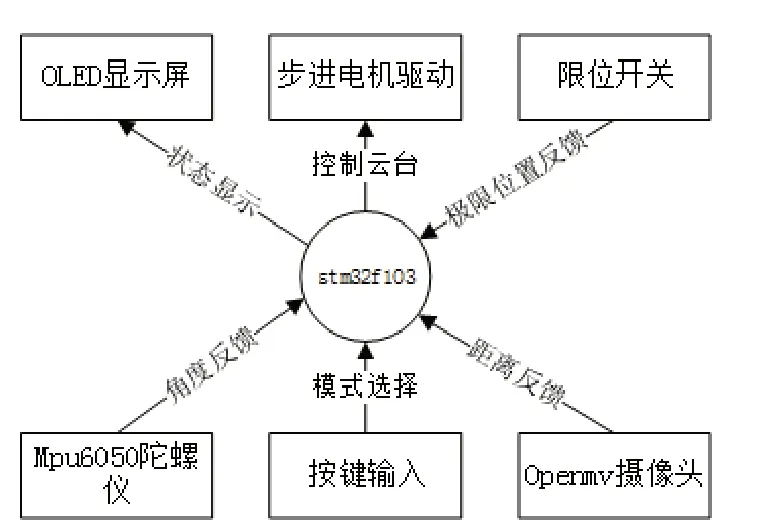
图1 控制系统结构图

图2 电磁线圈炮实物图
系统上电后进行自动校准,云台分别绕z轴和x轴旋转,待触碰到微动开关后标定步进电机每步所转的度数,两个方向全部标定完成后,回归标定后的原点。实验系统分别有手动打靶和自动打靶两种工作模式可通过按键进行选择,在手动模式下,通过按键输入小于等于300cm的距离值,系统开始调整炮筒角度,并进行自动平衡充电,待充电完成后,按发射按钮开炮。在自动工作模式下,由摄像头进行测量距离,测距完成后将距离值发送给stm32单片机,由单片机进行控制步进电机自动调整炮筒角度进行射击。
2 实验系统的搭建
线圈炮线圈采用隔离变压器的初级线圈直径为1.5mm;炮筒采用直径为12mm的PVC管;云台使用PLA材料3D打印成型在水平方向上的减速比为2∶1,垂直方向上的减速比为4∶1。
为保证数据的准确性在着弹点区域放置沙箱,每次钢珠落地都会留下弹坑方便数据记录。沙箱如图3所示。

图3 沙箱
3 自动校准功能的实现
在实验过程中,通过步进电机来进行角度的精确调整,由于步进电机并没有中位,不能保证每次开机步进电机都在同一位置,故加入了自动校准功能。自动校准的实现方式为在控制炮筒水平运动和俯仰运动的路径上,且在工作行程之外加入两个微动开关。在微动开关被触发后由stm32单片机记录极限位置并标定步进电机的转动度数,最后控制两路步进电机回到标定后的原点。自动校准流程图如图4所示。

图4 自动校准流程图
4 建立PCHIP数学模型
4.1 原始实验数据的获取
由于在电磁炮的发射实验中影响因素较多,为获得较为准确的实验数据,其中主要影响因素有分别为:发射电压,电容容量,装弹位置和炮筒角度。通过单一变量法,逐个确定了各影响因素的值:电容电压120V;容量3300uf;装弹位置距离炮筒末端1cm的位置;炮筒角度为30°时钢珠打到300cm的位置。比较准确的数学关系,分别测试了分段三次Hermite插值和拉格朗日插值拟合效果。
4.2 分段三次Hermite插值原理
在节点xk(k=0,1,...,n)上通过导数值f'k=mk(k=0,1,...,n),构造一个导数连续的分段插值函数Ih(x),根据两点三次插值多项式,Ih(x)在区间[xk,xk+1]上的表达式如式(1)所示[8]。
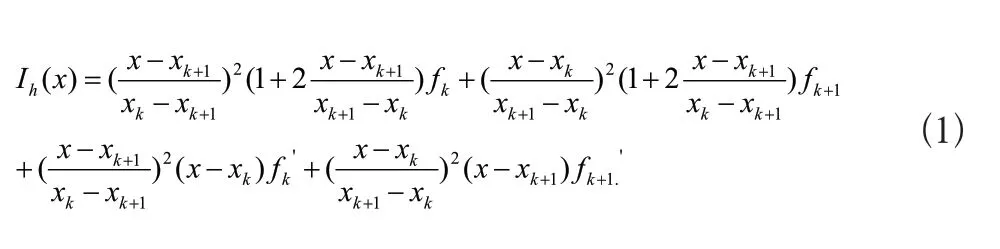
在MATLAB上进行多种插值算法的拟合运算,不同算法得拟合曲线如图5所示。
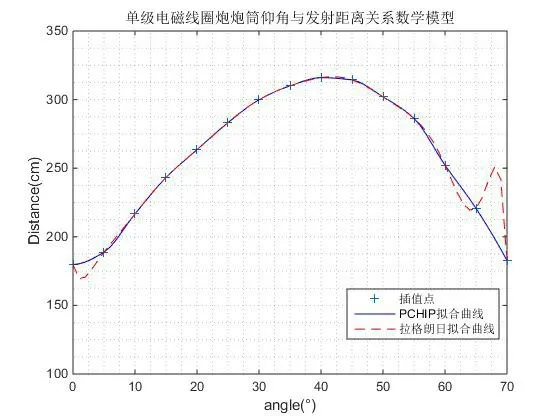
图5 两种插值算法的对比
由图可知,PCHIP方式插值方式得到的曲线与原始数据的拟合程度更高,而拉格朗日插值算法仅在角度为5°到55°的效果明显,在起始端和结束端误差较大为取得与原数据更好的拟合效果故选择PCHIP插值方式。通过计算所得曲线表达式如式(2)所示。
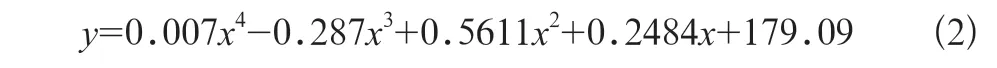
其中x为炮筒角度,y为钢珠发射距离。
利用三次Hermite插值多项式的余项计算误差,如式(3)所示。
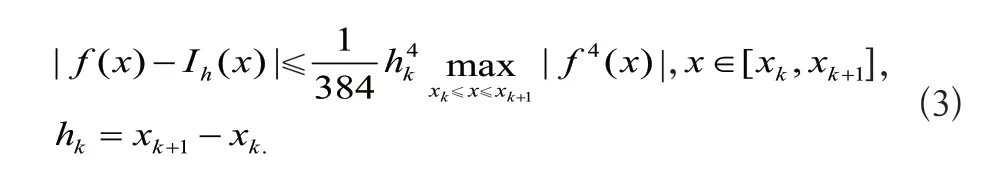
由实验数据是完全等距的,将已知数据代入误差计算公式,误差为1.63cm。曲线的拟合误差在2cm以内,远小于要求的50cm,故不影响实验的准确性。
5 实验结果分析
对电路进行检查,确认无误后,将拟合后的每一度所对应的距离值录入单片机程序中。靶环水平放置在地面上(每环间距5cm),在靶环的后方一定距离有竖直放置的标识,通过Openmv摄像头进行测距,以便获得当前靶心位置。选取5个点进行测试,为获得较准确的数据,在每个角度下测试5组取其平均值。结果如表1所示。

表1 理论值与实际值对比表
由表可知,在角度为10°和30°的时候偏差较小,而整体的误差在厘米级甚至更小,误差产生的的原因可能时,电容在多次充放电后,容量有些改变,但是与拟合结果基本相同,说明插值方法有效。
6 结语
通过单一变量法获得最佳的发射效果,在对不同角度下的钢珠射出的距离进行多次实验后,通过MATLAB进行插值运算,与原始数据进行曲线拟合,最后将插值所得到数据录入到stm32单片机程序中进行实验验证。分析实验结果,误差仅在小范围内波动,对靶环能实现精准打击。对实现电磁线圈炮近距离确定着弹点位置的研究有重要参考意义。

