硅锭电火花线切割RBF-PID恒张力控制研究
刘鹏,罗福源,孙凌云
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
硅晶体材料硬度高、脆性大,一般的机加工方法容易产生崩裂,或者由于解理现象产生整体断裂,可加工性极差[1]。高速往复电火花线切割(WEDM)因其非接触加工方式正逐渐成为硅晶体的有效加工手段[2]。但是在切割加工过程中电极丝由于受到诸多外界因素干扰,会产生位置偏移,且偏移量会随着张力的变化而改变[3],这严重影响硅片表面切割质量与加工的稳定性。
为解决电极丝张力波动带来的诸多问题,众多学者在控制张力波动方面进行了深入研究和探索。程伟建[4]采用“重锤加双导轮钼丝松紧调节器”组合的方式对电极丝张力进行控制,在一定程度上解决了电极丝振动幅度大的问题;蒋近等[5]采用基于相邻轴误差的多电机同步控制方法,保证了切割线张力稳定。李强[6]采用带死区的PID对电极丝张力进行闭环控制。HAAS P等[7]对切缝中的流场进行仿真分析,设计了可以高效清洁电解物的新型喷嘴,有效降低了冲洗过程对电极丝的影响。这些学者都在机械结构方面作出了一定改进,并以此为基础采用较为传统的控制方法对张力进行控制。但张力控制系统实际上是一个复杂的机电控制系统,系统的参数随着加工的进行往往会发生变化,采用传统的控制方法难以进一步突破提高张力控制精度的瓶颈。本文针对硅锭加工过程中电极丝张力波动的问题,设计了恒张力控制系统,并以此为基础,采用RBF神经网络对PID参数进行自动快速整定,克服了PID手动调参速度慢、不准确以及系统参数改变后需再次整定的缺陷,使电极丝张力在整个硅锭切割过程中保持良好的稳定性。
1 恒张力控制系统工作原理
电火花线切割恒张力控制系统根据执行机构的不同可以分为机械式、磁粉式和电机式。机械式存在控制精度低、时滞性大等缺点。磁粉式虽具有张力调节方便、快捷等优点,但对张力的恒定起效慢[8],难以满足硅锭切割过程中对张力伺服执行装置的快速响应性等要求。另外,传统的非对称式恒张力控制方案在往复走丝电火花线切割机床中存在加工区域电极丝张力不一致的固有缺陷。因此本文基于电机式的执行装置设计了如图1所示的双边恒张力控制系统。

图1 恒张力控制系统原理图
储丝筒电机在正常运转前,通过PC上位机设置电极丝目标张力值,张力传感器在控制系统中作为反馈元件,负责采集电极丝的实际张力值,将采集到的张力值转化为数字量信号后送入控制器,控制器根据设定目标值与实际值的差值来控制伺服执行装置的速度以及方向,直流伺服驱动装置将伺服电机的旋转运动转化为直线运动以控制丝架上电极丝的长度,从而达到控制电极丝张力的目的。
2 控制对象模型构建
将电极丝恒张力控制过程简化成如图2所示。
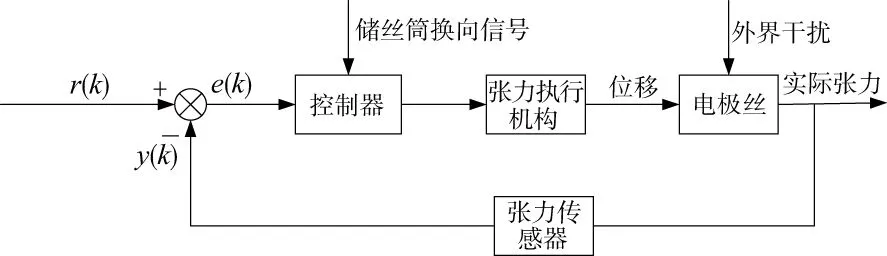
图2 恒张力系统控制框图
张力执行环节由直流伺服电机以及直线滑台组成,直线滑台将直流伺服电机的旋转运动转化为滑台的直线运动,电机通过联轴器与丝杆相连,丝杆带动张力调节轮上下运动,从而驱动电极丝长度改变,进行张力实时调整,伺服执行机构系统框图如图3所示。

图3 伺服执行机构系统框图
伺服执行机构的传递函数为
(1)
电极丝作为最终被控对象,输入为位移,输出为电极丝的实际张力,在电极丝弹性形变范围内,可将这一部分传递函数表示为
(2)
由此可以得出被控对象的系统传递函数为
(3)
式(3)中参数含义及其所对应的数值如表1所示。
汤翠坚持了四天,终于崩溃。她告诉警察,不用检测,白骨应该是汤莲的。那天在工地上她就通知了丈夫侯大同,说铲掘机在他们家的无花果树下挖出一堆白骨。她回来,侯大同不见了。
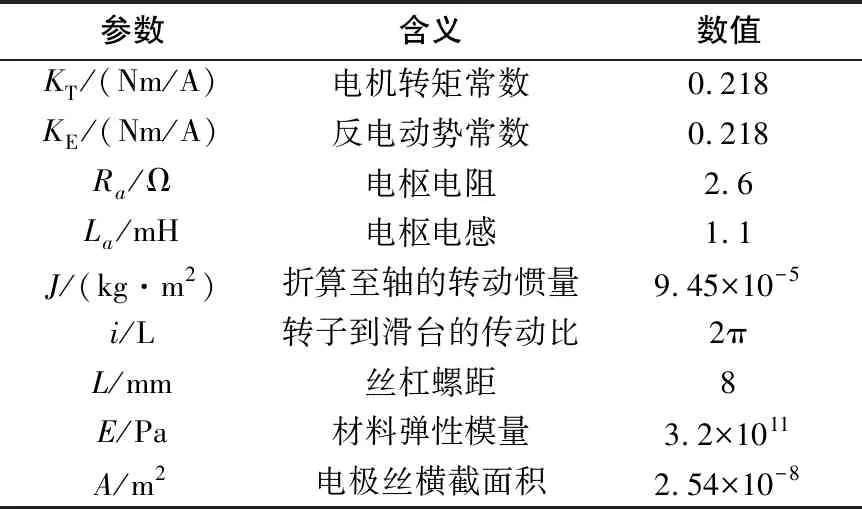
表1 传递函数中相关参数的数值及其含义
3 RBF-PID张力控制器设计
RBF神经网络是一种三层向前的局部逼近网络,由于输入到输出的映射是非线性的,而隐含层空间到输出空间的映射是线性的。因此能够加快学习速度并避免局部极小问题[9-10],其结构如图4所示[11]。

图4 RBF神经网络结构
假设径向基(RBF)神经网络中输入层节点的个数为n,则可用向量表示为
X=[x1,x2,x3,…,xn]T
(4)
输入层到隐含层的权值为1,隐含层节点个数为m,设RBF神经网络的径向基向量为H=[h1,h2,h3,…,hm]T,选取高斯函数作为径向基函数,则hj可以表示为
(5)
式中:bj为隐含层第j个神经元节点的基宽参数;Cj=[cj1,cj2,cj3,…,cjn]T为隐含层第j个神经元的中心向量。设隐含层到输出层的权值向量为W=[w1,w2,w3,…,wm]T,则输出层可以表示为
Y=WT×H
(6)
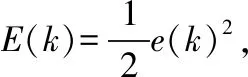
(7)
(8)
(9)
考虑上次权值调整量大小对本次权值调整的影响,引入与上次调整有关的动量系数β,动量系数取值在0~1之间,以平滑权值等参数调整过程,避免引起调节震荡,进行第k次更新得到第k+1次网络参数为:
wj(k+1)=wj(k)+ηΔwj(k)+βΔwj(k-1)
(10)
bj(k+1)=bj(k)+ηΔbj(k)+βΔbj(k-1)
(11)
cji(k+1)=cji(k)+ηΔcji(k)+βΔcji(k-1)
(12)
将本文电极丝张力伺服控制系统引入径向基(RBF)神经网络加经典的增量式PID控制,得到图5所示的基于RBF神经网络的PID恒张力控制器。
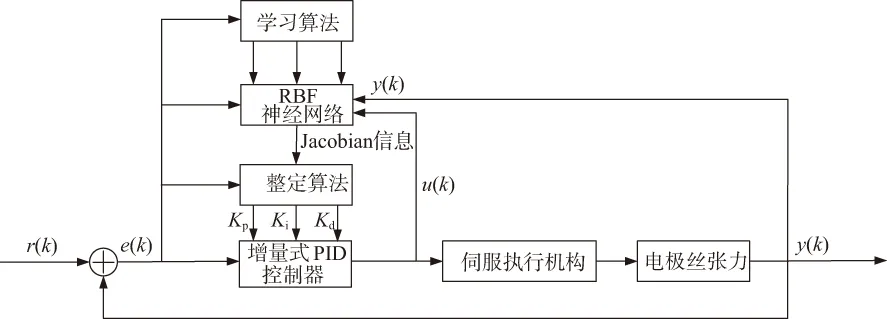
图5 RBF-PID恒张力控制器
额定电极丝张力输入信号r(k),与经过传感器测得的实际输出信号y(k)相比,得到偏差信号e(k)、u(k)以及y(k)作为RBF神经网络的输入信号,经过RBF神经网络整定后得到PID控制器的3个参数Kp、Ki、Kd。取PID参数向量K=[Kp,Ki,Kd]T,采用梯度下降法对PID 3个参数进行调整,调整公式如下:
(13)
(14)
(15)

(16)
4 仿真与实验分析
4.1 Matlab仿真
本文采用Matlab自带的Simulink工具箱结合S函数对两种不同的控制算法进行仿真。首先取神经网络的结构为3-6-1,并确定RBF网络输入为e(k)、u(k)、y(k)。然后构建被控对象数学模型,并将被控对象离散化处理,取采样周期为10 μs。最后给定阶跃输入信号,搭建的Simulink仿真系统框图如图6所示。
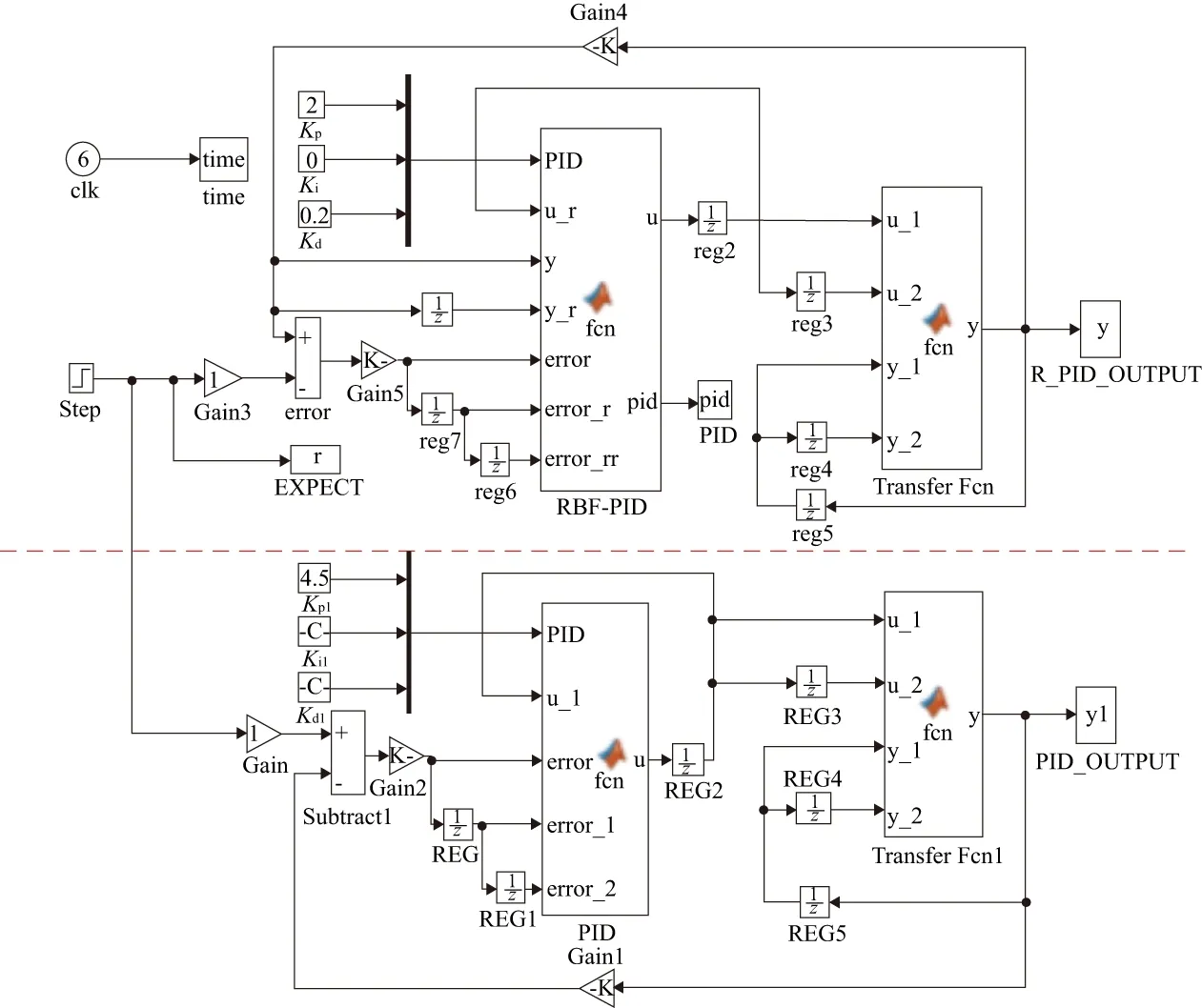
图6 Simulink仿真系统框图
利用试凑法不断完善普通PID的3个控制参数,得到Kp=4.5、Ki=0.35、Kd=0.1。与RBF-PID仿真对比,效果如图7所示。
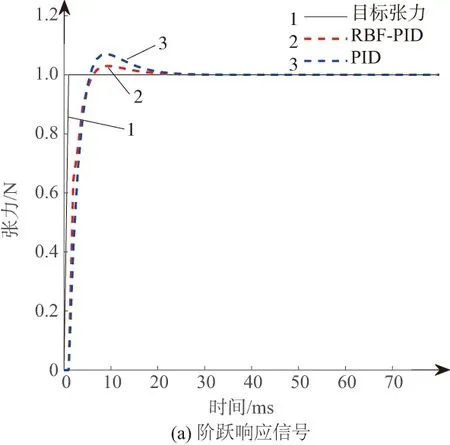
图7 仿真系统输出
图7(a)中线1代表期望输出,线3是通过试凑法得到的PID仿真波形,线2为基于RBF的PID仿真波形。图7(b)中线1为基于RBF的PID输出误差跟随曲线,线2为普通PID误差跟随曲线。分析图7(a)可知,采用RBF-PID控制方式下输出信号的超调量略低于普通PID控制方式,控制系统稳定的时间基本都在25 ms附近,两者控制效果基本一致,均满足控制系统精度及其稳定性要求。
随着加工进行,系统参数会发生变化,当电极丝的直径由原来的0.18 mm磨损至0.15 mm时,电极丝横截面积变为1.77×10-8m2,此时普通PID若用原来的PID参数,即会出现张力控制系统超调量大、调整时间长等现象,严重的还会引起系统振荡,如图8所示。普通的PID的超调量已达20%左右,系统稳定的时间也增加了1倍左右,控制效果已满足不了张力控制的高精度、快速调节的要求;采用基于RBF神经网络的PID控制可以根据系统自动优化PID参数,输出响应的超调量在5%以内,在25 ms内完成对目标值追踪,解决了系统参数变化后普通PID控制效果变差的问题,提高了系统的稳定性。

图8 系统参数变化后仿真系统输出
RBF神经网络可根据系统的参数完成PID参数的快速调节,系统参数变化之后RBF调节PID参数曲线如图9所示。
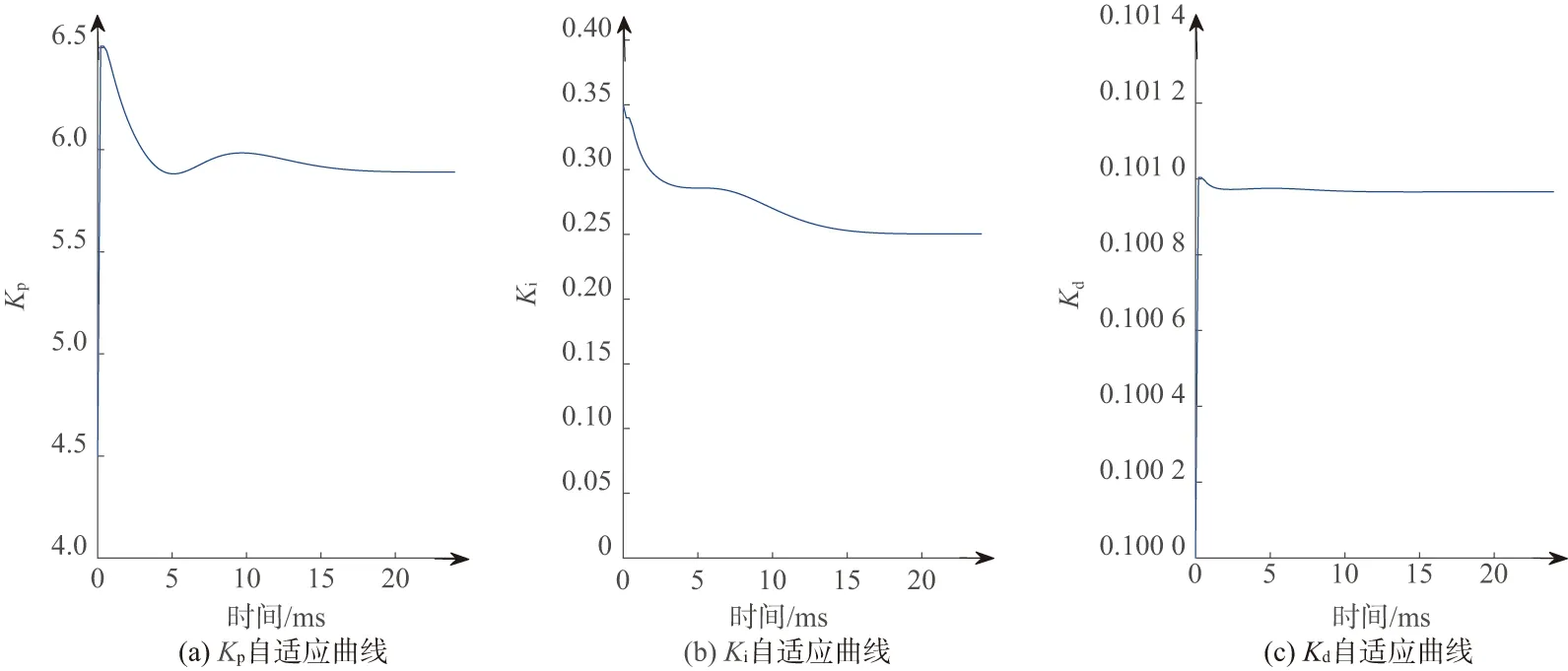
图9 PID参数整定曲线
优化后的RBF-PID算法根据系统参数不同完成了PID参数的自适应调节,调节的时间控制在15 ms以内,满足控制系统调节的快速性需求,克服了系统因参数发生变化需手动试凑PID参数的缺陷,进一步提高了系统的自适应性与抗干扰性。
4.2 张力波动实验分析
搭建如图10所示的实验样机进行张力波动控制实验,此样机可以完成弹簧式、普通PID、RBF-PID 3种不同的控制方式下张力控制实验。其中,机床上的紧丝器用以完成弹簧式恒张力控制,伺服执行机构结合控制器、上位机软件完成其他两种控制方式。FPGA实现传统PID控制,上位机软件实现张力数据实时显示以及RBF神经网络优化部分,更新后的PID参数通过千兆以太网传输至PID控制器。

图10 恒张力控制实验样机
实验时采集20 s内电极丝张力的平均值、最大值和最小值,并计算张力的波动率。张力波动率公式如下:
(17)
采用弹簧式恒张力控制装置走丝速度10 m/s时张力波动率高达18.63%,如图11所示。在普通PID控制方式下,张力波动率随丝速的上升较为缓慢,对电极丝张力值有较好的控制作用。采用基于RBF神经网络的PID控制方式,张力波动率几乎不会随着丝速的上升而增加,可以很好地将张力波动率控制在5%以内。此外在丝速相同的情况下,基于RBF神经网络的PID控制张力波动率最小,对电极丝张力控制效果最为显著。
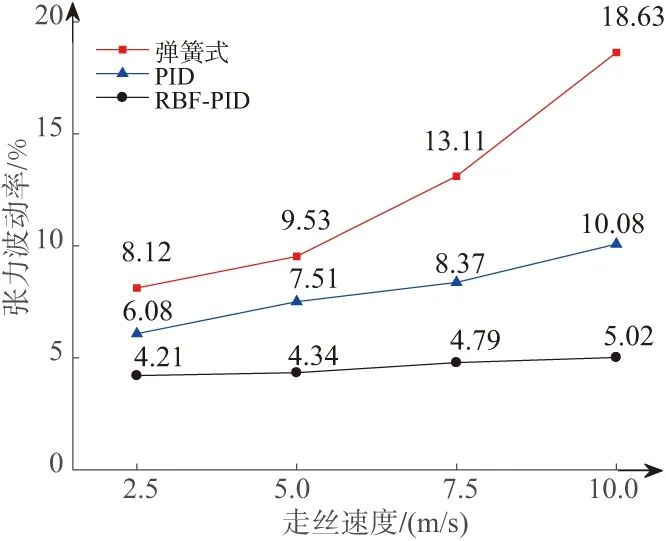
图11 张力波动率随速度变化曲线
提高预紧力有利于降低电极丝张力波动率,并提高硅片表面切割质量,但过大的预紧力会增大电极丝磨损速度,降低电极丝使用寿命。本文优化后的控制算法便很好地解决了此矛盾点。图12表示的是在走丝丝速7.5 m/s下,张力波动率随预紧力的变化规律。当电极丝的预紧力下降时,采用弹簧式恒张力控制方式会使张力波动率迅速上升,此时若要进一步降低张力波动率,须提高电极丝预紧力,不可避免地降低了电极丝使用寿命;使用普通PID控制方式时,张力波动率得到了较好的控制,预紧力对张力的影响效果也有所降低,但整体效果要劣于优化后的PID算法。在同一预紧力下,优化后的PID控制张力波动率最低,抑制了电极丝高预紧力的影响,进一步提高了电极丝使用寿命。
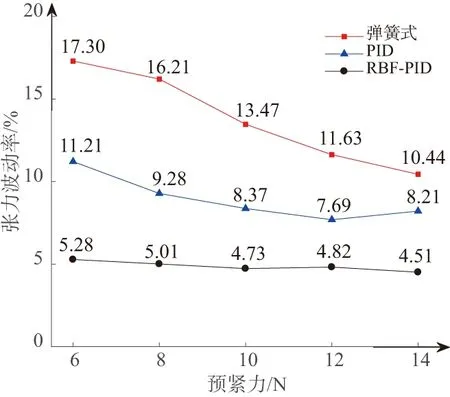
图12 张力波动率随预紧力变化曲线
在张力波动率方面,优化后的PID控制算法较普通PID算法平均降低了40%,将波动率控制在5%以下,满足硅锭切割对电极丝张力的苛刻需求,同时使用优化后的算法可以在适中的电极丝张力、较高的丝速下工作,在保证硅片加工质量的前提下,更好地提高电极丝的使用寿命与加工效率。
5 结语
1)张力控制系统是一个复杂的机电控制系统,系统参数随加工过程往往发生变化,传统的PID控制算法需要根据系统手动更新参数,难以保证张力控制的精度与稳定性要求。
2)仿真结果表明,RBF神经网络可根据系统参数实现PID控制参数自动、快速优化,解决了PID手动调参速度慢、不准确以及系统参数改变后需再次整定的一系列问题。进一步提高了张力控制系统的响应速度与控制精度。
3)实验结果表明,采用RBF-PID控制算法的控制器可将张力波动率控制在5%以内,比普通PID降低了40%,显著地抑制了电极丝磨损变形以及走丝速度、预紧力变化等对张力稳定性的影响。

