基于自适应阻抗模型的双机器人协调搬运内力控制

王耀武，张得礼，胡雪刚

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

双机器人运动学协调分为相对协调和同步协调[1]。在相对协调任务中，双机器人末端工具的相对位姿发生变化，比如双机器人协调完成工件的喷涂任务；在同步协调任务中，双机器人末端工具的相对位姿不发生变化，比如双机器人协调搬运。在同步协调任务中，典型的如搬运，由于机器人自身的定位精度误差、双机器人之间坐标系标定的误差、工件的尺寸误差等，若双机器人是在位置控制模式下进行任务，则不可避免地会对物体施加很大的内力，严重时会对物体和机器人造成损坏[2]。因此需要对物体上的内力进行控制。

目前双机器人协调内力控制方法主要如下：文献[2]针对双机器人搬运作业中的内力控制问题，提出基于遗传算法的阻尼比例微分控制方法，但是参数调整和择优过程繁琐。文献[3]采用变阻抗模型对两个机器人对物体施加的力进行调整，同时克服外界的扰动力实现机器人对外界的柔顺。文献[4]基于双机器人对等架构采用阻抗控制同时调整双机器人和物体之间的接触力。文献[5]采用位置/力混合控制，同时控制两个机器人和物体之间的接触力。上述研究都是同时调整两个机器人对物体的接触力，可能会产生新的内力，而且文献[5]中位置力/混合控制不适用大部分只开放位置控制权限的机器人。文献[6]通过模型参考自适应算法来调整从机器人的运动轨迹进而控制内力，但是模型数学运算不利于实现。文献[7]提出了面向被操作对象的协调策略，并对作用于被操作对象的合力进行力分解。文献[8]在此基础上提出了面向被操作对象的内外阻抗控制策略。虽然上述研究考虑了双臂对物体的内力和外力控制，但是都采用定阻抗的控制策略，鲁棒性不强。除此之外，其他的智能控制策略如文献[9-10]也用到了协调控制中，这种模型有过于复杂、强耦合、非线性等缺点，并未在现有的控制系统中得以应用。

针对上述双机器人协调内力控制方法存在的问题，本文在双机器人主从协调架构和所介绍的内力计算模型的基础上，提出了基于自适应阻抗模型的从机器人单端位置调节内力控制策略。由于双机器人作用于物体上的内力是一对相互作用力，在搬运过程中，规划的主机器人的离线轨迹不变，从机器人根据其对物体的内力大小来调整自己的位置。基于上述策略有效地解决了双机器人协调搬运过程中的内力控制问题。

1 运动学分析和内力建模

如图1所示，Tw表示双机器人系统的世界坐标系；Tb1表示主机器人的基坐标系，Tw和Tb1重合；Tb2表示从机器人的基坐标系；Te1表示主机器人和物体接触点处的坐标系，Te2表示从机器人和物体接触点处的坐标系；o表示物体的质心；To表示物体质心处的坐标系；b1Te1表示Te1相对Tb1的表达，b2Te2表示Te2相对Tb2的表达；b1Tb2表示Tb2相对Tb1的表达；e2Te1表示Te1相对Te2的表达；l1表示主机器人和物体的接触点到物体质心的矢量，l2表示从机器人和物体的接触点到物体质心的矢量；Fe1、Ne1表示主机器人在接触点处对物体施加的力在Te1中的表达；Fe2、Ne2表示从机器人在接触点处对物体施加的力在Te2中的表达；Fo1、No1表示主机器人在接触点处对物体施加的力在To中的表达；Fo2、No2表示从机器人在接触点处对物体施加的力在To中的表达。

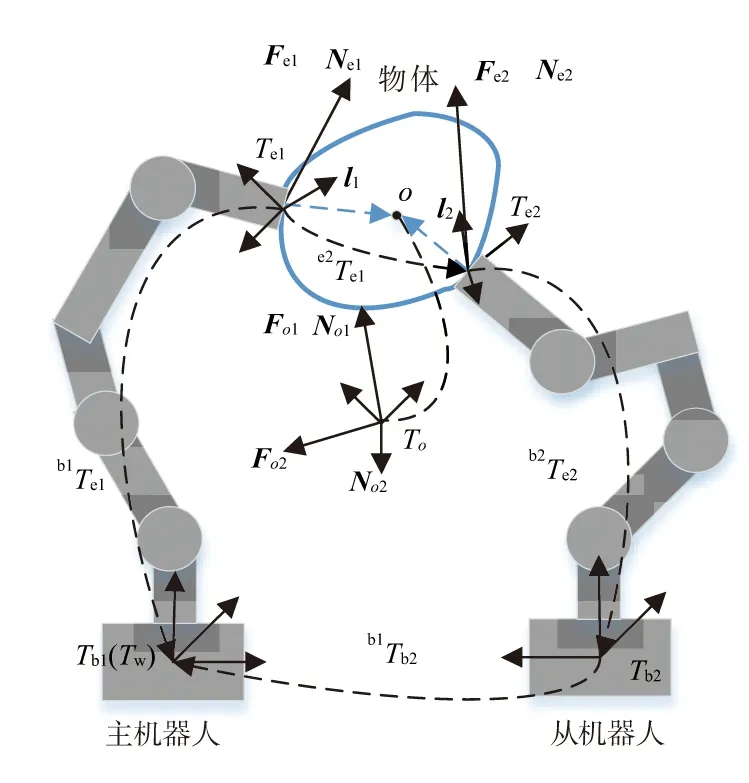
图1 双机器人协调运动学和静力学关系

由图1中双机器人主从协调搬运的运动学闭环链[11],可得公式(1)。由公式(1)可知，只要知道b1Tb2、b1Te1、e2Te1，就可以知道b2Te2，即主从协调是从机器人跟随主机器人的运动而运动。

b2Te2=(b1Tb2)-1b1Te1(e2Te1)-1

(1)

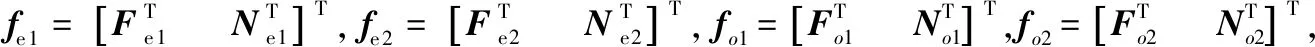
(2)

(3)

式中：oRe1表示Te1相对于To的旋转矩阵；S(l1)表示对l1的叉乘运算，其结果为3×3的矩阵；oRe2表示Te2相对于To的旋转矩阵；S(l2)表示对l2的叉乘运算，其结果为3×3 的矩阵。物体所受的内力[12]如公式(4)所示。

(4)

式中：fi表示物体所受的内力，其是一个12维的矢量；fi1表示主机器人对物体的内力，fi2表示从机器人对物体的内力，都是6维的矢量。fi1和fi2是一对相互作用力，它们都是相对于To的。

2 内力控制策略

2.1 自适应阻抗模型

以某一维度力控制为例，自适应阻抗模型[13]的公式表达式如式(5)所示。

(5)

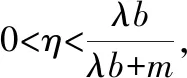
自适应阻抗模型的控制框图如图2所示，除相关字符含义上已说明外，Ke表示环境刚度，x表示机器人实际跟踪到的位置，一般认为xc=x。

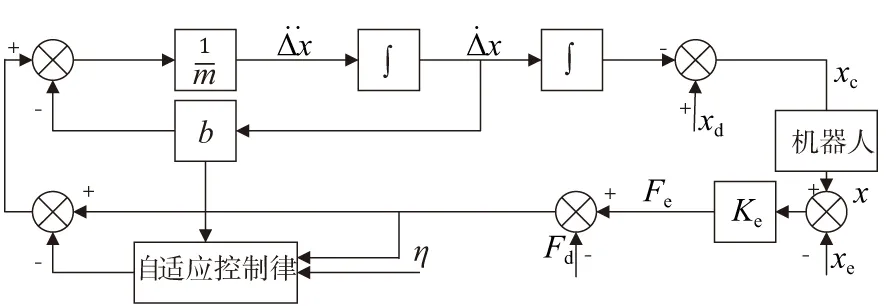
图2 自适应阻抗阻抗模型控制框图

2.2 从机器人单端调节内力控制策略

内力控制策略如图3所示。xd1表示主机器人规划的期望轨迹，xd2表示从机器人规划的期望轨迹；x1表示主机器人的实际轨迹，x2表示从机器人的实际轨迹；xc2表示修改后的从机器人的实际轨迹；Fe1表示主机器人和物体的接触力，Fe2表示从机器人和物体的接触力；oFi2表示从机器人对物体的内力在物体质心坐标系To中的表达；oΔx2表示从机器人的位置修正量在To中的表达，Δx2表示oΔx2经坐标系变换到从机器人末端的位置修正量；oFd表示从机器人对物体的期望内力在物体质心坐标系To中的表达。

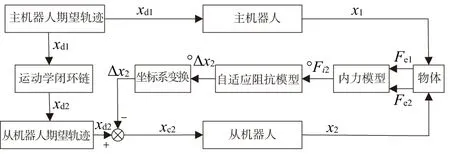
图3 内力控制策略框图

由上文内力模型可知，双机器人作用于物体的内力是一对相互作用力，因此，控制一个机器人对物体的作用力即可。在双机器人搬运过程中，根据双机器人对物体的接触力可实时计算出从机器人对物体的内力，根据期望内力oFd和上文的自适应阻抗模型可实时计算出从机器人的位置修正量Δx2来实时修改从机器人的期望轨迹,从而使控制内力控制在期望水平上。

3 仿真和实验

3.1 仿真和实验模型的建立

如图4所示，双机器人末端安装有法兰，从机器人法兰安装力传感器，所搬运物体为铝质薄壁箱体，长、宽、高分别为280 mm、220 mm、120 mm。在箱体长度方向人为加入环境阻抗，即厚度都为10 mm的橡胶垫，橡胶垫和箱体总质量约为2.1 kg，双机器人通过和橡胶垫接触产生一定压力来完成搬运任务。箱体质地均匀，To取在箱体几何中心，Tb1、Tb2之间的位姿关系由四点握手标定法[14]得到，传感器坐标系(图中未标出)的z轴和Te2的z轴共线。

图4 双机器人协调搬运示意图

图4是搬运前的初始状态，双机器人到达指定位置和橡胶垫接触产生期望内力oFd和-oFd，To、Te1、Te2各坐标轴平行。启动搬运后，Te1的x、y、z轴和Tb1的z、y、x轴保持平行，只有相对位置发生变化。主机器人先在Tb1的z轴正向移动40 mm，然后在Tb1的y轴移动400 mm，最后在Tb1的z轴负向移动40 mm，速度为20 mm/s。整个搬运过程从机器人进行跟随运动，即双机器人搬运箱体完成抬起、移动、放下的搬运任务。

分析图4，由上文介绍的内力计算模型可以知道，从机器人对物体的内力就是传感器z轴检测到的力的反力，oFd和-oFd就是物体z轴受到的内力(压力)，控制过程就是根据oFd和搬运过程产生的内力经过自适应阻抗模型产生从机器人末端的位置修正量，从机器人不断修正位置从而把内力控制在oFd。

3.2 仿真验证

经多次橡胶垫挤压实验，测定橡胶垫和机器人之间的接触刚度约为50 N/mm。根据箱体和橡胶垫质量以及机器人和橡胶垫之间的摩擦系数初步估计搬运箱体所需最小期望内力oFd=50 N，这个内力是使物体在搬运过程中不掉落的最小内力。为了模拟实际搬运过程中从机器人末端在z轴方向相对于主机器人末端的位置变化，给从机器人末端一周期为搬运总时间，即24 s、幅值为0.5 mm的位置误差信号。在Matlab/Simulink中搭建仿真模型，通过仿真得到结果。

如图5所示，未进行力控制之前，双机器人对物体的压力，即内力，在25 N～75 N之间变化，开启内力控制之后，通过调整公式(5)中的阻抗参数和更新率，内力被稳定控制在(50±0.5)N。

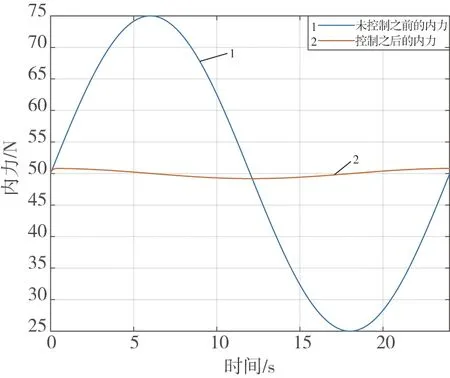
图5 内力控制仿真结果

3.3 实验验证

根据3.1节介绍的仿真模型搭建实验平台，如图6所示。实验使用的机器人是埃斯顿六关节通用机器人ER30和ER20，分别作为主机器人和从机器人，传感器使用某公司的M3714A搭配M8128B1采集盒。传感器安装在从机器人末端，采集到的数据经采集盒处理后上传到上位机，供编程处理使用。这里需说明，所有的轨迹规划程序都是作者在上位机上编程实现，用到的只是机器人控制器的伺服功能，上位机和机器人控制器的通信周期为10 ms。

图6 双机器人协调搬运实验

经过多次运动实验，确定oFd=60 N，此内力刚好可以完成搬运任务且不会产生多余的内力。为了编写力控制程序，公式(5)经过后向差分离散化[15-16]之后在上位机上编程实现，通过多次调整公式(5)中的阻抗参数和更新率，得到最终的实验结果。

图7所示是传感器采集到的控制前后的内力变化曲线。在进行内力控制之前，只进行运动控制完成搬运轨迹，搬运总时长24 s，其中抬起2 s，放下2 s，移动20 s。在抬起和移动、移动和放下的转折点处由于相对位置误差突然变大导致内力发生突变，搬运过程中内力最大为120 N。由于接触刚度为50 N/mm，双机器人间最大约有1.2 mm的相对位置误差。在开启内力控制之后，不仅在转折点处把内力及时控制在60 N左右，在移动过程中内力也被稳定控制在(60±2)N。

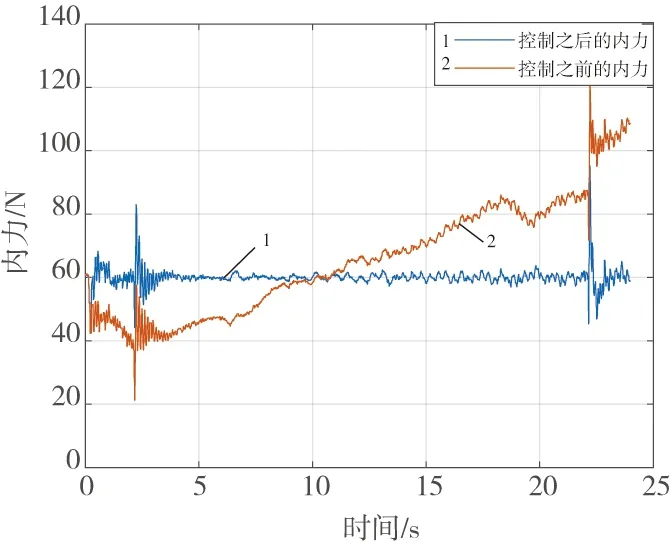
图7 内力控制实验结果

4 结语

本文所提出的基于自适应阻抗模型的从机器人单端位置调节内力控制策略有良好的效果，在双机器人搬运箱体完成抬起、搬运、放下且速度为20 mm/s的运动轨迹过程中，给定物体z轴期望内力60 N的任务要求，最终内力不仅在移动过程中被控制在(60±2)N，在抬起和移动以及移动和放下的转折点处，物体内力有突变的情况下，仍然被及时地控制在期望水平。