拓扑近藤绝缘体SmB6中的奇异电子性质

赵 淦，张明远，王佳敏，张 旺，苗 霖

1.东南大学物理学院,南京市东南大学路2号,南京211189

目 录

I.引言

拓扑物相是现代物理学的一个重要新概念，它衍生出了包括拓扑绝缘体，外尔半金属等众多具有奇特量子基态或激发性质的电子材料[1–3]。拓扑物相的发现不只在凝聚态物理中开拓了新的视界，更深层次地连结了凝聚态物理和其他物理学分支，如光学和高能物理学等。而将受对称性保护的非平庸拓扑序同关联电子体系融合而成的关联拓扑电子体系，促使了人们在凝聚态体系中探索和发现新的量子现象，比如马约拉纳零能激发[1]和轴子电动力学[1,4,5]等。

自从2010年起，Maxim Dzero等人第一次提出了Topological Kondo Insulator，即拓扑近藤绝缘体的概念[6]。他们论证了在传统的关联电子体系 近藤绝缘体中可能存在非平庸的拓扑物相，从而属于Z2类的拓扑绝缘体。并且给出了六硼化钐(SmB6)可能是这样一个关联性的拓扑电子材料的预测。在随后的近10年中，随着拓扑材料研究的愈发深入，拓扑近藤绝缘体的理论工作被不断地完善。然而，作为第一种被预测为拓扑近藤绝缘体的SmB6在这10年中反复地被多种实验手段研究，经历了多次的争议和疑问，SmB6才最终被凝聚态物理学界广泛接受为第一个拓扑近藤材料。即便到了今天，SmB6作为一个拓扑近藤绝缘体，它本身仍有众多的未解之谜。作为这种传奇材料探索研究的见证者和经历者，我们认为对于SmB6中新奇物理现象的理解传播给读者是很有价值的，这也是写作本文的初衷。

在下文中，我们将分成几个部分对SmB6中的奇异电子性质进行介绍。第二部分，我们主要介绍SmB6的拓扑近藤绝缘体的物理理论模型。该部分主要介绍对SmB6的拓扑归类的研究，以及利用第一性原理计算对SmB6的基态电子结构的描述，从理论上得到SmB6作为拓扑近藤绝缘体的基本物理图像。

第三部分，我们主要介绍了SmB6的电输运性质。SmB6之所以被人们推测可能具有拓扑表面电子态，一个重要的原因是它独特的输运性质。SmB6在极低温下的电阻出现了饱和现象，并且其起源不是来自于杂质或者缺陷态。许多研究团队设计出了多种电输运的测量方法，从而证明了SmB6的低温电阻饱和平台具有二维性质，且只会对磁性杂质敏感，其起源可能就是SmB6的拓扑表面电子态。

第四部分，我们集中介绍对SmB6的角分辨光电子能谱研究(ARPES)，这是本篇综述着墨较多的部分。ARPES技术手段在拓扑材料研究中大放异彩，其关键之处在于电子结构的拓扑非平庸序的一个重要可观测效应是界面的低维电子态，这恰好就是ARPES手段的强项。然而在这部分介绍中，我们会发现，ARPES在解析SmB6的电子结构时，由于SmB6本征的微小能隙和能量分辨率受限等缘故，SmB6的ARPES结果通常都伴随着正反两面不同的解读声音。随着包括自旋分辨的ARPES积累和来自不同晶面包括(001)面和(111)面的数据对比，人们才逐渐了解SmB6的表面电子结构。在该部分中，笔者融合了部分由我们小组参与的SmB6中的磁性掺杂效应研究。研究发现，过量的磁性掺杂并不会破坏SmB6中的Z2保护的表面电子态，并对多种可能的物理原因进行了分析。

第五部分，我们介绍了利用扫描隧道显微镜(STM)对SmB6的表面研究。通过STM的研究，我们了解到SmB6的解理截面具有非常复杂的性质。它具有多种重构类型，而且有证据表明不同的解理表面区域可能会与不同的ARPES信号相关。通过这一部分的介绍，我们想传达一个信息，即想完全理解SmB6的能带结构，需要具有一定空间分辨性质的ARPES来对它进行系统性的研究。

第六部分，我们介绍了SmB6中一些其他的物理性质，主要包括了Sm的混合价态问题以及SmB6中的反常量子振荡。SmB6中的Sm离子混合价态效应是个老生常谈的问题，但是最近的一些研究反映Sm离子的价态在表面和体之间出现了分离，其结果产生了一些有趣的物理现象。此外，众多以寻找二维费米面为出发点的SmB6的量子振荡实验却发现SmB6具有一个三维的费米面。沿着这个证据，越来越多的工作开始研究这个三维费米面是由什么构成的。

在这篇综述中，笔者以尽可能准确的物理语言来描述SmB6相关的物理图像，然而由于水平所限，难免有错误。对于有志于相关方向研究的物理研究人员希望了解更多的背景和相关知识，我们推荐以下两篇英文综述，Piers Coleman等人所著[7]，James Allen所著[8]。前者以理论为主，而后者则囊括更多实验内容。

II.SmB6的基态理论描述

SmB6，是一个简立方CsCl型晶体结构，钐离子位于立方晶格的八个顶角，六个硼离子形成一个正八面体，B位于立方晶格的中心（如图1）[9]。它的奇特性质的发现得益于冷战时期物理学和材料科学的突飞猛进。1969年美国的Bell实验室的Menth等人发现了六硼化钐这个材料在直至0.35 K的低温下都不能形成长程磁序[10]，这相对于其他的六硼化物差异巨大。且SmB6在低温下的金属–半导体相变机制也一直是一个谜团。直到1992年，Gabriel Aeppli和重费米子领域的领军人Z.Fisk教授建立起了关于SmB6的相变的物理图像，指出Kondo关联是SmB6产生相变的原因，并给这一类的体系命名为“近藤绝缘体”。简单地讲，Sm在费米能级附近的4f轨道电子在低温下逐渐获得局域相干性，从而产生了较强的局域磁矩，而巡游的5d电子则很容易被局域磁矩捕获从而屏蔽了局域磁矩。在准粒子的能带角度，便是4f/5d电子的杂化而在费米能级处产生了一个很小的能隙，从而实现了低温下的金属–半导体转变。而且由此可见，Kondo效应的唯象本质是自由电子对局域磁矩的屏蔽效果，是阻碍磁有序发生的，这也解释了SmB6在极低温下仍不能形成磁序的原因。关于重费米子体系中Kondo屏蔽和磁相互作用（主要是RKKY作用）的竞争关系，以及由此产生的Doniach相图等内容，可以参见[11]，本文不再赘述。

近藤绝缘体是一种相对容易理解的重费米子材料，虽然这种材料是强相互作用的电子系统，但它们的激发态和基态可以视为与非相互作用带绝缘体绝热连接，时间反演不变带绝缘体可以根据其基态波函数的拓扑结构进行分类，在2010年Maxim Dzero和Piers Coleman等人证明近藤绝缘体也可以进行拓扑分类。由于这些材料的强自旋轨道耦合特性，他们首先预测一部分近藤绝缘体在拓扑上是非平庸的，具有奇异的表面激发行为。之后他们利用周期性安德森晶格模型，成功建立了一个拓扑近藤绝缘体模型，开发了3D拓扑绝缘体的理论[6]。

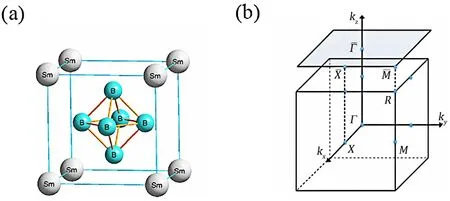
图1.SmB6晶体。(a)SmB6的CsCl型结构属于Pm3m空间群。Sm离子和六个B离子形成的八面体分别位于立方晶格的角和中心。(b)SmB6的体和表面布里渊区。(引自文献[9]图1)

Dzero与Coleman等人从周期性的安德森Kondo晶格哈密顿量开始，取

宇称在高对称点取决于δm=sgn(ξk∗m−εf)。四个独立的Z2拓扑指数[13]（一个强指数和三个弱指数）可以从δm构建：(i)强拓扑指数是所有的八个δm产生的：=±1；(ii)通过设kj=0（j=x，y和z），组成每个都包含高对称点的三个高对称面Pj={k:kj=0}。在这四点的宇称乘积定义了对应的弱拓扑指数，δm=±1。3D中三个弱拓扑指数的存在与2D系统的Z2拓扑指数有关（弱3D拓扑绝缘体类似于一沓2DZ2拓扑绝缘体）。因为有3种独立的方式来堆叠2D层形成3D系统，所以独立的弱拓扑指数的数量也是3。

传统的能带绝缘体具有全部的四个指数ISTI=而一个指数I=(−1)表示Z2拓扑态具有奇数个表面狄拉克锥态，对于一个的近藤绝缘体，ISTI=−1，因此，Kondo绝缘态是一种强拓扑绝缘体，它对于非磁性的无序扰动并不敏感。原则上可以针对不同的带结构和不同的εf值找到弱拓扑绝缘体和拓扑平庸绝缘体，如图2所示。除此之外他们还提出了计算特定晶格结构的Z2拓扑指数的实用方法，具体可以参阅文献[6]。

图2.重整f能级相对于导带底的位置不同，拓扑非平庸态不同。在布里渊区的高对称点处，强和弱拓扑指数以及δi显示为重整归一化f能级相对于导带底部的位置的函数。对于∈k=−2t∑a=x,y,z cos k a形式的简立方紧束缚谱，可以实现拓扑强、弱Kondo绝缘行为以及常规带绝缘体(|εf|>6t)。（文献[6]图1复现）

根据以上理论，他们预计f电子接近整数价的材料可能是弱拓扑近藤绝缘体，因此在无序方面是不稳定的。由此他们提出了第一个候选拓扑近藤绝缘体SmB6这个有趣的例子，其LSDA+U能带结构计算显示f能级的位置大约等于带宽的六分之一，与芯能级光谱测量的f能级n f∼0.7一致[14]，SmB6的准粒子f能级靠近分隔STI和WTI相的边界。

作为强关联拓扑绝缘体的第一候选材料，其最有趣的问题或许与关联电子在螺旋表面态中发挥怎样的作用有关，因此构建现实易处理的紧束缚模型成为理解SmB6物理性质的第一步。

同众多的弱关联性的拓扑非平庸体系对比，SmB6最外层轨道f电子具有明显的关联效应，给出其基态的理论描述更为困难。Yanase、Harima和Antonov等人详细的第一性原理计算给出了SmB6的能带结构和杂化性质描述[15,16]。他们的计算显示，Sm-4f轨道与Sm-5d轨道发生了杂化现象，5d轨道受晶体场作用分裂导致在Γ点产生一个eg双重态(doublet)。在远离Γ点的地方，eg轨道分裂成两个Kramers双峰，能量较低的一个在X点穿过了4f带。两条带的杂化使4f态从价带到导带，在X点形成重4f电子能带口袋。一旦d带在三个X点穿过f带，只要没有其他的穿越，由此产生的非相互作用的能带结构不可避免地是拓扑的，独立于f多重态的各细节（见图3）[7]。

图3.SmB6中f和d态在X点的带穿越示意图。(a)未穿越带。全满电子的4f 0带是一个常规的能带绝缘体。(b)穿越带。在X点的f带下方d带断开，取代一个奇宇称的f态，使之从价带到导带，由此产生的(-1)3标志着Z 2指数反转导致拓扑绝缘相的形成。(文献[7]图7复现)

2011年，T.Takimoto等人基于第一性原理计算结果特征的详细模型计算，预测 SmB6是一个强拓扑绝缘体 (strong topological insulator)[17]。他首先利用第一性原理计算结果构建了一个哈密顿量，继而利用这个哈密顿量计算出拓扑指数(topological indices)(v0;v1,v2,v3)[12]=(1;1,1,1)，证明了自己的预测。那么作为一种拓扑绝缘体，表面带色散在表面布里渊区的时间反转不变点处应该有狄拉克锥，且每个表面有奇数个狄拉克锥[12]。于是他们利用表面格林函数作出SmB6[001]表面能谱图，果然看到了三个狄拉克锥。无独有偶，2013年，香港科技大学的F.Lu等人基于相似的计算方法得出了同样的结果[9]，由于SmB6存在空间反演对称性，他们通过计算8个时间反演不变动量点处占据准粒子态的宇称性来确定其拓扑性质，如图4(a)中的表格所示，除了X点宇称性皆为+，因为整个表面布里渊区共有三个等效的X点，所以SmB6的Z2拓扑指数必须是奇数，结果为具有拓扑指数为(1;111)的强相关拓扑绝缘体。为了看到SmB6的拓扑表面态，他们利用Wannier函数构建一个紧束缚模型，它可以非常精确地再现LDA的能带计算结果。继而在40个原胞上结合紧束缚哈密顿量和旋转不变的Gutzwiller方法可以得到(001)面的表面态。所得的能带见图4(b)。可以很清楚地看到表面态包含三个狄拉克锥：一个位于表面布里渊区的，另外两个位于点。投影到(001)表面布里渊区和两个点的有趣的多狄拉克锥行为在现有的TI中非常独特，而且是在点能带反转的自然结果。

图4.计算所得SmB6的拓扑性质。(a)SmB6的拓扑指数。上半部分为布里渊区时间反演不变点Γ,X,R和M占据态宇称本征值的积。(b)SmB6(001)面的表面态。表面态基于投影Winnar函数结合LDA+Gutzwiller获得。(插入)(001)面表面态的费米面。(引自文献[9]表1，图5)

应当注意的是，上述第一性原理对SmB6的准粒子色散行为的阐述是一种基态性质。但是SmB6中的f轨道电子随着温度变化有着丰富的激发性质，并因此导致了其金属–绝缘相变行为(metal-insulator transition,MIT)[18,19]，在下文中，我们将结合它的电输运性质对其相变和关联行为给出一个合适的物理图像描述。

III.电输运性质研究

对于SmB6的研究已经有五十年左右[10,20,21]，作为第一种被发现的近藤绝缘体，它的低温电输运性质长期以来是一个未解之谜。随着温度的降低，SmB6的电阻率呈指数增长的趋势。众所周知的是，这是在Sm的f轨道在低温下逐渐局域化并形成局域磁矩的过程，通过短程磁相互作用，巡游电子局域通过屏蔽f轨道的局域磁矩而局域化。事实上这还牵涉到在重费米子中磁矩的短程和长程相互作用RKKY的竞争关系，并由此产生了著名的Doiach相图，该相图为理解重费米体系提供了一个基本视角。但是在本文中我们不对Doiach相图中的物理进行延伸，对于重费米子物理有兴趣的读者可以阅读下列文献[22–25]。

SmB6的R(T)曲线在很大的温度范围内(T>5K)都满足1/T和lnR的正比关系，可以用经典的半导体载流子热激发的Arrhenius关系来描述，即

并且通过斜率确认其激发能大小约为Ea∼10 meV。但是这个关系在5 K以下时却不再有效，其电阻率趋于饱和，似乎窄能隙半导体物理图像不再能描述极低温下的SmB6电运输行为，而极低温下SmB6不再具有能隙。低温到高温呈现非常规的电阻比率（见图5(a)）[26]，而且通常质量越好的样品呈现更高的比率。

图5.SmB6的独特电输运性质。(a)SmB6电阻率与温度的关系。箭头指向标明曲线所对应的坐标轴(引自文献[20]图1)。(b)SmB 6、BaB 6和CeAuSb2样品的电阻与厚度相关性。在低温下(T<4 K)，SmB6具有非常明显的厚度无关性，其三种不同厚度的电阻比收敛到1：1，表明随着温度降低到10 K以下，体（绝缘体）与表面（导体）分离。相比之下，BaB6和CeAuSb2显示出传统的体导电行为。(引自文献[29]图1)

至于为何在5 K电阻率出现了饱和行为，理论学家一直在给出不同的解释。但是多数的理论解释都认定5 K以下的SmB6的电阻饱和行为来自于体性质，并给出了多种机制，有些归结于能隙中可能存在的杂质态[10,27,28]。然而，实验学家通过构造巧妙的实验设计，揭示出在极低温下SmB6存在着一个特殊性质的导电通道。它具有极强的二维特性，且对于SmB6中的非磁性杂质完全不敏感。下面我们会主要介绍这些巧妙的实验设计以及实验结构。

第一个实验是加州大学欧文分校的Kim等人完成的[29]。根据三维体系的欧姆定律，长方体状的导体电阻率由测量电阻和几何因子A/L定义，L是长度，A是横截面积。因此，如果三维近藤绝缘体从高温下常规体导体转变为低温下仅具有表面传导的绝缘体，则样品厚度不应该影响测得的低温极限电阻，而应与其无关。图5(b)展示了SmB6这种不寻常的行为，体和表面产生电阻的厚度无关性，这正是理想近藤绝缘体的必要条件。通过对同一块样品的表面逐渐打磨至更薄[29]，从室温到10 K三种不同厚度的SmB6的电阻比与样品的厚度呈反比，这是典型的三维电输运特性。但是在10 K以下，电阻比开始下降并在5 K以下时不同厚度样品的电阻比值迅速收敛到1:1。这个低温下不同厚度样品具有相同电阻的性质表明表面电导占主导优势，且体微小带隙引起的有效温度效应留下了更小的电导，这表明在低温下体绝缘和金属态表面分离。

这些测量结果也与Kim与Wolgast等人之前的工作在结论上有高度的一致性，即在低温下SmB6出现了二维的导电通道[30,31]。与SmB6相比，半导体BaB6以及另一种近藤化合物CeAuSb2在整个温度范围仅显示出体金属行为，且其电阻对其样品厚度显示出了严格的反比关系。

除此之外Kim等人也利用不同几何形状以及不同生长批次的高质量SmB6晶体展示了其厚度相关的表面霍尔效应以及非局域传输特性[32]。这些结果揭示了SmB6的体绝缘和表面传导。

霍尔效应测试在楔形SmB6晶体上进行，如图6(a)所示，样品放在垂直磁场→B中，电流I在楔子的两端流动。霍尔电阻R xy=V x y⁄I是在不同的厚度d测得的。对于一般的三维导电体系，存在关系：R xy⁄B∝1⁄d，即总载流子和样品的厚度成正比关系，然而如果电导行为是二维性的，则总载流子R x y⁄B是与厚度无关的。在这两种情形下，其中一种可以定义与磁感应强度B无关的霍尔系数RH=E y/j x B，j x是电流强度（表面或体），E y是横向电场。在弱磁场中，霍尔电压与磁感应强度B在所有温度下都呈线性相关（图6(c)(d)），但在强磁场中，其在5 K左右会变成非线性相关，这显示出了一种多通道传导的温度范围。在高温(20 K)或者低温(2 K)下，无论是体传导还是表面传导，严格线性相关的霍尔效应都显示为单一通道传导。对于最简单的情况：即存在一个表面传导通道（顶部和底部结合）和一个体通道，霍尔系数分别是RHS、RHB，电阻率分别是ρS、ρB，在磁场B中霍尔电阻R xy为：

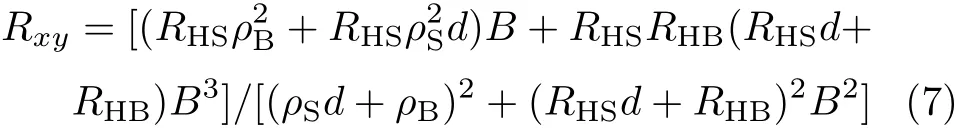
在强磁场下预计会呈现非线性关系，但是在弱磁场下其可简化为：

如果表面通道占主导（例如ρB≫ρSd），这确实证实了厚度无关性：R xy⁄B=RHS。笔者从B<1 T的诸多数据中提取出最具参考价值的、处于不同温度下的R x y/B[32]。图6(a)清晰呈现了楔形样品S1测试的代表性结果：样品不同位置厚度d不同（分别为120，270和320微米），而高温下厚度d不同R xy/B亦不同，但在4 K下它们都收敛到相同的数值0.3Ω/T，与表面传导相一致。这可能是因为如理论预测一般[9,33]存在超过一个表面通道，但在这个阶段很难定量分析表面载流子密度和迁移率。图6(b)重绘了霍尔电阻比率R x y(d1)/R x y(d2)，不难发现在高温下这些比率与电阻厚度之比d2/d1相等，在低温下皆为1。温度相关性可由一个双通道（表面通道和体通道）传导模型完美描绘，其体载流子密度随温度升高而呈指数降低，且有一个∆=38 K的激发能隙。利用这个简单的模型，在4 K的温度下可以在R xy/B曲线上再产生一个奇异的“峰”（图6(a)的实线），对这个“峰”迄今没有一个合理的解释[21]。低温下占据主导的表面传导可能也会产生与样品厚度无关的纵向电阻，近期也已被证实[29]。

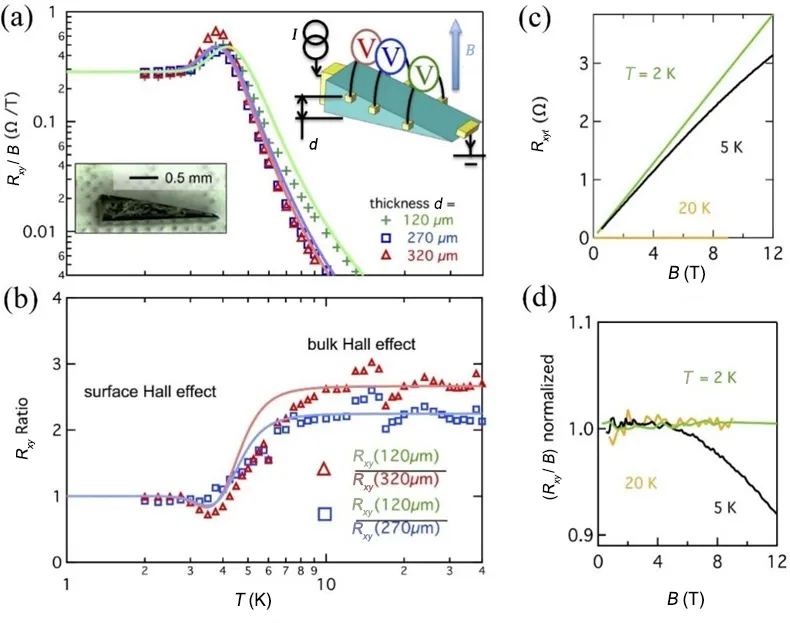
图6.SmB6的变温霍尔效应。(a)在楔形样品S1中，三种不同厚度下的载流子浓度随温度的变化关系。曲线是两个传导通道的拟合。左插图是晶体连线前的图片，右插图是测量示意图。(b)不同厚度下霍尔电阻R x y之间的比率，显示了随着温度的降低电子由体传导转变至表面传导。(c)在d为120微米时不同温度下的R x y/B，在5 K左右呈现非线性关系，证实5 K为由导体导电到表面导电的转变温度。(d)R x y/B归一化以证明其非线性关系。(引自文献[32]图1)

SmB6的这一系列的电输运结果具有非常重要的意义。传统的宽带隙的拓扑绝缘体，其体能带非常容易受到杂质的调控。例如在Bi2Se3系列样品中，由于缺陷的存在，Bi2Se3的费米能级往往落在导带上，因此所测得的电输运信号往往来自于体。即便是通过优化后具有较小杂质/缺陷浓度的Bi2TeSe2，其电输运中表面态所占的贡献也不会超过10%[34]。然而在低温下，SmB6作为一个近藤绝缘体，其费米能级严格落在体能隙中，而其电导信号几乎全部来自于表面电子态，如果可以证实SmB6具有拓扑狄拉克圆锥表面态，那么SmB6将会是一个理想的具有拓扑特性的电子材料。值得说明的是，尽管上述的电输运实验结果非常具有指向性，证实了其低温下由二维电输运占主导的结论，但是这些结果只能成为SmB6是拓扑近藤绝缘体的必要而非充分条件。换句话说，这只是在低温下观测到SmB6的导电表面态，而该表面态的直接证据应该由角分辨光电子谱或量子振荡实验来得到，这也是我们在下文中将要着重探讨的。

IV.ARPES谱学研究

ARPES是利用光电效应，通过受激发逃逸电子的能量和动量守恒的原理得到其在物体内部准粒子的能量动量关系（E−k关系）的实验手段，是研究材料内部电子结构的最直观方法。ARPES可以清楚地获得物质内部准粒子的能带色散行为，因此也被称为“能带显微镜”。ARPES的技术手段在80年代从传统的光电子谱中脱胎而出，在以铜氧化物超导为代表的强关联电子体系研究中取得了巨大的成功[35]。由于非平庸拓扑电子结构的一个非常重要的可观测量为表面/界面的具有狄拉克费米子色散关系的非平庸表面电子能带；而ARPES探测的低能逃逸电子主要来自于样品表面∼1 nm的深度，也就是说该技术手段对于表面态电子结构非常敏感，所以其对于确认拓扑绝缘体表面态具有非常关键的作用。因此自从拓扑绝缘体的概念被提出以来，ARPES成为了研究拓扑绝缘体的最重要的谱学手段。

简单地讲，在ARPES实验中，已知能量的光子照射在表面上，只要光子能量高于电子的逃逸势，电子便可以被激发离开材料，成为自由的光电子。通过能量分析器可以检测到光电子的角度和动能。电子的光激发是个复杂的量子力学过程，但是也可以进行如下简化，在光电子激发过程中，平行于表面的动量分量k x、k y守恒，但垂直分量k z由于界面的对称性破缺而产生了变化。通过引入经验性的内势V0可以拟合能带沿k z方向随着布里渊区的周期性变化，即

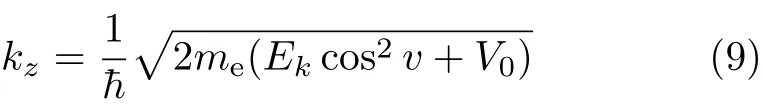
而电子的能量则完全可以由能量分析器直接给出。由此可以得出电子结构的基态准粒子谱函数A(E,k)的部分信息。之所以是部分信息，是由于ARPES探测出的准粒子色散依赖于实验条件所组成的矩阵元(Matrix elements)，其包括入射光自身的能量，偏振，入射夹角以及可能的电子末态等等。而获得准粒子基态谱函数的完整信息则需要不同条件的多次测试。

A.能带与能隙

正如上一节末所说的，SmB6电输运性质的结果指向了在该材料的表面存在着表面导电态，且非常有可能是拓扑非平庸性的，因此各研究组纷纷利用ARPES测定SmB6体态和表面态的电子结构。在2013年，国内外的多个研究组几乎在同时报道出观测到了SmB6的低能电子结构，而且发现了在体能系中存在的表面电子态，并论证了它的拓扑非平庸性，从而指证SmB6确实如理论预测是一个拓扑近藤绝缘体。下面我们会介绍这些ARPES的实验结果。

N.Xu等人通过调整入射光子能量，从SmB6的整个三维布里渊区获得了高分辨率的ARPES结果[36]，在该结果（图7(a)）中可以清楚地看到费米面由电子型能带组成的三个费米口袋，由于有费米面的存在，证实了该体系在低温下确实是一个导体，但是还需要验证费米面到底由三维还是二维的电子态组成的。

图7展示了在T=17 K下，随着不同的光子能量测得的SmB6的费米面和带色散，在不同的体布里渊区对应不同的kBz，图7(a)，是利用hv=26 eV的光子能量获得的费米能级处的等能面色散图，大概对应kBz=4π。图中是EF=±5 meV内的ARPES强度积分。从图7(a)可以看到，体布里渊区中不同的高对称点相同的费米面拓扑：一个小圆圈状的α能带，位于表面布里渊区的中心点，以及一个椭圆形的β带，位于表面布里渊区边缘点。还有一个作者认为由表面1×2重构形成的折叠带β′，其亦可在低能电子衍射图中看到。图7(b)则是图7(a)中三个费米口袋的E−k色散关系图。其中α能带非常弱，几乎无法辨认，仅能从MDC(Momentum distribution curve)上看到在点附近有些态密度。而β能带则是以点为中心，最为清晰。为了验证观测所得到的穿越费米能级的电子态是否属于表面态，作者对态密度最强的β能带进行了变光子能量实验（图7(c)），最后得到这条能带并不随变化的kBz而发生色散，因此可以证明其具有二维的特性。

几乎同一时间，复旦大学的J.Jiang等人也利用ARPES研究了SmB6的低能电子结构[37]。他们发现，在周围可以清楚地观察到四个大的椭圆形费米面（见图7(d)），其总面积覆盖了投影二维布里渊区的32.7%。在第二布里渊区中，周围的费米面轮廓很弱，而周围的光谱权重大大增强，这可能是光电发射过程中的矩阵元效应。这些态的二维性可以在他们的实验中同样利用k z色散进一步揭示。此外，美国普林斯顿大学的M.Neupane在同一时间对SmB6的ARPES实验结果[38]与上述结果非常类似，在这里我们便不再赘述。

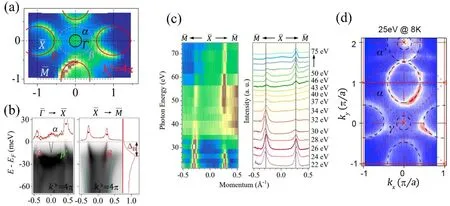
图7.ARPES所发现的SmB6(001)的表面态。(a)通过将hv=26 eV，E F=±5 meV内的SmB6(001)的ARPES积分，所得出的费米面。在点对应k z=4π。(b)对于k B z=4π平面，分别沿−和−高对称方向的ARPES能带图。红色和蓝色曲线是通过拟合MDC提取的β和γ带的色散。顶部的曲线是在E F处获取的MDC，其具有峰位置的标记。k空间中红色竖线标记处的EDC(Energy distribution curve)亦有显示。据此可以估计Kondo带隙∆∼20 meV。(c)沿−方向的ARPES强度与从25∼75 eV变光子能量实验结果，其沿k B z方向覆盖超过1.5个布里渊区，证实了这些能带的二维性。（引自文献[36]图1-3）。(d)用25 eV光子得到的SmB6费米面。其结果为(E F−5 meV，E F+5 meV)的窗口上积分结果。(引自文献[37]图3)

图8.SmB 6(001)不同区域呈现出的不同Γ点能隙态。(a-b)SmB6解理面两个典型区域(A,B)的价带光电子谱(a)沿着X−Γ−X方向，hv=70 eV的价带谱。(b)两种典型的表面区域的价态ARPES。(c)费米能级以下0.5 eV的光电子强度的实空间X Y扫描，以确定A和B两种表面所占据的位置。(d)来自A和B点以及第三种表面类型(C)的在沿着X−Γ−X方向的能带结构以及费米能级处的MDC，可以看到Γ点能隙态随着表面类型的不同而变化。(引自文献[39]图6)

然而上述的结果虽然证实了在体能隙中存在着二维的电子态，且其很可能就是拓扑表面电子态，但是SmB6的ARPES研究存在一个缺点，与传统拓扑绝缘体相比，它的Kondo能隙太小，只有∼20 meV。这对于利用ARPES观测到拓扑表面态的最直接证据 狄拉克锥色散结构提出了巨大的挑战。由于SmB6中的狄拉克锥结构一直没有被发现，因此人们对于上述ARPES实验结果往往有不同的解读。比如位于Γ点的较小的电子口袋表现出了一定的样品依赖，在有些表面区域并不存在这样的电子口袋。如图8所示，J.Denlinger等人便发现在解理截止面为Sm的样品表面（即图8(a),(b)中的A区域），围绕Γ点的表面态就会消失，只有在以B为截止面的样品才出现这些电子态（即图8(a),(b)中的B/C区域）[39]。众所周知拓扑表面态对于表面性质并不具有依赖性，它是体能带拓扑的表现。但是如果一但Γ点的电子口袋不存在，那么整个费米能级处的狄拉克锥便是偶数个。偶数个狄拉克锥意味着他们相互抵消后，它是拓扑平庸的。此外有实验组认为上述实验所发现的Γ电子态可能是来自于强自旋轨道耦合效应在表面形成的rashba劈裂态[40]，另外还有ARPES工作认为，这些表面态可能来自于表面悬挂键，并非本征的表面电子态[41]。因此认为SmB6是一个拓扑平庸的绝缘体。

图9.ARPES所发现的SmB6(111)的表面态及其可能的自旋构型。(a)SmB6的晶体结构。虚线三角形是(111)表面。(b)布里渊区示意图。蓝线是具有表面时间反演动量不变的二维表面布里渊区的第一个区域边界。(c)(111)表面的ARPES费米面，使用的是35 eV圆偏振光，在六个点（每个晶胞三个）显示出表面态费米面，因为所有点是等效的，因此表面的数量是奇数(引自文献[42]图1-2)。(d)具有B 6截止面的SmB6(111)面的费米面，显示了以点为中心具有Rashba型自旋螺旋的电子口袋。(引自文献[43]图4)

然而，日本大阪大学的Y.Ohtsubo等人在2019年设计的一个巧妙实验[42]回避了关于Γ点电子态性质的争论，他们通过单晶打磨的方法获得了SmB6(111)的表面（图9(a)），并利用ARPES获得了SmB6(111)的低能电子结构。研究在SmB6(111)的能带结构对于解析SmB6(111)的拓扑性质具有一个显著的优点，就是在SmB6(111)的二维布里渊区中，只有四个时间反演不变动量点，即一个点和三个点。在随后的ARPES实验中，作者确实观测到了以为中心的六个费米口袋。而在点周围则没有能带（图9(c))。再考虑到每个费米口袋代表了半个狄拉克圆锥，那么在SmB6(111)的二维布里渊区上，共观测到了3个狄拉克圆锥。在2021年，D.C.Ryu等人利用DFT对SmB6(111)截止面的能带结构进行了计算[43]，其计算出的(111)面由拓扑表面电子态所组成的费米面（图9(d)）同Y.Ohtsubo等人的实验高度吻合。因此该结果能够毫无争议地证实在SmB6的表面上存在着奇数个狄拉克圆锥，这是拓扑绝缘体的一个必要条件。

图10.沿着−−方向的拓扑狄拉克表面态的自旋极化构型。(a)SmB6的费米面。(b)费米能级附近沿高对称线−−方向的低能电子结构。取自(a)中的C1表示。红线是ESR（高于EF10meV）处的MDC。(c)表面态在x方向上投影的测量自旋分辨强度，红色和蓝色符号分别是自旋向上和自旋向下态的强度。(d)在ESR处测量的表面态沿x方向的自旋极化，红色和蓝色区域分别代表正和负自旋极化（自旋向上和自旋向下）。黑色和橙色箭头分别代表β和β′带沿x轴的自旋极化方向。(e、f)与(c、d)相同但是沿y方向。(g，h)与(c，d)相同但是沿z（面外）方向。图10中的所有结果都是用26eV的光子能量和右旋圆极化(C+)测量的。(引自文献[46]图2)

B.自旋分辨能带

在拓扑绝缘体中的自旋非简并表面狄拉克圆锥态具有一个非常重要的特性 动量–自旋的锁定关系(Momentum-spinlock)，即狄拉克圆锥在动量空间中的每一个点的自旋方向都与其动量k的方向呈现近似垂直的关系。这是在拓扑绝缘体中自旋非简并狄拉克圆锥的一个重要特性，也是判定其是否属于拓扑非平庸性的一个判定依据。而带自旋分辨的角分辨光电子能谱(Spin-resolvedARPES)是解析能带自旋方向的最直观工具。通过利用SR-ARPES[1,44,45]，人们解析了众多拓扑绝缘体的表面狄拉克圆锥的自旋构型，从而证实了它们的动量–自旋的锁定关系并确认其属于拓扑非平庸性。必须注意的是，下面我们介绍两个SR-ARPES，分别使用了Mott和VLEED的自旋探测器，这是迄今为止两种最常见的自旋探测器。经过长期的改进和发展，这两种自旋探测器的Shermanfunction，即自旋的分辨效率在10%∼20%之间。且SR-ARPES的能量分辨率较低，往往大于50meV。因此在解读其探测Kondo能隙中表面态的数据时，要理解其较弱的信号强度和较低的能量/动量分辨率。

图11.SR-ARPES发现的SmB6(111)的表面态的自旋构型。(a)在温度15K下，取自沿−的自旋极化MDC，使用线偏振的光子能量从15到39eV。取自费米能级以下60 meV。(b)由SmB6(111)上的拓扑表面态形成的费米能级处自旋构型示意图。箭头和带有叉和点的圆圈分别描绘了平面内和平面外的自旋极化。(引自文献[42]图4)

SmB6的狄拉克圆锥作为能带非平庸拓扑的可观测结构，其自旋构型同普通的拓扑绝缘体一样应该是自旋–动量锁定的，因此利用SR-ARPES的探测结果，通过上述的判定依据来判定SmB6的表面态是否是拓扑表面态。在2014年，N.Xu等人对SmB6(001)面进行了低能电子结构的SR-ARPES实验，其实验结果如图10[46]所示。在SmB6(001)解理面上，由于位于点的疑似狄拉克圆锥（即α能带）的SR-ARPES信号较弱，无法作为判定依据，其结论主要集中在以点为中心的能带（即β能带）上（图10(c)-(h)）。SRARPES的结果清晰地显示通过在接近费米能级处沿着ky方向切一条MDC进行自旋结构的分析，其自旋完全指向垂直于ky的kx方向（图10(c),(d)），ky方向以及外面的kz方向的自旋分量接近0（图10(e)-(f),(g)-(h)）。作者利用了不同偏振和不同能量的光子作为入射光来排除该结果可能来自于受激电子末态的干扰，其结果显示出了高度的一致性。该实验可以得出结论：以点为中心的表面电子s态具有非简并的自旋构型，且其自旋方向严格垂直于动量方向，呈逆时针的面内螺旋构型，且其自旋不具有面外分量。该结果非常符合之前在常规的拓扑绝缘体中狄拉克圆锥的自旋构型[47]。

此外，我们上文中所提及的 Y.Ohtsuba 对SmB6(111)也做了类似的实验[42]，即利用SR-ARPES研究在其体能隙中发现的表面态的自旋构型（图11）。在该工作中，作者探测到能隙中的表面态具有自旋非简并的特性，且其自旋方向与动量方向垂直（图11(b)），该结果同计算结果（图9(d)）也非常相似。但是有趣的是，该自旋构型呈现顺时针状，且具有自旋的面外分量（图11(a)）。

C.掺杂效应

在拓扑物态的研究中，掺杂是一个常用的调控手段。例如，通过对拓扑绝缘体的化学式中某一个或者多个元素进行替代掺杂，或者直接进行层间掺杂，可以对该拓扑物态进行全方面的调控。我们以最常见的拓扑绝缘体Bi2Se3为例，层间掺杂Cu可以让拓扑绝缘体Bi2Se3超导[48]；利用In对Bi进行替代掺杂可以削弱Bi2Se3的自旋轨道耦合，使其发生拓扑相变[49–51]；以及通过Sb替代Bi可以调控其费米能级，使其体态绝缘[51,52]。在拓扑绝缘体的研究中，利用磁性元素进行掺杂调控也很重要，其原因是Z2拓扑序属于受时间反演对称性保护的拓扑物态，而打破时间反演对称性必须引入长程磁序。另外一个重要的原因是，拓扑表面狄拉克锥都具有典型的自旋–轨道锁定关系，由于自旋守恒的关系，非磁性的杂质无法对拓扑表面态的准粒子产生背散射，只有磁性的杂质通过反转准粒子的自旋才能产生背散射行为。因而产生以下一个广为人知的结论，即非磁性的无序无法对拓扑狄拉克圆锥产生破坏性扰动[53–56]。同时，研究磁性和非磁性掺杂对拓扑绝缘体中的电输运影响和准粒子色散图像是一个非常重要的课题。

上述电输运工作中，Kim等人还利用SmB6的电输运性质，比较了磁性和非磁性掺杂对SmB6中电输运性质的影响[29]，他们利用Gd（钆），Y（钇）和Yb（镱）分别对SmB6进行了较低浓度的Sm位置的替代掺杂。图12(a)展示了在SmB6样品中的Sm位点上掺杂磁性Gd和非磁性Y和Yb之间的电阻温度变化（R−T曲线）的明显区别。Y和Yb掺杂SmB6两种不同厚度电阻比（电阻–薄/电阻–厚）在高温下同其样品厚度为反比关系，展示出常见的三维传导性质。但是不同厚度的样品在低温下(<10 K)收敛到1：1。相比之下，具有磁性Gd掺杂样品的电阻在整个温度范围内都与厚度呈反比关系。

此外，韩国光州科技学院的B.Y.Kang等人通过在SmB6中对Sm进行非磁性La（镧）和磁性Ce（铈）的替代掺杂，观测到了非常类似的结果（图12(b),(c)）[57]。La在化合物中通常为正二价，其最外层电子是4f0，因此为非磁性掺杂，通过对该体系不同厚度样品的R−T曲线进行比较，发现了La的掺杂并没有破坏低温下的二维输运平台。但是正三价的Ce的最外层电子为4f1，为磁性掺杂。在低温下，不同厚度的掺杂样品的R−T曲线在全温度范围内都表现出了随厚度呈反比的三维输运性质。因此可以认定在低温下，Ce的掺杂打破了二维输运平台。这与上述实验中磁性的Gd能破坏低温二维输运平台表现出了相同的特性。

图12.磁性与非磁性掺杂对低温二维电导平台的影响。(a)Y(3%),Gd(3%)和Yb(4%)掺杂SmB 6样品的厚度电阻比（低温下放大）（引自文献[29]图2）。(b)(c)La(3%)，Ce(3%)掺杂SmB6样品的厚度电阻比，插图为低温下不同厚度下的La(3%)，Ce(3%)掺杂SmB 6样品的电阻。与不破坏表面态的非磁性杂质相比，磁性杂质能破坏低温的电导平台，并改变其二维电导的性质。（引自[57]图2，图3）

上述实验的结果非常有趣，似乎指向了SmB6的低温二维电导平台更容易被磁性杂质破坏，而不会被非磁性的掺杂扰动。因此这也被认为是低温二维电导平台起源于拓扑表面电子态的一个重要证据。

D.磁性掺杂的ARPES谱学研究

然而上述的实验提出了一个事实，即我们有理由认定在SmB6的(001)表面观测到的体带隙中的表面态是受时间反演对称保护的拓扑狄拉克圆锥，而它对非磁性的扰动不敏感，但是它的输运特征可以被的1%的磁性掺杂破坏掉。对于熟悉拓扑绝缘体研究历史的人来讲，这是一个非常吊诡的结果。虽然引入磁序或者磁性杂质的方法是破坏时间反演对称性或者加强拓扑狄拉克准粒子背散射的一个重要机制，但是在往常的大能隙的拓扑绝缘体中，引入磁性杂质的方法只能通过微观的技术手段，如STM观测到背散射的增强。但是，通过宏观电输运测量或者谱学测量等手段，都无法观测到磁性杂质的引入对于拓扑狄拉克圆锥的整体性影响。因此，一个自然而然的想法便是，低浓度的磁性掺杂似乎扰动，甚至破坏掉了SmB6的拓扑表面态，而这种效应也许可以被ARPES观测到。

基于上述的猜测，作者所在的科研小组对分别掺杂了Eu（铕）和Ce这两种镧系磁性稀土元素的SmB6进行了ARPES的研究[58]，试图解析出其费米能级附近表面态受到磁性杂质的影响。Eu通常具有正二价的化合价，其最外层电子为4f7。而上文讲过，Ce的最外层电子为4f1，作者通过X射线吸收谱和光电子谱证实了二者的价态。所以Eu和Ce的自由离子都是具有磁性的。而且Eu和Ce都具有和SmB6同构的六硼化物，即EuB6和CeB6，因此Eu和Ce对Sm的掺杂非常可能是替代性的。而为了排除Eu或者Ce的掺杂导致相分离的可能性，作者对其新鲜解理的(001)表面进行了STM分析，得到了Eu或者Ce可以随机分布在SmB6中并替代了Sm。

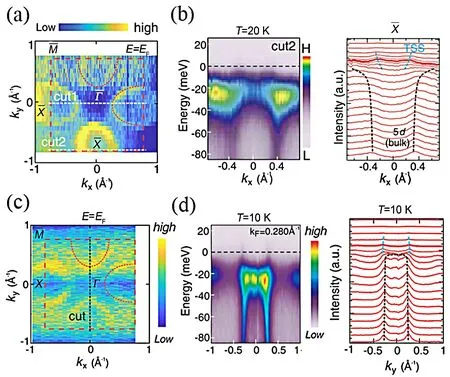
图 13.重磁性掺杂下的 SmB6(001) 的表面态。(a)Sm0.7 Ce0.3 B 6的费米面，虚线描绘了椭圆形表面态电子口袋。(b)沿着−−方向的ARPES切面。右图表面（蓝色）和体（黑色）能带标记在取自左图的动量分布曲线上，能量步长为5 meV。以上测试在T=20 K下进行。(c)Sm0.8Eu0.2 B6的费米面。(d)沿着−−高对称方向的低能ARPES切面。右图为费米能级50 meV内的原始数据曲线，能量步长为7 meV。以上测试在T=10 K下进行。（引自文献[58]图1-2）

在随后的ARPES研究中，作者发现了无论是Eu还是Ce，在高浓度的掺杂比例下（无论是20%的Eu的替代掺杂还是30%的Ce的替代掺杂），受掺杂的SmB6的费米面表现出了和SmB6高度的一致性（图13(a)(c)）。从ARPES解析的费米面来看，SmB6仍具有∼20 meV的体能隙，而在体能隙中能清晰地观测到表面电子态(图13(b)(d))。该结果显示，即便是在低温下，Ce等磁性原子的较低浓度掺杂可以破坏掉表面电子态的电输运平台，但是在谱学上，这些表面电子态在20%的掺杂浓度下仍保持了准粒子相干性，并没有受到破坏或者扰动的迹象。即便是在Eu的掺杂中，20%的Eu掺杂会在Sm1-xEuxB6样品中产生反铁磁序(TN=7 K)，形成一个新的磁性拓扑绝缘体，其表面电子态依旧保持完好。这样的结果似乎和电输运测量的结果出现了分歧，而且该结果也没有发现在拓扑绝缘体中过量的替代掺杂可能导致拓扑相变的现象。例如，14%的In替代Bi可以破坏掉Bi2Se3的非平庸拓扑序[50]，但是30%的Ce掺杂却无法破坏SmB6中的拓扑序。

为了解释SmB6的表面电子态在过量磁性掺杂下保持不变的奇异特性，作者对20%的Eu掺杂样品进行了变温ARPES的测量。在对于纯SmB6的变温ARPES测量中，发现了该体系的低能电子结构随着温度变化发生的相变行为，即随着温度降低，4f电子逐步形成相干性，在费米能级附近处形成了一条重费米子能带[59]。低温下，穿越费米能级的5d能带和4f能带发生了轨道杂化，从而在费米能级处打开了一个杂化能隙，而伴随着杂化能隙的产生，就出现了表面态电子。上述结果（见图14(a)）证实了4f电子轨道相干性与杂化能隙乃至拓扑表面态的依存关系。而对于Sm0.8Eu0.2B6样品的变温ARPES实验却得出了跟SmB6样品的变温ARPES非常一致的实验结果，随着温度的上升，未掺杂的SmB6和Sm0.8Eu0.2B6的4f能带有相干性随着热运动快速消失的过程，且与费米液体自能预期的温度趋势的平方(T2)一致。当T>120 K以后，用来标志4f轨道相干性的能级轨道半峰宽(FWHM)跃升至40 meV以上，表面态则伴随4f轨道电子相关性与杂化能隙的消失而消失（图14(a)）。该实验结果从另一个侧面论证了Kondo能隙和拓扑表面态的依存关系，即在SmB6中，只要保持4f轨道的相干性和直接Kondo带隙的产生，那么表面电子态就会存在。高浓度Ce和Eu的掺杂，从ARPES的实验结果看，仍然保持了4f轨道在低温下的相干性，从而保证了表面电子态的存在。而从另一个角度讲，Ce和Eu的磁性掺杂随机分布在样品内部，从微观上或者局域上增加了巡游电子的背散射，但是并未破坏表面电子态的长程相干。这就解释了为何光电子谱的表面态没有变化，但是在输运上表面传导电子被磁性破坏。

图14.相干性、杂化和表面态之间的关系。(a)4f带半峰特征宽度作为一种温度的函数，并与未掺杂的SmB6进行比较。阴影区域表示低于该阈值的表面态ARPES下可见。该阈值取自CeB 6在低温ARPES观测到的4f相干态[60,61]。(b)示意图显示了跨越费米能级(FL)杂化间隙的表面态。k z=0时体态绘制为实线，k z投影的连续体态以浅黄色阴影显示。(c)示意图显示了与X点相交的拓扑近藤绝缘体体能带结构温度分辨演变。中：随着温度的降低相干性增加，拓扑反转的直接杂化间隙在带交叉点打开。右：随着温度进一步降低，Kondo能带结构内是否存在间接间隙决定了电阻率的趋势。(引自文献[58]图4)

随着上述实验结果的发现，会自然而然地引出一个新问题，如果在SmB6中继续提高对Sm的磁性掺杂浓度，会发生什么情况。抑或是究竟掺杂浓度提高到多少，才能实现拓扑量子相变，使其体能隙中的表面态消失。带着这样一个疑问，利用更高掺杂浓度的样品，其中Ce的掺杂浓度高达50%，而Eu的掺杂浓度高达30%，Y.Xu等人对这些样品进行了进一步的研究[62]。其基本结论是，虽然在提高掺杂浓度的样品中，体能隙中的表面态的信号随着掺杂浓度的增强被进一步地压制，但是在所有的样品中都在低温下观测到了表面态，进一步证实了在SmB6中拓扑表面电子态对于磁性杂质依旧具有极强的鲁棒性。

在对于更高磁性掺杂浓度的Sm1-xMxB6(M=Eu,Ce)系列样品研究中（见图15），由于他们使用了氦灯紫外光源，对于费米能级附近的表面态电子的分辨能力欠佳，因此使用d轨道电子在费米能级处的弯折作为拓扑表面态的一个指标性信号。对于所有样品，高温(T=180 K)下的通过MDC的拟合得到的d轨道色散为线性（图15(b)为拟合总结）。而随着温度降低，在T≤80 K及以下，d轨道的色散关系在费米能级附近出现了符合存在表面态预期的偏折现象。从而论证在该系列所有的样品中都具有拓扑表面电子态。

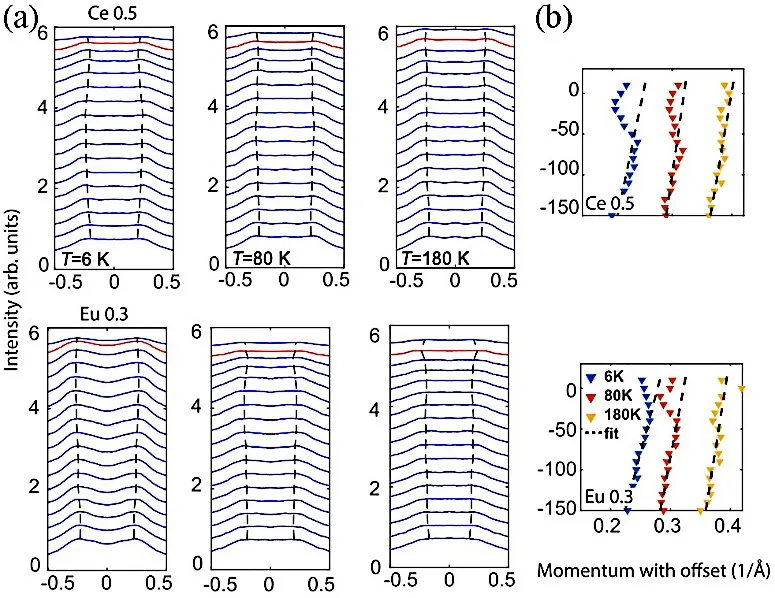
图15.30%的Eu和50%的Ce掺杂下SmB 6的表面态。(a)Eu0.3和Ce0.5掺杂的温度函数。在温度T=6、80和180 K下，对于每种掺杂，以10 meV的间距绘制了费米能级150 meV内的MDC。费米能级用红色曲线表示，黑色虚线标记拟合的峰值位置。(b)通过拟合得到的T=6、80和180 K时每种掺杂的色散关系。5d色散的线性拟合是在−150到−50 meV能量窗口获得的，并显示为黑色虚线。(引自文献[62]图3)

作者试图通过多个方向解释该实验结果。他们认为如文献[58]中所猜想的那样，50%的Ce或者30%的Eu掺杂依旧没有破坏掉f轨道的能带相干性，从而该体系的拓扑表面电子态得以保留。另一个猜测的方向则是认为磁性的替代掺杂对于该体系的作用非常局域，其影响范围只有几个晶格常数。而另一方面未受到掺杂影响的小范围独立区域依旧以纯的SmB6形态存在而拓扑表面电子得以保留，这一猜想也得到了一些理论工作的支持[63]。无论上述哪种解释更为接近其背后的物理真相，50%的替代掺杂都无法破坏掉拓扑表面电子态这一实验结果，都值得更多的实验以及理论来解释它背后的物理。

V.SmB6的表面重构研究

上述的ARPES研究工作对于SmB6的拓扑性质给出了一些关键性证据，然而在SmB6的研究中，有一个无法忽视的问题，即ARPES是一个表面物理探测手段，其所探测到的逃逸电子完全来自于表面1 nm以内的深度。但是无论是SmB6的(001)或者(111)解理面，都是极性表面，非饱和的化学键让SmB6的解理面具有活跃的表面性质。虽然一个单晶的体能带的拓扑性质与解理面的性质无关，但是在一些ARPES结果中，SmB6的一些关键性的电子结构表现出了与样品表面不同区域的依赖性，比如J.Denlinger等人便发现了普遍被认为是拓扑表面态的以Γ为中心的口袋会随着ARPES光斑照射样品位置改变而改变，这便对其是否具有拓扑性起源提出了疑问[39]。此外，H.He等人还发现了SmB6的Sm离子的价态会随着时间和温度产生不可逆的向高价态演变的情况，和体的Sm离子发生了价态的分离[64]。马里兰大学的Y.Nakajima等人和香港科技大学的C.Yue等人分别认为在SmB6的表面上可能产生表面的磁有序，以及更低阶的一维/二维拓扑序[65,66]。因此研究SmB6的微观表面结构和性质则具有非常重要的意义，它不但作为补充证据，完善ARPES对于SmB6的研究，更能够验证在SmB6中可能出现新的奇异量子现象。

SmB6(100)是它的自然解理面，一般的SmB6(001)解理面都会包含两个截止面，即Sm离子截止面和B6离子截止面。这两种截止面的表面性状差异非常大，而一般的解理都会在同时包含这两种截止面。相对来说，B6截止面的形貌会简单得多，由于六个硼原子由共价键构成一个紧闭的正八面体笼状结构，所以它的表面性质相对稳定。但是Sm离子的截止面则复杂得多，它会形成多种重构现象。下面我们会结合多个文献报道的情况进行介绍。

使用STM对解理面(100)表面的研究发现了各种表面形态和/或重构[67–69]。在图16(a)-(d)中，呈现了(100)表面在60×60 nm2区域上的STM图像，这种Sm截止面的表面重构的区域可以达到几微米的尺度，其尺度小于常见的ARPES的光斑尺度。任何一次的解理可以产生所有这些不同类型的重构，表明这些不同的Sm的重构的能量比较接近。图16(a)、(b)和(d)中的重构相对复杂，是多种重构的混合，不能形成一种长程的有序态，而(c)显示的是简单有序(2×1)重构，这种重构非常常见，在STM和LEED中经常被观察到[70,71]。

S.Rößler等人还做过SmB6无重构表面更小范围的STM研究[68]，如图17(a)，(b)。沿着图17(a)、(b)中的白线高度扫描，其表面形貌在图17(c)、(e)中，沿〈100〉方向进行扫描，其形貌的周期间距等于SmB6的晶格常数a0=4.12Å。除了相应的晶格形貌，在图17(b)中还有沿着〈110〉方向上的周期性结构：沿〈100〉方向扫描其形貌，即图17(b)和(e)中标记为2的蓝线，其显示出间隔大约为因此，图17(a)的表面归因于B的截止面[67]，而图17(b)代表Sm的截止面[73]。后者表面出现深度约80 pm的凹痕（见图17(e)中的蓝线2），对应于Sm截止面上Sm与最顶部B原子之间的高度差。这表明这些凹痕是由Sm的空位引起的，可能是在解理样品时从Sm表面层剥离出来的。相比之下，在图17(a)的B截止面上，没有发现表面缺陷。

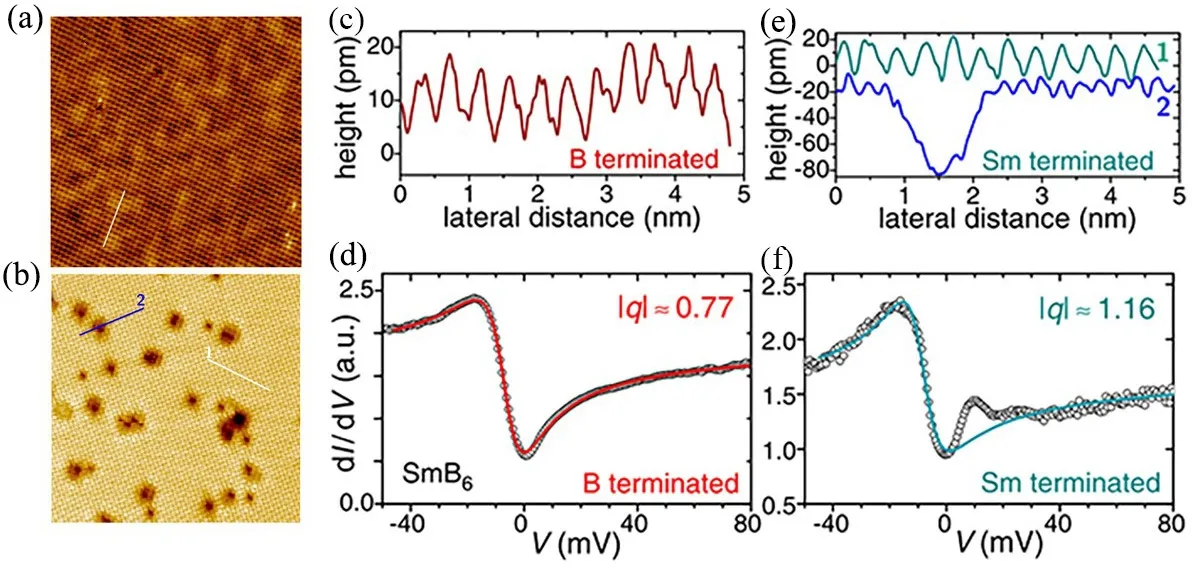
图17.非重构B截止面和Sm重构截止面之间的比较。(a，b)B截止面(20×20 nm2)和Sm(17.4×17.4 nm2)截止面的形貌。(c、e)沿(a、b)中标记的线进行扫描。白线平行于〈100〉方向；(b)和(e)中的蓝线2沿着〈110〉方向。(d、f)4.6 K下分别在B截止和Sm截止面上的STS（圆圈）以及利用法诺共振进行的数据拟合，取得的q值在图中标明。(引自文献[68]图4)

在这样一个扩展的非重构B表面上进行扫描隧道光谱学(STS)测试提供了dI(V)/dV曲线，如图17(d)所示，当T=4.6 K时。STS谱显示出了明显的法诺线形，即STS出现了法诺共振(Fano resonance)，它是由于针尖隧穿到两个耦合通道[74]，即导带和4f准粒子态[75–77]产生的。这两个通道相对于EF的能量位置或电子结构也有可能发生相应的变化[78]。由此产生的隧穿电导可以表示为[79]：

这里，Γ表示的是谐振宽度。不对称参数q与隧道进入4f态与进入导带的概率之比以及导带的粒子–空穴不对称性有关[76]。方程10成功应用于单杂质Kondo效应[80,81]以及Kondo晶格系统[82,83]。相应的拟合（图17(d)中的红线）产生Γ=16.5 mV，该值与上述杂化间隙的宽度非常吻合。正如对于B截止面所预期的那样，|q|=0.77小于1，这与进入导带的主要隧穿一致。注意，此处显示的不对称性与重构表面[67]上的其他STM测量结果一致，但与点接触谱的结果相反[73]。

对于在Sm截止面上获得的STS，观察的总体结果非常相似（图17(f)），除了在10和25 meV左右的两个额外激发。如果忽略这两个激发，该数据亦可以进行良好的拟合（图17(f)中的线）。由此获得的值Γ=16.4 mV与B截止面的值相同。然而|q|=1.16表明一个更明显的隧穿进入4f准粒子态，这与Sm作为截止面相关。在同样基于隧穿机制的早期点接触谱测量中也观察到了这两种额外的激发[84]。可以推测，在较小的非重构Sm表面上，25 meV处的激发在−27 meV处具有其对应物，具有相反电压符号的相应特征被其他更显著的激发所掩盖。

W.Ruan等人曾利用扫描隧道显微镜对SmB6的表面重构现象进行了系统的研究[69]，与前面的研究不同的是，他们的SmB6样品是在室温下解理的，室温下的表面弛豫动力学过程会让其表面形貌和低温解理完全不同。在高温解理下，最显著的结果是B6的笼状结构可以被打破，Sm和B离子会协同产生一些新奇的表面重构现象。例如（图18(a)）具有一个原子级平坦方形晶格，但是两个相邻原子之间的距离∼3Å，或者为a0图18(e)展示了Sm-B网络结构示意图。其形貌图展示了一个弱结构。图18(b)所示的第二相也呈现出方形晶格，其周期性与SmB6的晶格常数一致，应该是未重构的B6截止面。图18(c)中表面形貌由不完整方形晶格的“甜甜圈”状组成，然而“甜甜圈”的原子是未知的，但它们很可能是图17(a)中Sm重构截止面的正方形中心的四个B原子，因为这些“甜甜圈”的高度约为1Å。图18(d)中显示的第四相也表现出甜甜圈状(“D2”相)图案，但这里的“甜甜圈”具有更大的直径。此外，下层方形晶格的晶格常数等于a0=4.1Å。这个相的结构是很明确的。如图18(h)所示，“甜甜圈”由八个硼原子组成，这些硼原子通过硼八面体内的解理暴露出来，它们位于A2相的方形晶格上。在这四种表面结构中，D2相是主要相。可以注意到的是这里的表面形态与其他两组报告的形态不同[67,68]。

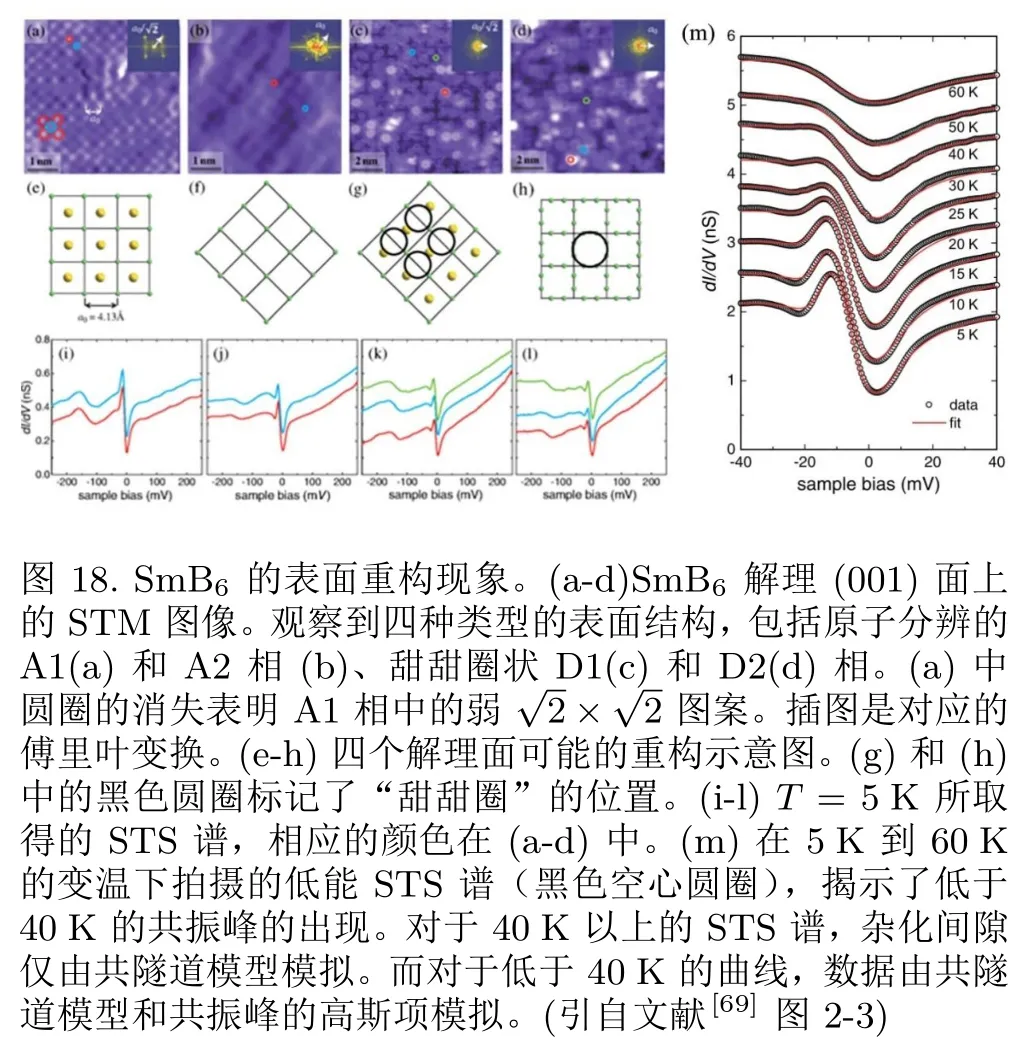
图18(i-l)展示了偏压(V)与dI/dV的变化关系，态密度在T=5 K取自四种类型的SmB6(001)表面。尽管表面形态明显不同，但整体dI/dV线形状彼此高度相似。能隙和大的零偏置电导也与在解理SmB6上的点接触光谱中观察到的相似[73]。这就表明该体系的电子结构受表面层原子及其重构的影响很小，间接意味着可能存在某种表面电子态。随后他们进行变温电子谱测量，在图18(m)中，他们放大了具有dI/dV曲线（黑色空心圆圈）的更详细T变化的低能量范围。不难发现杂化能隙随温度升高逐渐减小，但一直到60 K仍未消失。然而能隙内的共振峰迅速减小，在40 K即消失，在最低T=5 K时，光谱表现出强烈的不对称线形，尖锐的峰谷共振位于能隙的下边缘，而该温度尺度与输运和磁化率测量发生明显转变的特征温度吻合。理论研究表明该共振可能来源于Kondo晶格中自旋单态到三重态的多体激发模式，对材料的输运和磁性质有着重要的影响。

我们之所以在该部分着重的讨论了SmB6的解理表面形貌，而并未展开讨论它的表面STS研究，是因为这部分结果与上面ARPES研究息息相关。我们希望在不久的将来，越来越多的具有纳米级光斑的Nano-ARPES对上述各种不同的截止面和重构进行更为系统的电子结构研究，从而获得SmB6的更为全面的物理图像。

VI.SmB6的其他奇异性质

在以上的介绍中，我们看到了SmB6自从被人们发现可能是拓扑近藤绝缘体以来，所做的大量研究工作，主要以实验寻找它的拓扑表面态以及论证其拓扑非平庸性为主。然而，近年来对SmB6的研究报道远不止于拓扑物相方面，一些其他方面的新奇物性和有趣行为也已被发现，在这部分中，我们会主要介绍在SmB6中发现的表面–体价态分离行为，以及SmB6中反常的体量子振荡行为。我们认为SmB6中的这两个特性是非常有趣的，也是值得进一步深入研究的。

A.混合价效应

f轨道电子的局域-巡游双重特性，导致重费米子化合物常常无法用一个整数价态来描述，因而中间价态(intermediate valence)效应是较为常见的[85,86]。这也是为什么传统的DFT计算在描述重费米子体系的电子结构时，其结果和实验往往差异较大，需要引入动态平均场理论(DFT+DMFT)。SmB6中的Sm离子一样具有中间价态的特性[20,87–89]。在六硼化物中，EuB6中的Eu近乎正二价，在CeB6中Ce近乎正三价，而SmB6中，Sm离子属于中间价态，非常像正二价与正三价的混合，多种实验手段对其价态的测量大约处于2.5∼2.7之间，即可以近似的认为f轨道的占据态4f6与4f5的占比大概在50%:50%或者30%:70%[90]。

重费米子体系中的混合价态常常随温度发生变化。其原因是显而易见的，在上述掺杂效应的介绍中，可以看到温度对于f电子的相干性，乃至f轨道与d轨道电子的杂化等效应是一个非常重要的调控条件。而上述行为都会影响到f电子的局域–迅游特性。在重费米子体系中，价态随温度的变化可以引起一系列的特殊效应，比如电阻率对压力和磁场敏感的温度相关性[91,92]，甚至可能引起量子相变，也被称为价态量子相变行为(Quantum Criticality of Valence Fluctuations)。

X射线吸收谱由于较高的能量分辨率，完备的理论描述成为辨析化合价态的最重要和最准确手段。图19(a)显示了利用硬X射线吸收谱探测的SmB6中Sm离子平均价态的温度相关性，这幅图显示了三个特征温度[93]。在300 K下，Sm离子的平均价位为2.59±0.01，并且在300 K和120 K(=T1)之间恒定。然后它在冷却到50 K(=T2)时逐渐减小，并在50 K和15 K(=T3)之间稳定在2.50±0.01。在较低温度下，Sm价数在2 K时增加到2.52±0.01。这些结果通常与之前的测量结果一致。T1处的异常与之前的中子衍射结果一致，因为Sm2+离子半径大于Sm3+离子半径[94]。T2和T3异常与负热膨胀的温度范围[95]以及纵向弹性常数C11的温度相关性[96]一致。

图19.SmB6中Sm离子的混合价态。(a)SmB6中Sm离子平均价态的温度相关性。插图放大了低温区域。(引自文献[93]图2)。(b)J=5/2的表面老化趋势是根据J=5/2和J=0两种XAS曲线估算的。4.5小时后将样品加热到300 K，导致更快速的老化。暴露在空气中样品的J=5/2的占比用星号表示。(c)利用多重态模拟计算所得的J=5/2和J=0 XAS曲线。阴影区域表示基于（较暗）±0.1和（较亮）±0.4在t=3 h和5.5 h时单价位点密度的估计比率差异的变化性。老化趋势曲线中产生的误差由图(b)中相同的阴影表示。（引自文献[64]图4）

图19(a)的三个特征温度与SmB6中的特征能量合理吻合，T1对应于从电阻率（或光电发射光谱）估计的能隙∆=100 K（或130 K）[97,98]。这种对应关系意味着Sm价态与体能隙∆的形成有关。磁化率在T=T2处出现一个峰值，对应于另一个间隙。该温度也与根据电阻率测量值估算的活化能Ed一致[97]。此外，根据共振非弹性散射(NRIS)估计的声子能量的温度相关性在120 K(=T1)处显示最小值，在50 K(=T2)处显示最大值。T1和T2之间的负斜率显然与Sm离子半径有关。由于平均价反映了Sm的离子半径，其结果表明Sm声子能量与Sm位点的客体自由空间相关。在T=T3处，热膨胀系数显示一个小的峰值，这可能与Sm价态的变化有关[15]。在T=T3以下，Sm离子平均价数的增加与正热膨胀一致。总而言之，他们发现晶格常数和热膨胀的异常温度相关性确实与Sm离子的平均价相关。

然而在SmB6中，一个有趣的发现是，Sm的价态在体和表面中并不总是一样的。H.He等人研究了在真空中解理的SmB6的紫外X射线吸收谱，其能量范围覆盖N4,5共振吸收峰[64]。同上述硬X射线的XAS相比，紫外XAS所探测到的二次电子主要来自于表面的1 nm∼2 nm，可以说是一个表面敏感的探测技术。他们通过利用电子多重态模拟的方法解析了SmB6的紫外XAS随着时间和温度的变化（见图19(b)(c)），发现解理面的Sm的价态随着暴露时间的加长，由混合价态逐渐趋于正三价。在低温(T<20 K)刚解理的样品表面，4f5的占据比大概为40%，而在解理8小时以后，其表面Sm的4f5的占据比例可以达到70%以上。温度的提升会加速这种进程，但是温度的变化对于Sm趋向于4f5的进行并非必要条件。此外，与体的Sm的价态随温度变化的可逆性不同，表面的Sm的价态变化是不可逆的。通过利用多重态理论对于紫外吸收谱的拟合，表面Sm的4f6多重态基态总角动量为J=0。而Sm 4f5的多重态基态的总角动量J=5/2。4f6被认为是自旋单重态，几乎不可能被磁化或形成磁序。因此解理面Sm趋于4f5则可能使其表面更容易产生磁性。这种推测可以在高压实验中得到一定的证实。高压会将SmB6中Sm的价态几乎完全地推向正三价即Sm 4f5态，而同时SmB6会进入到一个磁有序的基态[39,59,99]，另外，Y.Nakajima等人在低温下发现了SmB6具有表面的铁磁序，并观测到了与量子反常霍尔效应类似的整数量子电导行为[66]。更为有趣的是，SmB6中的表面和体的价态分离行为以及表面更加趋向于4f5的行为会压制表面的近藤效应，近藤单重态的基态上释放出一些轻质量准粒子，从而改变了表面态的色散关系，增加了费米速度。由此也可以解释为何在ARPES中看到的费米速度通常比较高[100,101]。

虽然我们在本节中阐述了SmB6中Sm的中间价态和表面–体的价态分离行为，但是它们的物理图像，尤其是后者的物理图像还是不为人所了解。像我们在STM对SmB6的研究中所讲的那样，SmB6的解理面具有复杂的重构形貌，要想完全理解为什么在SmB6的表面具有价态的分离行为，需要结合表面物理的技术手段以及计算进行系统而针对性的研究。

B.Sm B 6的反常量子振荡

量子振荡是获得金属态费米面信息的最重要实验手段之一，通过量子振荡可以获取包括费米面大小、电子有效质量和弛豫时间等重要物理信息。连续分布的电子会在强磁场下劈裂成不同的能级，这一过程即为朗道量子化，而逐渐增大的磁场会使朗道能级之间的能量间隙逐渐变大，从而逐一地“通过”费米能级。这一过程的结果就是费米面上的电子态密度开始随磁场的变化而振荡，也就是这个材料的包括电阻率，磁化率等性质随着外磁场的变化而振荡，这一过程被简称为量子振荡。量子振荡是巡游电子在弱关联前提下的一个典型行为，因此是电子的费米液体行为的典型特征。

图20.SmB6晶体中的量子振荡。(a)两种方法生长的SmB6单晶的磁转矩数据解析出的FFT峰值。上下两幅图中的Cambridge sample FFT峰值分别与同一频率范围内的Michigan sample的d HvA振荡特征一起绘制。在这两组数据中，磁场从晶体[100]轴向[011]轴转动。虚线是2D圆柱体费米面模型的拟合[102]。(引自文献[105]图6)(d)图案比较了2D圆柱费米面模型和3D细长椭圆体费米面模型。(文献[26]图6d复现)

如前文所述，量子振荡依赖于占据的费米能级，即只有在金属中能发现。2014年，密歇根大学的G.Li等人第一次在使用助熔剂法生长的SmB6中观测到了de Haas–van Alphen振荡行为，即磁化强度的量子振荡行为[102]，并解释SmB6的量子振荡来自于SmB6的表面态，其三组费米面都是二维的，且电子有效质量只有0.1me。这一结果本来应该是对于包括ARPES和STM以及输运工作的非常好的补充，但是剑桥大学的B.S.Tan等人（Sebastian组）在观测到利用浮区法制备的SmB6中的量子振荡实验中却认为，SmB6中的量子振荡信号具有三维性质，而非起源于表面态[103]。有趣的是，这两个实验组在SmB6中观察到的振荡频率的角度相关性的结果表现出了高度的一致性（图20(a)）这表明这些dHvA频率是SmB6的内禀性质而且这两个工作是在研究来自相同电子态的量子振荡。但是参考文献[103,104]中使用的3D费米面模型是极其细长的椭球，与参考文献[102,105]早期研究中使用的2D圆柱费米面模型形成对比，显示了这些模型在大范围磁场方向上的重叠（图20(b)）[26]。

图21.不同程度抛光、蚀刻的SmB6晶体信号。(a)在几个不同的抛光步骤中样品的振荡转矩与反向场的关系。转矩与样品的质量成比例(m0/m)，并且从[010]几度处施加场。在去除最后的Al沉积物后，振荡消失。插图显示了样品的逐步抛光，描绘了分布在整个样品中的一系列Al沉积物。初始(100)表面不受干扰。(b)图显示不同程度抛光的SmB6晶体振荡转矩的频谱。波谱按样品质量(m0/m)进行缩放。插图显示了多晶Al熔剂的频谱。(引自文献[106]图2)

然而，有研究组对这些有趣而令人兴奋的实验结果提出了不同的看法。加州大学欧文分校的S.M.Thomas等人复现了文献[102]中的实验，利用转矩磁力计来测量助熔剂法生长SmB6在不同磁化强度中的量子振荡[106]。他们发现，助熔剂法生长的SmB6中往往会夹杂一些立方晶系的Al单晶，它的晶格常数非常接近SmB6且晶向一致。为了确定SmB6中量子振荡的可能来源，他们对许多助熔剂法生长的单晶包括抛光样品进行了量子振荡的测量。然而，只有一部分SmB6样品显示出磁化振荡行为。这些样品往往具有更大的厚度，但没有观察到与表面条件（即生长与抛光）的相关性。尽管具有相似的表面晶面和表面积，但一些样品中没有振荡，这是似乎表明量子振荡并非来源于本征的SmB6晶体。而后他们对表现出d HvA振荡的晶体进行不同程度的抛光、蚀刻（图21(a)插图）以确定量子振荡的起源，图21(a)比较了生长的与抛光一半的样品信号，图21(b)发现FFT(Fast Fourier Transform)振幅与样品的质量而不是样品面积大致成比例 与分布在晶体中的Al夹杂物引起的振荡一致。此外，尽管存在诸多Al夹杂物，但在频谱中观察到了显示出明显角度相关性的明确峰。继而他们将样品抛光成薄板，即使样品顶部的(100)表面没有受到干扰，在最终抛光和蚀刻步骤之后也没有观察到振荡，从而论证之前观察到的量子振荡效应的来源于SmB6中嵌入的Al沉积物。

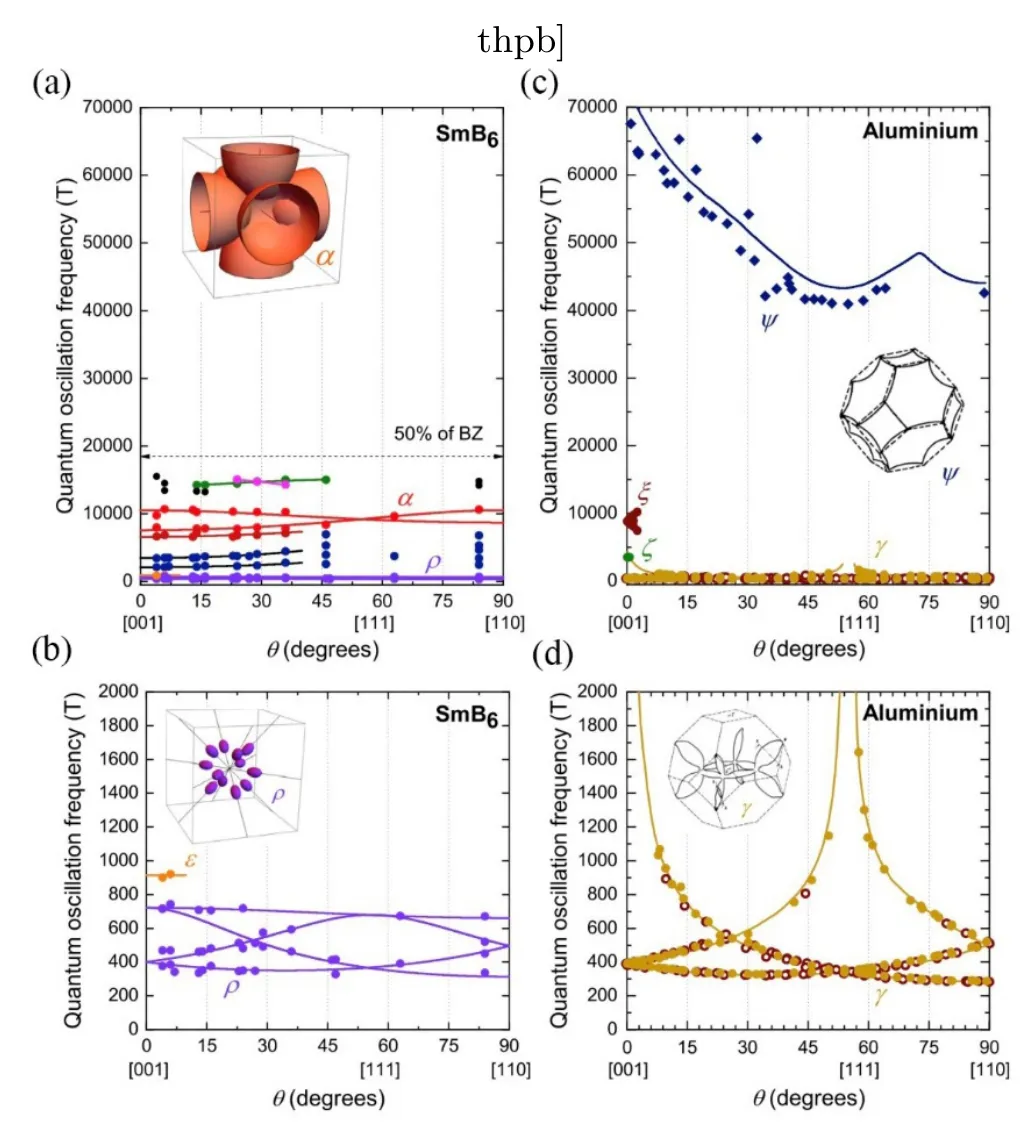
图22.SmB6与Al同频率量子振荡比较。(a-d)浮区法生长的SmB6（a和b）与Al（c和d）的[001]-[111]-[110]旋转面中量子振荡频率的测量角度相关性在相同频率尺度上的比较。(a)和(c)中高频分支的比较显示SmB 6的整个角度范围内有2 kT和16 kT之间的多个分支，但铝没有，铝具有超过40 k T的突出高频分支（圆圈是文献[107]测量的，方块来自文献[108]）。箭头表示假设单个球形费米面截面半填充的最大预计频率，在此之上我们不希望看到金属等效物的频率，类似于LaB6。(b)为SmB6发现的ρ分支具有平坦的角度相关性，对应于沿<110>的十二个椭球的费米面，如图所示。(d)此研究中测量的铝的频率与之前的测量结果（棕色圆圈[109]）。(引自文献[107]图9)

但是，上述工作却无法解释为何在浮区法制备的SmB6中所发现的与助熔剂法制备的SmB6中类似的量子振荡行为。在浮区法生长的SmB6单晶中观察到的高于2 kT的高和中量子振荡频率与在Al单晶中观察到的高频率振荡有着明显不同（图22）[107]。而低频量子振荡（SmB6中的ρ频率和Al中的γ频率）在300 T和500 T之间的范围内具有一些相似的特征，考虑到完整的角度相关性，则差异非常明显。Al的细长链状费米面使振荡频率沿[001]和[111]产生色散，不像在浮区法生长的SmB6单晶中的三维椭球费米面，在所有角度产生很弱的量子振荡频率色散。相比之下，G.Li等人在Al助熔剂生长的SmB6单晶中报道了沿几个对称方向的发散频率[102]。SmB6浮区法生长样品和Al的量子振荡之间的主要区别是SmB6中中频分支(2∼15 kT)的出现，其对应于主要的费米面部分，在Al中没有类似的部分。SmB6中的中频与元素Al中的非简并40-80 kT分支也形成对比，其在SmB6中并无相似之处。大振幅振荡、中频分支(2∼15 kT)和ρ频率的四个平坦分支的明示是SmB6中与三维费米面相对应的本征体量子振荡的清晰特征。由此推出在SmB6中的量子振荡是本征的体性质。

至于SmB6中量子振荡的起源，似乎有众多简单的自然而然的猜测，比如在该体系内，Kondo关联效应使费米液体不能准确描述SmB6。抑或是在强磁场下，SmB6形成了费米面，这些猜测都需要进一步的验证。另一个拓扑近藤绝缘体YbB12的研究似乎能得给出一些更可靠的证据。在2018年，YbB12中也发现了起源于体效应的量子振荡行为[110]。对于YbB12的进一步实验研究发现了在接近零温时它具有随温度线性增加的热导率和热容，预示着YbB12中存在着某种连续的费米子激发行为，但是它同时是电中性的和高度巡游的。这种电中性的费米子构成的费米面是YbB12，或者SmB6中的量子振荡的来源[111]。

事实上，在拓扑近藤绝缘体SmB6以及YbB12发现三维的量子振荡并不是在非费米液体体系中出现量子振荡的特例。在欠掺杂的超导母体YBa2Cu3O6+x中就发现了量子振荡行为，然而该体系很可能属于非费米液体相[112]。而最近在绝缘相的二维WTe2中也发现了量子振荡的行为[113]。因此，在SmB6中出现的具有体性质的量子振荡，很可能并非是该近藤化合物的特殊行为，对于理解其特殊的量子振荡现象，很可能需要从更高的视角来解决这个问题。

VII.展望

拓扑近藤绝缘体代表了三个研究领域 拓扑非平庸物相，强关联电子体系，表面科学的碰撞。因而需要三种不同研究背景的物理学研究人员的共同努力来揭示其背后的物理。也正是在这种背景下，其研究的发展和进展促进了三个方向的互相认识与融合。

通过本篇综述的展示与讨论，我们可以看到SmB6这个材料已经被广泛的接受为一种拓扑近藤绝缘体。它有清晰的表面电子态，这些表面电子态受到时间反演对称性保护并且在低温下主导了电输运过程。然而我们同样看到，在SmB6各种的实验测量中仍有一些互洽性问题，包括ARPES实验中磁性掺杂样品的表面电子态得到保存而电输运测量下低温的二维输运平台却被破坏的情况[29,57,58,62]。更让人无法理解的是，低温下的来自于体材料的量子振荡以及热输运信号似乎指明了在SmB6的体能隙中，还存在另一套来自于体材料的连续激发行为主导了上述实验结果[102,103,107,114–117]。至于这种激发行为是否属于费米子以及是否可以用经典的费米液体描述，我们都不得而知。此外，近些年拓扑量子材料的研究突飞猛进，在一些新发现的拓扑材料体系中蕴含了丰富的新物理，同SmB6中的关联拓扑行为表现出了较强的关联性。例如以MnBixTey为代表的本征磁性拓扑绝缘体的出现，实现了本征拓扑材料的高温反常量子霍尔效应(QAHE)[118]。而在Eu掺杂的SmB6中发现的反铁磁与拓扑相的共存，是否可以同样在10 K左右可测到QAHE？这对于论证SmB6中的表面态的拓扑性质非常具有启发性。此外，在一些非f电子的关联拓扑体系，例如Kagome格子拓扑材料Mn3Sn中观测到了由Kondo共振所产生的隧穿谱法诺效应(Fano effect)，该现象也曾经在SmB6中被观测到[119]。且Mn3Sn被认为是一个平带体系，因此也引出了一个长久以来的疑问，在具有平带的非f电子体系中是否存在近藤相互作用，甚至是Kondo晶格的形成？因此，SmB6除了它的非平庸拓扑性质，还有更为丰富的物理值得继续挖掘和探讨，相信对SmB6的深入研究也会对上述问题在内的诸多问题带来更多的启发性观点。

致 谢

本文感谢国家自然科学基金委 (U2032156，12004071)，江苏省自然科学基金委(BK20200348)，江苏特聘教授和江苏省双创团队计划的资助支持。