基于机载高光谱数据的田间尺度胡敏酸含量估算
郭 晗,徐敏贤,徐飞飞,罗 明,陆 洲,*,张 序
(1.苏州科技大学 环境科学与工程学院,江苏 苏州 215009;2.中国科学院 地理科学与资源研究所,北京 100101;3.中亿丰建设集团股份有限公司,江苏 苏州 215131)
作为衡量土壤生产力的重要指标,土壤肥力的高效监测受到学者的广泛关注。高光谱技术的快速发展,为土壤组分空间量化带来新的手段。卫星遥感具有飞行高度高、扫描带宽大的特点,能够在短时间内获取大面积的光谱信息[1],现已在区域土壤肥力监测中得到广泛运用。Meng等[2]、马驰[3]、齐雁冰等[4]分别基于不同卫星的高光谱数据,展开区域尺度的土壤组分高光谱估算,均取得了较好的预测效果。然而,当前全世界范围内的农业生产模式仍以家庭农场为主,生产规模难以达到区域尺度[5];因此,基于大范围尺度建立的土壤肥力预测模型并不适用于以家庭农场为主的生产单元内的土壤肥力预测。相较于区域尺度上的土壤肥力监测,田间尺度上的土壤肥力监测更适应于当前农业的发展需求。
进入21世纪以来,无人机(UAV)遥感技术迅速发展。相较于卫星遥感,无人机遥感在光谱分辨率、操作灵活性上均有大幅提高,并已逐渐应用于田间尺度上的土壤光谱实时获取[6]。当前,基于无人机高光谱的土壤肥力估算多围绕土壤中含量较高的有机质展开。Peón等[7]利用机载高光谱扫描仪(AHS)构建山区植被覆盖区数据源,建立起可对土壤有机质进行高效监测的多元线性回归预测模型。秦凯[8]通过重建机载高光谱数据,展开岩石矿物和土壤有机质的信息提取算法研究,建立了高效估算有机质含量的模型。张东辉等[9]利用CASI-1500航空高光谱成像系统,在380~1 050 nm光谱范围内预测了我国建三江区域的土壤肥力,对有机质含量的估算误差为5.25%,预测效果理想。王磊[10]采用Cubert UHDl85机载高速成像光谱仪对耕地土壤有机质含量与光谱响应规律进行测定,为利用无人机高光谱估算耕地土壤肥力提供了方法借鉴。尽管针对土壤有机质含量的高光谱估算方法已趋于成熟,但由于土壤有机质组成复杂,且会因内部碳氮比变换,以及外部水热状况、通气状况、土壤酸碱性的变化而发生矿化、腐殖化反应;因此,不同环境土壤有机质对光谱的响应差异较大[11],有机质估算模型的普适性也较差。相较于有机质,胡敏酸成分单一,理化性质稳定,不易受环境影响,可与光谱建立稳固响应[12]。同时,胡敏酸对土壤结构和土壤中有机碳的变换均具有重要作用[13]。因此,对胡敏酸含量进行高效监测,对于精准农业的发展来说亦具有重要的应用价值。
本文以无人机高光谱系统为数据源,以南方水稻土为研究对象,在田间尺度上开展胡敏酸含量的估算研究。主要研究内容包括:(1)首先,对原始光谱进行去除包络线(CR)、倒数(IR)、对数(LR)、一阶导数(FDR)、二阶导数(SDR)、倒数&一阶导数(IFDR)、对数&一阶导数(LFDR)、倒数&对数(ILR)8种变换,筛选可增强光谱敏感性的最佳单波段变换方法。接着,对原始光谱和经单波段变换后的光谱进行归一化处理,构建归一化光谱指数(NDSI),削弱不同波段之间的干扰,增强光谱与土壤胡敏酸含量间的复杂联系。(2)对归一化光谱指数与胡敏酸含量进行相关性分析,剔除冗余光谱,定位胡敏酸含量响应归一化光谱指数的准确位置。(3)建立多元线性回归(MLR)、偏最小二乘(PLSR)、反向神经网络(BPNN)、支持向量机(SVM)等估算模型,综合分析决定系数(R2)、均方根误差(RMSE)、相对分析误差(RPD),对模型性能做出评价,从而筛选出最佳光谱变换与建模方法的组合,为实现田间尺度上的胡敏酸含量高光谱监测提供方法借鉴。
1 材料与方法
1.1 研究区概况
研究区位于江苏省苏州市震泽镇(图1-A),地理坐标在120°30′56.31″~120°31′11.30″E,30°56′48.53″~30°57′2.07″N。该地年降水量在800~1 500 mm,气候温暖、湿润[14],属亚热带湿润季风气候区。土壤类型以粉砂质黏壤为主,具有颗粒细小、孔隙度高的特点[15],有利于降水入渗,且底土层的黏壤或粉砂黏壤对入渗降水有拦截作用,保水保肥性好。研究区耕地类型以水田为主,水稻是主要的种植作物[16]。
1.2 土样采集与胡敏酸含量测定
去除道路、水渠等非农田区域,通过ArcMap 10.6软件的Create Finshnet工具,绘制边长40 m的网格,以每个网格中心为采样点,在整个研究区内均匀布设45个采样点。
实际采样时,将45个采样点的坐标导入佳明ETrex229X型户外手持GPS导航仪中,通过5点采样法(以每个点的坐标为中心,做边长40 m的正方形,以中心点和正方形的4个顶点为采样点)采集0~15 cm的表层土壤1 kg,充分混合后作为一个土样,避光保存。
胡敏酸含量测定,采用国际腐殖酸协会推荐的方法,结合Rosa等[17]、李丽等[18]的研究,简述如下:加入0.05 mol·L-1的NaOH,超声振荡30 min提取,将提取液于4 500 r·min-1条件下高速离心10 min,重复提取3次;然后,加入1 mol·L-1的HCl溶液,调节pH值至1~2,收集沉淀;再用0.1 mol·L-1KCl溶解沉淀,去除胶体杂质,收集上清液,向上清液中加入1 mol·L-1的HCl,调节pH值至1~2,再次收集沉淀,称量,测算土壤胡敏酸含量。
向SPSS 22软件导入采样点胡敏酸含量,根据含量分布,将32个样本划分为建模集、13个样本划分为验证集(图1-B)。不同样本集合在空间分布上较为均匀。
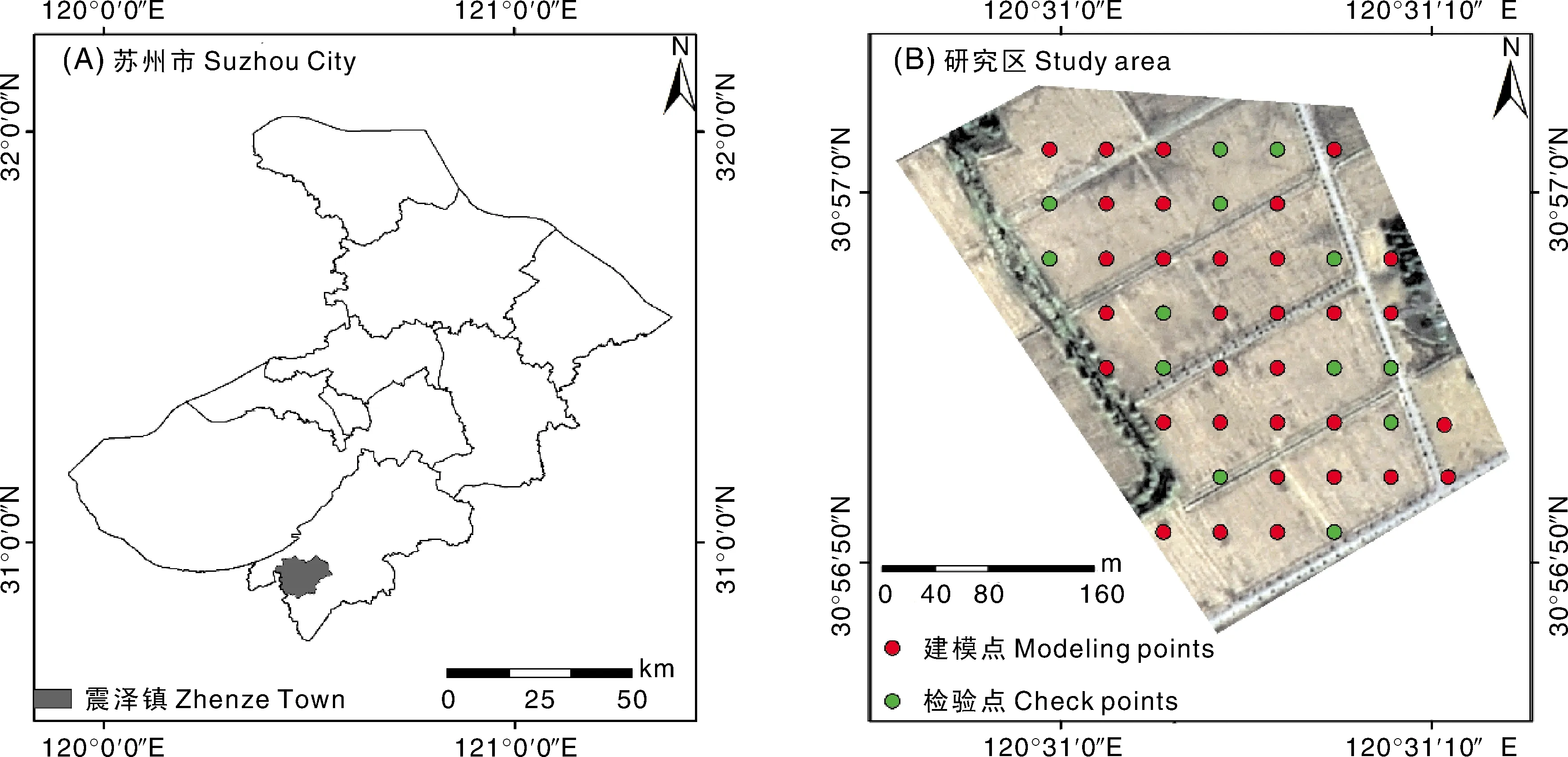
图1 研究区位置
1.3 高光谱数据采集与处理
1.3.1 高光谱数据采集
利用四川双利合谱科技有限公司自主研发的GaiaSky-Mini2-VN高光谱成像系统获取研究区的高光谱数据。GaiaSky-Mini2-VN机载成像传感器的参数如下:光谱范围396~1 000 nm,光谱分辨率3.5 nm,探测器全幅像素1 920 pixel×1 440 pixel,镜头焦距23 mm,图像最大分辨率1 920 pixel×2 080 pixel,图像默认分辨率960 pixel×1 040 pixel,Bin方式包括1 440通道、720通道、360通道、176通道,空间分辨率(镜头焦距23 mm、飞行高度300 m)可达0.12 m,扫描速度为9 s·通道-1。该系统克服了中小型无人机搭载推扫式高光谱相机工作过程中由于无人机系统振动而引起的成像质量差的问题,可与大疆Mpro 600无人机(深圳市大疆创新科技有限公司)完美结合,完成目标识别、地面物体遥测等功能。
为削弱非必要环境因素对高光谱数据的影响,于2020-01-22获取高光谱数据。此时,正值水稻休耕期,研究区地表裸露。当天,天气晴朗,风量小。设置飞行高度300 m,旁向覆盖率70%,南北方向飞行2个架次,空间分辨率达到0.12 m,光谱分辨率达到3.5 nm。
对于获得的高光谱数据,先利用GaiaSky-Mini2-VN高光谱成像系统自带的数据处理工具Spec View对60景影像进行镜头校正、反射率校准、大气校正处理,再利用HiSpectral Stitcher工具实现研究区影像拼接。通过Envi 5.3软件的ROI Tool工具提取采样点反射率。
1.3.2 高光谱数据处理
高光谱数据具有精度高、信息量大的特点。为去除冗余信息、增强波段之间的微弱关联、减弱模型的复杂性[19],首先对176个波段45个采样点的原始反射率分别进行CR、IR、LR、FDR、SDR、IFDR、LFDR、ILR等8种单波段变换。
在单波段变换的基础上,为深度挖掘光谱与土壤组分之间的复杂关系,在Matlab2018(a)软件中对未经变换的原始光谱和经单波段变换后的光谱进行两两组合,构建NDSI。计算公式如下。
(1)
式(1)中:VNDSI为NDSI的值;λ1、λ2为任意2个波段(经单波段变换或不经变换)的光谱,λ1≠λ2。
1.4 胡敏酸含量估算模型的建立与评价
1.4.1 特征光谱提取
特征光谱的准确筛选是建立优质模型的关键。高光谱数据经处理后,形成的NDSI数据量很大。为提高建模效率,增加模型可比性,对冗余光谱进行剔除,并对模型的输入变量进行统一。在Matlab2018(a)软件中通过Corrcoef函数[20]计算NDSI与胡敏酸含量的相关性系数,并对其排序,筛选出响应胡敏酸含量变化强烈的光谱,作为建模的特征光谱。
1.4.2 模型建立
结合已有研究[1,21-24],选取MLR、PLSR构建胡敏酸含量估算的线性模型,选取BPNN、SVM构建胡敏酸含量估算的非线性模型。
在SPSS 22软件中构建MLR模型。考虑到光谱之间可能存在的共线性问题,选用后退法筛选联合作用强的自变量,剔除对因变量影响不显著的自变量。以95%作为变量误差表征级别,对变量进行选入和剔除[25],构建基于原始光谱及其8种单波段变换的预测模型。
在Matlab2018(a)软件中构建PLSR模型。翁永玲等[26]研究表明:PLSR在土壤组分高光谱估算中能有效地减少光谱维数,揭示最大组分含量变化的主控因子,且建立的模型有很好的稳定性。但也有研究表明:当土壤类型增多时,PLSR表现不出较好的预测效果[27]。本文是在田间尺度上对土壤组分含量进行预测,土壤类型单一,推测在建立PLSR模型时不存在上述问题。
在Matlab2018(a)软件中构建BPNN模型。BPNN是一种按照误差逆向传播算法训练的神经网络,是目前应用最广泛的神经网络[28]。研究表明,BPNN能高速寻找优化解,充分逼近复杂的非线性关系[29]。本文在BPNN模型训练中,通过输入变量选择来提高模型质量,从而充分发挥神经网络的优势。
在Matlab2018(a)软件中构建SVM模型。SVM是一种以非线性映射为理论基础的小样本机器学习方法。SVM的精髓,是利用核函数对数据进行高效分类。径向基核函数具有良好的分类功能,是最常用的核函数[30]。本文选用SVR_Epsilon模型、高斯径向基核函数寻求模型最优解。
1.4.3 模型评价方法
利用建模集的R2、RMSE和验证集的R2、RMSE、RPD来评价模型性能。R2值越大,说明模型拟合待测组分的能力越强。RMSE值越小,说明模型的估算精度越高。RPD值小于1.2时,模型不具可靠性;RPD值大于1.4时,模型具有可靠性;RPD值大于2时,模型可用于土壤组分的估算[29]。
2 结果与分析
2.1 土样测定结果
将土样中胡敏酸含量的测定结果整理于表1,样本的值域大,变异强度中等,建模集、验证集的平均值相近。可见,建模集、验证集具有较好的代表性,样本划分较为合理。

表1 土壤样本的胡敏酸含量特征统计
2.2 光谱变换结果
以波段1为x轴,波段2为y轴,绘制基于原始光谱(RAW),和经CR、IR、LR、ILR、FDR、SDR、LFDR、IFDR变换光谱构建的NDSI(分别简记为NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-ILR、NDSI-FDR、NDSI-SDR、NDSI-LFDR、NDSI-IFDR)分布图(图2),色棒的数值表示NDSI数值。

NDSI,归一化光谱指数。A,原始光谱;B,去除包络线(CR);C,倒数(IR);D,对数(LR);E,一阶导数(FDR);F,二阶导数(SDR);G,倒数&一阶导数(IFDR);H,对数&一阶导数(LFDR);I,倒数&对数(ILR)。下同。
其中,NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-ILR在全波段遵循有序的数值变换规律(由小到大或由大到小),相邻光谱的NDSI差距小,特征光谱信息不突出。相反地,NDSI-FDR、NDSI-SDR、NDSI-LFDR、NDSI-IFDR值在全波段的分布无明显规律性,整体呈绿色,同时存在小面积的突出斑点。结合NDSI色棒来看,斑点处波段的NDSI值与相邻波段的NDSI值相差较大,对胡敏酸的响应敏感。这表示:经过FDR、SDR、LFDR、IFDR变换后的光谱NDSI值能够有效区分冗余光谱和敏感光谱,突出特征光谱信息。其中,FDR变换后的光谱信息最为丰富,这与周倩倩等[22]的研究结果一致。
2.3 特征光谱提取结果与分析
2.3.1 相关性分析
以波段1为x轴,波段2为y轴,绘制NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-ILR、NDSI-FDR、NDSI-SDR、NDSI-LFDR、NDSI-IFDR与胡敏酸含量的相关性系数分布图(图3)。其中,NDSI-RAW、NDSI-IR、NDSI-LR、NDSI-ILR与胡敏酸含量的相关性系数在全波段范围内分布较为均一,相关性系数差距不大;而NDSI-FDR、NDSI-SDR、NDSI-LFDR、NDSI-IFDR与胡敏酸含量的相关性系数在全波段分布不均匀,相关性系数大的区域和相关性系数小的区域区分明显,相关性信息丰富。这与NDSI-FDR、NDSI-SDR、NDSI-LFDR、NDSI-IFDR在全波段的分布情况对应,说明这些变换能够弱化无关组分,突出特征光谱。

图3 原始光谱和经不同变换后光谱的归一化光谱指数与胡敏酸的相关性系数在全波段的分布
经相关性分析,NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-FDR、NDSI-SDR、NDSI-IFDR、NDSI-LFDR、NDSI-ILR与胡敏酸含量的最大相关性系数分别于(897.6,908.6)(分别对应于x,y坐标,下同)、(512.6,515.9)、(904.9,908.6)、(904.9,908.6)、(470.1,757.8)、(670.8,963.8)、(542.3,558.9)、(897.6、908.6)、(479.8、694.9)处取得。其中,导数及其组合变换(FDR、SDR、IFDR、LFDR)后的归一化光谱指数与胡敏酸含量的最大相关性系数均高于0.500(图4),相关性大。这与导数及其组合变换后的光谱能够突出特征光谱信息密切相关。其中,NDSI-FDR与胡敏酸含量的最大相关性系数为0.557,相较NDSI-RAW提高0.115,可作为增强光谱敏感性的首选方法;而NDSI-CR与胡敏酸含量的相关性表现欠佳。
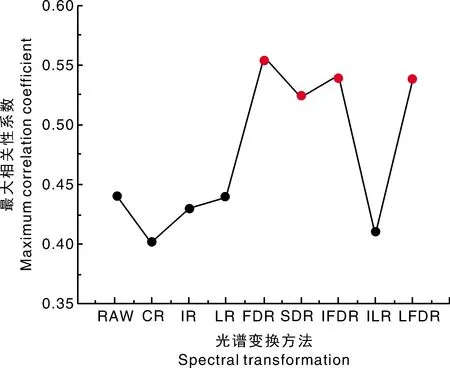
RAW,不变换。下同。
2.3.2 特征光谱分布
基于胡敏酸含量与光谱之间的相关性系数,筛选出胡敏酸与光谱响应强烈的光谱(即特征光谱),绘制特征光谱密度分布图(图5),定位胡敏酸响应光谱的准确位置。结果表明:在396~1 000 nm,有3处特征波段密集区。放大密集区,可将其分别定位到480~550 nm与510~570 nm组合处、730~790 nm与740~800 nm组合处、880~930 nm与880~930 nm组合处。为提高建模效率,剔除特征波段密集区外的光谱,将特征光谱密集区用作后续建模的输入变量。

图5 特征光谱在396~1 000 nm范围内的分布
2.4 建模结果与分析
基于NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-ILR、NDSI-FDR、NDSI-SDR、NDSI-LFDR、NDSI-IFDR主要特征光谱,分别利用MLR、PLSR、BPNN和SVM建立估算胡敏酸含量的模型,记录其在建模集和验证集上的R2、RPD、RMSE值(图6),并根据上述参数对模型进行初步评价。基于BPNN建立的预测模型的R2(含建模集和验证集)高于MLR、PLSR、SVM,说明BPNN预测模型的精度较高,拟合胡敏酸含量的能力较强。

A,多元线性回归(MLR)模型;B,偏最小二乘(PLSR)模型;C,反向神经网络(BPNN)模型;D,支持向量机(SVM)模型。建模集上的决定系数;验证集上的决定系数;RPD,相对分析偏差。
利用MLR、PLSR、BPNN、SVM建立的模型中,RPD值大于1.4的数量分别为6、1、3、3个。其中,利用MLR建立的预测模型的整体可靠度高于BPNN、PLSR、SVM。但是,模型性能是精度、可靠性、稳定性的综合体现。为此,将RPD值大于1.4的预测模型的评价参数(R2、RPD、RMSE)整理于表2,做进一步分析,以筛选出最佳估算模型。横向对比发现:MLR模型建模集和验证集的R2均较低,模型拟合性不佳。基于NDSI-IFDR建立的PLSR模型的RPD值达到了1.620,模型具有一定的可靠性,但是建模集和验证集上的R2分别为0.734和0.212,建模精度、验证精度相差较大,模型存在过拟合现象。同PLSR建模结果相同,SVM模型建模集上的R2明显高于验证集,说明该模型也存在过拟合现象,且建模集和验证集上的RMSE相差大,模型稳定性差。RPD值大于1.4的3个BPNN模型,其建模集和验证集上的R2均处于较高水平,且RMSE值较为接近,说明模型性能较好。其中,基于NDSI-LFDR建立的BPNN模型,建模集和验证集上的R2分别为0.916和0.805,RMSE分别为0.799、1.107,模型精度最高,稳定性好,且RPD大于2,说明该模型可以用于土壤胡敏酸含量估算。

表2 RPD值大于1.4的模型参数
3 讨论
3.1 利用高光谱估算胡敏酸含量的可行性
本文共筛选出3处特征波段密集区,其中,480~550 nm与510~570 nm组合处、730~790 nm与740~800 nm组合处的特征波段与郭晗等[31]在土壤有机质含量预测中筛选出的有机质归一化光谱指数敏感区域吻合。可见,有机质、胡敏酸对光谱的响应存在一定的联系。洪永胜等[32]指出,光谱对有机质的响应是由胡敏酸引起的。理想情况下,有机质、胡敏酸的特征波段应该完全吻合。但本文结果表明,880~930 nm与880~930 nm组合处是胡敏酸独有的特征波段密集区。这说明,本研究筛选出的特征波段更全面。这与有机质、胡敏酸的物理、化学稳定性密切相关。胡敏酸组成相对单一,物理化学性质稳定,能够不受环境影响在土壤中停留80~3 000 a,对光谱的响应准确、稳定。有机质含量、内部组成与周围环境显著相关[33-35],时间、空间稳定性差。相比之下,本文直接以胡敏酸为光谱响应组分筛选出的特征光谱更加可靠、全面,建立的土壤胡敏酸含量估算方法也更具可行性。
3.2 单波段变换与双波段变换组合的优势
单波段变换能够有效增强光谱与待测组分之间的相关性,但是待测组分不仅与单波段存在联系,还与双波段、甚至多波段存在复杂的关系。本文在对光谱进行单波段变换的基础上,采用归一化的方法,将原始光谱和变换后的光谱两两组合,构建了包含双波段光谱信息的NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-FDR、NDSI-SDR、NDSI-IFDR、NDSI-LFDR、NDSI-ILR。相关性分析中,不同归一化光谱表现出不同的效果,导数及其组合处理后的NDSI值(NDSI-FDR、NDSI-SDR、NDSI-IFDR、NDSI-LFDR)在全波段范围内分布不均匀,大量指数值位于NDSI值域中位数附近,少量指数值位于值域最大值或最小值附近,特征光谱十分突出。相比之下,NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-ILR分布较为均匀,特征光谱与背景噪声难以区分。与此对应,导数及其组合变换的NDSI在与胡敏酸含量的相关性分析中也取得较高的相关性系数,这与卢艳丽等[36]研究结果一致。其中,以NDSI-LFDR作为建模输入变量时,建模效果最佳。这是由于单波段变换与双波段变换的合理组合能够充分综合不同变换的优势,最大化诠释光谱信息[37]。在以后的研究中,还需加强其他单波段变换与双波段变换方法组合的探索,增强光谱诠释信息的能力。
3.3 BPNN估算胡敏酸的优势
利用BPNN建立的胡敏酸估算模型具有较高的建模精度和估算精度,明显优于MLR、PLSR、SVM。这与Tian等[38]在土壤有机质含量预测中的表现一致。总体来说,BPNN模型的学习能力强,能够挖掘复杂交互的非线性关系[39]。但是,BPNN是“黑箱”操作模式,难以了解输入与输出之间的复杂关系,为了追求高精度,常会导致过拟合。以NDSI-RAW、NDSI-CR、NDSI-IR、NDSI-LR、NDSI-ILR、NDSI-SDR为输入变量建立的BPNN估算模型中,出现了高精度与低可靠性并存的现象。Meng等[2]研究发现,选择最适变换光谱与BPNN结合,能够有效地提高建模效果。本文以NDSI-LFDR、NDSI-FDR、NDSI-IFDR作为BPNN输入变量时,建立的模型兼具高精度、高稳定性、高可靠性。
在实际应用中,计算时间也是评价模型的重要指标。虽然BPNN建模效果最佳,但也存在着计算时间长、对计算设备性能要求高的弊端。在以后的研究中,需要将计算时间纳入模型评价体系中[40-41]。
4 结论
本文针对当前土壤组分高光谱估算面积大、模型难以在地块应用的问题,结合当前精准农业发展需求,针对理化性质稳定、不易受环境影响的胡敏酸的含量进行估算。以机载高光谱为数据源,以田间尺度为研究范围,利用MLR、PLSR、BPNN、SVM建立胡敏酸含量的高光谱估算模型。结果表明:导数变换在加强机载特征光谱与胡敏酸的联系、去除冗余信息上表现优秀。在众多变换中,导数变换与对数变换的组合能够充分结合二者诠释信息的优势,在突出光谱特征方面效果最明显。基于特征光谱建立的模型中,BPNN的建模精度明显高于MLR、PLSR、SVM。其中,基于NDSI-LFDR建立的BPNN预测模型在建模集和验证集上的R2分别为0.916、0.805,RMSE分别为0.799、1.107,RPD为2.189,建模效果最佳。本文对田间尺度胡敏酸含量估算的研究,可为精准农业土壤组分精细化、高效化监测提供参考。

