分级围岩下充填滞后时间优化及数值分析
李志海,刘建博,闫 刚,王 灵,付佳杰,孙鸣阳
(1.招金矿业股份有限公司蚕庄金矿,山东 招远 265414;2.北京科技大学 土木与资源工程学院,北京 100083)
地下矿山开采过程中,及时对采空区进行充填,能有效提高矿体回采过程的安全性,在矿体开挖后,确定合理充填滞后时间,可以显著提高矿体开采效率。岩体的蠕变特性[1-2]是影响充填滞后时间确定的主要因素,自GRIGGS[3]对灰岩、砂岩和页岩等岩石进行蠕变试验以来,众多学者针对岩石蠕变特性进行了广泛研究,所采用的研究手段包括理论推导、室内试验以及数值模拟,并取得了丰硕的研究成果。
在理论推导方面,曹树刚等[4]参考西原正夫模型,结合弹性体与改进的黏滞模型,推导出能表征岩石三阶段的改进西原正夫模型。王来贵等[5-7]以改进的西原正夫模型为基础,利用岩石全过程应力-应变曲线与蠕变过程中参数的对应关系,建立参数非线性蠕变模型,更加准确地描述了岩石蠕变三阶段变形。马白虎[8]基于RLW-2000型微机伺服岩石三轴流变仪得到的泥岩流变实验数据,对其蠕变曲线特征进行分析,并结合岩石的力学特性,定义了一种能反映岩石加速蠕变破坏特征的非线性函数。鲜学福等[9]提出采用五元黏弹塑流变模型来描述煤体的蠕变特征,并考虑瓦斯的作用,得到了含瓦斯的煤蠕变状态方程,并以此预测出煤体蠕变失稳的时间。许龙星等[10]基于改进的西原正夫模型,给出了平面应力状态下巷道煤岩体蠕变失稳时间,从而确定了煤体开挖后最佳支护时间。在室内试验和数值模拟方面,胡波等[11]针对大安山煤矿+550 m水平西二石门围岩蠕变变形严重问题,采用室内蠕变试验与理论分析方法,研究了应力水平与蠕变速率之间的关系,确定了起始蠕变应力阈值。王青元等[12]在岩石蠕变试验的基础上,加入冲击扰动因素,研究了开采扰动诱发岩石加速失稳破坏机理,从能量角度分析了蠕变岩石在冲击扰动下的破坏规律。辛亚军等[13]对红砂岩样进行高应力区峰后单轴压缩蠕变试验,研究了红砂岩峰后瞬时应变、蠕变应变与应力水平的关系,红砂岩峰前峰后蠕变关联特性,并确定了红砂岩蠕变破坏机制。张乃烊等[14]研究了软岩注浆结石体的蠕变特性,分析不同荷载水平、不同含水条件对泥质页岩注浆结石体蠕变特性影响。胡光辉等[15]基于三维颗粒流程序,从细观角度探究了脆性岩石的蠕变失稳过程及失稳机理。
上述学者对岩体蠕变稳定研究大多侧重于用理论推导来描述岩石蠕变变形过程以及从室内试验的角度来描述蠕变破坏机理,而对充填采矿法中不同等级围岩中采空区的合理充填时间的研究却鲜有涉及。因此,本文在前人大量研究的基础上,利用FLAC3D软件针对蚕庄金矿不同质量等级围岩在矿体开挖后的充填滞后时间进行数值模拟,合理确定充填滞后时间,为矿山安全高效开采提供理论依据。
1 矿区概况
蚕庄金矿地处焦家断裂带北段,大部分为第四系松散沉积物覆盖,岩浆岩广布,断裂构造发育。矿区主要赋存矿体为1#矿体,且矿体较为集中,呈脉状,赋存于破碎蚀变带内的黄铁绢英岩化碎裂岩及黄铁绢英岩化花岗质碎裂岩中,并且夹有少量绢英岩化碎裂岩及糜棱岩等。
本次开采范围是采矿权范围内-860 m水平以上矿体,采矿方法为上向水平沿脉进路分层尾砂胶结充填法。由于围岩质量等级差异大,因此,分别考虑在不同岩体参数条件下,采场开挖后立即充填采场、滞后一天充填采场、滞后两天充填采场、滞后三天充填采场,计算在不同时间段下充填采场时采场的应力、变形情况。
2 蠕变分析
采场开挖后,巷道会产生大变形现象,蠕变分析(图1)可有效揭示变形的机理及其影响因素[16]。以往的蠕变模型只能描述衰减蠕变过程,因此本文利用改进的西原正夫模型并根据前人对蠕变特性的研究[17-18]确定合理的充填时间。

图1 改进的西原模型及其蠕变曲线Fig.1 Modified Nishihara model and its creep curves
图1(a)中,E1为模型的弹性模量,GPa;E2为模型的黏弹性模量,GPa;η1、η2为模型的黏性系数。根据岩石全应力-应变曲线,E2随时间的变化而变化。图1(b)中σf为岩石的长期强度;σ0为模型所处蠕变应力,GPa。此次研究,仅考虑σ0>σf下,岩石可以发生全过程蠕变状态。因此,在常应力(σ=σ0)作用下,模型的应变可表示为(1)式。
(1)

(2)
模型的应变加速度见式(3)。
(3)

采场开挖后,由于充填时间的不同,会导致围岩的变形出现较大差异。结合公式和蠕变曲线,当围岩处于初始蠕变阶段,进行采场的充填,会取得较好的支护效果,能够最大限度地控制围岩的变形,对围岩的稳定性能够进行较好的控制;当围岩处于加速蠕变阶段,由于围岩的变形较大,随时会出现岩石的失稳,危险性较大,此时进行充填效果不太显著。因此,需要研究采场在开挖之后其蠕变情况,以便准确确定充填时间,从而使采场稳定性得到控制。
3 矿体开采充填滞后时间模拟分析
3.1 数值模型构建
基于数值模拟技术,将处于不同质量等级岩体的矿体开挖后,对围岩所受应力、变形进行分析,并借助改进的西原正夫模型,确定不同岩体质量等级下矿体开挖后合理充填滞后时间。应用FLAC3D软件进行矿区采场模型建立,模型设计采场横截面为5 m×4 m,设计采深800 m。整个模型尺寸为80 m×40 m×70 m,共253 257个节点、240 800个单元。根据现场情况,创建围岩1、围岩2、巷道三大组模型,模型如图2所示。
根据矿体实际赋存条件,分别考虑在不同岩体参数条件下,采场开挖后立即充填采场、间隔一天充填采场、间隔两天充填采场、间隔三天充填采场,计算在不同时间段下充填采场时采场的变形情况。监测点主要设置两个,分别布置在采场的顶板和边帮,分为1号和2号监测点,具体监测位置如图2所示。

图2 数值模型构建及监测点Fig.2 Construction of numerical model and monitoring points
3.2 岩石力学参数及初始地应力确定
根据蚕庄金矿现有地质资料,可知开采区域岩体等级主要为Ⅳ级,但其他区域相对围岩质量等级有所不同。因此,针对不同质量等级岩体分别选取相应的力学参数,其主要力学参数按照岩石力学实验结果选取,岩体主要力学参数如表1所示。

表1 岩体基本力学参数
结合现场实测数据得到应力随深度的回归方程,如式(4)所示。进行初始地应力场的施加,并设置重力加速度9.8 m/s2,生成初始应力场。
(4)
3.3 应力变化结果分析
图3为不同等级岩体充填滞后时间应力变化规律图。首先,Ⅲ级岩体,在不同充填滞后时间内边帮受力均大于顶板受力,因此,在开采过程中应着重观察边帮变形情况,避免因边帮受力过大产生片帮等事故,随着充填滞后时间的增长,边帮和顶板的受力均缓慢增大,由于岩石质量较好,其蠕变速率较小,矿体开挖后充填滞后时间相对于其他两级质量岩体较长;Ⅳ级岩体,同Ⅲ级岩体应力变化规律相似,但其顶板受力大于边帮受力,且蠕变速率大于Ⅲ级岩体蠕变速率,在此受力状态下会较早进入稳定蠕变阶段,因此Ⅳ级岩体的充填滞后时间超前于Ⅲ级岩体的充填滞后时间;Ⅴ级岩体,顶板受力大于边帮受力,且其在采场开挖后,随着充填滞后时间的增长,顶板和围岩受力基本保持在固定值,在此受力状态下,其岩体变形速率显著大于Ⅲ级、Ⅳ级岩体。因此,对于Ⅴ级岩体而言,应该做到矿体回采后尽早充填采空区,最大限度确保采矿安全。同时,对于Ⅳ级、Ⅴ级岩体,在开采过程中,要注意顶板变形情况,避免产生冒顶等事故。

图3 应力变化Fig.3 Stress changes
3.4 位移变化结果分析
图4为采场开挖后顶板和两帮位移随时间变化规律图,与不同等级岩体受力相对应,除Ⅲ级岩体两帮位移值大于顶板位移值外,Ⅳ级、Ⅴ级岩体位移值均是顶板位移大于两帮位移,且由于岩体质量等级不同,Ⅲ级、Ⅳ级、Ⅴ级岩体位移值相应增大。通过位移曲线可知,不同等级围岩在采场开挖后立即进行充填均可有效抑制围岩变形。在矿体开挖24 h内,不同等级岩体均处于初始蠕变状态,但随着岩石质量等级的变差,位移变化速率逐渐增大。在矿体开挖48 h内,Ⅲ级、Ⅳ级岩体依然处于初始蠕变状态,而Ⅴ级岩体已经处于稳定蠕变状态。因此,结合受力情况,对于Ⅴ级岩体充填滞后时间,应尽量控制在20 h内,最迟不应该超过30 h,这样可有效抑制围岩变形。在矿体开挖48 h至72 h,Ⅲ级处于初始蠕变状态,其所受应力及位移变化速率逐渐减小,即将进入稳定蠕变状态,Ⅳ级岩体进入稳定蠕变状态,但由于岩体质量较差,其所受应力值还在逐渐增大,对于Ⅳ级岩体充填滞后时间应尽量控制在50 h内,最迟不应超过60 h。由于Ⅲ级岩体质量相对较好,其处于加速蠕变时间也较长,由图4可知,其充填滞后时间尽量控制在72 h内,最迟不应超过80 h。
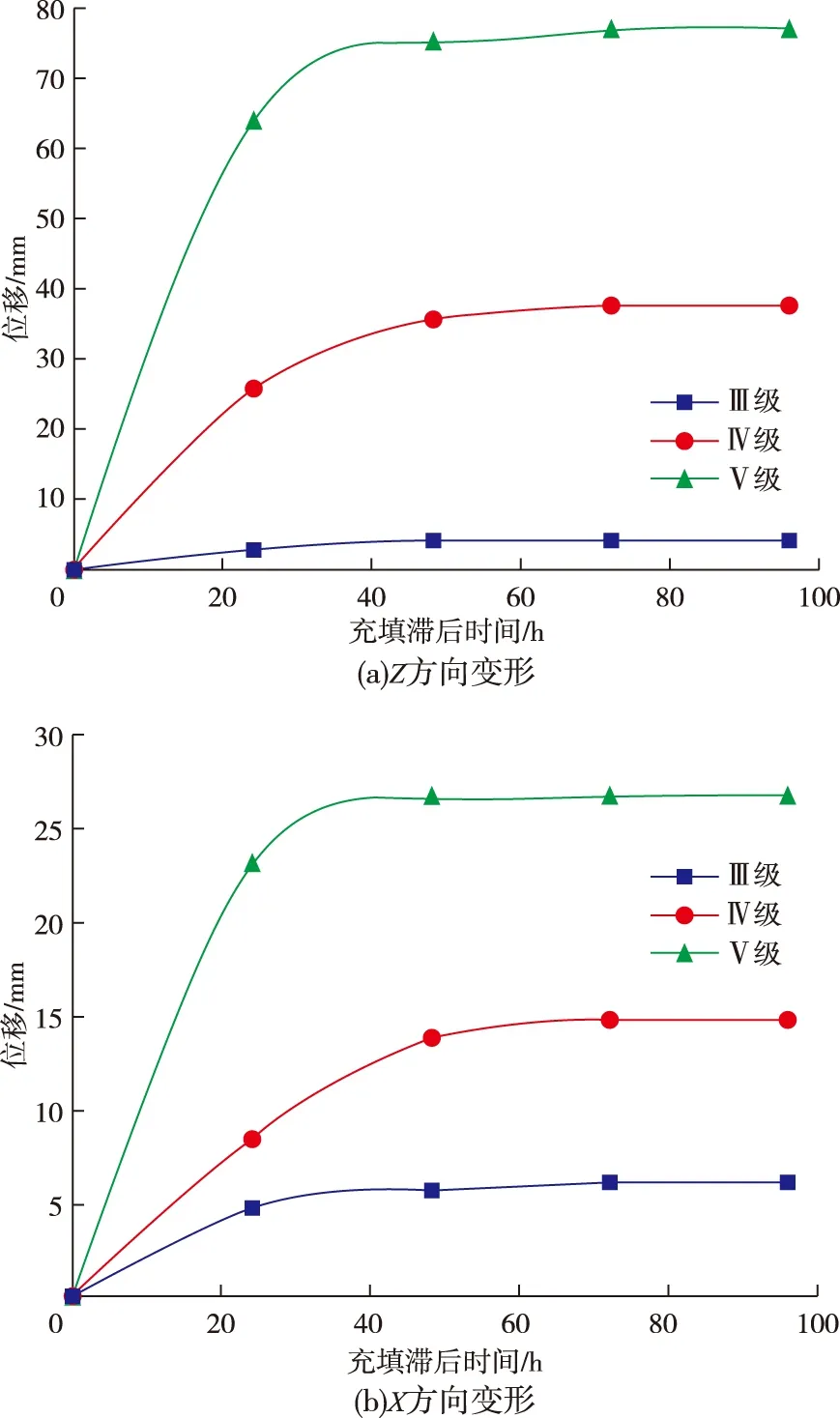
图4 位移变化Fig.4 Displacement changes
4 现场实际监测
4.1 监测设备及方案
本次监测内容包括采场二次应力变化测量、巷道围岩相对位移测量。其中,二次应力变化测量根据现场工程条件选用KSE-Ⅱ-1型钻孔应力计,由压力传感器和数字显示仪(KSE-Ⅱ型钢弦测力仪)组成的分离型钢弦振动式测频数字仪器,压力传感器的钻孔压力枕采用充油膨胀的特殊结构,其结构示意图见图5。

1—包裹体;2—压力枕;3—安装插头;4—导压管;5—压力-频率转换器;6—注油嘴;7—电缆图5 压力传感器结构示意图Fig.5 Structure diagram of pressure sensor
巷道围岩相对位移量测量采用JSS30A型数显收敛计(图6),收敛计的收敛点是在巷道两侧各固定一个测点,使用收敛计测量两测点之间的距离,以得到巷道变形情况。

图6 JSS30A型数显收敛计Fig.6 JSS30A digital display convergence meter
应力变化监测点共设置4个,分别布置在东区-780 m水平采场联络道两帮与-780 m西区采场尽头两端。测点基本情况如表2所示。
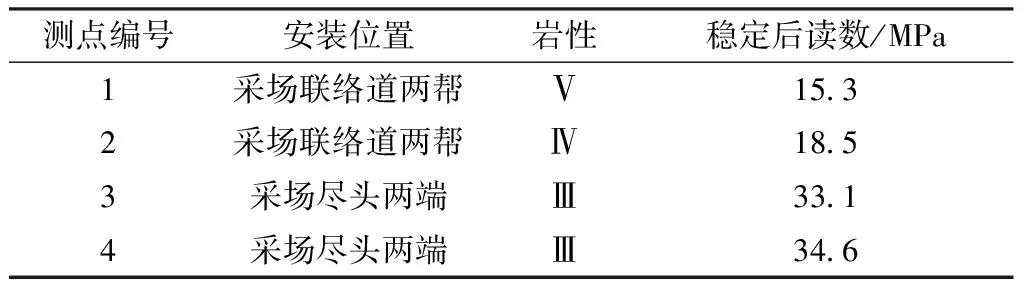
表2 应力测点监测设备数据
位移变化监测点与应力监测点基本一致,主要设置4个监测点,分别布置在应力监测点附近。测点基本情况如表3所示。现场设备安装如图7所示。
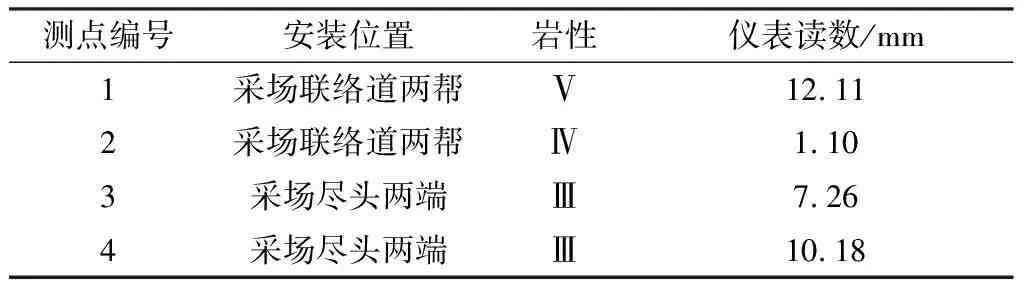
表3 位移测点监测设备数据

图7 监测设备Fig.7 Monitoring equipment
4.2 监测结果分析
在矿体回采完后即进行设备安装,并在前4天内,每天测一遍数据,第5天后每间隔3天测一遍数据。
通过数值模拟分析可知,不同等级围岩下矿体回采完成后,边帮受力值为Ⅲ级岩体>Ⅳ级岩体>Ⅴ级岩体,应力监测装置均位于不同等级岩体采场附近,监测数据具有代表性,可为通过数值模拟确定的充填滞后时间提供依据。通过对前4天监测点测到的数据进行整理,分别得到不同等级围岩应力、位移变化规律曲线,如图8所示。从图8可以看出,1~4号监测点在4天内的应力、位移监测数据发展规律及其大小与数值模拟监测到的数据发展规律及其大小基本吻合,表明通过数值模拟确定的充填滞后时间较为合理,因此应及时按照针对不同等级围岩所设计的充填滞后时间进行充填,确保采场的稳定性。
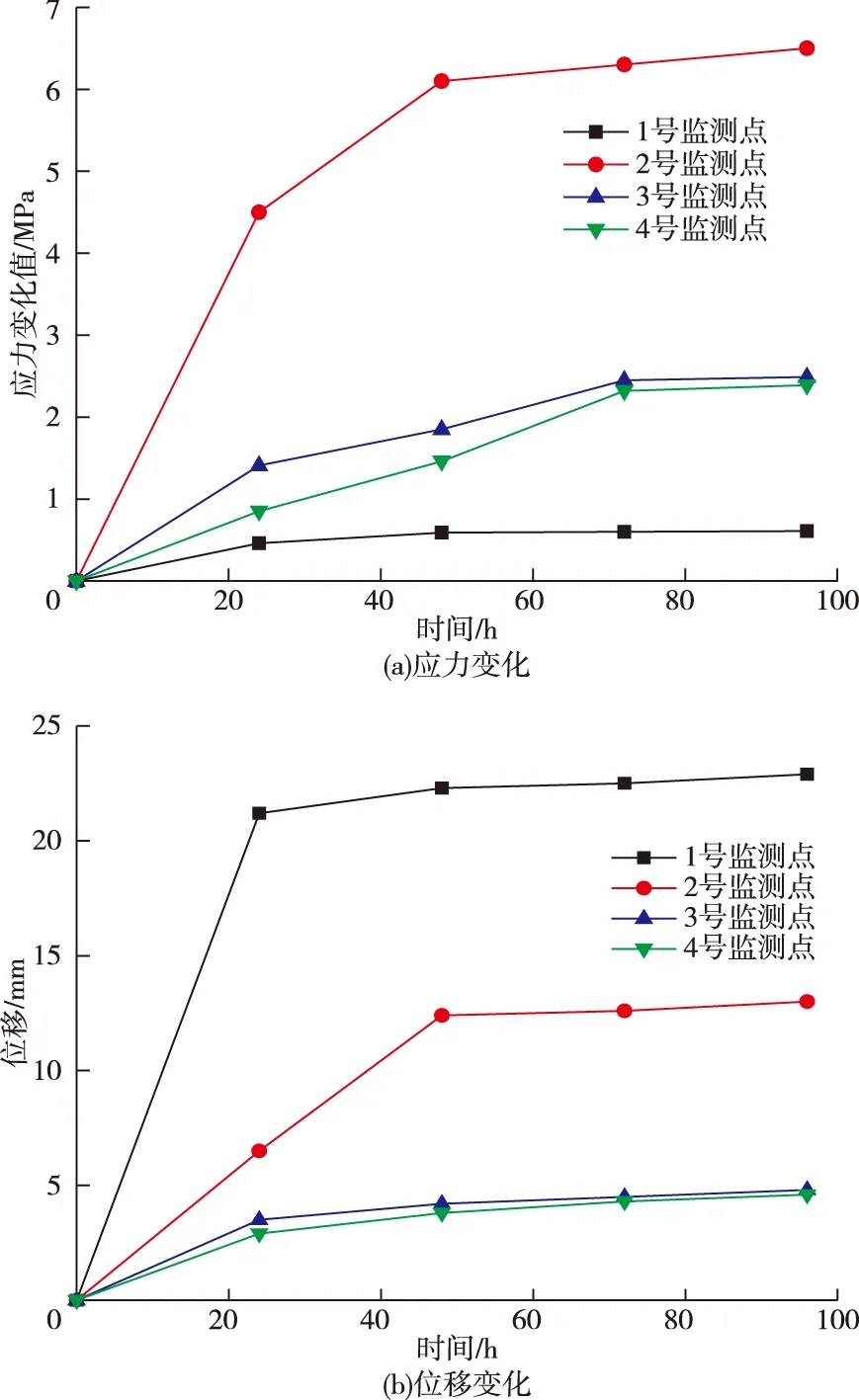
图8 监测数据Fig.8 Monitoring data
5 结论
1)将充填滞后时间与蠕变曲线相结合,利用改进的西原正夫模型,确定蠕变各阶段的蠕变变形量、蠕变速度、蠕变加速度,将采场充填滞后时间转化为蠕变问题来分析,最终确定采场充填滞后时间应在岩体初始蠕变阶段,在此阶段进行采空区充填可有效抑制围岩变形,保证矿体回采安全。
2)Ⅲ、Ⅳ、Ⅴ级岩体在采场开挖后不同时间段进行充填,模拟了开挖后立即充填采场、开挖后滞后一天充填采场、开挖后滞后两天充填采场、开挖后滞后三天充填采场,其变形随时间的变化规律。由模拟结果可知即采即充能使采场的变形达到最小,有效控制采场的变形。
3)结合蠕变理论分析,分别确定不同等级围岩合理的充填滞后时间,Ⅲ级围岩充填滞后时间不应超过80 h,Ⅳ级围岩充填滞后时间不应超过60 h,Ⅴ级围岩充填滞后时间不应超过30 h。
4)通过对现场监测数据进行整理分析,表明数值模拟所确定充填滞后时间具有其合理性,可被同类矿山确保矿体安全回采所借鉴。

