基于进化算法MOEA/D-AU的露天矿多金属多目标智能配矿研究

顾清华，刘思鲁，张金龙

(1.西安建筑科技大学 资源工程学院，西安 710055；2.西安市智慧工业感知计算与决策重点实验室，西安 710055；3.洛阳栾川钼业集团股份有限公司，河南 洛阳 471500)

矿产资源作为我国国民经济的支柱产业，是社会和经济发展的物质基础。随着矿产资源利用率降低，品位不断下降等问题的出现，坚持贫富兼采、合理配矿是提高矿产资源利用率、保证矿石质量的关键。由于露天矿山生产条件的日趋复杂，多目标配矿优化是大型露天矿山研究的趋势，编制科学合理的多目标配矿计划可以有效提高配矿效率，保证矿山企业可持续发展。因此根据矿山实际生产需求，深入研究多目标配矿问题十分有必要。

目前，配矿问题的研究主要集中在计划模型的构建和优化求解算法两个方面。针对计划模型的构建而言，当前研究主要侧重于配矿指标的选取，根据不同矿山的生产需求，将矿石品位偏差、生产成本、总产量作为首要考虑指标的研究居多，其中，王李管等[1]以品位偏差最小为目标函数建立露天矿配矿优化模型，有效解决了多元素多卸矿点配矿而造成的配矿结果粗略等问题；胡乃联等[2]从生产成本的角度出发，以采掘和运输成本最小为目标函数编制露天矿配矿计划，为矿山实际生产提供依据；黄启富等[3]以总利润最大化为目标，动态优化解决企业配矿问题。此外，关于配矿指标的选取，还有对任务量、矿石岩性、氧化率及有害物质方面的研究，其中，柯丽华等[4]根据矿石质量要求，以SiO2等有害物质为约束条件构建配矿数学模型，有效提高了资源利用率；顾清华等[5]考虑影响选矿回收率的氧化率、有害物质等指标，构建基于采选流程的多金属配矿优化模型。

针对优化求解算法而言，主要侧重于数学规划、计算机技术与数学规划相结合和智能优化算法三个方面，其中，侯煜[6]针对某露天矿的实际生产，采用线性规划原理编制配矿的总体策略与简化策略，有效解决传统人工配矿盲目性强且效果较差的问题；刘文博等[7]从供应链角度出发，分析原矿配矿的生产特点，构建露天矿山供应链问题的0-1混合整数规划模型；EIVAZY 等[8]构建了基于混合整数规划的露天矿短期生产计划模型，提高了生产决策效率；井石滚等[9]应用先进的地理信息(GIS)技术、全球卫星定位(GPS)技术及通用无线分组传输(GPRS)技术，设计与实现了露天矿山配矿生产动态管理系统；吴丽春等[10]应用0-1整数规划与三维矿业软件DIMINE相结合对矿山的配矿进行优化，上述研究均为单目标规划，但在实际配矿生产作业中，往往含有多个复杂冲突目标，此时相比于传统求解方法，智能优化算法在求解此类问题上具有明显优势，其中，李宁等[11]针对低品位矿产资源的利用率，构建了多目标配矿优化模型，并提出求解该模型的混合粒子群算法；顾清华等[12]针对露天矿多金属多目标短期配矿问题，建立了基于自适应粒子群算法的配矿优化模型。

综上所述，目前配矿研究已经从单目标向多目标发展，但是对于多目标配矿问题求解而言，大多数研究还是采用理想点等数学方法将多目标转化为单目标，这样并不能在本质上很好地解决多目标优化问题。此外以往研究对选矿因素考虑不充分，仅是将氧化率和有害物质等指标简单地添加到目标和约束中，但实际生产中上述指标对选矿回收率的影响程度不同，需根据矿山实际情况具体分析，才能够显著改善矿石的综合回收率。因此本文针对上述问题，在基于分解的多目标进化算法(Multi-objective Evolutionary Algorithm Based on Decomposition，MOEA/D)的基础上，提出了一种改进的多目标进化算法(MOEA/D-AU)，在求解多目标配矿优化问题上表现优异；根据实际矿山数据，利用随机森林算法建立了综合回收率预测模型，对进化算法求解的多组配矿方案进行筛选，从而得到一个更加符合实际情况的方案。

1 配矿问题描述及模型构建

1.1 问题描述

露天矿山企业的实际生产中，配矿作为企业采选工作的中间环节，将不同品位的矿石进行搭配混匀，增加满足质量标准的矿石产出率。实际生产中，各个出矿点的品位都不相同，即使同一出矿点品位波动也比较大，因此根据各出矿点的品位变化进行合理配矿至关重要。已知各出矿点的实际品位、各受矿点的目标品位、各出矿点到受矿点的运输距离以及各出矿点和受矿点的任务量和最大生产能力。多目标优化配矿问题可以描述为在实现矿石品位偏差最小、岩性配比偏差最小和生产成本最低的情况下，提高配矿效率，此模型的生产成本包括开采成本、运输成本及破碎成本。露天矿多目标配矿模型的部分参数及变量定义如表1所示。

表1 基本符号说明

1.2 模型构建

多目标优化配矿是一个高复杂性、多约束性的问题，模型根据矿山实际配矿情况，综合考虑了矿石品位、生产成本、岩性配比、作业生产能力以及作业任务量等多种约束条件，具体模型构建如下：

(1)

(2)

(3)

式中，目标函数(1)表示矿石品位偏差最小化；目标函数(2)表示采掘、运输及破碎总成本最小化；目标函数(3)表示矿石岩性配比偏差最小化，其中{α，β，γ，…}表示矿石岩性，{μα，μβ，μγ，…}为期望岩性比例，此外模型将属于同一岩性的出矿点归为一类，按不同岩性类别分类排序，即出矿点1到出矿点α全部属于α类岩石，出矿点α+1到出矿点β全部属于β类岩石，以此类推。

式中，约束条件(4)表示出矿点最小任务量；约束条件(5)表示出矿点最大生产能力；约束条件(6)表示受矿点最小任务量；约束条件(7)表示受矿点最大生产能力；约束条件(8)表示出矿点到受矿点的最小、最大运输量要求。

2 多目标进化算法

2.1 基于分解的多目标进化算法

通过模型构建，可以发现矿山实际配矿生产作业为多目标优化问题(Multi-objective Optimization Problems，MOPs)，该问题各目标之间通常存在冲突，无法同时得到所有目标的最优解，而是获得一组权衡各目标后的折衷解，即Pareto最优解集(Pareto Optimal Set，PS)。在求解多目标优化问题方面，多目标进化算法(Multi-objective Evolutionary Algorithms，MOEAs)凭借在一次运行下可以获得一组Pareto最优解集的优势而得到广泛研究，有效解决了传统多目标优化算法鲁棒性差、计算效率低等劣势[13]。目前MOEAs大致分为三类，不同于基于帕累托支配关系的MOEAs和基于指标的MOEAs这两类，基于分解的MOEAs在维持种群收敛性与多样性方面表现优越，从而被广泛应用于求解MOPs，其中最经典的是张青富等[14]提出的MOEA/D算法。该算法是一种通过聚合函数将多目标优化问题分解成若干个单目标优化子问题的方法，常用的分解策略为切比雪夫聚合法(Tchebycheff Approach，TCH)，TCH是一种非线性多目标聚合方法，其聚合函数定义如下：

subject tox∈Ω

(9)

2.2 MOEA/D-AU算法

2.2.1 改进动机

理想情况下，当MOEA/D算法利用公式(9)定义的每个子问题都取得最优解时，种群最终才能均匀地分布在Pareto前沿(Pareto Optimal Front，PF)。但是实际情况并非如此，由于聚合函数等高线自身的劣势，导致部分子代解在迭代过程中偏离自己的权重向量方向，从而无法较好地维持种群的多样性。

如图1所示，二维目标空间下，在6个权重向量(w1，w2，…，w6)辅助下分别获得解(A-F)，图中虚线分别为解E和解G所对应权重向量w5的聚合函数等高线。从图中可以看出，解集并没有像权重向量一样分布均匀，尤其是解B和E，虽然取得了不错的聚合函数值，但是偏离了它们相应的权重向量(w2和w5)。这是由于在更新过程中，MOEA/D算法仅仅考虑了聚合函数值，没有考虑空间位置关系。由图中聚合函数等高线可以发现，解G的聚合函数值要劣于解E，因此解G被远离权重向量w5的解E所替换，从而w5所对应的解变为解E。然而，从综合考虑种群多样性与收敛性的角度而言，解G要优于解E。此外在迭代初期，种群通常远离PF，更容易出现选择误差，这很有可能将搜索局限到PF的某一部分。

图1 二维目标空间下解分布情况示意图Fig.1 Illustration of the distribution of solutions in the 2-D objective space

针对此问题，本文设计了一种基于角度的更新策略，提出了MOEA/D-AU算法。

2.2.2 基于角度的更新策略

在上述问题的启发下，本文在更新过程中不仅仅考虑解的聚合函数值，还考虑解与所有权重向量的空间位置关系，为此提出了一种基于角度的更新策略。该策略如下：首先每一个子代解都可以根据公式(10)计算出与所有权重向量之间的夹角余弦值，式中表示F(x)与w之间的锐角，然后找出V个最大的夹角余弦值，使子代解与V个最大夹角余弦值所对应的解进行聚合函数值的比较。

(10)

如图2所示，假设V为3，子代解Y通过与所有权重向量之间的夹角余弦值进行比较，找到离它最近的3个权重向量w3、w4、w5，Y在更新过程时只需要和w3，w4，w5所对应的解C、D、E进行聚合函数值的比较即可，由图2可以发现，在空间位置的限制下，使子代解Y无法和偏离权重向量较远的解进行比较，有效避免了聚合函数本身的劣势。

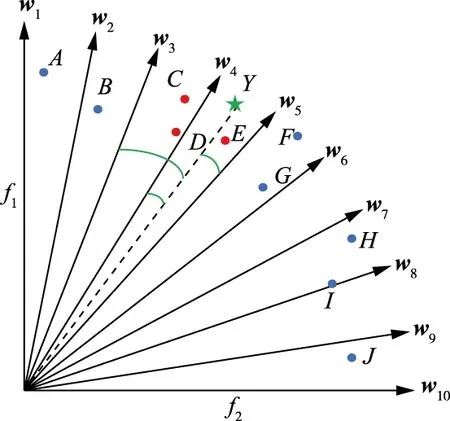
图2 二维目标空间下解与权重向量间的夹角示意图Fig.2 Illustration of the acute angle from the solution to the weight vector in the 2D objective space

采用基于角度的更新策略，相比于MOEA/D算法的更新过程，种群的更新不仅仅基于解之间的聚合函数值，还考虑了空间位置关系，从而使MOEA/D-AU算法在平衡种群多样性与收敛性方面取得很大改善。

2.2.3 MOEA/D-AU算法流程

为了便于理解，下面给出了本文算法的流程图(图3)。

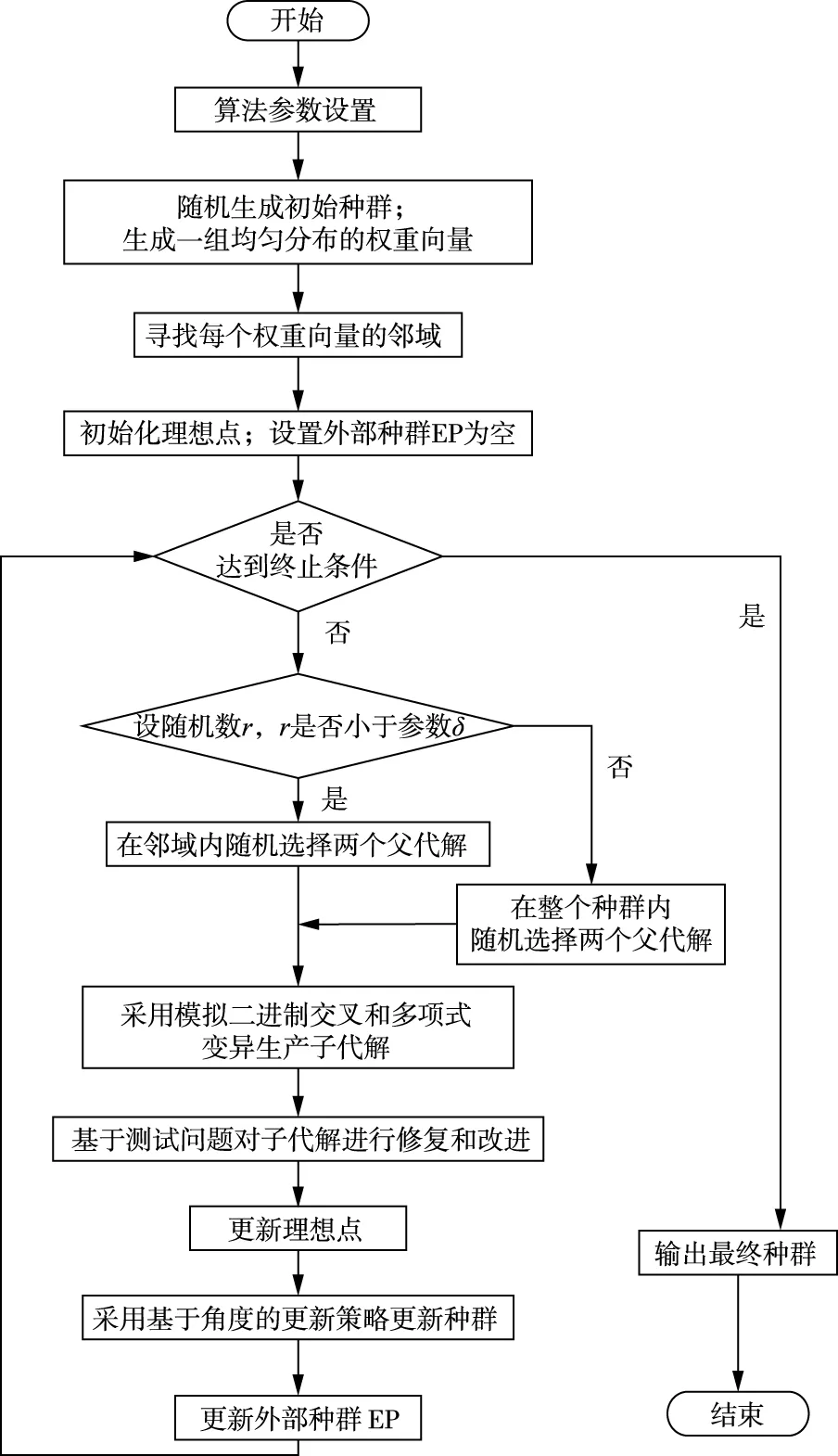
图3 MOEA/D-AU算法流程图Fig.3 Flow chart of MOEA/D-AU algorithm

2.2.4 MOEA/D-AU与MOEA/D的对比分析

为了测试本文算法MOEA/D-AU的性能，将其与原始算法MOEA/D在标准测试问题上进行仿真实验。WFG系列问题是MOEA研究领域广泛使用的代表性测试问题，本实验在WFG系列问题中随机选取WFG4、WFG6及WFG8为测试问题。此外，本实验选取国内外通用的多样性和收敛性评价标准即纯分布性PD(Pure Diversity)和世代距离GD(Generational Distance)来衡量算法求解性能[15]，其中就PD指标而言，数值越大表示算法性能越优异，相反对于GD指标，数值越小表示算法性能越优异。

为了更加形象直观地表示MOEA/D-AU相比于MOEA/D的优势，图4可视化了PD指标和GD指标下3个目标WFG4、WFG6、WFG8问题的盒图。其中，盒图的上下两条线为样本的上下四分位数，中间的线为中位数，上下虚线的顶端为最大值和最小值，“+”为异常值。由图4可以发现，在PD指标盒图方面，MOEA/D-AU不仅在3个目标WFG4、WFG6、WFG8问题上取得了最优的PD值，多样性方面优于MOEA/D，而且发现该算法的盒子长度是最短的，即算法所对应的PD指标四分位距离是最小的，即该算法的PD指标的最小值和最大值相差不大，表明MOEA/D-AU算法求出的解集整体质量更高，有更好的稳定性；在GD指标盒图方面，MOEA/D-AU在3个目标WFG4、WFG6、WFG8问题上均取得了最优的GD值，收敛性方面明显优于MOEA/D。

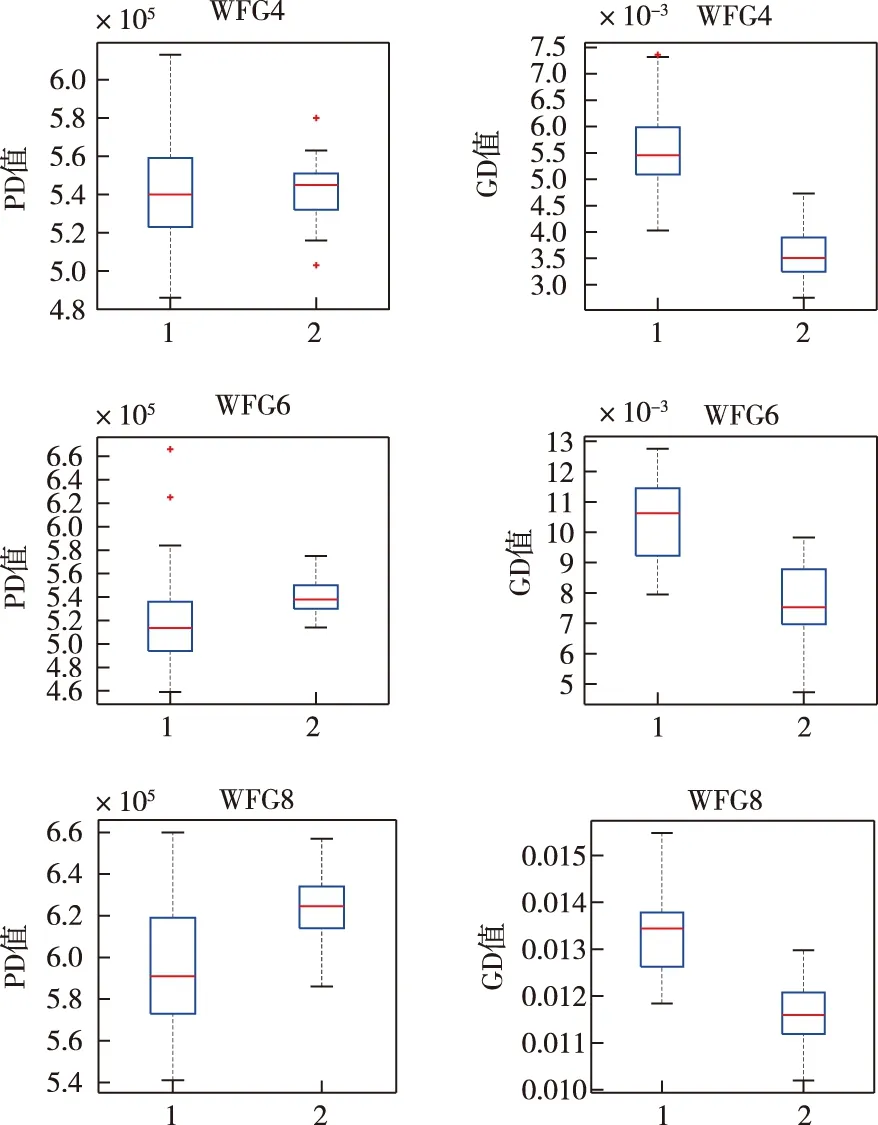
图4 3个目标WFG4、WFG6、WFG8测试问题上的PD及GD指标盒图(1：MOEA/D，2：MOEA/D-AU)Fig.4 The box plots of PD and GD indicators for the three targets WFG4，WFG6 and WFG8(1：MOEA/D，2：MOEA/D-AU)

3 综合选矿回收率预测模型

3.1 随机森林算法

随机森林(Random Forest，RF)是在应用统计学采样原理的基础上将若干个决策树集成在一起的一种算法，算法通过引入决策树的子模型数和单颗决策树的最大特征数两项重要参数有效提高了模型的抗噪能力，较好地克服了过拟合问题。此外随机森林算法既可以应用在分类问题中，也可以应用于数据的回归分析，同时凭借准确率高、参数调整简单等优势，使其相比较于SVM、BP神经网络等机器学习的方法，在默认参数下就具有较好的回归预测效果[16]。

随机森林算法步骤如下：

1)在包含M个样本的原始训练集中有放回的随机抽取M个样本，进行n次得到所有的采样数据集。

2)对所有采样数据集分别构建完全生长的决策树进行训练。

3)最终结果根据多个决策树以投票(分类问题)或求平均值(回归问题)的方式来计算测试样本的预测值。

3.2 随机森林预测模型构建

通过阅读有关选矿回收率的大量文献可以发现，嵌布粒度、氧化率和有害物质等指标和选矿回收率之间存在密切关系，因此将上述指标作为训练模型的输入参数，通过构建的随机森林模型进行训练来得到选矿回收率的预测值，模型结构如图5所示。

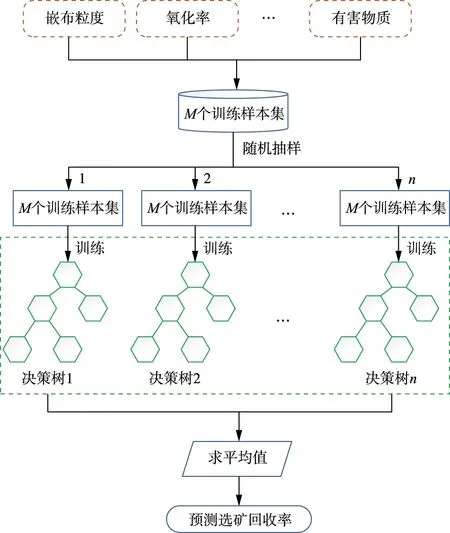
图5 选矿回收率预测模型Fig.5 Prediction model of mineral processing recovery

4 工程应用

以国内某大型金属露天矿为例进行分析研究。矿区面积2.01 km2，包含13个出矿点和3个受矿点，其中矿体中金属主要有钼、钨、铜三种，有害物质主要为二氧化硫，岩性主要有矽卡岩、透辉石长和长英角岩3种。编制合理的配矿计划，以每个出矿点到受矿点的出矿量为自变量进行算法优化，在满足各个约束条件的同时使总目标偏差最小。

矿山每班(每天3班)有10～13台电铲工作，有3个破碎站进行破碎。矿山配矿的相关参数如表2～5所示。

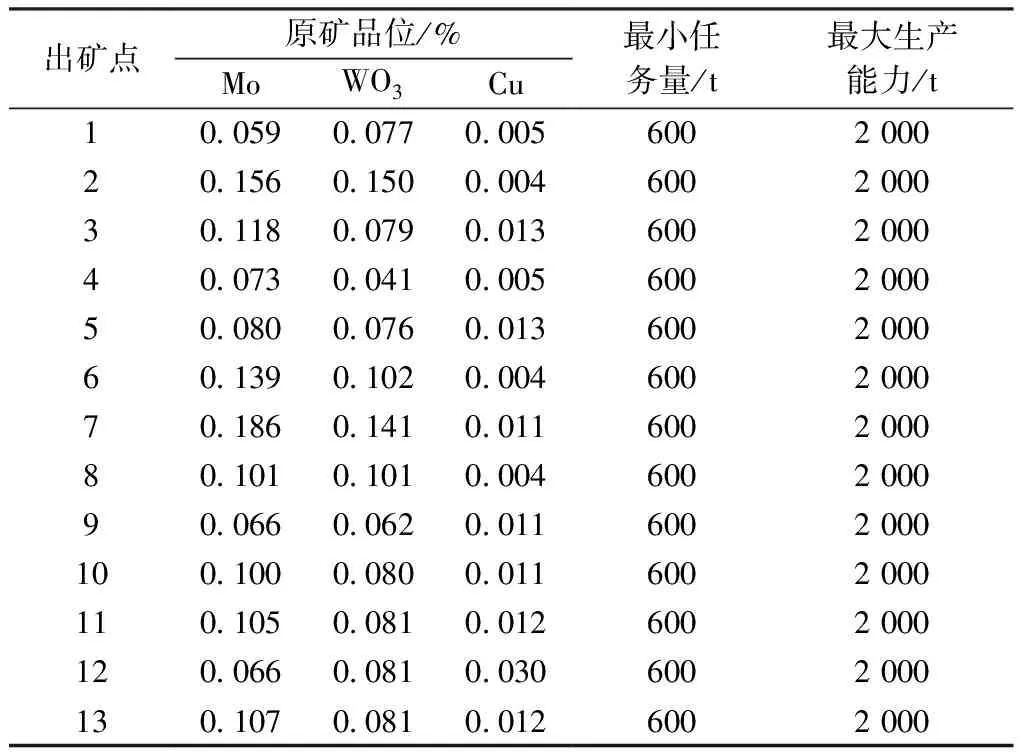
表2 配矿相关参数

表3 配矿相关参数

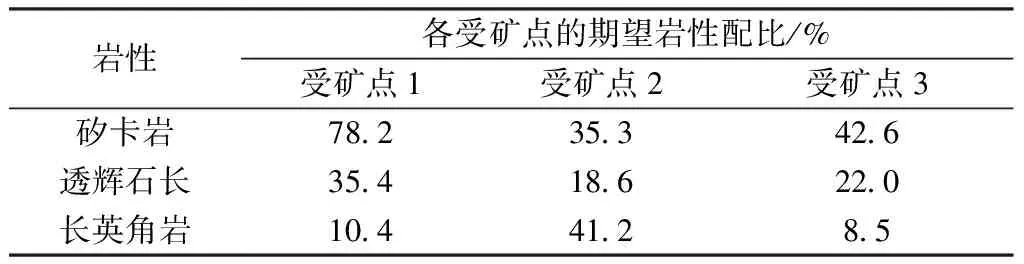
表4 配矿相关参数

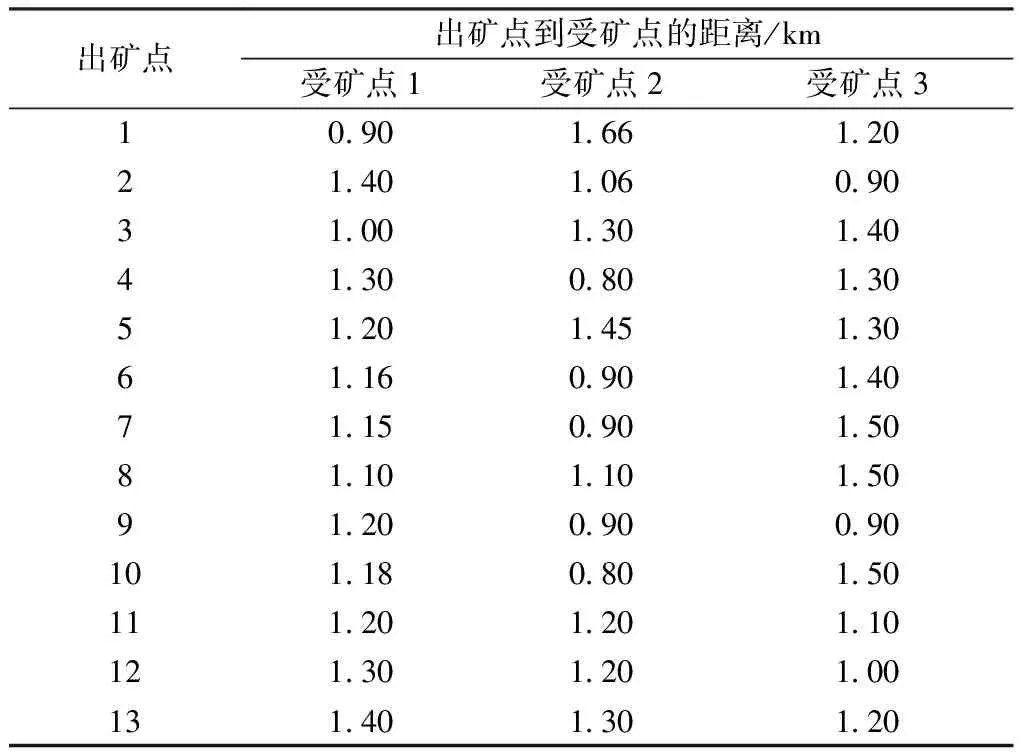
表5 配矿相关参数

将上述表中数据输入配矿模型中，利用MOEA/D-AU算法对其进行求解，得到30组配矿结果。为了提高矿石的综合回收率，构建综合选矿回收率预测模型，对30组配矿结果进行筛选，将不满足各个受矿点综合回收率指标的配矿结果舍去，从而获得最贴合实际矿山情况的配矿结果。预测模型根据此矿山实际情况和选矿厂的选矿试验，确定将矿石的氧化率和有害物质二氧化硫的浓度作为训练模型的输入参数，通过构建的随机森林模型进行训练来得到综合选矿回收率。最终从筛选后的配矿结果中随机选取一个配矿计划，如表6所示。

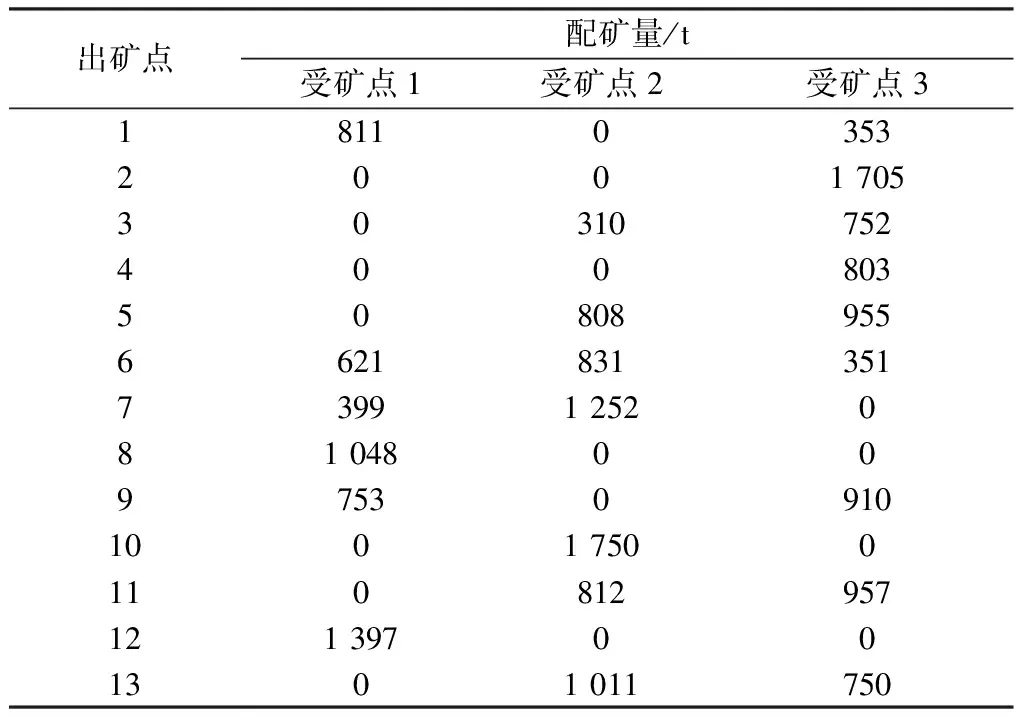
表6 配矿计划

通过计算表6中配矿计划可以发现，品位偏差和岩性配比偏差都趋近于0，生产成本也优于矿山现状，由此可知，本文所求配矿计划能够迅速找到贴合矿山实际情况的配矿结果。

为了更加直观全面地分析所得配矿计划的优势，从综合选矿回收率预测模型筛选过后的多组配矿结果中随机选择10个配矿计划，分析10个配矿计划中各个受矿点所得品位情况。图6反映了各个受矿点钼、钨、铜金属的品位情况，因选矿厂接受配矿后的矿石品位处于期望品位上下0.05%范围内，所以图中描绘了各受矿点品位上下限、各个受矿点期望的矿石品位以及求解结果。

从图6中可以看出，钼矿石在1号、2号及3号受矿点的计算品位和目标品位都相差不大；对于钨矿石，在1号、2号受矿点的计算品位多数略高于期望的目标品位，3号受矿点的计算品位有些波动，但都处于允许的品位波动范围；对于铜矿石，在1号、2号及3号受矿点品位波动都相对稳定，在期望的目标品位上下，取得理想的结果。

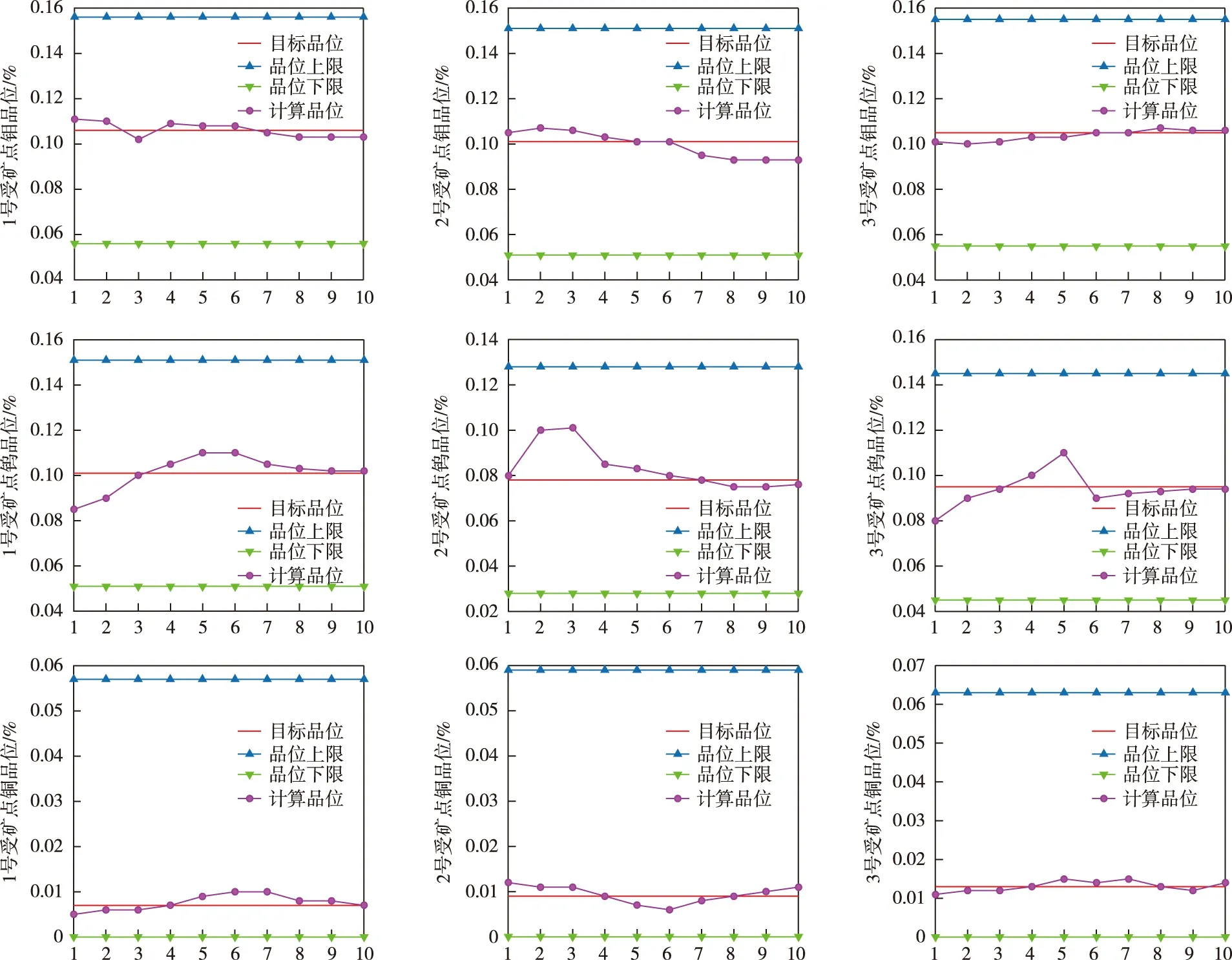
图6 钼、钨、铜三种金属计算品位情况Fig.6 Calculated grades of molybdenum，tungsten and copper

5 结论

1)本文针对露天矿多金属多目标配矿问题，以生产成本、品位偏差和矿石岩性配比偏差最小为目标函数构建了多金属多目标配矿优化模型，有效解决了多金属多目标配矿中广泛存在的配矿结果粗略等问题。

2)鉴于露天矿多金属多目标配矿模型的复杂性和约束性，在MOEA/D的基础上提出了MOEA/D-AU算法求解配矿计划，并在标准测试集上与原算法MOEA/D进行了对比验证，结果表明MOEA/D-AU算法在求解复杂多目标优化问题上具有一定优势。

3)鉴于对选矿环节的各种影响因素考虑不充分，本文根据矿山实际数据构建了融合氧化率及有害物质参数的综合回收率随机森林预测模型，通过预测模型对多目标进化算法求解的多组配矿结果进行筛选，从而得到一个更加符合矿山实际生产情况的配矿计划。