中低渗高阶煤煤岩毛管压力数学表征

陈 科，陈毅雯，刘志伟，何 伟，杨发荣，唐 磊

(中海油能源发展工程技术分公司中海油实验中心，天津 300452)

0 引言

毛管压力曲线对煤层气保存及开发具有重要影响(张芬娜等，2015；李传亮等，2017；宋金星等，2017；杨艳磊等，2017；贾慧敏等，2020)，毛管压力曲线定量表征是其推广应用的重要前提(郑小鹏等，2019；贾慧敏等，2019；王镜惠等，2020)。压汞法是研究煤岩孔隙结构的常用方法，刘顺喜和吴财芳(2016)基于压汞试验，对黔西比德-三塘盆地煤样孔隙结构进行了研究；杨师宇等(2020)利用高压压汞实验研究了乌鲁木齐河东矿区煤储层渗流孔孔隙特性；吴双等(2016)利用高压压汞法对中高煤级煤岩孔隙进行了研究。而许多学者认为压汞实验对煤岩孔隙表征不适应，提出校正方法(韩贝贝等，2015；程丽媛和李伟，2016；刘一楠等，2020)。目前煤岩毛管压力测试多采用人工粉碎后的煤岩颗粒(顾熠凡等，2016；王兆丰等，2019；李建楼和张治，2020)，测试得到的毛管压力反映的是煤岩基质孔隙对毛管压力的影响，不能反映割理裂隙对煤岩毛管压力的影响，综合反映煤岩毛管压力应该采用柱状煤样进行实验测试(Liu et al.，2016；贾慧敏等，2016)。前人对毛管压力曲线数学模型进行了较多的研究，Thomeer(1960)提出了毛管压力与进汞汞饱和度的经验关系式；而Brooks and Corey(1964)提出了著名的BC毛管压力模型，表征了毛管压力大小与湿相饱和度的关系；Li(2010a)等通过理论推理得到BC毛管压力数学模型，为BC模型提供了理论依据；贺承祖和华明琪(1998)等基于分形理论计算得到了湿相饱和度与毛管压力的定量表达关系，得到了分形毛管压力数学模型，对常规砂岩储层适应性很强；江丙友等(2010)和尹志军等(2011)应用分形毛管压力模型对煤岩进行了研究，认为必须具有不同的分形维数时才能拟合不同孔隙半径的毛管压力实验数据；曾建强等(2019)对上述方法对高阶煤储层毛管压力数学模型的适用性进行了评价，认为BC模型不适宜高煤阶煤岩毛管压力表征，Thomeer模型和贺承祖模型分别适用于中、高渗储层；Li et al.(2010b)基于分形理论提出了适用于裂缝储层的毛管压力模型，并提出了裂缝储层和非裂缝储层一般化的数学表达式；袁哲等在Li基础上，引入了迂曲度参数，进一步完善了裂缝储层的毛管压力表征公式，但整体上公式及计算方法较为复杂(袁哲和刘鹏程，2015；袁哲等，2015)。因此，适用于中、低渗储层，割理、裂隙发育的高煤阶煤岩的毛管压力曲线定量表征方法还需要进一步研究。本文基于中、低渗高阶煤岩压汞实验数据提出了一个新的毛管压力经验表达式，对实验数据适应性较好。

1 高压压汞实验及结果

1.1 煤样来源与制作

煤样选自沁水盆地高阶煤煤矿，在不规则的块状煤样上钻取直径为2.5 cm的柱状煤样，长度在5 cm左右，从中选取不同孔、渗特征的9块煤样进行高压压汞测试。

1.2 实验步骤

在室温下(21℃)采用气体孔隙度和渗透率测试仪测试煤样孔隙度和渗透率，结果如1所示。表然后在室温下(21℃)开展高压压汞实验，压汞实验严格按照石油与天然气行业标准《岩石毛管压力曲线的测定》(SY/T5346-2005)规定的操作步骤进行。

1.3 实验结果

表1表明4块煤样渗透率分布在0.01～0.1mD之间，属于低渗储层；5块样品分布在0.1～1 mD之间，属于中渗储层(孙粉锦等，2014)；9块煤样孔隙度为4%～6%，属于低孔隙度储层，表明整体物性较差。9块煤样毛管压力曲线在SHg-Pc半对数坐标中凸向左上方，表明煤样物性差、孔隙分选性差。已有研究表明，煤岩物性越好，排驱压力越小，孔隙分选性越好，中间平缓段越长，毛管压力曲线在SHg-Pc半对数坐标系中越凸向右下方(曾建强等，2019)，进而表现出与中、低渗煤样毛管压力曲线完全不同的形态，而目前对于高渗煤样毛管压力曲线适用的数学模型较多，而采用Thomeer模型、Brooks and Corey模型、Li模型及分形模型均不能很好拟合本文研究的中、低渗透煤样毛管压力曲线，因此本文适用的数学模型需要进一步研究。

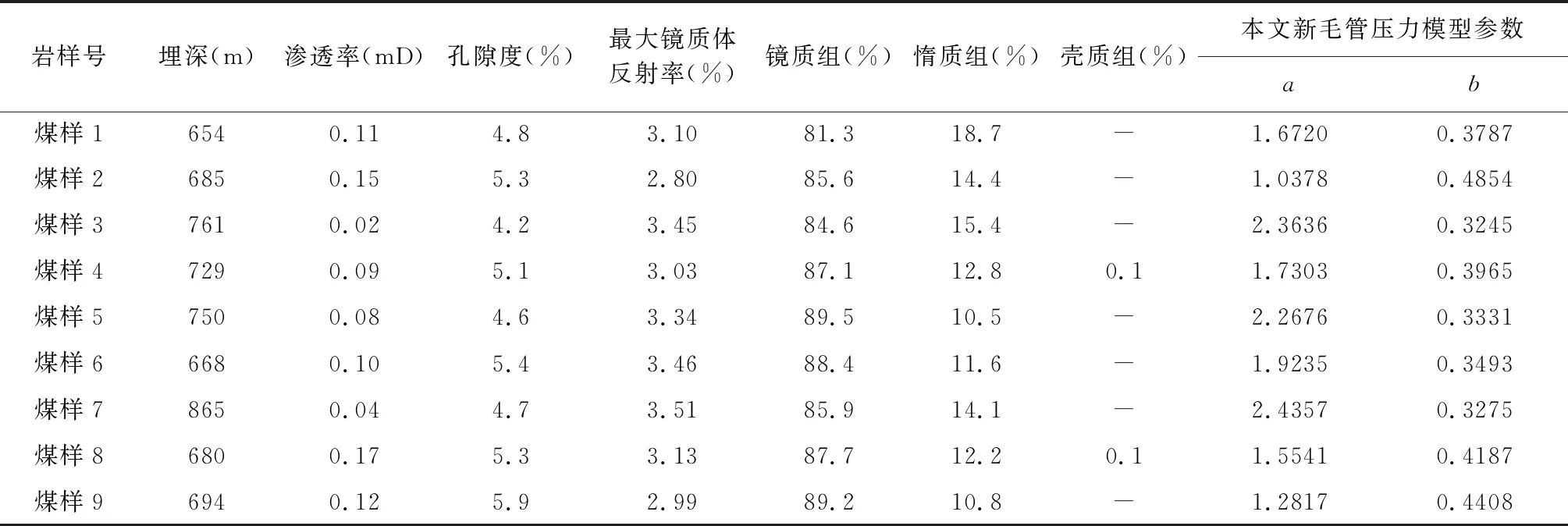
表1 实验煤样基本参数

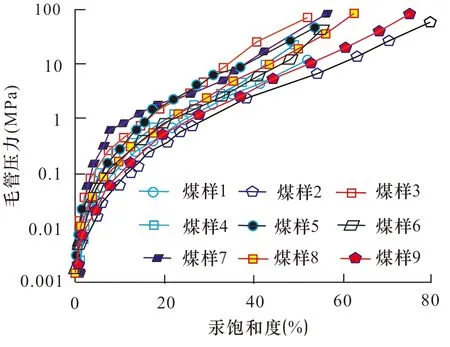
图1 9块煤样高压压汞毛管压力曲线

2 新数学模型

2.1 数学模型

图2为根据实验测试得到的煤样高压压汞数据处理得到的lnPc-lnPmin-lnSHg和SHg关系图，通过拟合回归得到下式：

lnPc-lnPmin-ln(SHg^0.5)=aSHgb

(1)

式中，Pc为毛管压力，MPa；Pmin为阀压，即汞开始进入煤样最大孔隙的压力，MPa；SHg为汞饱和度，%；a和b为常数。由图2可知，式(1)对煤样处理后的高压压汞数据拟合程度很高，均达到98%以上。

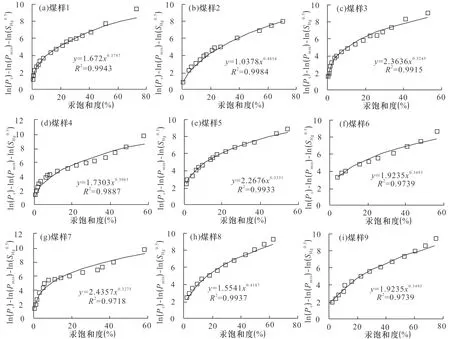
图2 实验煤样lnPc-lnPmin-lnSHg和SHg关系图

式(1)整理得：

(2)

根据式(2)，新的毛管压力计算公式为：

(3)

该模型理论上适用于所有中、低渗透煤样毛管压力曲线，但由于本研究没有获得中、低煤阶中、低渗透煤样，因此无法就该模型对中、低煤阶中、低渗透煤样毛管压力的适应性进行评价，因此更为严谨地将该模型的适用范围定义为中、低渗透高阶煤样。

2.2 参数a和b计算方法

根据公式(1)可知，在以lnPc-lnPmin-lnSHg为纵坐标，以SHg为横坐标的直角坐标系中，lnPc-lnPmin-lnSHg和SHg成幂指数关系，通过最小二乘法拟合得到a和b，结果如表1所示。将参数a、b代入式(3)得到煤样1～9的毛管压力计算公式依次为：

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

3 分析与探讨

3.1 参数a和b对毛管压力影响

基于煤样1的毛管压力曲线模型(式(4))，在其他参数不变条件下，分别模拟a为0.5、1、1.672和2时毛管压力曲线和b为0.1、0.3787、0.25和0.45时毛管压力曲线如图3所示，结果表明毛管压力随参数a和b增加而增加。

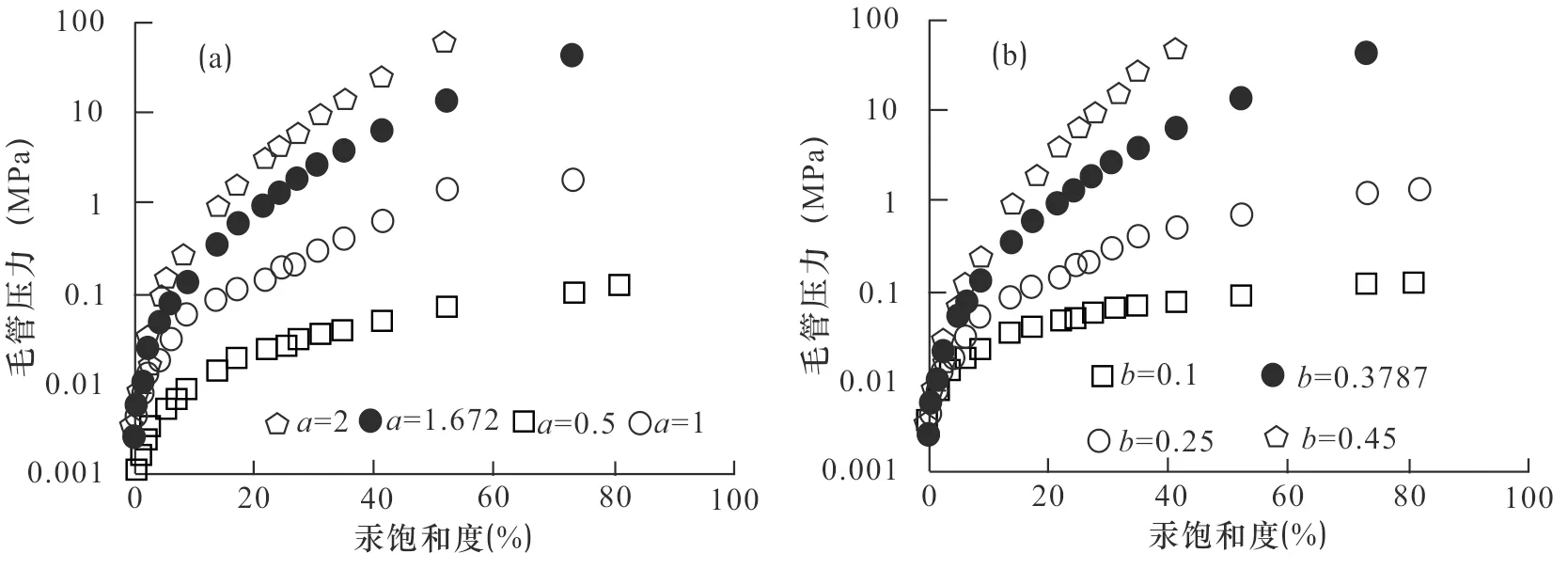
图3 参数a、b对毛管压力影响

3.2 参数a和b关系

9块煤样新型毛管压力曲线模型中参数a和b关系如图4所示，结果表明参数a随着参数b增加而降低，二者呈负幂函数关系，相关性达到0.97以上，相关性极强，即：

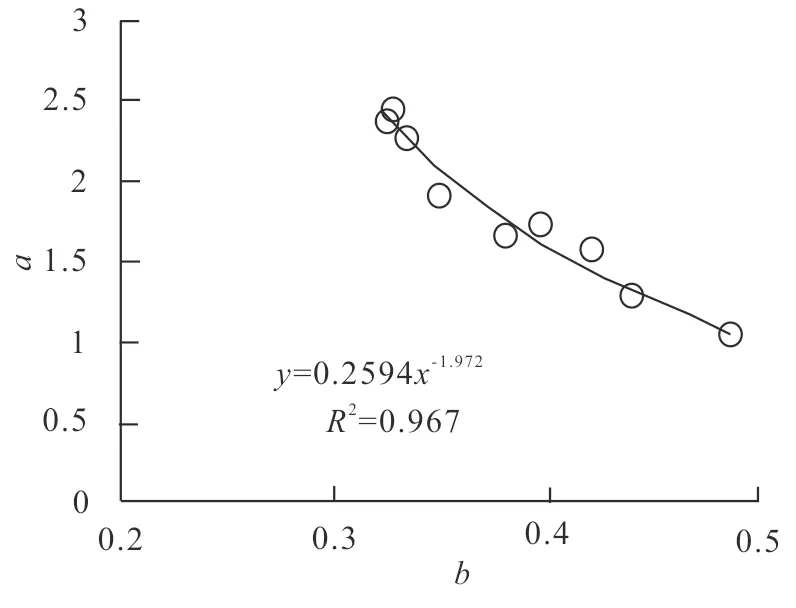
图4 参数a、b相互关系

a=0.2594b-1.972

(13)

将式(13)代入式(3)，则得到单一参数毛管压力数学模型为：

(14)

该模型进一步简化了本文提出的毛管压力模型，同时进一步简化了参数求取步骤，这是本文模型与前人模型的最大区别，不仅对实验数据拟合程度较高，还大幅降低了计算工作量。根据式(14)变化得：

(15)

根据式(15)可知，在以lnPc-lnPmin-ln(SHg^0.5)为横坐标，以SHg为纵坐标的双自然对数坐标中，lnPc-lnPmin-ln(SHg^0.5)与SHg成线性关系，直线的斜率值为b。

3.3 参数a和b与孔渗关系

图5为渗透率与参数a、b关系图。结果表明参数a值随渗透率、孔隙度增加而降低，均成线性关系，且相关性较好；参数b值随渗透率、孔隙度增加而增加，均成指数关系，且相关性较好。

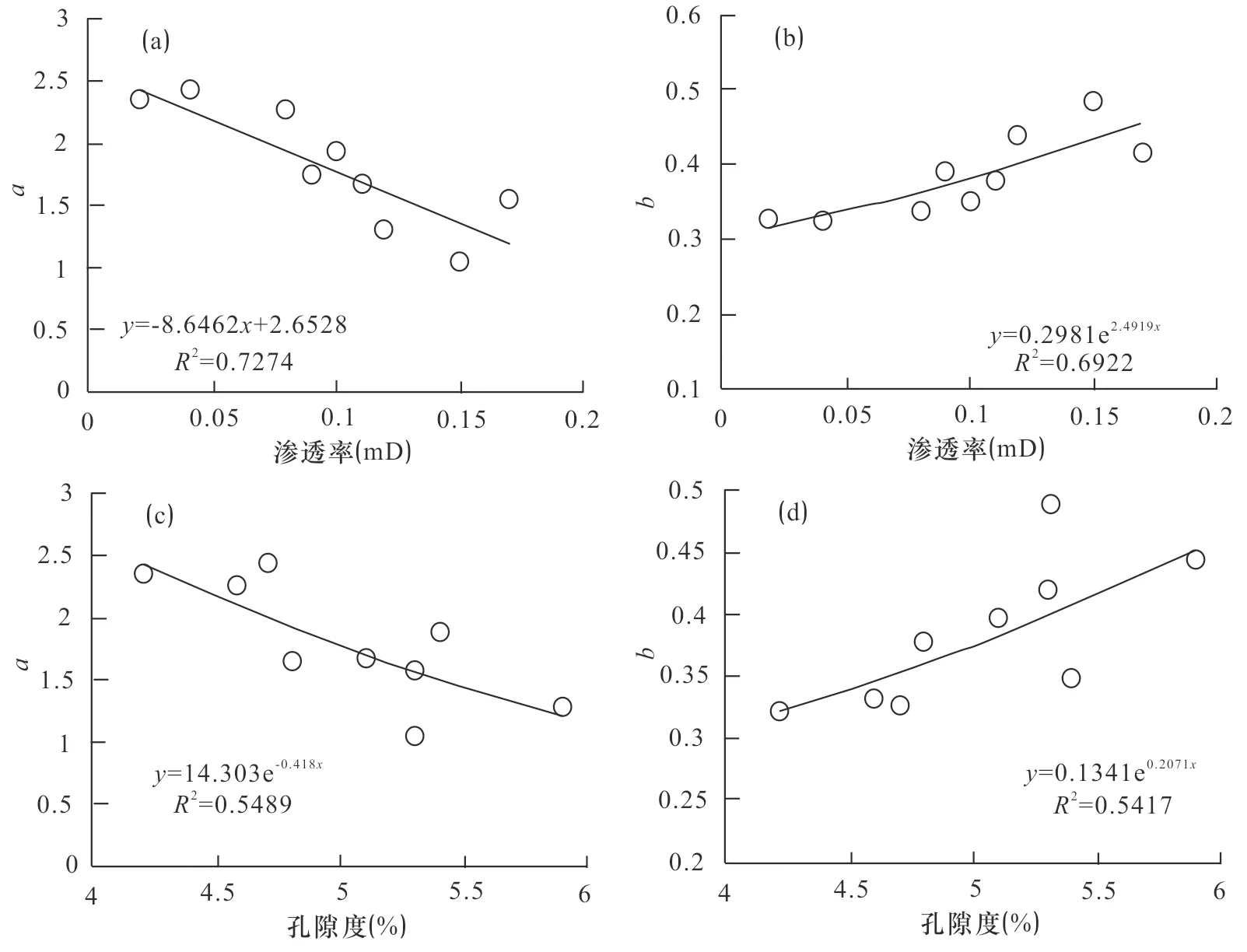
图5 不同因素对参数a、b的影响

4 结论

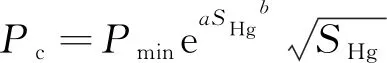
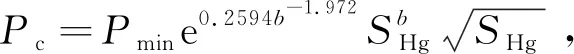
(3)毛管压力随参数a和b增加而增加；参数a值随渗透率、孔隙度增加而降低，均成线性关系；参数b值随渗透率、孔隙度增加而增加，且均成指数关系。

[附中文参考文献]

程丽媛,李伟.2016.基于压汞法的构造煤基质压缩特性及其对孔隙结构的影响[J].煤矿安全,47(2):175-179.

顾熠凡,王兆丰,戚灵灵.2016.基于压汞法的软、硬煤孔隙结构差异性研究[J].煤炭科学技术,44(4):64-67.

韩贝贝,秦勇,张政,汪岗,喻鹏.2015.基于压汞试验的煤可压缩性研究及压缩量校正[J].煤炭科学技术，43(3):68-72.

贺承祖,华明琪.1998.储层孔隙结构的分形几何描述[J].石油与天然气地质，19(1):15-23.

贾慧敏.2016.高煤阶煤岩孔隙结构分形特征研究[J].石油化工高等学校学报，29(1):53-56,85.

贾慧敏,胡秋嘉,祁空军,覃蒙扶,毛崇昊,张光波.2019.煤层气流压回升型不正常井储层伤害机理与治理[J].煤田地质与勘探,47(4):69-75.

贾慧敏,闫玲,毛崇昊,张庆,张光波,樊彬.2020.煤层气储层毛管压力对煤层气开发效果的影响[J].煤矿安全,51(5):6-9,15.

江丙友,林柏泉,吴海进,朱传杰,陆振国.2010.煤岩超微孔隙结构特征及其分形规律研究[J].湖南科技大学学报(自然科学版),25(3):15-18,28.

李传亮,朱苏阳,彭朝阳,王凤兰,杜庆龙,由春梅.2017.煤层气井突然产气机理分析[J].岩性油气藏，29(2):145-149.

李建楼,张治.2020.低温氮吸附法判识构造煤的实验研究[J].地质与勘探,56(4):838-844.

刘顺喜,吴财芳.2016.比德-三塘盆地煤储层不同尺度孔隙分形特征研究[J].煤炭科学技术,44(2):33-38,67.

刘一楠,刘勇,辛福东,魏宏宇.2020.压汞实验对低阶煤表征的适用性分析及校正方法[J].煤田地质与勘探,48(4):118-125.

宋金星,苏现波,王乾,陈培红.2017.考虑微孔超压环境的煤储层含气量计算方法[J].天然气工业,37(2):19-25.

孙粉锦,王勃,李梦溪,梁宏斌.2014.沁水盆地南部煤层气富集高产主控地质因素[J].石油学报，35(6):1070-1079.

王镜惠,尹宇寒,梅明华,刘娟,王华军.2020.高煤阶煤储层解吸曲线定量表征及解吸参数研究[J].地质与勘探,56(5):1096-1104.

王兆丰,岳基伟,俞宏庆,李学臣.2019.复合煤层物性差异性试验研究[J].煤炭科学技术,47(7):31-38.

吴双,汤达祯,许浩,李松.2016.中-高煤级煤岩孔隙发育特征[J].煤田地质与勘探，44(6):69-74.

杨师宇,姚艳斌,魏韧,张静仪.2020.乌鲁木齐河东矿区煤储层渗流孔孔隙分形特征研究[J].煤炭科学技术，48(8):175-183.

杨艳磊,吴丛丛,左银卿,杨兆彪,陈龙伟,王晶.2017.高阶煤储层微观系统水浸入程度对产能的控制[J].煤炭技术,36(11):104-106.

尹志军,盛国君,王春光.2011.基于压汞法的煤岩各段孔隙的分形特征[J].金属矿山,40(9):54-57.

袁哲,刘鹏程.2015.一个适用于煤岩的新的分形毛管力模型[J].科学技术与工程,15(9):63-67.

袁哲,刘鹏程,冯高城.2015.分形维数定量表征煤岩储层非均质性[J].中国科技论文,10(9):1010-1013.

曾建强,华彬,谭政林.2019.高煤阶煤层气储层毛管压力数学模型适应性评价[J].煤矿安全,50(9):17-20.

张芬娜,李明忠,綦耀光,陈波,孟尚志.2015.低渗透煤层气产气通道渗流门限分析[J].中国矿业大学学报,44(6):1025-1032.

郑小鹏,王蕾蕾,刘道天,田冷,门成全,赵芙蕾.2019.基于分形理论的高煤阶煤层气储层气-水相渗计算方法及应用[J].煤矿安全，50(7):10-13.