基于OpenSees的城市高架桥弹塑性抗震分析

赵 杰， 温林莉， 王桂萱

(大连大学 土木工程技术研究与开发中心， 辽宁 大连 116622)

0 引言

近年来，随着我国经济建设突飞猛进，桥梁工程的建设也飞速发展，在城市及城市群间建造了大量高架桥梁，高架桥梁是现代交通命脉和城市生命线工程的重要组成部分，确保其在地震作用下的安全性具有重要的战略意义和巨大经济效益[1-2]。

桥梁抗震是一直以来国内外学者不断研究的课题，对桥梁的抗震分析主要从桥墩和全桥两个方面入手。王红伟[3]等采用Pushover分析法对钢筋混凝土双柱墩的抗震性能进行数值验算，研究墩高和配筋率对钢筋混凝土双柱墩位移延性的影响。龙佩恒[4]等基于Midas/Civil建立混凝土连续梁桥双柱墩有限元分析模型，采用弹性反应谱法、弹塑性反应谱法、Pushover分析法、动力时程分析4种方法计算桥梁的地震响应，研究双墩柱抗震性能。胡章亮[5]基于OpenSees软件建立某6跨RC连续梁桥非线性动力时程分析有限元模型，以墩顶位移、墩底截面轴力和墩底截面弯矩为指标，研究近场地震动对钢筋混凝土连续梁桥的影响。BILLAH[6]等对加固改造后的多柱排架桥的抗震性能进行全方面的模拟，利用有限元分析工具建立了改造后桥梁排架的分析模型，并与试验结果进行了对比验证。

为了研究城市高架连续梁桥的抗震性能，本文从构件和结构2个层次对桥梁进行抗震性能分析。在构件层次，采用Pushover静力弹塑性分析和低周往复荷载作用下的非线性分析对单根桥墩进行数值模拟；结构层次是对整座桥梁的抗震性能分析，梁式桥的抗震性能主要通过地震作用下各构件的内力和位移响应量来评估。对整桥进行E2地震作用下的动力时程计算，给出桥墩的内力(弯矩、剪力)、墩顶位移、截面弯矩曲率曲线等参数，通过对各参数的分析来评价桥梁结构的抗震性能。

1 计算分析原理

1.1 OpenSees纤维模型

纤维模型是指将纤维截面赋予梁柱构件(即该构件的每一个截面都定义为纤维截面)。主要思路为将各控制截面沿单元纵向离散为若干个小的纤维，假定每根纤维处于单轴应力应变状态、应变分布均匀，且认为整个纤维截面满足平截面假定，根据相应纤维材料的单轴应力-应变关系即可计算得到整个截面的力-变形非线性关系。如图1所示，纤维截面主要离散化为保护层混凝土、核心混凝土和钢筋层3个部分，构件的材料和钢筋的分布特点可以很好地在纤维模型中体现出来，纤维模型自动考虑双向弯曲和轴力之间的耦合作用，从而有效地模拟构件弯曲变形和轴向变形。纤维模型还可考虑箍筋对核心混凝土的约束效应、混凝土非线性软化及强化行为、纵筋在反复荷载作用下的屈曲破坏及包辛格效应等等[7-8]，对于钢筋混凝土截面在弯曲破坏下的非线性行为，能够得到较准确的模拟结果。

图1 纤维截面的划分Figure 1 Division of fiber section

1.2 基于力的纤维梁柱单元

基于力的纤维梁柱单元(Force-based Beam-column Element，简写FBE)也可以称作基于柔度法的梁柱单元。FBE单元允许刚度沿着杆件长度变化，基于截面力插值函数，确定单元控制截面的各截面抗力和截面刚度，根据Gaus-Lobatto积分方法计算单元抗力和刚度，以局部坐标系下的二维结构单元为例，见图2。在不考虑单元分布荷载任意变化的前提下，对于假定好的内力分布情况，杆件处于任何状态下都能够绝对满足力的平衡条件[9]。FBE单元有很好的计算精度，一般情况下一个杆件由一个单元来模拟即可，且在杆件进入强非线性阶段后可以较真实地反映单元的受力情况。

图2 局部坐标系下的二维单元Figure 2 Two-dimensional element in local coordinate system

1.3 材料本构模型

连续梁桥上部结构和桥墩的混凝土均采用OpenSees中的Concrete 01材料模型，模型的受压骨架曲线采用的是Scott修正的Kent-Park模型[10-11]，如图3所示，骨架曲线分3段：

图3 Concrete01应力 — 应变骨架曲线Figure 3 Stress-strain curve of Concrete 01

ε≤εcc时，

(1)

εcc≤ε≤εcu时，

(2)

ε>εcu时，

f=0.2Kfco

(3)

其中，fcc、fco分别为核心和保护层混凝土抗压强度；εcc、εc0分别为核心和保护层混凝土应力峰值对应的应变；εcu为混凝土的极限压应变；K为应力应变增大系数；Z为应变下降段的斜率。Concrete 01材料模型较为简单，数值模型好，能够反映混凝土因箍筋约束而产生的强度提高和峰值应变增大的特点，不考虑混凝土的抗拉强度。

模型中纵筋和耗能钢筋选用OpenSees中的Steel 02本构模型模拟，其应力-应变关系是在Giuffre-Menegotto-Pinto模型[12]的基础上发展而来的，图4为Steel 02本构模型骨架曲线。图4中：fy为钢筋屈服应力；Es为钢筋弹性模量；Ep为屈服后模量。见图5，该本构模型能够较好地反映钢筋的Bauschinger效应和循环应变强化等。

图4 Steel 02应力-应变关系Figure 4 Stress-strain relationship of steel 02

图5 钢筋循环特性Figure 5 Cyclic properties of reinforcement

1.4 单元地震破坏准则

OpenSees软件为用户提供的收敛准则有3种，分别为： ①位移准则(Norm Displacement Increment Test)，其收敛公式如式(4)；②力准则(Norm Unbalance Test)，其收敛公式如式(5)；③能量准则(Energy Increment Test)，其收敛公式如式(6)。

(4)

(5)

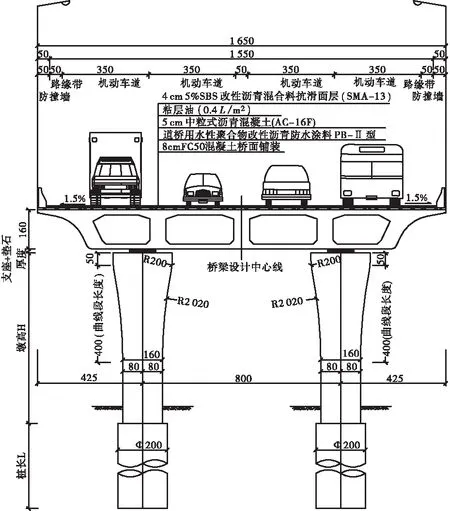
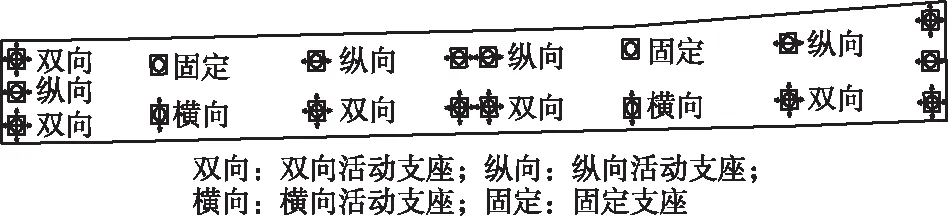
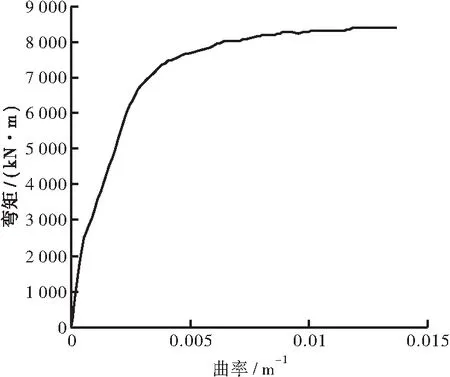
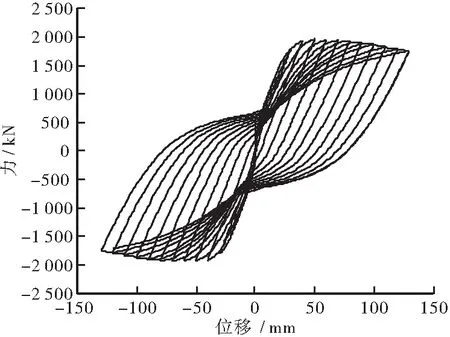
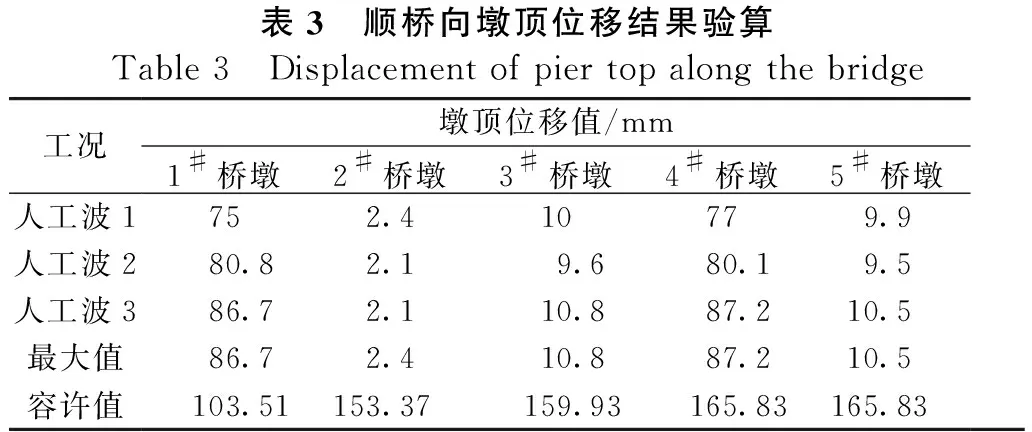
1/2(ΔUTR)

(6)

式中:R表示力增量；ΔU表示位移增量；tol表示规定公差。

随着变形逐渐增大，钢筋混凝土构件的刚度变得越来越小，较小的荷载增加可能导致结构的产生较大变形，引发力的跳跃。能量准则在迭代过程中可以同时控制力和位移的增量，稳定性较好，因此本文选取能量准则作为判定准则[13]。

2 数值模拟实例

2.1 工程概况

如图6所示，该段桥梁为一座六跨钢筋混凝土连续梁桥，上部结构为6×30 m的钢筋混凝土主梁，主梁为现浇连续箱梁，采用C50混凝土，钢筋采用HRB400，梁高1.6 m，采用单箱多室截面形式。下部结构为钢筋混凝土双柱墩，采用C40混凝土，1～3号墩中心距为8 m，4号墩为躲避桥下辅助墩，桥墩中心距调整为11.95 m，5号墩中心距为9.1 m。双墩采用φ1.6 m圆形截面，中墩上部横向扩大为1.6×2.4圆端形墩帽，交接墩纵向扩大为1.6×2.4圆端形墩帽，下设φ2.0 m钻孔灌注桩，桥墩标准纵断面图见图7。支座有固定支座、横向滑动支座、纵向滑动支座、双向滑动支座4种布置形式，其具体布置形式如图8所示。

图6 桥梁立面图Figure 6 Elevation of bridge

图7 标准纵断面图Figure 7 Standard profile view

图8 支座布置图Figure 8 Layout of bearing

2.2 有限元模型

利用OpenSees建立高架桥的数值仿真模型，单元数为170，节点数为211，动力模型如图9所示。从理论上讲，大多数桥梁主梁在地震作用下保持弹性，因此采用OpenSees中的弹性梁柱单元(Elastic Beam Column Element)来模拟钢筋混凝土箱形梁，每3 m划分一个单元；采用FBE单元来模拟混凝土双柱墩，每个桥墩划分为5个单元，每个单元设3个积分点；对于支座采用零长度转动弹簧单元，对每个方向分别赋予不同的刚度，固定支座直接约束与主梁之间的平动，横桥向转动以及扭转自由度，本文不考虑桩土之间的相互作用，桥墩底部采用固定约束。采用Zero Length Element和Equal DOF组合命令处理OpenSees中的多点约束，以实现构件的逐步失效。计算分析得该连续梁桥一阶自振频率为1.228 521，基本周期为0.813 987 s，观察前10阶模态可知主要以(反)对称侧弯和(反)对称竖弯为主，表1记录了前10阶的自振周期与频率以及振型反应特征。

图9 全桥模型Figure 9 Full bridge model

表1 高架桥的动力特性Table 1 Dynamic characteristics of viaduct振型阶数频率/Hz周期/s振型特征11.228 5210.813 987固定桥墩顺桥向弯曲(两幅同向)21.241 1020.805 736一阶反对称侧弯,内侧桥墩顺桥向弯曲33.139 2290.318 55一阶对称反弯,桥墩顺桥向弯曲(两幅反向)43.238 2110.308 813主梁对称竖弯53.433 3750.291 259主梁反对称竖弯64.078 9390.245 162中间跨桥墩顺桥向弯曲(两幅同向)74.838 5150.206 675主梁对称竖弯85.693 1510.175 65中间跨桥墩顺桥向弯曲(两幅同向)95.839 2440.171 255主梁对称侧弯106.411 760.155 963主梁对称竖弯

2.3 地震动输入

本桥未进行地震安全评价，因此采用《城市桥梁抗震设计规范》(CJJ 166-2011)第5.2条规定采用设计加速度反应谱，根据本桥地质报告，地震烈度为7°，设计地震分组为第2组，场地类别为Ⅱ类，E2水准为50 a超越概率2%，根据规范中计算公式计算得出水平设计加速反应谱，如图10。

图10 E2地震作用加速度反应谱Figure 10 Acceleration response spectrum of earthquake action

计算得到E2地震作用加速度反应谱后，以此反应谱为目标谱输入SIMQKE软件生成人工地震波，考虑到地震动的随机性，取3条相关系数小于0.1的人工地震动对结构进行非线性分析。图11为人工地震反应谱曲线，可以看出人工地震波反应谱曲线与根据规范计算所得反应谱曲线拟合较好，人工地震动峰值加速度为0.22g，持续时长为30 s，加速度时程曲线见图12。

图11 计算谱与目标谱拟合结果Figure 11 Calculation spectrum and target spectrum fitting results

3 抗震性能分析结果

3.1 桥墩静力弹塑性分析

对于本文分析的连续梁高架桥，在E2地震作用下，地震力主要集中于固定墩处，塑性展开也主要集中于本桥的4根固定桥墩，以1#固定墩为研究对象对其进行静力弹塑性分析(Pushover+低周往复)，得到桥墩的一些抗震性能参数，如开裂点、承载能力、变形能力、屈服点、极限点等等。

3.1.1桥墩Pushover静力弹塑性分析

首先，建立单墩的纤维模型，将其划分为6个单元，每个单元设置3个积分点，墩底采用全约束，由于只对结构进行平面受力分析，因此对墩顶节点的自由度进行平面外的约束(平面外Y方向的平动，且约束对应的转动分量)，以提高收敛性；其次对墩顶施加4 821 kN的轴压力，采用位移控制的方法逐渐增加柱顶位移值直至结构破坏，位移控制点为墩顶节点，位移自由度为1，水平位移推动每一步为1 mm，共进行200步计算。桥墩在计算过程中经历了开裂、屈服、极限破坏共3个阶段，柱顶变形与内力结果如图13所示，柱底截面弯矩-曲率曲线如图14所示。为了确保计算的准确性，采用XTACT软件对截面进行二次分析，将二者的结果进行对比分析，得到的截面弯矩-曲率曲线如图15所示。

图13 力-位移曲线Figure 13 Force-displacement curve

图14 柱底截面弯矩-曲率曲线Figure 14 Moment-curvature curve

图15 XTRACT计算结果Figure 15 Calculation results of Xtract

将实际的弯矩-曲率曲线和力-位移曲线等效为相应的理想弹塑性曲线，得到桥墩的一些性能参数如表2所示，表2同时给出了桥墩位移延性系数和截面曲率延性系数，符合规范要求。构件的破坏模式直接由承载力决定，在此将构件破坏模式假设为弯曲破坏，则控制荷载为抗弯承载力，将极限弯矩认为是抗弯承载力，综合计算结果桥墩抗弯承载力为8 895 kN·m，对应的剪力数值为1 660.12 kN。

表2 变形能力及延性系数Table 2 Deformation capacity and ductility coefficient顺桥向屈服位移Δy/mm极限位移Δu/mm位移延性系数Δu /ΔyPushover21.39105.674.94XTRACT———平均值21.39105.674.94屈服曲率φy/m-1极限曲率φu/m-1曲率延性系数φu/φy等效屈服弯矩/(kN·m)0.002 920.014 95.1037 0950.002 470.013 75.5476 7410.002 860.014 95.3256 918

3.1.2桥墩滞回性能静力弹塑性分析

通过对桥墩施加低周往复荷载来计算桥墩的滞回性能。低周往复荷载即多次往复循环作用的静力，是使桥墩在正反两个方向重复加载和卸载的过程，可以很好地模拟地震作用时桥墩在承受正负交替的往复振动中的受力和变形特征。

加载制度如下：首先对桥墩施加4 821 kN的重力荷载，荷载倍数为1，分1步加载；保持上述的重力荷载不变，对墩顶部施加1 000 kN的水平荷载，采用位移控制的加载方式，控制节点为桥墩顶部节点，控制自由度为1，分析步数为100步，加载位移分别为10、20、30 mm等，直至结构破坏(计算不收敛，程序停止运行)，具体加载方案如图16所示。

图16 加载制度Figure 16 Loading system

桥墩的顺桥向滞回曲线如图17所示，骨架曲线如图18所示，固定墩滞回曲线呈弓形，曲线中间段由于构件剪切变形产生的斜裂纹张合产生捏拢现象，弓形的滞回曲线主要出现在混凝土压弯构件，符合桥墩的受力特征，曲线较饱满，在构件进入塑性阶段后表现出了良好的耗能能力。

图17 滞回曲线Figure 17 Hysteresis curve

图18 骨架曲线Figure 18 Skeleton curve

3.2 全桥动力弹塑性时程分析

对整个连续梁桥进行7°E2(0.22g)地震作用下的动力时程分析，对于顺桥向输入的情况，地震力要集中于1#、4#、6#和9#共4根固定桥墩上，控制截面为1#、4#、6#和9#墩墩底截面。地震作用下双柱墩左右两桥墩的地震响应结果基本一致，本文取一侧桥墩(1#～5#)记录地震响应结果。

3.2.1位移结果分析

记录地震动每一个时刻对应的桥墩墩顶位移值绘制成位移时程曲线，由于篇幅原因仅给出1#、4#固定墩的位移时程曲线，如图19所示。将1#～5#桥墩在3条人工波作用下的位移最大值整理于表3，位移容许值取Pushover分析和规范计算的平均值。从图表中可以看出桥墩较大的变形发生于1#和4#墩的墩顶，且位移值远大于2#、3#、5#桥墩位移值，这主要是因为顺桥向地震作用下地震力主要集中于1#、4#固定墩处，计算结果是符合实际情况的，1#墩和4#墩墩顶位移最大值分别为86.7 mm和87.2 mm，均满足规范要求，桥墩处于安全状态展现良好的性能且未发生坍塌。

(a) 1#墩

表3 顺桥向墩顶位移结果验算Table 3 Displacement of pier top along the bridge工况墩顶位移值/mm1#桥墩2#桥墩3#桥墩4#桥墩5#桥墩人工波1752.410779.9人工波280.82.19.680.19.5人工波386.72.110.887.210.5最大值86.72.410.887.210.5容许值103.51153.37159.93165.83165.83

3.2.2内力结果分析

桥墩的内力可以作为评价桥墩抗震性能的一种指标，将桥墩的剪力和弯矩值对应于地震动每一个时刻绘成时程曲线，1#、4#桥墩墩底剪力和弯矩时程曲线分别如图20和图21所示，将3条人工波中对应的剪力和弯矩最大值汇总于表4，从表中可以看出桥墩内力最大值发生在1#和4#两固定墩处，根据地震力按刚度分配的原则，计算结果符合实际情况。剪力和弯矩最大值均发生在1#墩墩底，数值分别为1 639.69 kN和7 440.77 kN·m，满足极限承载力的要求，桥墩进入塑性阶段但并未倒塌，由此看来1#墩比4#墩更易受损。

(a) 1#墩

(a) 1#墩

表4 顺桥向桥墩内力结果验算Table 4 Internal force results of the bridge to the pier内力剪力/kN弯矩/(kN·m)1#墩2#墩3#墩4#墩5#墩1#墩2#墩3#墩4#墩5#墩人工波11 624.21130.29231.99672.22300.367 364.96398.8978.96 056.16967.56工况人工波21 621.83207.84231.24714.24232.617 247.02338.19904.566 416902.84人工波31 639.69196.02245.18748.03279.697 440.77336.751 044.646 309.641 021.86最大值 1 639.69207.84245.18748.03300.367 440.77398.81 044.646 4161 021.86

3.2.3桥墩截面弯矩-曲率结果分析

截面的非线性滞回性能在结构非线性分析的过程中经常会用来描述截面的抗震性能，梁柱的截面非线性滞回性能一般情况下通过截面的弯矩-曲率曲线来描述。1#墩和4#墩在3条人工波作用下的墩底截面M-φ曲线分别如图22、图23、图24所示。从图中可以看出在7°E2地震作用下1#墩已经进入塑性阶段，滞回曲线较为饱满表现了良好的耗能能力，4#墩处于弹性阶段且即将进入塑性，表明该连续梁桥在地震作用下1#桥墩(边墩)比4#桥墩(中间墩)更为薄弱易损，这与内力结果相符合。

(a) 1#墩

(a) 1#墩

(a) 1#墩

图25给出了2#、3#、5#非固定桥墩在7°E2(0.22g)3条人工波作用下的墩底截面弯矩曲率曲线，曲线呈线性状态且弯矩和曲率远远小于屈服弯矩和屈服曲率，仍处于弹性阶段。主要是因为滑动支座的存在，2#、3#、5#非固定墩在地震作用下仅仅承受自身产生的惯性力和摩擦阻力的作用，同样7#、8#、10#非固定墩也处于弹性状态。

(a) 2#墩

4 结论

本文基于OpenSees建立高架桥三维有限元纤维模型，采用静力和动力非线性分析方法，从构件层次和结构层次对高架桥进行抗震性能分析，研究其的抗震性能，具体结果如下：

a.桥墩位移延性系数和截面曲率延性系数分别为4.94和5.325，桥墩抗弯承载力为8 895 kN·m，对应的剪力数值为1 660.12 kN，符合规范要求。

b.低周往复荷载作用下桥墩滞回曲线呈弓形，曲线中间段捏拢，符合桥墩的受力特征，曲线形状较饱满，在构件进入塑性阶段后表现出了良好的耗能能力。

c.地震作用下结构变形最大值发生在2#固定墩处分别为86.7 mm和87.2 mm；剪力和弯矩最大值发生在1#固定墩墩底，分别为1 639.69 kN、7 440.77 kN·m，满足极限承载的要求。

d.全桥在7°E2(0.22g)顺桥向地震作用下处于安全状态，塑形展开主要集中在1#固定墩(边墩)和4#固定墩(中间墩)墩底，这些部位为该桥梁的薄弱易损部位，需进行配筋加强，且相较于中间固定墩，边墩固定墩更易受损。