基于改进欧式聚类的激光雷达目标检测

王凯歌 冯 辉 徐海祥 胡 勇

(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学船海与能源动力工程学院2) 武汉 430063)(上海交大海洋水下工程科学研究院有限公司3) 上海 200231)

0 引 言

激光雷达由于测量精度高、响应速度快、抗干扰能力强、可以很好的表征外部环境等优点而被广泛地应用于无人系统领域，其在无人机、无人车、无人船上的使用已经得到了较好的发展.激光雷达目标检测的核心是点云的聚类，点云聚类的算法一般分为传统的聚类算法和基于模型的机器学习聚类算法两类.传统的点云聚类方法主要包括基于密度的DBSCAN聚类算法[1-3]、基于划分的K-Means聚类算法[4-5]、区域增长法[6]、基于空间距离远近的欧式聚类算法等.其中，DBSCAN聚类算法可以发现任意形状的点云簇，对噪声点不敏感，但数据量大时聚类所需的时间较长.文献[3]针对密度不均的点云数据，通过建立参数列表使得参数随着距离的增加而合理地增大，改善了密度聚类的效果.K-means聚类算法原理简单、聚类速度快，但需要人为的指定聚类簇数，对噪声点较为敏感且只能发现球状簇.区域增长法可以依据不同的属性，例如，曲率、法向量、几何特性等对点云进行聚类，但当数据包含噪声或点云属性分布不均时会大幅影响分割效果.李仁忠等[7-8]通过估算点云数据的曲率大小, 将曲率最小点设置为种子节点，从点云数据最平坦的区域开始生长，解决了传统区域生长法分割不稳定的问题.欧式聚类算法在距离阈值设定合理的前提下有较好的聚类效果，聚类速度较快，适用于实时的点云目标检测，但对距离阈值的选取较为敏感，聚类时需要选取正确的距离阈值，过大或过小的距离阈值都会影响聚类效果.吴燕雄等[9]在传统欧式聚类算法中加入了平滑阈值的约束来防止欠分割和过分割的现象.田青华等[10]以模板物体的点云分布情况作为聚类标准，提出了一种距离阈值自适应的欧式聚类算法并应用于工件的点云聚类.刘畅等[11]按测量距离将点云划分到不同的区域，在不同的区域内设定了不同的距离阈值，并在路面目标的检测上进行了算法验证.

文中以无人车的三维点云数据为例，针对传统欧式聚类距离阈值较难选取，选取不当时会产生聚类目标过分割或欠分割，造成目标分割不准确的问题，对传统的欧式聚类进行了改进.选取了范围较大的距离阈值区间，区间内的距离阈值较大以避免产生过分割现象；在传统的欧式聚类搜索过程中，对聚类目标和干扰目标的激光点设定不同的激光点权值，然后去除搜索过程中干扰目标的激光点，较好地解决了大距离阈值时产生的欠分割现象；对比了传统的欧式聚类和改进之后的欧式聚类在聚类效果和速度方面的差异.尽管该方法采用的数据是无人车三维点云数据，但是该方法可以扩展到机器人、无人船等领域.实验结果表明，改进之后的欧式聚类算法在选取的距离阈值区间内都有较好的聚类效果，降低了距离阈值选取的难度.

1 地面点云与非面地点云分割

由于地面点云对非地面点云聚类的影响较大，会干扰非地面点云聚类的效果，因此在进行聚类之前将地面点云去除.同一区域的地面点云其曲率一般不会有不规则的突兀的变化，因此将地面近似为平面选用RANSAC平面拟合算法来去除地面点云.

RANSAC平面拟合算法的核心是随机抽样性和假设性.其算法思路如下:①在一帧裁剪后的点云图像的点云集合G={Pi=(x,y,z)|i=1,2,3,…,n}中随机的选取三个点，利用这三个点的空间坐标确定三个点所在的平面，并设定一个距离阈值Dthres；②计算点云集合G中剩余的点到上述确定平面的距离di，将集合G中到上述确定平面的距离小于距离阈值(diDthres)的点作为非地面点.③重复上述的过程若干次选取数量最多的一组地面点云作为最终的地面点云将其去除，将对应的非地面点云保留用于聚类.

为防止地面目标较多时拟合出非地面点云部分的平面，同时减少地面点和非地面点分割所用的时间，在进行RANSAC平面拟合算法之前先提取一定高度以下的点云，将提取后的点云进行RANSAC平面拟合算法分离出地面部分的点云，见图1.

图1 地面点与非地面点分割

2 传统欧式聚类方法

欧式聚类是一种区域增长式的聚类方式，基于点与点的空间距离，将空间距离比较近的点归为一类.其原理如下：①依据待分割的点云数据建立对应的KD-tree，KD-tree是一种高纬索引的树形数据结构，常用于大规模高维数据的K邻近查找，可加快欧式聚类的速度，减少聚类所需的时间；②设定距离阈值Dthres，在待分割的点云中随机地选取一个初始点Pstart，创建一个点云集合Ri，将Pstart加入Ri中.依据KD-tree在待分割的点云中搜索初始点Pstart距离阈值Dthres范围内的点集Q={P1,P2,…,Pn}，将其加入Ri中并标记点Pstart.再从Ri中抽取未标记的点P，依据KD-tree在待分割的点云中搜索点P距离阈值Dthres范围内的点集Q={P1,P2,…,Pn}，将其加入Ri中，标记刚才的点P，继续从Ri中抽取未标记的点P重复刚才的步骤直至Ri中不再有新的点加入，此时将Ri作为一个分割完成的目标；③在待分割的点云中再抽取一个未标记的点作为初始点Pstart，重复上述步骤直至待分割的三维点云中的点全部被标记，欧式聚类完成得到相应的聚类目标.

由欧式聚类的原理可知：欧式聚类的效果取决于距离阈值的选取，传统的欧式聚类算法对于距离阈值的选取较为敏感.距离阈值选取过小，可能将同一个目标分割成很多个目标，造成过分割的现象.距离阈值选取过大，如果几个目标的空间位置相距较近，那么有可能将几个不同的目标合并为同一个目标，造成欠分割的现象.上述问题使得在实际的应用中往往很难确定准确的距离阈值.图2为过分割的点云图像，框区域为过分割的目标.图3为欠分割的点云图像，框区域为欠分割的目标.

图2 点云过分割(距离阈值：0.2 m)

图3 点云欠分割(距离阈值：1 m)

3 改进欧式聚类方法

针对传统欧式聚类算法对距离阈值敏感的问题，本文希望通过改进使得欧式聚类算法在一个范围较大的距离阈值区间内都可以有较好的分割效果，从而降低距离阈值选取的难度.以无人车应用为例，欧式聚类距离阈值的可行范围一般在0～1 m，由于激光雷达的分辨率较高，在较小的空间范围内也分布着较多的激光点，在此距离阈值范围内可以满足对相互关联的激光点的搜索.当距离阈值超过1 m时，欧式聚类只能检测空间距离间隔较大的目标，对于空间距离间隔较小的多个目标极易造成目标欠分割的现象.但在0～1 m的可行范围内由于不同目标的尺寸和距激光雷达的距离、角度有所不同，使得获得的点云的稀疏程度也有所不同，以某一选定的距离阈值进行目标聚类时仍然存在某个单目标过分割和几个目标被聚类为同一目标的现象，使得距离阈值的合理选取较为困难.在可行的距离阈值范围内，距离阈值的选取其目的是避免过分割和欠分割的现象，如选取距离阈值较小的一个区间，范围为0～0.5 m，可以避免欠分割的现象，但需要解决将过分割的目标聚合成正确目标的问题.如果选取距离阈值较大的一个区间，范围为0.5～1 m，可以避免过分割的现象，但需要解决欠分割的目标正确分割的问题.由于仅依据空间的距离关系很难准确地将过分割的目标重新聚合，因此本文选取距离阈值较大的区间，即0.5～1 m.同时，在传统的欧式聚类搜索过程中，对聚类目标和干扰目标的激光点设定不同的激光点权值，然后去除搜索过程中干扰目标的激光点，较好地解决了传统欧式聚类在此距离阈值区间内欠分割目标的分割问题.本文首先以一组二维点为例，阐述改进欧式聚类方法的主要思想.

图4a)为一组二维点，其中有三个目标：类A、类B、类C，依据上述的欧式聚类原理，随机的选取这组点中的一个点作为起始点，假设为类A中的某一点，然后开始搜索其距离阈值内的点，再依据搜索到的点搜索距离阈值Dthres内未被搜索过的点，见图4b).当搜索到类A的边缘点时，如果距离阈值过大将会搜索到类B、类C中的点，见图4c)中的点1～6.此时如果再依据点1～6进行搜索，见图4d)，则搜索将会从类A延伸到类B和类C，最终将类A、类B、类C归为同一个目标出现欠分割的情况，见图4e).

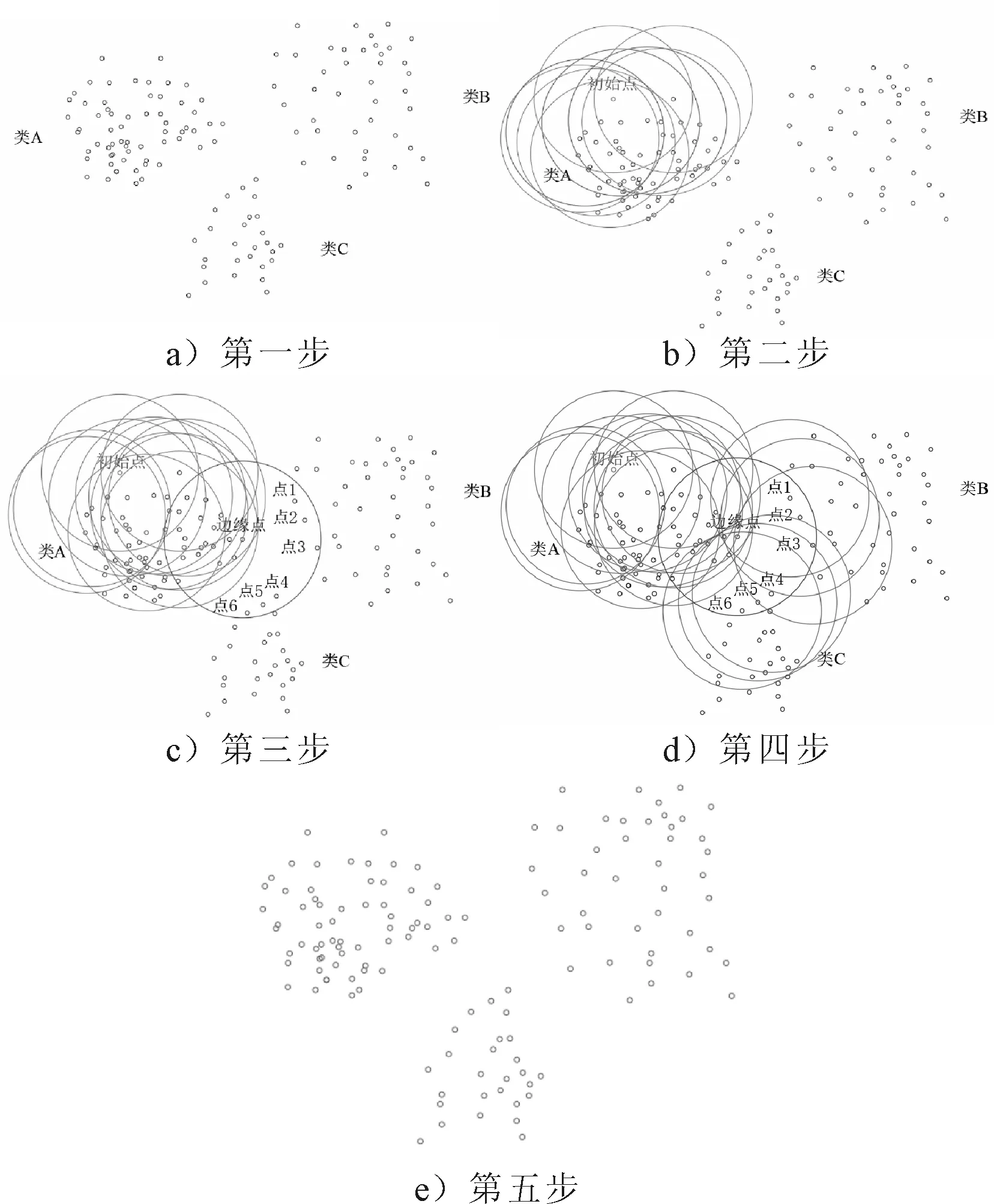
图4 欧式聚类中的欠分割问题

上述的欠分割问题是因为在类A的边缘点处进行搜索时，由于距离阈值过大搜索到了其他类中的点.为解决此问题希望去除在类A的边缘点处搜索到的其他类中的点，即依据图4c)中的边缘点进行搜索后，去除搜索到的点集中的点1～6，不再以其他类中的点继续搜索，阻止搜索从类A延伸到类B和类C.对上述方式单独讨论图4c)中边缘点的搜索和对点1～6的去除，图5为图4c)中边缘点搜索到的点集及点的坐标，其中搜索中心为图4c)中的边缘点.

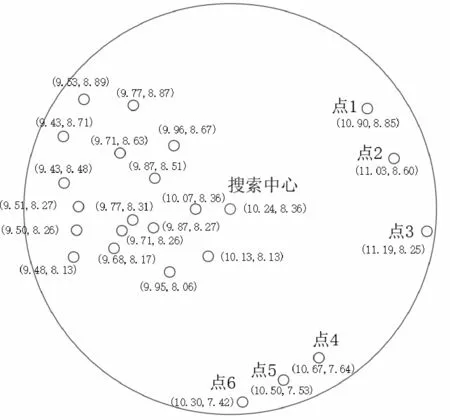
图5 边缘点搜索到的点

依据图5中搜索到的点的坐标计算此次搜索的“类别点”C，其坐标的计算公式为

(1)

(2)

式中：C.x，C.y为“类别点”C的坐标值；n为距离阈值范围内搜索到的点的数量；p0.x、p0.y为搜索中心的坐标值；pi.x，pi.y为距离阈值范围内搜索到的点的坐标值；D(pi,p0)为距离阈值范围内搜索到的点到搜索中心的距离.

计算类别点的目的在于确定边缘点处进行的搜索更倾向于哪个目标，由式(1)和(2)可知，搜索中心附近的点在计算“类别点”C的坐标时所占的比重较大.由于搜索从类A开始，所以搜索中心附近的点以类A中的点居多，其他类中的点距搜索中心较远且数量较少.根据式(1)和(2)计算的 “类别点”的坐标和位置见图6.由图6可知，距离阈值范围内类A中的点距“类别点”的距离比较小且比较均匀，而其他类中的点1～6与“类别点”的距离较远.后续依据距离阈值范围内的点和“类别点”的关系对类A中的点和其他类中的点1～6进行区分.

图6 “类别点”位置及坐标

计算出“类别点”后，将图6中除搜索中心以外的点与搜索中心相连，给每条边赋予一个权值Q，见图7，权值的计算公式为

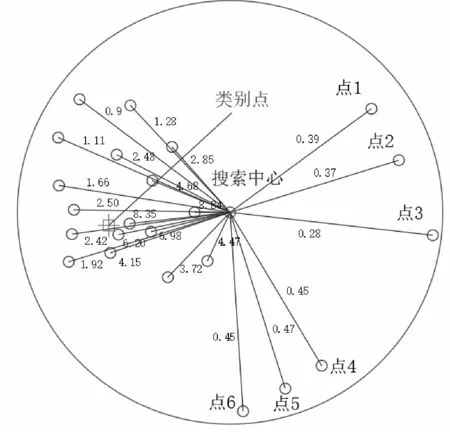
图7 距离阈值范围内各点权值图

(3)

式中:D(pi,p0)为距离阈值范围内搜索到的点到搜索中心的距离；D(pi,C)为距离阈值范围内搜索到的点到"类别点"的距离；D(p0,C)为搜索中心到类别点的距离；Dthres为距离阈值.

由图7可知，搜索中心附近的点其权值较大，且类A中与搜索中心距离较远的点其权值大于其他类中距搜索中心较远点的权值.根据计算得到的权值，其他类中的点1～6被区分了出来，此时依据式(4)计算出截断权值，即权值的均值，然后将大于截断权值的点保留，将小于截断权值的点剔除.

(4)

根据图7其截断权值由式(4)计算得2.9，则点1～6被剔除，最终图4c)中类A的边缘点搜索到的点集中不再包含类B和类C中的点，搜索不会再从类A延伸到其他类.

将上述方法拓展到三维点云的聚类，当在搜索一个目标的过程中搜索到其他干扰目标的激光点时，通过上述方法去除其他目标中的激光点，阻止聚类从一个目标延伸至其他目标，从而较好地解决了在较大距离阈值时产生的三维点云的欠分割现象.类别点坐标的计算扩展到三维空间见式(5)～(7)，各点权值的计算仍为式(3).

(5)

(6)

(7)

由于激光雷达采集到的点云，距离较近处密集，较远处稀疏，因此对式(4)乘一裕度σ来调节截断权值，则截断权值见式(8).在距激光雷达较远处选取一个小于1的σ来降低截断权值，使得距激光雷达较远处的聚类搜索保留更多的点，防止较远处的目标出现过分割的现象.

(8)

改进之后欧式聚类算法流程见图8.

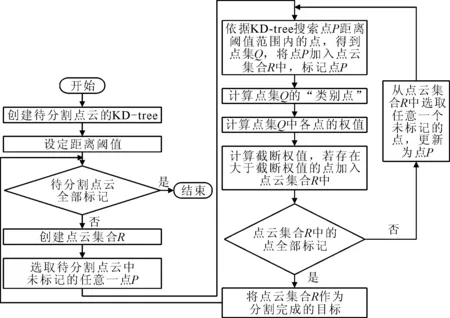
图8 改进后的欧式聚类算法流程图

4 实验结果及分析

针对上述改进之后的欧式聚类算法，以无人车实际采集的三维点云数据为研究对象，通过在较大的距离阈值区间选取不同的阈值对传统的欧式聚类算法和改进之后的欧式聚类算法进行了对比和分析.其中，距离阈值区间设置为0.5～1 m，并分别选取了0.5，0.7，1 m三个距离阈值.图9为聚类前的点云图像，图10～12分别为距离阈值取0.5，0.7，1 m时的点云聚类情况.

图9 聚类前的点云图像

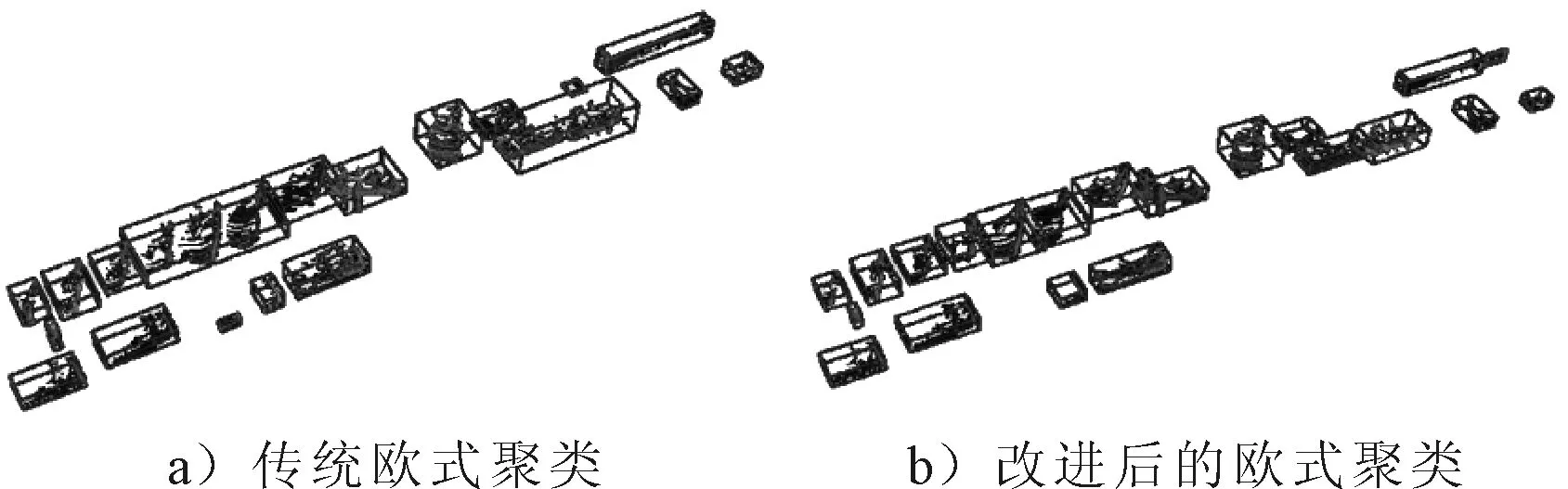
图10 距离阈值为0.5 m的聚类结果

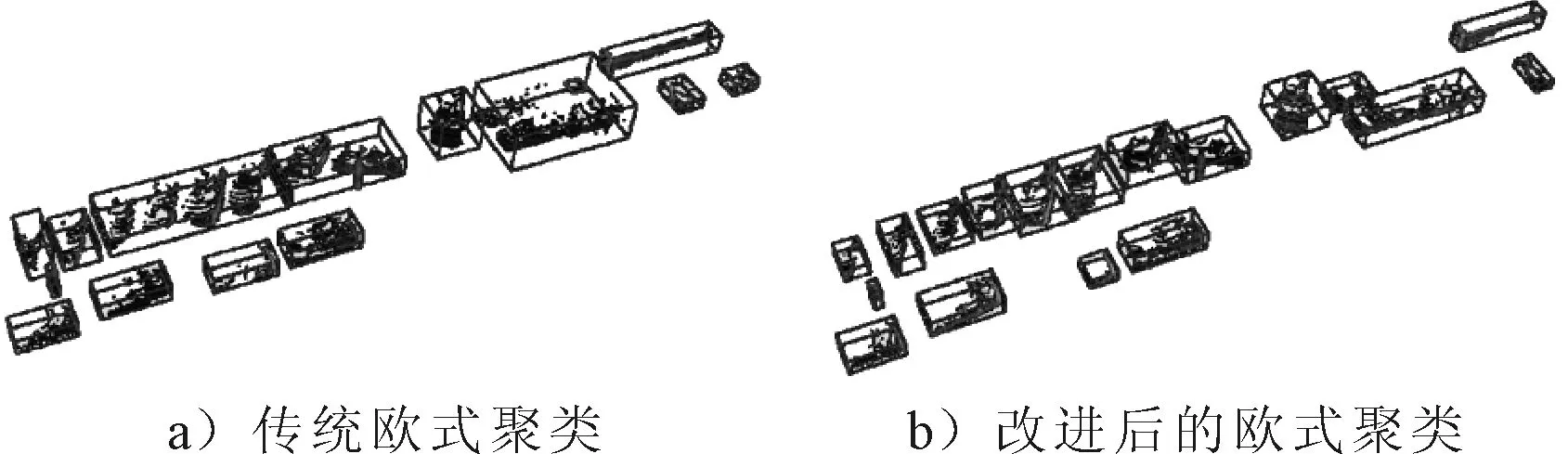
图11 距离阈值为0.7 m的聚类结果

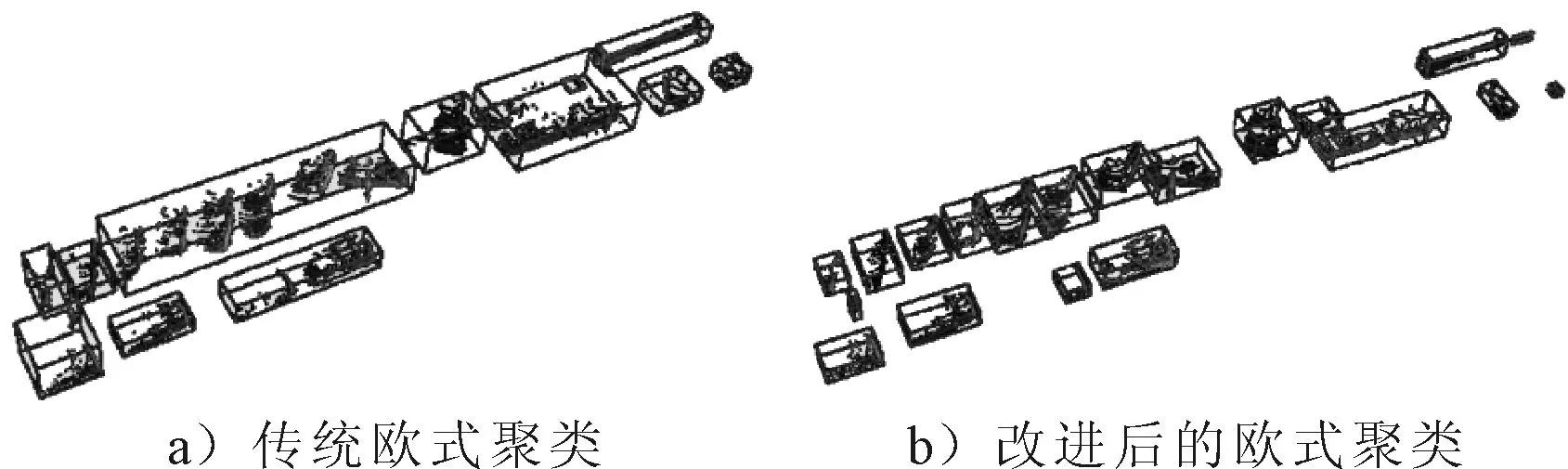
图12 距离阈值为1 m的聚类结果

由图10～12可知，当多个目标相距较近时，距离阈值选取较大会出现很多欠分割的目标，随着距离阈值的增大欠分割的现象更加严重.相较于传统的欧式聚类算法，改进后的算法在0.5～1 m的距离阈值范围内都可以较好地分割距离较近的多个目标，在一定程度上解决了传统欧式聚类对距离阈值敏感的问题，降低了距离阈值选取的难度.实验中对传统的欧式聚类算法和改进之后的欧式聚类算法进行了连续帧点云的目标检测，其平均结果见表1～3.

表1 距离阈值为0.5 m 单位：%

表2 距离阈值为0.7 m 单位：%

表3 距离阈值为1 m 单位：%

由表1～3可知，在0.5～1 m的距离阈值区间内改进后的欧式聚类较传统的欧式聚类其正确率都有一定提高，在距离阈值选取0.5，0.7，1 m时改进后的欧式聚类较传统的欧式聚类其正确率分别提升6.5%，13%，26.5%且正确率都较高，而欠分割率有较大的下降，其欠分割率分别下降9%，17%，31%.同时改进后的欧式聚类在0.5～1 m的距离阈值区间内过分割率和丢失率都较低.表4为单帧点云聚类的平均耗时，从平均耗时来看改进后的欧式聚类较传统的欧式聚类耗时有所增加，但耗时增加幅度不大，依旧可以满足实时的目标检测.综合聚类效果和耗时来看，改进后的欧式聚类算法较传统的欧式聚类算法在一个距离阈值区间内都有较好的聚类效果，降低了传统欧式聚类距离阈值选取的难度.

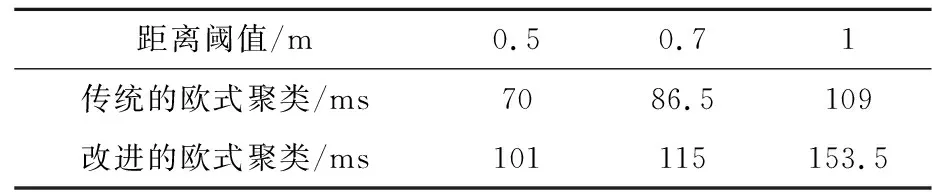
表4 单帧点云聚类的平均耗时

5 结 束 语

文中以无人系统中的三维点云聚类方法为研究对象，针对传统欧式聚类对距离阈值敏感，易造成聚类目标过分割或欠分割的问题，选取了范围较大的大距离阈值区间，避免了聚类中的过分割现象.同时，为了去除搜索过程中搜索到的其他目标的激光点，提出了一种改进后的欧式聚类算法，较好地解决了选取大距离阈值时造成的欠分割现象，使得改进之后的欧式聚类在一个较大范围的区间内都有较好的聚类效果，在选取的可行距离阈值区间内解决了传统欧式聚类对距离阈值敏感的问题，降低了距离阈值选取的难度.通过与传统欧式聚类的对比，验证了改进后算法的有效性和合理性.尽管以无人车点云数据作为研究对象，但是文中的方法可以很容易扩展到机器人、无人船等领域.