基于去奇异边界元法的二维数值波浪水池计算参数影响分析

杨师宇 吴静萍 汪 敏* 陈昌哲

(武汉理工大学船海与能源动力工程学院1) 武汉 430063)(上海交通大学船舶海洋与建筑工程学院2) 上海 200240)

0 引 言

对于预报波浪与结构物的相互作用，随着计算机和数值模拟技术的发展，建立数值波浪水池(numerical wave tank，NWT)进行数值模拟试验是一种重要的研究手段.

早期，数值波浪水池技术忽略流体黏性，流动无旋，基于势流理论，采用Green函数方法[1-2]或高阶谱(higher-order spectral, HOS)方法[3]求解Laplace方程的初边值问题，自由面捕捉技术从线性、弱非线性发展到强非线性、完全非线性，自由面边界条件非线性问题一直是提高计算波浪运动问题精度的关键.忽略流体黏性的波浪运动计算方法，除了求解Laplace方程的边值问题之外，还引入人工涡黏模型的非静压模型浅水方程方法[4-5]、Boussinesq 水波方程方法[6-7]和适用于强非线性波浪问题的层析波浪理论(green-naghdi理论)方法[8-9].

随着CFD(computational fluid dynamics)的发展，考虑流体黏性，求解黏性流体运动的N-S(Navier-Stokes)微分方程，采用VOF(volume of fluid)等方法捕捉自由面，实现了强非线性的波浪流动的模拟[10-11].由于微分方程常用差分方法、有限元方法或有限体积法等方法离散求解，波浪问题需做非定常计算，计算量大且耗时.虽然粘-势流耦合模型[12]有效提高了计算效率，但是还是相当耗时.虽然波浪与小尺度构件相互作用黏性的影响比较重要，但是在处理波浪与大尺度结构物相互作用的问题中，流体的黏性往往被忽略，所以势流理论在大尺度的波固耦合问题中仍然在发展和使用.

基于势流理论的数值计算方法，发展较早的是采用Green函数在流场边界布置源汇分布的边界元方法.其按照是否考虑流动随时间的变化，分为频域和时域两大类方法.相对于频域方法对弱非线性、周期性问题有效的局限性而言，时域方法应用范围更加广泛.按照求解的积分方程是否具有奇异性，又出现奇异边界元方法和去奇异边界元方法.奇异边界元方法发展了高阶边界元法(higher-order boundary element model,HOBEM)[13]和泰勒展开边界元法(taylor expansion boundary element method，TEBEM)[14]以降低处理奇异积分的难度.去奇异边界元方法(desingularized boundary integral equation method，DBIEM)最早由Cao等[15]提出，随后的30多年来，相继被应用于求解与波浪运动相关的问题[16-19].

去奇异边界元方法将源(汇)分布移至流域边界之外，从而解决了边界积分方程的奇异问题.与奇异常值边界元方法相比，去奇异边界元法在形状突变处的计算精度得到了提高[20]，编程与计算的效率也高[21].但是去奇异边界元法的计算精度对去奇异距离的变化较为敏感，且去奇异距离在不同问题中的最佳取值不尽相同.除此之外，源点数量、时域计算时的时间步长，在不同问题中的取值也对计算精度影响较大.

文中采用Cao等[22]的时域DBIEM构建了一种二维数值波浪水池.自由面边界条件考虑了弱非线性，采用混合欧拉-拉格朗日法追踪瞬时自由面流体质点，采用四阶Adams-Bashforth-Moulton(ABM)预测-校正法对下一时间步的波面抬高与自由面速度势进行更新.同时，采用人工阻尼层(damping layer)避免水池尾端壁面的反射，采用斜坡函数(ramp function)避免造波入口处水流速度变化过快造成的计算不稳定，采用非均匀布点的Chebyshev五点光顺法[23]对自由面上的速度势以及波面进行光顺，避免锯齿状不稳定现象(saw-tooth instability).将文中构建的数值波浪水池的数值计算波形与二阶Stokes波解析解进行对比，依次探讨了源点数量、去奇异距离以及时间步长对计算精度的影响，并综合考虑计算精度与计算效率，给出了计算参数建议值.

1 数学模型

二维数值波浪水池示意图见图1，建立笛卡尔坐标系oxz，坐标原点o位于静水面与造波入口面的交点处，ox水平向右，oz竖直向上，图1中h为水池静水深；V为流域；造波入口面、自由面、尾端壁面和水底壁面四个流域边界分别为ΓU，ΓF，ΓD，ΓB；xu为人工阻尼层起始端点的x轴坐标；Ldl为人工阻尼层的长度.

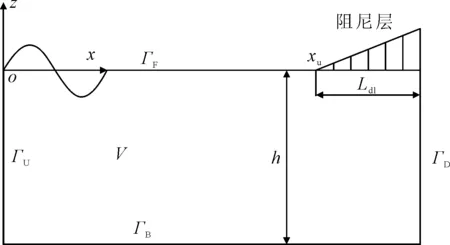
图1 二维数值波浪水池示意图

假定流体为理想流体且其运动无旋，则可采用势流理论来描述水池内的水体运动，其边界条件与初始条件为

2φ=0，inV

(1)

(2)

(3)

(4)

(5)

φ=0，ast≤0，onΓU&ΓF&ΓD&ΓB

(6)

η=0，ast≤0，onΓF

(7)

式中：φ(x,z,t)为速度势；n=(ni,nk)为流域边界外法线方向的单位向量；η(x,t)为自由面上的波面抬高；g为重力加速度；ρ为流体密度；pa为自由面上的大气压力，假定恒等于0；φU(x,z,t)为造波入口面的输入速度势；Rm(t)和vu(x)分别为斜坡函数与阻尼系数.

(8)

(9)

式中：Tm为斜坡函数的作用时间，文中取值为2倍的入射波周期；ω为入射波角频率；α为控制参数，用于控制阻尼层的阻尼强度，参照文献[19]取1，阻尼层长度Ldl至少为1倍波长，参照文献[17]取1倍入射波波长；xu相应取尾端壁面前端1倍波长位置的x轴坐标.

2 数值方法

2.1 去奇异边界元法

去奇异边界元法将原本位于流域边界上的源点移至流域外一定距离，即将积分表面Sd移到流域V外，以保证源点和配置点不重合，从而避免奇异性，示意图见图2.

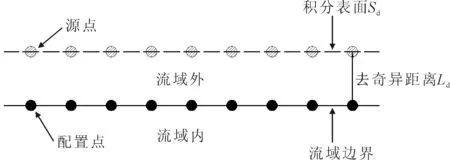
图2 源点与配置点示意图

去奇异边界元法分为直接法与间接法，直接法直接运用格林第二定理.本文采用间接法，流域内任意点的速度势为积分表面上源点对该点引起的速度势的线性叠加，表示为Rankine源形式.

(10)

式中：q=(xq,zq)为流域中的任意点(包括流域边界上的配置点与流域内的场点)坐标向量；p=(xp,zp)为流域外的源点坐标向量；σ(p)为对应源点的源强；G采用简单格林函数，对于该二维问题，G(p,q)可定义为

G(p,q)=ln|p-q|

(11)

对于式(8)中的源强，需运用已知的边界条件来求解.应用相关边界条件，用来求解未知源强度的去奇异化边界积分方程为

(12)

(13)

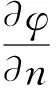
配置点与源点一一对应，两个对应点之间的距离称为去奇异距离Ld，为

Ld=ld(Dm)β

(14)

式中：ld和β为常数；Dm为局部网格尺寸，一般取网格大小的平方根，以源点代替网格，网格大小取自由面处源点之间的距离乘以造波入口面处源点之间的距离.其中ld和β对计算精度影响很大，后文中将对这两个系数对计算精度的影响进行研究.

2.2 混合欧拉-拉格朗日法

为了追踪流体微粒在瞬态自由面上随时间的变化，将欧拉形式下的自由面运动学边界条件式(3)及动力学边界条件式(4)转换为拉格朗日形式，其转换方法为采用随体导数.

(15)

式中：v为瞬态自由面上流体微粒的运动速度.

将式(13)代入自由表面边界条件式(3)与式(4)，自由面边界条件可改写为如下形式.

(16)

(17)

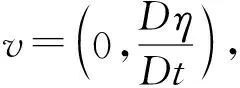
(18)

(19)

2.3 四阶Adams-Bashforth-Moulton预测-校正法

(20)

(21)

式中：Δt为时间步长.

然后将四阶Adams-Bashforth方法中得到的预测值代入隐式四阶Adams-Moulton公式中进行校正，最终得到η与φ的校正值.

(22)

(23)

四阶Adams-Bashforth-Moulton预测-校正法还需要前四个时间步的波面抬高与自由面速度势才能自启动，其中第一个时间步的波面抬高与自由面速度势已由初始条件式(6)与式(7)给出，其他三个时间步的波面抬高与自由面速度势的计算表达式为

ηt+Δt=Δt·ft

(24)

φt+Δt=Δt·gt

(25)

3 计算参数对数值计算结果的影响

建立二维数值波浪水池，水池静水深h为0.6 m.目标波形的参数分别为波长L=1 m，波高H=0.03 m，周期T=0.801 1 s.

取数值波浪水池中x1=L与x2=4L两个监测点，通过将两个监测点的稳定波形与二阶Stokes波解析解进行比较，来分析计算参数对数值计算结果的影响，稳定波形取15T～18T时间段.讨论的计算参数包括源点数量、去奇异距离和时间步长，其中源点数量又包括自由面单位波长距离的源点数量nx和造波入口面的源点数量nz，去奇异距离又包括常系数β和ld，时间步长用Δt表示.计算参数的初始取值参照文献[17]，取nx=60，nz=30，β=0.5，ld=0.5，Δt=T/100.

一般来说，判别水池中生成波形的精度，应从波高、波长和周期三个方面进行综合评估，然而经过预计算，在本文的计算参数取值范围内，所得波形的平均波长和平均周期均与解析解相近，误差小于1%，因此后文仅讨论波高在不同计算参数下的精度.为更为直观地观察波高与解析解之间的误差，定义x1监测点处稳定波形的平均波高为H1，与解析解波高H之间的相对误差δ1为

(26)

定义x2监测点处稳定波形的平均波高为H2，与解析解波高H之间的相对误差δ2为

(27)

为计量波高沿传播方向的变化，定义x1监测点与x2监测点之间稳定波形的平均波高相对变化δ3为

(28)

由式(12)可知，去奇异距离同时受源点数量nx、nz、常系数β和常系数ld的影响，后文先讨论源点数量对计算精度的影响，确定了合适的源点数量后再讨论两个常系数的影响.

3.1 源点数量的影响

改变自由面单位波长距离的源点数量nx，分别取nx=20，40，60和80.图3为不同nx时x1与x2监测点的波面时历曲线，表1为nx对波高的影响.由图3和表1可知，当源点数量nx在40～80之间时，x1与x2监测点的波高相对误差δ1与δ2均在1%左右，波高相对变化δ3均在1%以下，nx为20时，x1监测点的波高相对误差δ1小于1%，但波高沿传播方向的损失较严重，波高相对变化δ3达到了11%.选取源点数量nx=40.

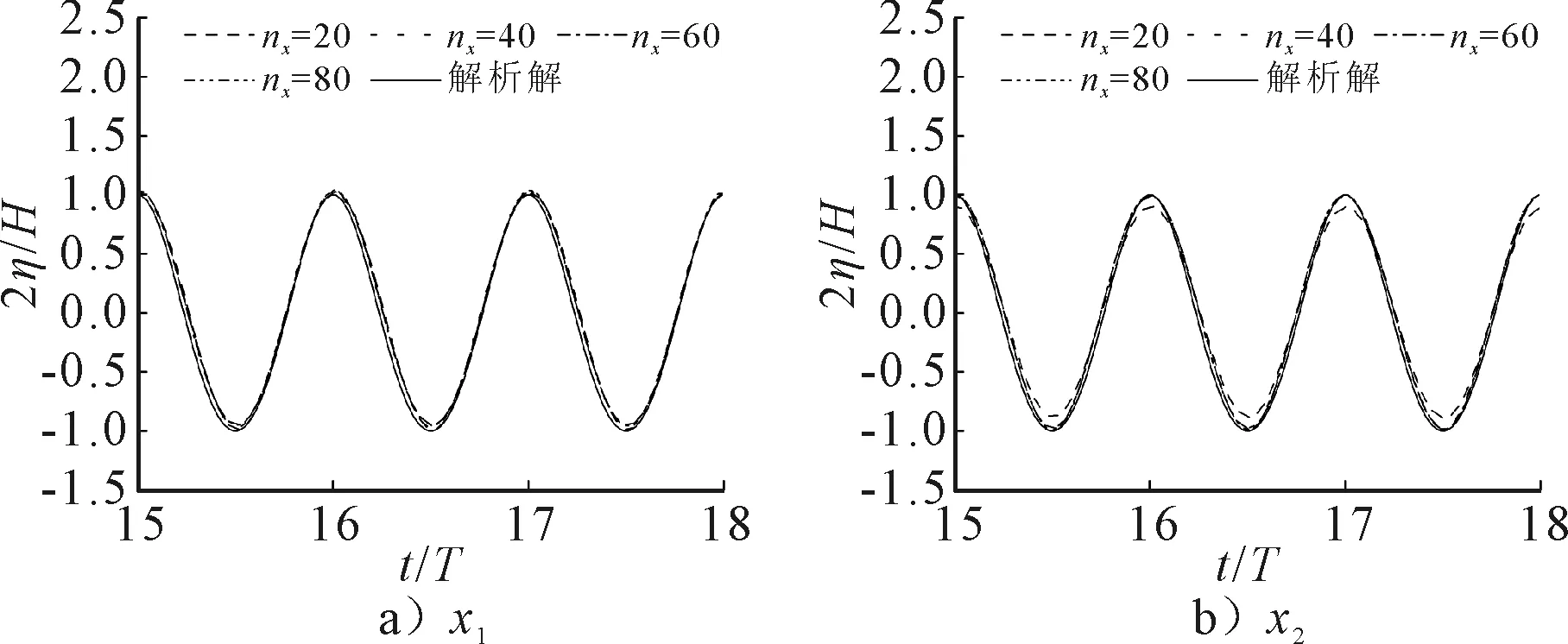
图3 x1与x2监测点的波面时历曲线

表1 nx对波高的影响

取上文中建议的源点数量nx=40，改变造波入口面的源点数量.由于两个边界交点处的边界条件无法确定，本文在边界交点处均未布置源点，同时为了确保自由面附近的计算精度，在接近自由面与造波入口面交点的位置z=-H位置在造波入口面额外增加了一个源点，因此造波入口面源点的布点方案为在z轴坐标(-h,-H]的区间内均匀布点，数量分别取nz=2，3，4，6，8和10.由于x1与x2监测点的波形几乎相同，因此图4为不同nz时x1监测点的波面时历曲线，表2为nz对波高的影响.由图4和表2可知，z方向的源点数量nz并非越大波形精度就越高，当源点数量nz在2～10时，数值水池生成波浪的波高相对误差δ1与δ2均小于2%，波高相对变化δ3小于1%.选取源点数量nz=3.

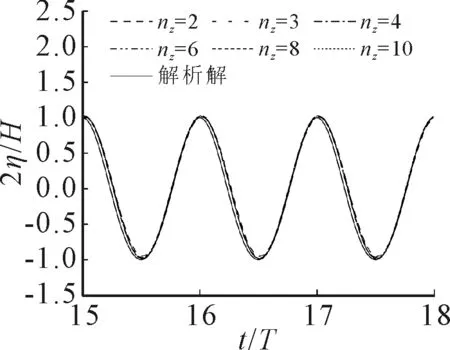
图4 x1监测点的波面时历曲线

表2 nz对波高的影响

鉴于上文中造波入口仅需布置少量的源点，就能得到足够精度的结果，对造波入口处源点的z轴位置对波形精度的影响进行补充研究.仅在入口布置单个源点，分别取z=-H，z=-(h+H)/2和z=-h，所得的x1监测点波面时历曲线见图5.由图5可知，自由面附近，即z=-H处的源点对计算结果的精度影响很大，其单个源点所生成的波形已与解析解相差较小，而与自由面距离较远的源点所生成的波形与解析解相差很大，上文中入口源点均包含了z=-H处的源点，这也是造波入口仅布置少量源点就能获得足够波形精度的主要原因.

图5 x1监测点的波面时历曲线

3.2 去奇异距离的影响

取上文中建议的源点数量nx=40，源点数量nz=3，改变参数β，分别取β=0.4，0.5，0.6，0.7，0.8，0.9和1.0.由于x1与x2监测点的波形几乎相同，图6为不同β时x1监测点的波面时历曲线，表3为β对波高的影响.由图6和表3可知，当参数β在0.4～1.0时，波高相对变化δ3均小于1%，且参数β与波高相对误差δ1与δ2的关系较复杂，当β=0.5和0.8时，波高相对误差δ1与δ2最小，当β=0.4，0.7，0.9和1.0时，波高相对误差δ1与δ2大于2%.当β<0.4时，源点与配置点过近，边界积分方程接近奇异，计算结果误差过大或计算无法进行，因此并未给出β<0.4时的计算结果，综上选取参数β=0.5.

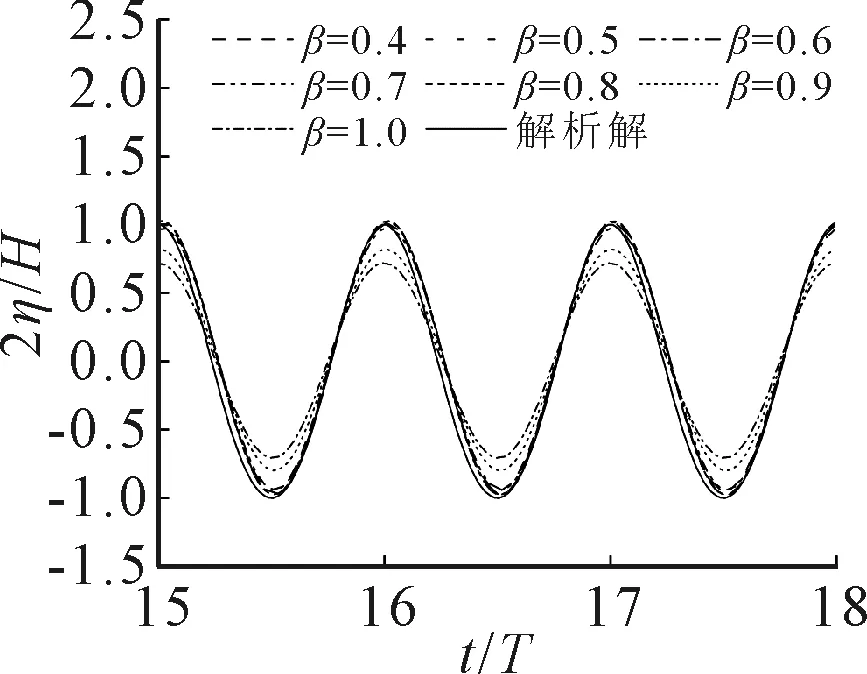
图6 x1监测点的波面时历曲线

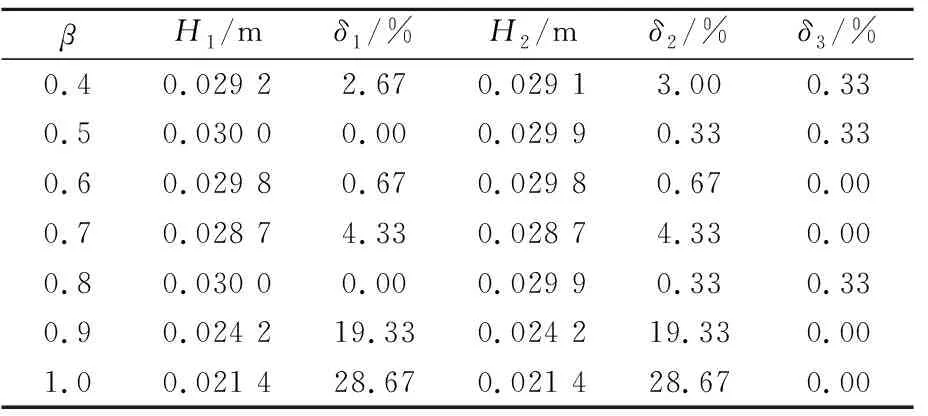
表3 β对波高的影响

取上文中建议的源点数量nx=40，源点数量nz=3，参数β=0.5，改变参数ld，分别取ld=0.4，0.5，0.6，0.7，0.8，0.9和1.0.由于x1与x2监测点的波形几乎相同，图7为不同ld时x1监测点的波面时历曲线，表4为ld对波高的影响.由图7和表4可知，当参数ld在0.4～1.0时，波高相对变化δ3均小于1%，且参数ld与波高相对误差δ1与δ2之间的关系较复杂，当ld=0.5和1.0时，波高相对误差δ1与δ2最小，当β=0.7，0.8和0.9时，波高相对误差δ1与δ2大于2%.当ld=0.3时，波高相对误差δ1与δ2在4%左右，ld<0.3时，源点与配置点过近，边界积分方程接近奇异，计算结果误差过大或计算无法进行，因此并未给出ld<0.4时的计算结果，综上选取参数ld=0.5.

图7 x1监测点的波面时历曲线

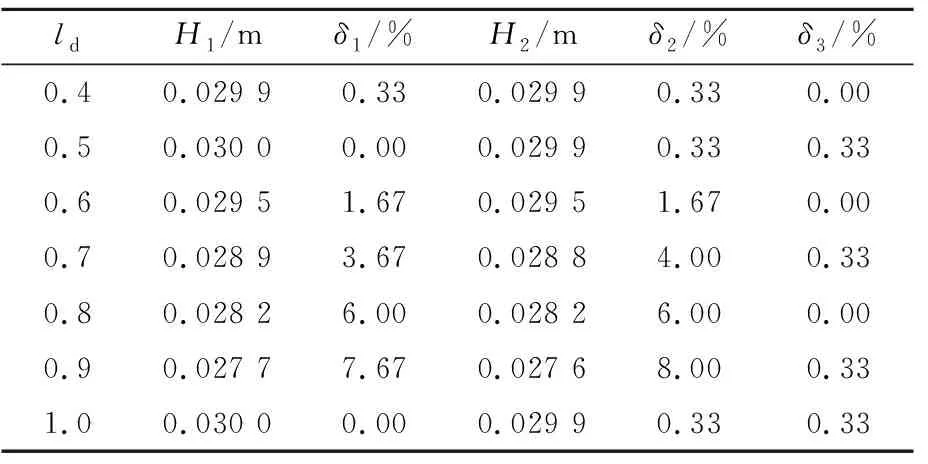
表4 ld对波高的影响

3.3 时间步长的影响

取上文中建议的源点数量nx=40，源点数量nz=3，参数β=0.5，参数ld=0.5，改变时间步长Δt，分别取Δt=T/50，T/75，T/100，T/125和T/150.由于x1与x2监测点波形几乎相同，图8为不同Δt时x1监测点的波面时历曲线，表5为Δt对波高的影响.由图8和表5可知，当时间步长Δt在T/150～T/50时，波高相对误差δ1与δ2以及波高相对变化δ3均小于1%.时间步长越大，计算效率越高，综上选取时间步长Δt=T/50.

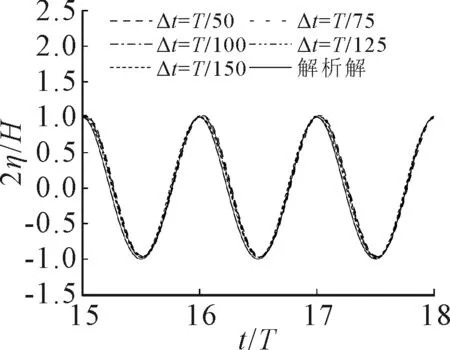
图8 x1监测点的波面时历曲线

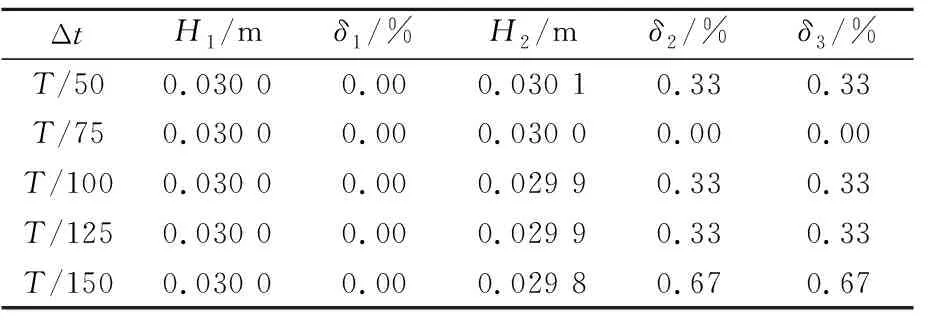
表5 Δt对波高的影响

4 结 论

1) 构建的数值波浪水池对二维弱非线性计算有足够的精度，为后续研究水面式防波堤的水动力性能问题奠定基础.

2) 造波入口面的源点数量nz取3.造波入口处的源点中，距离自由面较近的源点对计算精度影响很大，在造波入口设置源点时应至少在自由面附近布置一个源点，否则将产生较大计算误差.

3) 源点数量中，自由面单位波长距离的源点数量nx取40，时间步长Δt取T/50，有足够的计算精度同时兼顾了计算效率，其对应的CFL数为0.8，实际计算中为保持计算稳定，应使CFL数≤0.8.

4) 去奇异距离中，建议参数β取0.5，参数ld取0.5.参数β与ld对计算精度影响很大，且两个参数与计算精度之间的关系比较复杂，在计算中应慎重取值.当β为0.5与0.8，ld为0.5与1.0时，计算精度最高