拉普拉斯变换在卡方分布中的应用
刘芝秀,赖伊清
拉普拉斯变换在卡方分布中的应用
刘芝秀,赖伊清
(南昌工程学院 理学院,江西 南昌 330099)
本文利用拉普拉斯变换作为概率分布的特征函数,重新导出了卡方密度函数, 并给出了计算卡方分位数的一种新算法,该算法可用于计算自由度为4的任意卡方分位数,基于自由度为4的任意卡方分位数的计算进而改进了教学评估的一种手段,即提高了五等级评价标准下学生成绩占比异常情况的抽检效率。
拉普拉斯变换; 卡方分布; 卡方分位数; 自由度; 教育质量评估

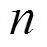
本文即基于这一思考,用拉普拉斯变换作为分布函数的特征函数,同时给出了计算自由度为4的任意卡方分位数的算法,并进而应用它缓解了教学管理与评估过程中关于提高五等级评价标准下学生成绩占比异常情况抽检的效率问题。
1 技术预备
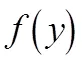

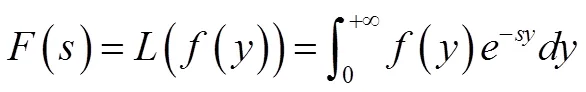
利用拉普拉斯变换的性质可以很方便的计算如下两个常见函数的拉普拉斯变换。


接下来是本文还需要的拉氏变换的卷积定义与性质、唯一性性质和积分性质。




2 卡方密度函数的证明
有了以上的准备就可以用新的方法重新推导卡方密度函数。



而由(2.1)式可得

又根据性质2.1知
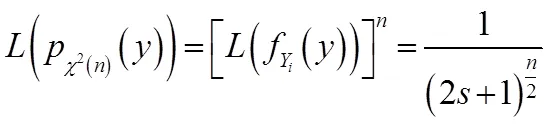
3 卡方分位数的计算
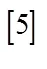
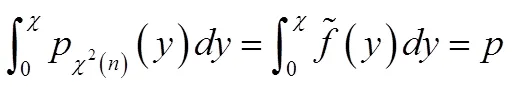
由性质2.3知
即
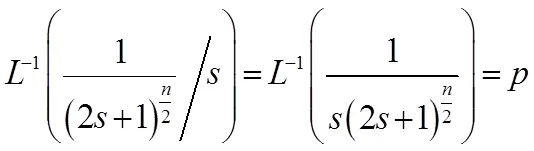

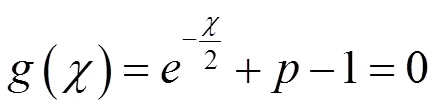


4 在教学评估技术中的应用
下面指出上述内容在教学管理与评估过程中的应用。教育的方式和内容需要与时俱进的稳步改革与创新才能保持其先进性,例如面对新工科人才培养目标,协同开展 STEM 教育就是一个值得探索尝试的教学模式[6];在新冠疫情的影响下,采用线上教学,提高教学的信息技术水平,设计好线上教学对保证教学质量显得尤其重要[7];在“课程思政”理念的引领下,如何将思政元素恰当的融入课堂教学在为国家培养优秀人才方面具有深远意义[8]。另一方面,在教学改革和实践过程中不能离开对教育教学质量的管理与评估[9-10],通常教学管理与评估部门会根据往年的教学情况和当年的教学质量目标,制定一个内部的教学质量监测标准,从而可以采取科学合理的检查与督导行动。教学质量的评估仍然以课程考核为最基本的手段,经验事实告诉我们,学生的成绩总是参差不齐,但具有一定的统计规律性,考试题目缺乏区分度、教师的教学工作不到位、学生的学风较差等等因素都会造成学生成绩分布与正常预期目标分布有较大的偏差。教学管理与评估部门面对着众多的待检课程,但却又仅有较少的专家力量能够进行课程考核和教学质量的检查与督导,有限的专家资源应该重点投放到哪些课程的检查和督导之中就成了一个首先要解决的问题,自然的,应将专家力量重点投放到学生考核成绩占比异常的课程之中。
操作实验如下:
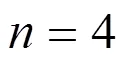
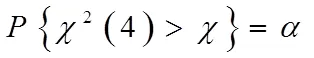
表1 常见卡方分布表 (此处)
仅在卡方分布表所给的分位数下,可能出现要么全部课程都通过检验,要么全部课程都通不过检验,而这一技术问题正可利用前面提出的任意分位数计算方法进行解决。
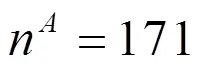

表2 课程A卡方统计量计算结果
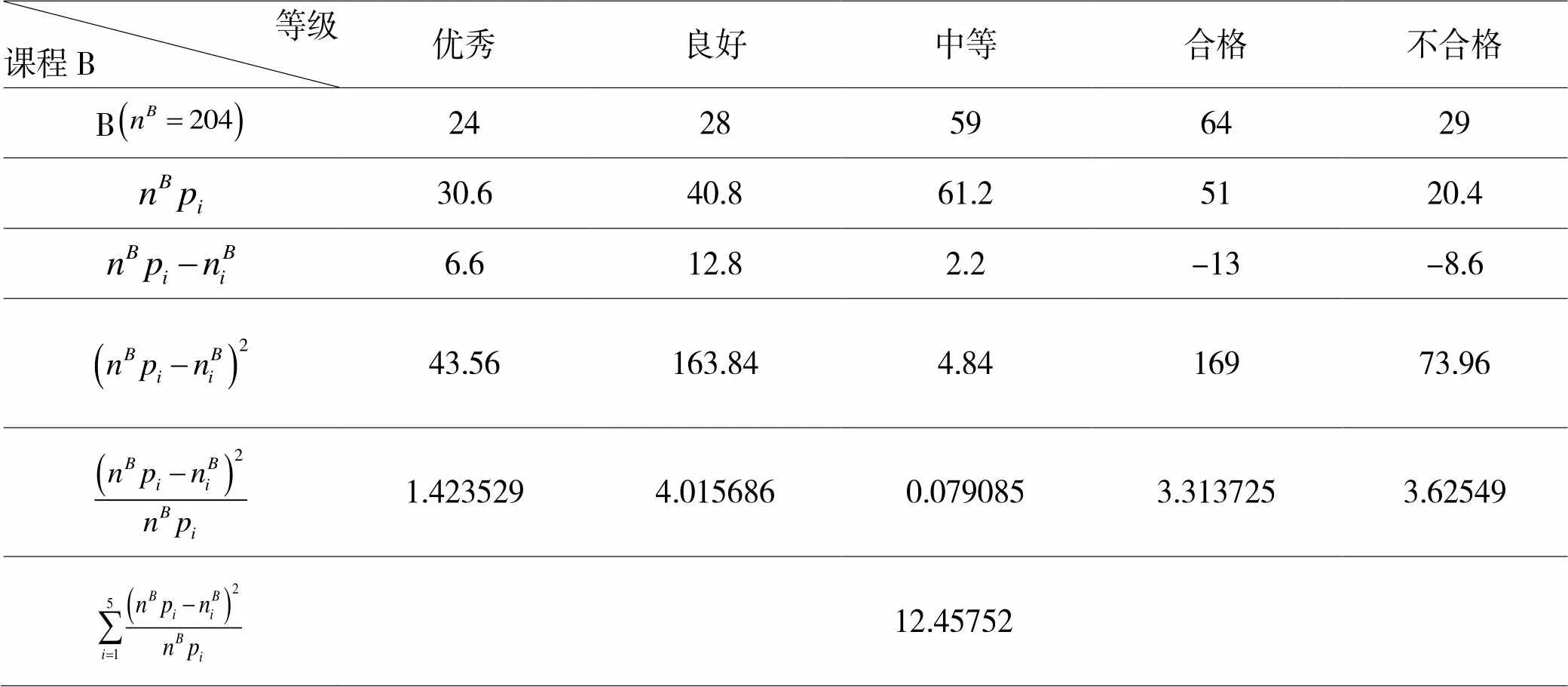
表3 课程B卡方统计量计算结果

表4 课程C卡方统计量计算结果
import math
x=0.5 #x为牛顿迭代法的初始点,运算的最终结果为分位数

for i in range(1,100): #此处循环100次,可以修改循环次数或用误差控制循环次数x=x-((x/2+1) *(math.e**(-x/2))-a)/((-x/2)*(math.e**(-x/2))) #牛顿迭代公式print(x)

表5 补充的卡方分布表(含常见卡方分布表不能查阅的分位数)
根据表2至表5可知,在置信水平为98%的情况下可以认为课程A和C符合预期估计,课程B明显不符合预期;在置信水平为85%的情况下可以认为课程C符合预期估计,课程 A和B不符合预期;在置信水平为75%的情况下可以认为课程A、B、C均不符合预期估计。相应的决策是,如果只有一组专家可以只检查课程B,如果有两组专家可以检查课程 A和B,如果有三组专家则可以检查课程A、B、C。
学生成绩占比异常检验采用更多分组仍然可行,不同的只是卡方检验统计量的自由度,上述方法仍然是实际有效的。当然确定重点检查课程的具体方法有多种,甚至可以直接对卡方统计量大小进行排序而得,统计量越大的课程越应该被重点检查和督导,但习惯上我们希望给出一个较全面的回答,即在一定置信水平下所采取的行动,这样更加量化了教学管理行为的科学性。
[1]茆诗松,王静龙,濮晓龙.高等数理统计(第2版)[M].高等教育出版社,2006:30-33,228-232.
[2]李贤平,陈子毅.概率论基础学习指导书[M].高等教育出版社, 2020:150-151,394-400.
[3]黄小杰,刘芝秀,李运通.普里瓦洛夫关于全纯函数唯一性的问题[J].纯粹数学与应用数学, 2020, 36(4):482-487.
[4]叶其孝,沈永欢.实用数学手册[M].科学出版社, 2006:632-637,648-650.
[5]陈刚,王梦婕.卡方分布密度函数与分布函数的渐近展开[J].南京师大学报(自然科学版), 2014, 37(3):39-43.
[6]赵慧臣,陆晓婷,马悦.基础教育,高等教育,企业以及教育管理部门协同开展STEM教育——美国《印第安纳州科学,技术,工程和数学(STEM)行动计划》的启示[J].电化教育研究,2017 (4):115-121.
[7]苏永美,刘白羽,范玉妹. 高等数学在线教学的设计与实践[J].大学数学, 2021, 1(37):22-26.
[8]张若军,高翔.哲学视域下的高等数学“课程思政”[J].大学数学, 2021, 2(37):13-17.
[9]冯燕茹,林尤武.基于模糊综合评判的大学数学考核方式改革[J].大学数学,2021, 1(37):39-44.
[10]郑浩,王者鹤.美国本科STEM教育质量监测:逻辑,标准与启示[J].中国高教研究,2019(11):55-60.
O177.6
A
1672-1047(2021)06-0131-04
10.3969/j.issn.1672-1047.2021.06.34
2021-11-01
江西省教育厅科技项目“正规族和整函数动力系统”(GJJ180944);江西省教育厅科技项目“层次分析法经验矩阵的一致性检验与调整及其应用研究”(GJJ190963);江西省高校人文社科项目“应用型本科院校学生学习力培养策略研究——基于STEM教育视角”(JY18233)。
刘芝秀,女,四川自贡人,硕士,讲师。研究方向:应用数学。
[责任编辑:张克新]

