感染免疫理论的软件可测试性计算模型

殷 脂

(上海电力大学 计算机科学与技术学院, 上海 200090)

软件的可测试性是指软件测试过程中,在给定的若干组输入条件下,能够发现错误的概率。对软件可测试性的研究有助于确定软件需要测试的程度,并以最合理的方式分配测试资源,设计测试策略,提高测试效率。此外,在软件开发生命周期的早期阶段,可测试性分析还可以为软件结构的设计过程提供指导,从而降低测试成本,提高测试的可行性,进而提高软件的可靠性。

本文结合随机图理论,首先描述了面向对象的扩展软件可测试性模型;然后基于扩散感染免疫理论建立了软件随机图模型;最后给出了软件的可测试性形式化表达,并提出了计算方法。

1 扩展的基于故障/失效模型的PIE技术

1.1 可测试性分析方法

从国际学术论文的理论角度来说,可测试性分析方法主要分为以下4种。

(1) 主要根据某一类流图计算出图中的各类结构信息(结点、边、环等),独立于所选择的测试策略以及程序的执行,并利用测试结果对软件的关键测试部分进行识别和改进[1]。

(2) 基于信息论和信息流图,根据模块的输入输出信息,对模块的可控性和可观测性进行定量计算,以确定模块的可测试性。

(3) 以PIE(Propagation analysis,Infection analysis and Execution analysis)技术为基本原型,分析程序的某个位置,计算其故障检测概率,以反映可测试性。

(4) 基于UML类图的面向对象软件分析技术,主要利用UML类图作为分析对象,通过掌握类之间复杂的依存关系来分析可测试性,并进一步改进UML类图以提升软件的可测试性。

1.2 基于故障/失效模型的PIE技术分析

根据VOAS M[2]提出的故障/失效模型,软件失效只有在以下3个条件都发生时才会产生:输入引起故障执行;故障导致了错误的数据状态;数据状态进而传导至输出状态,使得用户获得非预期的结果。本文结合面向对象软件的特征,以PIE技术为基础原型,并将PIE技术中的位置概念扩展为对象,构造软件测试的故障/失效模型。

PIE技术的基础模型及简单分析如下。

(1)P表示若数据状态更改不正确,则该更改将影响程序输出的概率。在估算P值时,对跟踪语句中的变量进行赋值,以便在后继执行中使用,直至到达输出结点,并记录全部语句。这些语句的I值乘积即为P值。如果无法到达输出节点,则P值为零。

(2)I表示如果程序的一部分发生了变化,那么这种变化将错误地改变数据状态的概率。对于输入或输出语句,I通常设置为1;表达式语句有更复杂的I计算规则,根据所包含的操作符、变量和常量的数量和类型,每一个元素都有自己的I值,通过加权平均计算后获得该条语句的I值。当常量作为操作数时,I的值为1;当变量作为操作数时,I值为这一变量所在的最后一条语句I值。

(3)E表示在假设输入是均匀分布的情况下,程序的某个部分被执行的概率,上限是1。顺序结构语句的E值为1,因为它们通常均被执行;另一方面,通常必须对分支语句进行评估,以确定它们是否被执行,或者用整体平均值来代替[2-3]。

1.3 扩展至软件对象粒度级上的PIE模型

基于PIE技术原型,在本文的扩展模型中,将软件系统的对象抽象为可测试性的位置概念,修改基本模型中的检测粒度,并给出3个假设前提。

假设1I的取值范围为[0,1]。对于一个对象,每一对输入/输出都有相应的I值。这与对象内部的处理逻辑相关,一般来说,对象越复杂,越有可能隐匿故障。E的取值范围为[0,1],其值是对象执行的概率数据。

假设2 由于面向对象设计(Object Oriented Design,OOD)的软件使用有效性量化的框架,因此每个OOD指标都会影响某些质量因素,该框架如图1所示。根据所选自变量的值,即数据访问度量(Data Access Metrics,DAM)、功能抽象度量(Measure of Functional Abstraction,MFA)、直接类耦合度量(Direct Class Coupling,DCC)、方法内聚度量(Cohesion Among Method,CAM)、多态方法数量(Number of Polymorphic methods,NOP),进行线性组合计算[4]。

图1 面向对象设计的量化框架

I实例的计算公式为

I=[α0±(α1×Encapsulation)±

(α2×Inheritance)±(α3×Coupling)±

(α4×Cohesion)]

(1)

选择MFA,DCC,CAM来计算复杂度,使用SPSS数据分析软件对系数进行回归性分析。其中,模型系数如表1所示,得到复杂度的计算系数

表1 模型系数

Complexity=2.192-0.896×Inheritance-0.096×Coupling-0.078×Cohesion

(2)

假设3 在计算P值时,跟踪该对象在后续执行中产生故障的情况。当系统发生故障时,记录中间过程传递的所有K个对象,K个对象的I值的乘积为P值,即

(3)

如果未到达故障暴露的结点,则将P值设置为零。当分析计算分别获得对象的E值、I值和P值时,对象模块的可测试性即为三者的乘积。该方法注重分析软件系统的结构,对象的I值计算为非精确性数据,着重对类中的程序进行逻辑分析,充分运用了基础的PIE模型[4-5]。

2 应用随机图理论的软件可测试性计算模型

2.1 软件系统的随机图抽象

BRIAND L[1]提出将软件系统用图进行抽象表达,任何软件系统均可以抽象为结点的集合以及结点之间的若干类型边的集合。本文软件图中的结点表示对象,即为类、若干行代码或相应的文档。将结点之间的若干连接均抽象为边,如具有继承关系的两个类。依据以上理论,将面向对象的软件系统抽象为随机图[6-7],其中包含弱结点和强结点两类结点。软件系统中的故障经过弱结点进行传播、感染和扩散,其特征可以运用凯莱树(Cayley Tree)的渗透模型[8]进行表征。

假定消息能双向传递,即构造随机无向图G有N个结点和Q条边。有两种基本的概率结构来表示随机图,如文献[8]中的模型A。在该模型中,Q为一随机生成的变量,假设被连接的每对结点i和j的概率相等,其概率取值为p,并且这些概率之间彼此独立。若某图有N个结点,即存在N(N-1)条可能的边,则随机变量Q就以一个均值为〈Q〉的二项随机变量分布。均值的计算公式为

(4)

据此能以概率p和结点数目表示一个随机图,即G=G(Q,p)。

定理1从随机图的某结点i出发,其边数ri为结点i的次数,所有次数之和为2倍的边数,即

(5)

定理2若图的全部结点均具有相同的次数r,则此图被称为r次正则图。在模型A中,当N为最大值时,次数的平均值为

(6)

若N取某一较大值时,假定概率p为常量,则任何随机图G=G(Q,p)均趋向正则[7]。

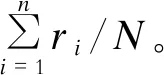
软件模型图是否缺乏正则和统一的本质特性,可以从以下3个方面进行分析。第一,确定软件系统的经验关联分析,并在概率的基础上对软件系统进行图形化抽象,但这方面还需要进一步的研究。第二,软件系统虽非正则,但若采用近似随机表达,则理论上为局部性正则。因此,大型软件系统可以分解为若干个连通子图,子图则可以被当作大型软件系统的子模块,若干连通子图为近似正则。第三,随机图理论对图的拓扑变化具有很强的鲁棒性,即改变链接或加强结点不会从根本上改变随机图的基本性质。因此,本文先将整个软件系统抽象成随机图,为软件故障传播建立量化规则做准备。

2.2 应用传播感染免疫理论的软件随机图模型

具有传染性的软件系统故障感染可以用随机图的方式来表达。参考PIE模型,若测试输入均匀进行,对象发生突变,并经过随机图中的边进行故障传播,则引入免疫的概念。

软件故障随机图中有弱结点和强结点两种互斥结点。弱结点受故障影响时易受感染,则表示故障隐蔽性强;强结点的可测试性较好,对故障传播有很强的免疫力,即表示故障较易暴露。在单元可测试性分析过程中或软件测试期间可依次对两种结点进行分辨。为了提高软件的质量,进而对弱结点单元进行改进,假设故障从弱结点开始,则传染操作在弱结点发生,程序在强结点失效,故障得以暴露。

某软件系统拥有N个结点,包括S个强结点和W个弱结点。设q=W/N,对于任意给定的结点,则其想要连通的结点为弱结点的概率约为q。对于任意给定的结点x和y,设故障从x传播到y的概率为s。q和s是反映不同类型软件系统特性的统计参数。

设q和s的值均较小且彼此独立,如上所述,大规模图一般为近似正则,即r次正则。若故障发生在强结点,则故障暴露率非常高,且故障将停止传播。但在弱结点发生故障时,则可能会导致相应的一系列故障,最后在途经强结点时被暴露出来。

用C记录故障链中包含的结点数。C的概率分布情况用F(x)表示,即

F(x)=p(C≤x)

(7)

式中:p——概率。

由于系统的次数为r,故有r个结点与故障状态的结点连通。这r个连通结点是弱结点的概率为q,连通弱结点能被传播故障的概率为s,则若干对象之间故障将会以概率qs传播,最终故障会引起系统失效。受到故障感染的所有弱结点个数为W项总和,各项分布均为F。

这里一个关键的简化是假设一个弱结点上的故障在没有循环的情况下通过树传播。下面是对这一假设有效性的简短证明。

根据随机图的理论,给出一个临界点,此临界点以下,图大概率是以树的形式呈现。若某一图中有N个结点,则连通分量中出现环的概率为1/N。在一个规模较大的随机图中,结点之间能连通的概率小于1/N时,则图大概率是以树的形式呈现。在本文中,两个结点通过故障传播连接的概率为pqs,所以,若这个假设是合理的,即仅需符合pqs≤1/N。故障经由树进行传播,则该过程可表达为在连通概率为t=qs、分支数为r的凯莱树上传播。事实上,在软件运行时,故障可以通过概率qs传播到r个相邻结点之一,并且不生成环,而故障传播的每一步,都会在r个非交叉的路径中选择。凯莱树是固定步长分支的图形拓扑结构,因此上述连通树中包括所有原始结点,结点数C为随机值,其平均值为

(8)

2.3 基于对象粒度的软件可测试性计算模型

基于对象粒度构建改进的PIE计算模型。若I为弱结点的变异故障率,E为其执行概率,则根据式(3),其P值的平均概率表示为

(9)

在故障传播的路径中,第i个对象模块的变异故障率为Ii,其可测试性计算式为

(10)

上述计算模型的相对值可以评价软件可测试性的差异程度,但绝对值的意义不大。

3 结 语

软件可测试性是软件有效测试难度的一个指标。如果可以用特定的值来量化可测试性,则可以更方便地评估软件测试的难度,也可以更准确地衡量测试工作量。本文结合随机图理论和扩展PIE模型来分析面向对象软件的可测试性,获得的数据可以反映对象的可测试性,提供了最可靠的数值依据来判断模块是否需要重构,以实现对软件开发过程的辅助决策。