兼顾投资成本和年发电量的河流小水电厂多目标优化

□王伟伟

水利发电是清洁能源、绿色能源，同时，水电站具有可靠性较高、发电效率较高以及维护成本低的特点。现以NSGAII为优化算法，以年发电量和投资成本为目标函数，以发电机组数量（n）和额定水轮机流量（QT）为目标函数，提出水电站优化规模的多目标优化方法作为决策变量，研究决策变量对目标函数的影响，确定年发电量与水电站投资成本之间的最佳权衡。

1.数据与方法

1.1 数据

案例研究的重点是位于某径流式水电站的水力资源。图1显示了平均日水流量。根据这些平均日水流量，我们建立了流量-频率曲线，见图2，用于调查可用流量，从而选择合适的涡轮机。我们将选择适用于水电站的水轮机，同时使用净水头(Hnet=119.5m)和四种特征流量，分别为第1个四分位数（Q75%=0.06275m3/s），中位数（Q50%=0.15m3/s），第3个四分位数（Q25%=0.485m3/s），以及年平均流量（Qmean=0.491m3/s）。

1.2 水轮机

任何水电站水轮机类型的选择取决于现场特征，如净水头和河流流速。图3显示了水轮机根据净水头和流量进行的分类，可用于为水电站选择最合适的水轮机类型。考虑到上述的流量参数净水头(Hnet=119.5m)，和4种特征流量Q75%，Q50%，Q25%，以及 年 平均流量Qmean，显然最近的是冲击式水轮机。因此，本研究考虑使用冲击式水轮机。

1.3 小型水电站水轮机年发电量模型

将水势能转化为机械能，最终由发电机转化为电能。水电站年发电量E（kW·h）计算公式如（1）所示：

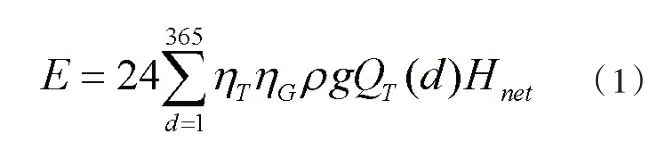
式中：

ρ—表示水的密度（kg/m3）；

g—重力加速度（m/s2）；

Hnet—净水头（m）；

QT（d）—日平均流量；

ηT和ηG—涡轮机和发电机的效率，发电机效率约为90%。

用于表示涡轮效率变化经验表达式（2）：

图1 平均日水流量

图2 流量—频率曲线

图3 涡轮机选择列线图

图4 水电站年发电投资成本优化结果

式中：

QTr和ηTr—标称涡轮流量和效率；a、b和c为系数。

1.4 小型水电站投资成本模型

基于机组数量的低水头坝趾小水电站造价模型分析估算小型水电站的投资成本。选择此模型是因为它们不仅取决于输出功率（kW）和净水头（m），还取决于发电机组数量（n），这是研究中的一个决策变量。优化问题公式，目标是最大化年发电量公式（3），同时最小化n台水电站的投资成本公式（4）。我们将使用NSGAII找到这两个目标函数之间的权衡。

表1 与典型最优解对应的决策变量

表2 获得各类帕累托最优解的参数

图5 水电站投资成本决策变量敏感性分析

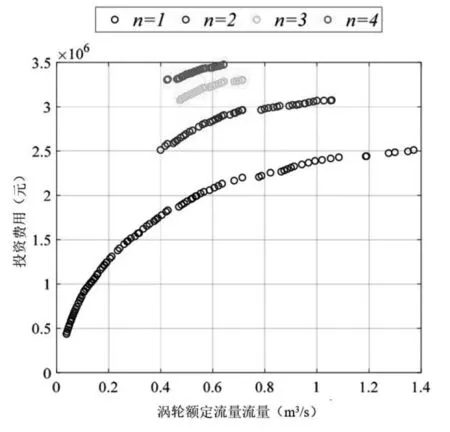
图6 水电站年发电量决策变量敏感性分析

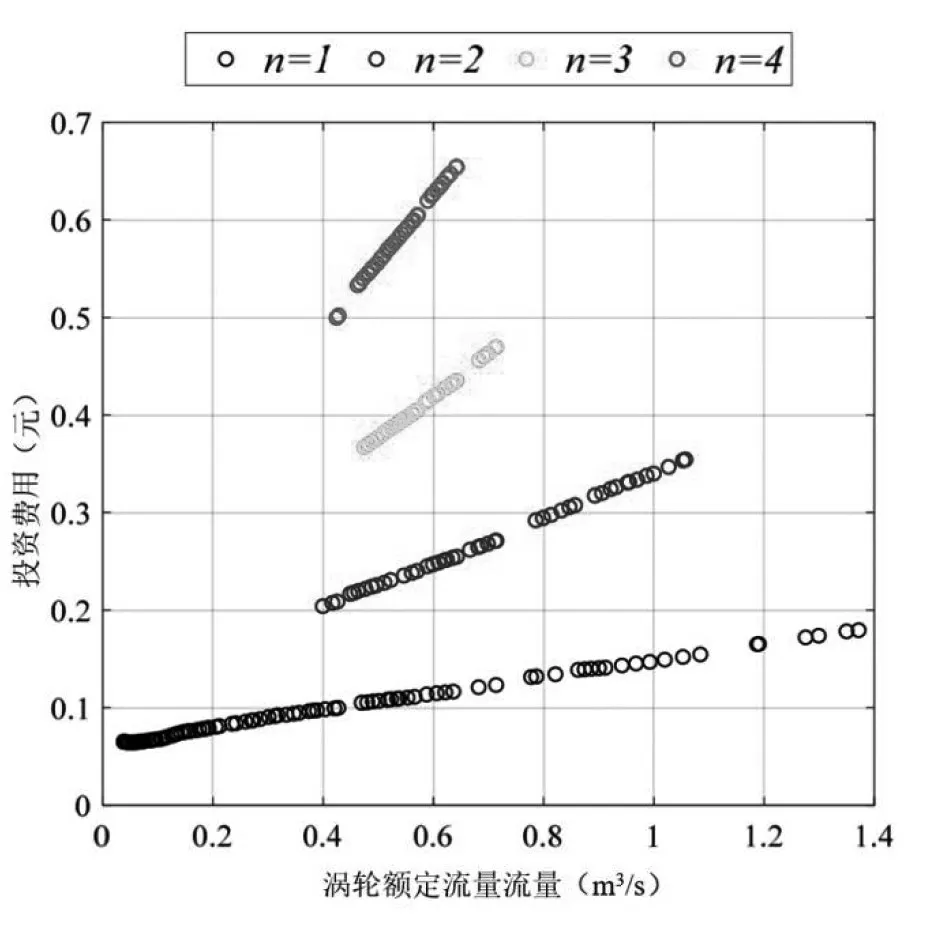
图7 水电站每kW·h投资决策变量敏感性分析

式中：

Cinv—年开发的n台水电站的投资成本；

P—n台发电机组提供的功率输出。

2.结果

2.1 帕累托最优值

图4所示的帕累托最优值给出了经过100代计算后得出的200个最优解。每个解决方案都包含一组用于水电站规模确定的最佳参数。这些解决方案构成了年度发电量和水电站投资成本之间的最佳权衡。我们可以注意到，随着年发电量的增加，投资成本上升。因此，最大化年发电量与最小化投资成本是矛盾的。在图4中，解决方案A提供了最低的总年发电量和最低的投资成本。同样，解决方案C提供的总年发电量最高，正如预期的那样，也是最昂贵的。中间解决方案B提供中间投资成本和年发电量。对应于解A、B和C的最优决策变量如表1所示。我们可以注意到，对于这些解，决策变量随着两个目标函数的增加而增加。

2.2 决策变量对目标函数的敏感性分析

图5~7分别说明发电机组数量和标称涡轮机流量对投资成本、年发电量和每千瓦时投资成本的敏感性。根据发电机组数量（n），帕累托最优解分为4类：黑色（n=1）、蓝色（n=2）、绿色（n=3）和红色（n=4）。当年发电量增加时，投资成本（图5）和每千瓦时投资成本（图7）几乎随着标称涡轮机流量的增加而线性增加，随着标称涡轮流量的增加对数增加，见图6。

在表2中，最佳解决方案的数量、标称涡轮流量、投资成本、年发电量和每千瓦时投资成本的变化范围显示在发电机组数量之后（等于1、2、3或4）。

3.结论

研究提出一种同时考虑年发电量和投资成本的水电站优化规模的多目标优化方法。机组数量和额定涡轮流量构成决策变量，NSGAII被用作优化算法。利用总水头、流量的第一个四分位数、中位数、第三个四分位数及其平均值，对水电站的环境特征进行调查。调查结果证实，冲击式水轮机是该水电站最合适的水轮机类型，多目标优化的最优解已经收敛到帕累托最优解，这些解决方案构成了年度发电量和水电站投资成本之间的最佳权衡。每个解决方案都包含一组用于水电站规模确定的最佳参数，随着年发电量的增加投资成本上升，最大化年发电量与最小化投资成本是矛盾的，决策变量对两个目标函数的敏感性分析表明，决策变量随两个目标函数的增加而增加，帕累托最优解已根据发电机组的数量进行分组，投资成本和每kW·h投资成本几乎随汽轮机标称流量的增加而线性增加，而年发电量则随汽轮机标称流量的增加而对数增加。