砖石古塔静力分析方法探讨
张旭强
(山西工程科技职业大学,山西 晋中 030619)
在我国,砖石古塔形态多变、风格各异、分布非常广泛。这些修建于不同年代的建筑对于研究我国古代的建筑工艺、建筑历史、建筑文化具有非凡的意义,而且对于研究我国古代的政治、经济、宗教、艺术等都具有重要的价值。
由于砖石古塔的建造高度比较高,长细比大,同时受到建筑设计、工艺水平等内在因素和人工活动、不可抗力等外部条件的影响,许多保存至今的古塔都产生了不同程度的倾斜,“十塔九偏”是公认的现实。为了对砖石古塔进行有效的保护和修缮,探讨砖石古塔,特别是位于湿陷性黄土地区的砖石古塔纠偏及加固技术显得尤为急迫。
1 有限元模型的理论基础
有限元法通过将连续体离散化为各个互不重叠的单元,单元和单元之间有联结节点,通过联结节点组成一个单元集合。假设在平面问题中,所有的节点都为铰结点,所有作用在单元上的不同荷载,例如集中荷载、体积荷载和表面荷载等,都要作为等效荷载按虚功原理移置到节点上。最后得到的计算结果为相应的节点处的一系列离散型数值,利用这些离散型数值推算其他未确定的数值[1]。
1.1 设定形函数和位移函数
根据单元节点联结情况设定位移模式,设定位移函数,然后用节点位移表示位移函数中的待定系数,从而得到位移函数如下:
{f}=[N]{δ}e
(1)
上式中[N]为形函数矩阵,由各形函数组成。
1.2 应力矩阵和应变矩阵
根据几何方程,再利用物理方程,将单元内的应力和形变用节点位移表示如下:
{ε}=[B]{δ}e
(2)
{σ}=[S]{δ}e
(3)
[S]=[D][B],其中矩阵[D]是应力应变之间本构关系的反映,[B]为形变转换矩阵,[S]为应力转换矩阵。
1.3 单元刚度矩阵
解决几何非线性问题,考虑虚位移,形变转换矩阵[B]为单元节点位移列阵{δ}e的函数,应力和应变的关系用单元刚度矩阵来表示,采用增量形式可以表达如下:
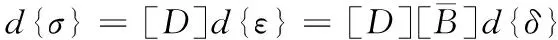
(4)

2 弹性和弹塑性本构关系
应用有限元法分析土体的应力和变形问题时,需要确定土体的本构关系,尤其涉及土体非均质性、非线性和复杂边界等问题。土的力学本构关系反映了土体变形的特性,是建立本构模型[2]的根据,也是检验本构模型理论的客观标准。
研究土体在受荷载作用时的变形特性,形成了弹性理论和弹塑性理论,和本构关系结合建立为模型,一直以来不断推动土的本构理论的发展。现阶段,土体应力-应变-强度(时间)关系的本构模型相对和实际接近,并且能有效地将变形特性和应力分析相互结合,提高计算精度,解决复杂问题。
2.1 土的非线性弹性模型
实际非线性在工程中用来体现土的应力应变关系比较贴切,也反映了应力和应变的复杂关系。依据广义虎克定律,非线性弹性模型建立刚度矩阵[D]。由于属于非线性关系,刚度矩阵[D]中的弹性常数v、E被当作变量,而且是会随应力状态而改变的。
理论上,非线性弹性模型有3种类型:Cauchy弹性模型、Hyperelastic超弹性模型和Hypoelastic次弹性模型。Duncan-Chang双曲线模型在非线性模型中是最有代表性的模型。1970年Duncan和Chang提出了双曲线模型,其依据土体常规三轴试验,只在一个方向施加应力增量,从而得到的土体应力-应变曲线,见如下双曲线方程来表示[3,4]:
(5)
式中:a,b—双曲线函数参数;σ1—轴向应力;(σ1-σ3)—主应力差。
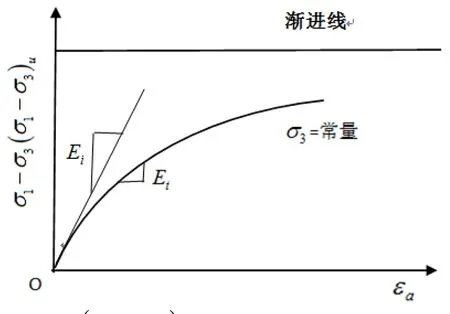
图1 (σ1-σ3)-εa关系曲线
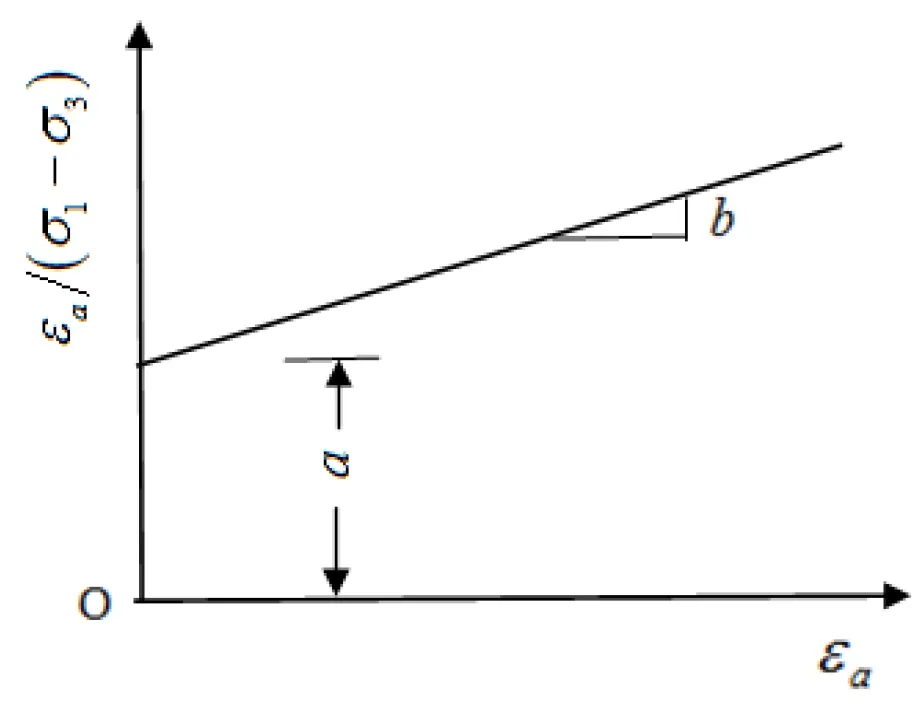
图2 εa/(σ1-σ3)-εa关系曲线
最终推导得出Duncan-Chang模型(E-B模型)的切线模量方程为:
(6)
表达式中:K—试验常数;Et—切线模量;Rf—破坏比;Pa—大气压力器。
卸荷、重复加荷,此时弹性模量值的表述如下:
Eur=KurPa(σ3/Pa)n
(7)
式中:Kur—试验常数,一般情况下Kur=(1.2~3.0)K。
式(6)(7)是推导来的切线弹性模量方程,实际上也可以看出来是常规三轴试验应力应变曲线的切线斜率的反映,强度随应力水平的变化关系或随固结压力的变化关系都可以在上述公式中有所体现。至于Eur的应用,实际上是一个屈服准则的使用标准,不过略显粗略。1980年Duncan根据不同土类试验分析把E-μ模型修正为E-B模型,并且提出了体积模量B的公式,如下:
B=KbPa(σ3/Pa)m
(8)
式中:Kb—体积模量系数;m—取值为0~1.0,无量纲。
上面提到的Duncan-Chang双曲线模型能反映土体的主要变形特性,而切线的弹性常数通常是用试验曲线而定。土的非线性模型利用加载模量和卸载模量来部分反映,此处采用的参数物理意义也是比较明确的。尽管如此,Duncan-Chang双曲线模型仍有许多方面的问题,例如,没有反映土体变形的规律,也没有反映土的剪胀性情况,更不能反映出主应力对模量的影响程度,不能反映平均正应力的变化对剪应变的影响,也就是说不反映压缩与剪切的影响,也不反映各向异性。
2.2 土的弹塑性模型
理论上,如果全部变形都是弹性的,这一假定反映了弹性非线性模型设立的初衷,如果要反映非线性,则相应地改变弹性常数;而对于弹塑性模型,则要把变形分成两部分:弹性变形和塑性变形。弹性变形部分用虎克定律来计算,塑性变形部分则用塑性理论来解决问题。
不同的弹塑性模型,假定也不同,主要体现在假定的形式上。但是一般要从几个方面去假定,如破坏的准则或屈服准则、流动法则、硬化规律等。在破坏准则方面有Tresca准则、Mises准则等,其中一些受到广泛应用,因为要判断破坏与否,而破坏又取决于土体应力状态。当土的应力状态达到一定的屈服标准以后才能硬化,这时候的屈服就形成了塑性变形,用塑性变形来衡量硬化发生的程度,引入函数,结合起来反映硬化规律。屈服函数和硬化规律仅仅是给定了判断屈服的标准和屈服后如何发展变化,但是没有衡量变化的比例,这就需要确定应变增量或变化的方向问题,而流动规则是用于确定塑性应变增量方向的假定的。弹塑性理论可以反映土体的各种变形特性,但是并非全面,也有其局限性,也依赖于选定的模型。
3 建立计算模型
砖石古塔静力分析的几何模型由塔体和地基两部分组成,根据上部结构的原始尺寸建立模型,然后调整倾斜值,形成实体模型。根据地质勘察资料并结合地基土在深度方向上的分层特点建立地基模型,深度方向上地基模型与勘察一致,土层宽度方向上与古塔底面横截面相关,取横截面换算半径的10倍。
图3中,实体建模的方法采用自底向上。从基本的点、线、面构造大象寺塔实体,使用程序运算组合数据集,组建实体模型。

图3 实体模型
3.1 选择单元类型
砖石古塔静力分析,要涉及塔体与相关地基,因而要选择空间实体单元。目前常用的结构空间单元比较多,例如SOLID65、SOLID95、SOLID147、SOLID185、SOLID186等。这些可选择的单元类型的自由度和节点各不相同,本例选择SOLID95单元作为塔体和地基的实体单元。
SOLID95单元包括20个节点,如图5所示,各节点沿x、y、z有3个自由度,具有塑性、蠕变、应力刚度、大变形和大应变能力等特性。

图5 SOLID95
3.2 定义材料特性
本例中上部塔体运用线弹性模型,模型中参数有弹性模量E和泊松比μ。参数数值的确定参考同时代当地已有数据,根据陕西文物保护中心提供的数据显示,西安市长安区大雁塔材性参数取值如下:砌筑砖的标号MU15,砂浆等级为M0.4,参照砌体规范中砌体的弹性模量[5]取值E=700f(其中,f=1.12MPa,f为砌体的抗压强度设计值),得到弹性模量E=784MPa,泊松比取值0.15,密度取值1 900kg/m3。
砖石古塔的地基土,模型参数的确定没有已有经验数据参照,根据土的变形模量E0与土体物理性指标的关系,经过整理统计土的物理性质试验资料,得出相对接近的模量参数,即通过计算得到的变形模量E0[6]数值:
变形模量与物理性指标之间的关系如下:
(9)
(10)
当缺乏试验资料时,可按下式经验方法确定μ0,即:
μ0=(1-sinφ′)/(2-sinφ′)
(11)
以上是土体本构模型中弹性部分的参数确定过程,土的塑性本构模型还未确定。由于土的受拉屈服强度[7]远小于受压屈服强度,本例可采用Drucker-Prager屈服准则来计算。
采用DP模型,地基条件为黄土,基本参数为c、φ、ω、ρd等,根据室内土工试验数据,不同干密度ρd时含水量和与c、φ值的试验对比如表1所示。

表1 不同干密度时含水量与黄土抗剪强度的试验对比
4 算例分析
大象寺塔位于陕西省合阳平政乡安阳村东北,又名“大云禅院”(见图4),此塔建于唐代,砖塔为叠涩密檐式,呈方形。塔体共有13层,其中第一层内有券洞,行可入内洞,上层为封死实心砖,塔体顶层已损坏部分,不可修复,底层南面砖体损坏。塔高25.88m,下有长宽各4.8m的方形基座。塔体明显向东北方向倾斜:北偏东20°56′2″,垂直方向倾角3°51′28.8″,中心偏差1.595m。塔体的西南角比西北角高出26cm,东南角比东北角高出23cm。

图4 大象寺塔
本例中地基模型为层状,设置两层地基土,依据前期地质勘察获得资料数据,结合室内土工试验测定的土性指标参数,每层设置厚度与实际的土层厚度保持一致。①黄土状土为地面下第一层地基土:厚度1.69m~2.12m,黄褐色,大孔隙发育,含氧化铁、丝状碳酸钙,土质较为均匀,属压缩性黄土,中等具湿陷性,稍湿、硬塑~可塑,稍密。②地面下第二层为黄土状土:厚度3.68m~4.48m,含氧化铁呈褐黄色,蜗牛壳状,为大孔隙发育,粉土占比明显,土质较为均匀,属高压缩性黄土,稍湿,硬塑~可塑,密实。如图6网格化为有限元模型,然后对模型加载并计算得到结果。

图6 有限元模型
从求解结果看,节点位移、约束反力及节点力都不同程度反映目前塔体受力情况,尤其变化明显的部位是在塔体与塔基接触处,真实反映了塔体和塔基受力情况,应力分布规律[8]体现着与应变相对应关系。在图7中,X方向为上最大位移发生在抬升的塔体下部,数值为26.44mm,并向外扩散,图8应力则主要集中在塔体和塔基接触部位,尤其在倾斜明显的一侧。分析原因,古塔为砖石结构,塔体自重大而强度又低,一旦发生倾斜,往往会造成倾斜明显的一侧地基应力相对集中,而相对集中的应力又会进一步加速建筑物的倾斜程度。同时砖材料组成的结构墙体在不同的水平截面上的压应变是不同的,收缩量也不同,因而压应变的分布也不是均布的,多个截面的差异变形累积,造成结构初始偏心。利用程序对各个分析结果进行整理,X方向结构应力最大的点19节点为88 291Pa,应变最大的点17节点为-0.16622E-03。在古塔纠偏时参照位移、应力、应变列表对塔体结构中相应的薄弱部分进行加固。

图7 X方向位移分布云图

图8 X方向应力分布云图
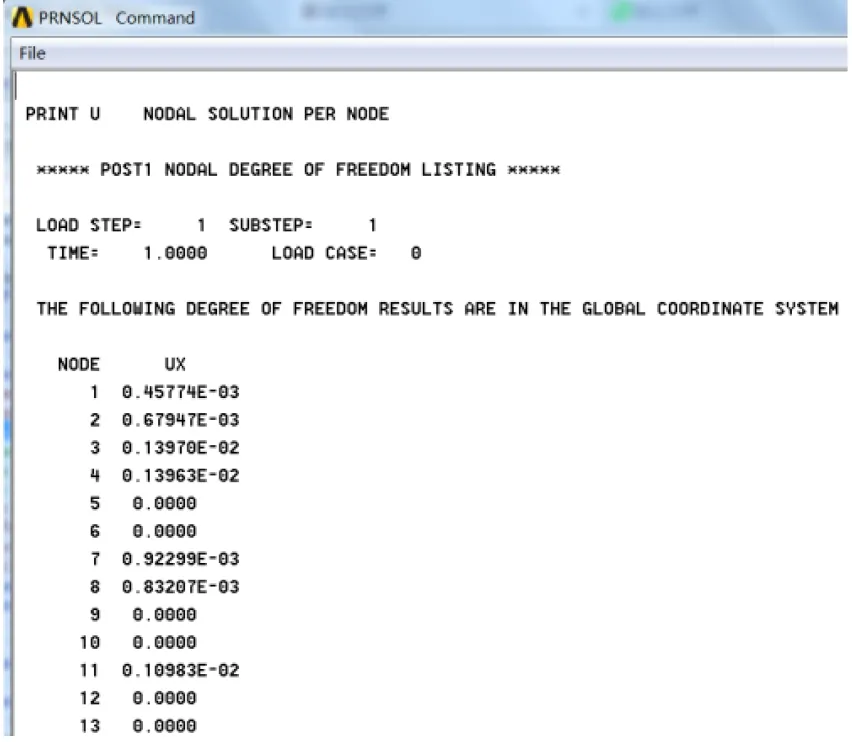
图9 X方向节点位移列表

图10 节点应力列表
5 结论
①利用有限单元法进行数值分析,涉及土的本构模型的选择,典型的土的本构模型有非线性弹性模型和弹塑性模型两种,分析黄土的变形特性,相比非线性弹性,地基土体弹塑性模型比较合适本例数值计算。②有限元模拟分析,在对砖石古塔纠偏时,地基模型选择有限地基模型。有限地基模型与古塔底面横截面相关,取横截面换算半径的10倍。③运用有限元静力分析古塔的倾斜原因,探讨塔体和地基的位移、应力、应变状态,为选择合理的纠偏加固方法、制定纠偏加固技术方案提供依据。

