无监督空谱近邻超图嵌入高光谱图像特征提取

陶 洋，翁 善，林飞鹏，杨 雯

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

近年，高光谱成像技术已被广泛应用于诸多领域[1,2]。高光谱具有波段数众多、波段相关性强等特点，此类特点极易造成“维数灾难”问题[3-5]。由于缺乏足够的先验知识，导致数据标注困难的问题。因此，相关学者提出无监督的高光谱特征提取方法。基于流形学习[6,7]的无监督特征提取方法可以发现高维数据中的低维流形结构，能有效表征高光谱数据的本征结构。流形学习方法可以统一在图嵌入[7]框架下，通过顶点和边来构建图，利用边表示两个数据点之间的相似性。除了基于几何特性的图嵌入方法，Ly等[8]和Li等[9]还引入了稀疏表示方法揭示数据内在关联特性。然而，稀疏表示之所以有效是因为协同机制，故而放弃算法复杂度高的l1范数，转而利用简单高效的l2范数最小化问题[10,11]。这些无监督图嵌入特征提取方法都属于直接图嵌入方法，即只考虑数据间的一元关系，但是高维数据往往存在多元复杂关系[12]。Yuan等[13]利用光谱信息构建超图，表征数据之间的多元关系。但是，上述图嵌入特征提取算法忽略了高光谱图像的空间信息，研究已表明空谱联合可提高特征提取性能[14,15]。本文中，提出无监督空谱近邻超图嵌入(spatial-spectral neighbor hypergraph embedding，SSNHGE)特征提取算法，以无监督的方式，发掘高光谱图像的空谱近邻关系，并且通过引入超图模型去表征高维数据的多元复杂关系，提取有效的鉴别特征，提高地物分类精度。

1 相关方法

超图与普通图的主要区别是边的顶点个数不同，普通图的边仅有两个顶点，然而超图的边可以有多个顶点。超图模型可以表示为G={V,E,W}， 其定义请详见参考文献[13]。

根据定义，不同于普通图一条边包含两个顶点，只能揭示数据两两之间的邻近关系。超图的边可以包含任意多个顶点，所以比普通图保留更多的信息。因此，超图适用于表示数据复杂的多元关系。例如，图1(a)为普通图，图1中有7个顶点，7条边，每条边仅能表示两个顶点的关系。图1(b)为超图，有7个顶点，3条超边，每条边由某个点与其近邻点组成，其对应的超图关联矩阵如图1(c)所示，与普通图对比，一条超边里面的点被分解成多对链接关系，易导致在构造图的过程中造成有价值的信息的丢失。由此可见，普通图是无法很好地表征高维数据结构。

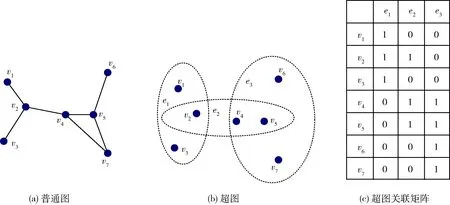
图1 超图与普通图对比

2 本文方法

SSNHGE算法的总体流程如图2所示，先充分利用无标签样本的空间信息与光谱信息建立无监督近邻关系，继而构建无监督空谱近邻超图模型，然后利用超图嵌入方法获得低维投影矩阵，继而获得高光谱数据的低维嵌入特征，最后采用分类器对其分类，获得地物分类结果。

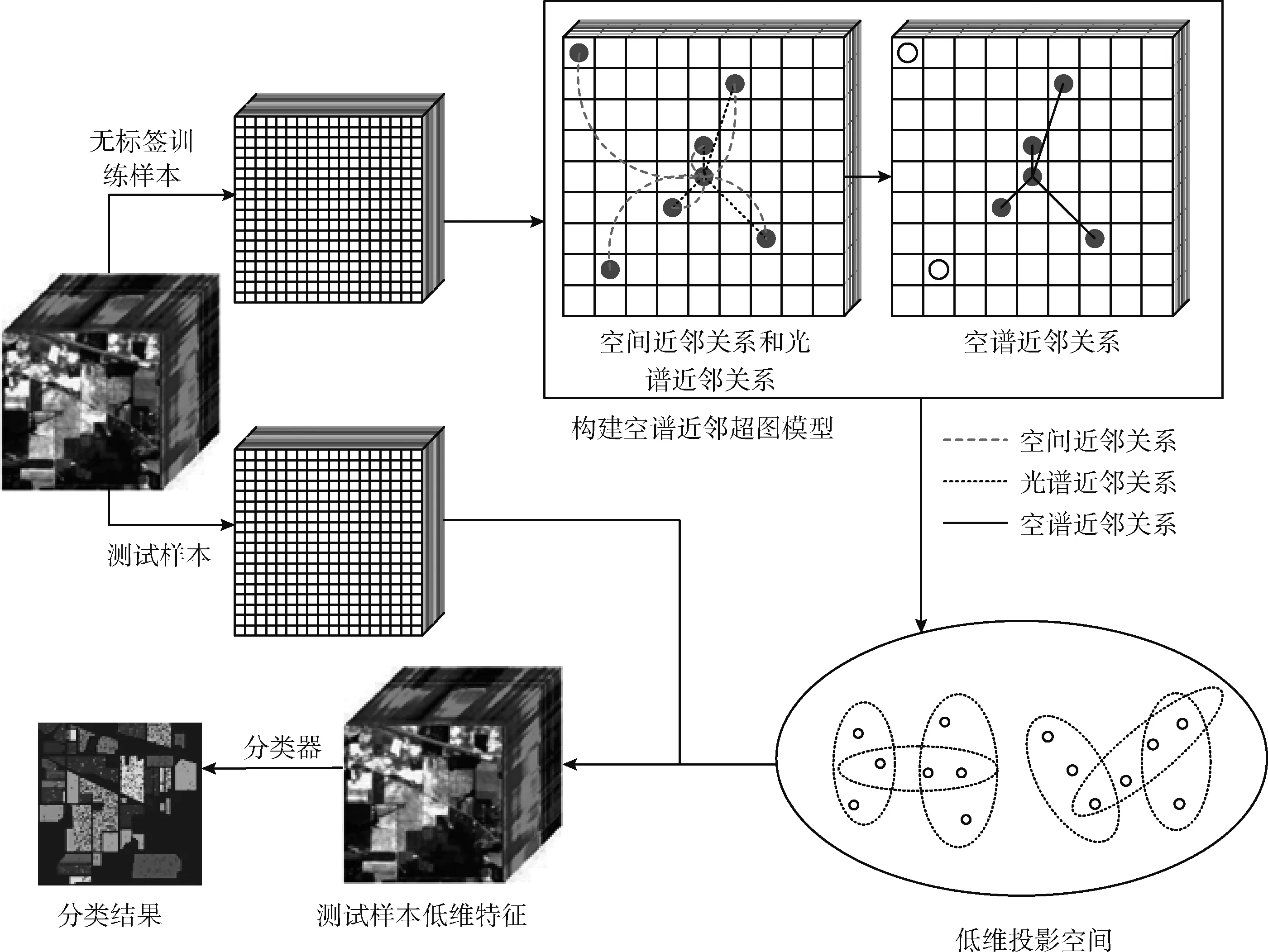
图2 SSNHGE算法流程

本文所提算法与其它同类算法相比，具有两方面创新点。其一，传统方法以局部矩形窗口构建空谱近邻关系，由于训练样本少，易出现局部窗口内未能找到近邻点导致构图失败，以及在无监督的情况下近邻点的选择易出现不合适的问题。为解决此类问题，利用全局空间结构信息寻找空间近邻点集合，再从中选择出光谱特征相似度最接近的近邻点集合，由此构建有效的空谱近邻关系；其二，有效地利用空谱信息构建超图模型，以表征高维数据多元复杂关系，解决直接图嵌入方法在构图过程中没有做到信息的有效利用，以及构图时容易丢失有价值的信息的问题。

2.1 无监督空谱近邻超图模型的构建

针对普通图仅能表征数据之间的二元关系造成构图过程中有效信息丢失的问题，引入超图模型表征高维数据之间的多元复杂结构；针对带标签样本获取困难和传统的图嵌入方法仅采用光谱特征相似度对高光谱图像中每个像元进行独立处理，难以充分反映其本身的相似性的问题，可通过有效地挖掘高光谱图像像元之间的空间相关性，再利用空间相关性提取高光谱图像的空间信息，并协同光谱信息进行有效的近邻的选取，克服在构造无监督超图过程中“同谱异物”或“异物同谱”等问题所带来的不良影响。提出无监督空谱近邻超图模型，根据高光谱数据每个像元的光谱信息和空间信息来构建超图。首先，给定高光谱图像的无标签数据集V=[v1,v2,…,vN]∈RD×N， 其中，D和N是高光谱数据集的光谱维数和无标签像元数。每个像元携带自身的空间坐标信息，可定义为vi(pi,qi)， 其中，pi,qi代表像元vi的空间坐标信息。如此，构建以vi为中心的空间近邻集合，根据vi与其它像元的曼哈顿距离构建其空间近邻集合，可表示为

(1)

(2)

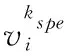
(3)

由超边矩阵E可构建关键矩阵H，其关联矩阵可定义为

(4)

(5)

顶点vi的度与超边ei的度可表示为

(6)

(7)

根据式(5)、式(6)、式(7)可构建其超边权重矩阵、顶点的度矩阵和超边的度矩阵

(8)

(9)

(10)

2.2 超图嵌入

超图嵌入模型的目的是在特征学习的过程中，尽可能地保留高光谱数据局部空谱近邻结构的同时，有效地在嵌入空间中提取出低维鉴别特征。通过式(4)、式(8)、式(9)和式(10)共同构建其目标函数，表示为

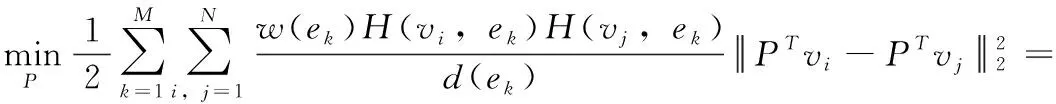
(11)

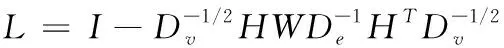
(12)

其中，正则项VVT用于保持样本的多样性。对式(12)采用拉格朗日乘子法求解可得

VLVTP=λVVTP

(13)

求解式(13)的广义特征值和特征向量，再对特征值进行升序排序，取排序后的前d个特征值所对应的特征向量重新构造成投影矩阵P∈RD×d， 低维嵌入特征可表示为Y=PTV∈Rd×N。 最后，SSNHGE算法的具体流程见表1。

表1 SSNHGE算法流程

3 实验验证与结果分析

采用公开的Indian Pines和Salinas高光谱图像数据集，通过与同类型算法进行对比以验证本文算法的有效性。同类型的特征提取算法含局部保持投影(locality preserving projection，LPP)[6]、近邻保持投影(neighborhood prese-rving embedding，NPE)[7]、基于稀疏表示的稀疏保持图嵌入(sparsity preserving graph embedding，SPGE)[8]特征提取算法、稀疏低秩保持图嵌入(sparsity and low-rankness preserving graph embedding，SLPGE)[9]、协同表示图嵌入(collaboration preserving graph embedding，CPGE)[10]以及协同竞争保持图嵌入(collaboration-competition preserving graph embedding，CCPGE)[11]算法。为公平起见，实验中利用各特征提取算法获得到各低维嵌入特征后，统一采用支持向量机(support vector machines，SVM)分类器对各算法特征提取后的高光谱数据进行性能测试，然后利用总体分类精度(overall accuracy，OA)、平均分类精度(average accuracy，AA)和Kappa系数(kappa coefficient，KA)3种评价指标去评估各算法的性能。为提高实验可靠性，每次实验从高光谱数据集中以随机的方式抽取训练样本，其余作为测试样本，每组实验重复10次，以平均值作为最终实验结果。

3.1 数据集介绍

(1)Indian Pines数据集为美国宇航局在1992年利用AVIRIS传感器拍摄位于美国印第安纳西北部地区，其范围为100 km2，其尺寸为145×145像素，共220个波段，0.4 μm～2.45 μm的光谱范围，空间分辨率为20 m，剔除受水气(噪声)影响的波段后，剩余200个波段可用于实验。该数据集含16类地物，如苜蓿(Alfalfa)、玉米(Corn)、小麦(Crop)等。该数据常用于农业研究领域，但是，其中Corn，Soybean和Crop这3类地物光谱曲线相近、相似度小且类间光谱重叠大，此类特点使得分类难度大大提升。其假彩色图、真实地物图、类别标记图及样本信息如图3所示，表2显示了用于训练和测试的样本数量。

图3 Indian Pines高光谱图像

(2)Salinas是加利福尼亚州萨利纳斯山谷区域高光谱数据。该数据集的空间尺寸为512×217像素，空间分辨率3.7 m，原始波段共224个，剔除受噪声影响的波段后，剩余204个波段可用于研究实验。该数据集含16类地物类别。图4展示的是Salinas数据集的假彩色合成图、样本信息和类别标记图。表3显示了用于训练和测试的样本数量。

3.2 参数设置

在实验中需要分析两个参数，空间近邻个数kspa和光谱近邻个数kspe， 本文测试了kspa和kspe参数在不同设置下对总体分类精度影响的实验，其中kspe必须小于kspa参数，若大于其值，kspe将失去意义。kspa参数设置为 {8,10,12,14,16,18,20,22,24,26}，kspe参数设置为 {4,6,8,10,12,14,16,18,20,22}。 图5显示了SSNHGE算法在Indian Pines和Salinas数据集上，kspe和kspa参数的变化对总体分类精度的影响。

从图5可以看出选择合适的参数对其分类精度有较大的影响，首先分析空间近邻个数对总体分类精度的影响，随kspa增大其分类效果呈现先增大后减少，这说明空间近邻

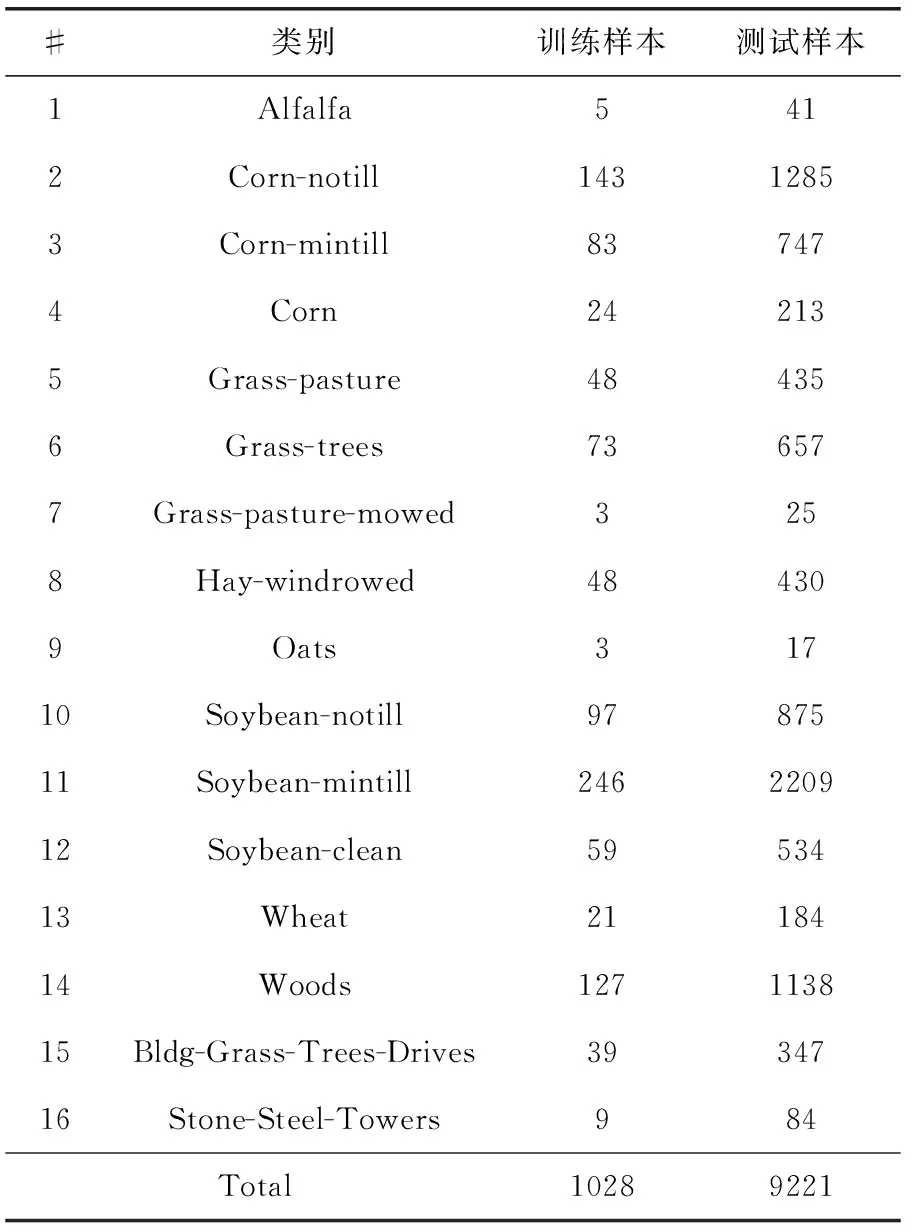
表2 Indian Pines数据集的训练及测试样本数量

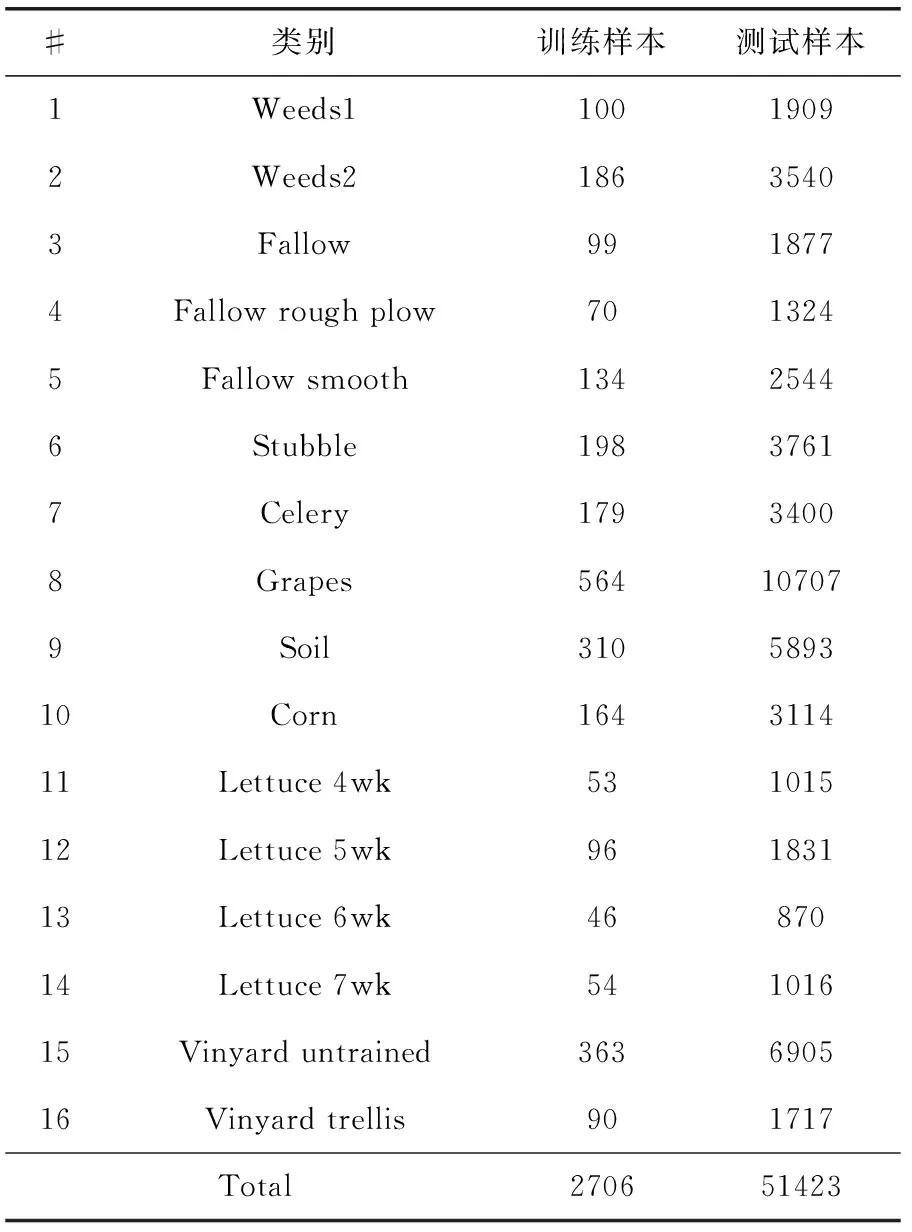
表3 Salinas数据集的训练及测试样本数量

图4 Salinas高光谱图像

图5 kspa和kspe参数对总体分类精度的影响

点过多，会导致本文算法不能有效表征同类数据间的本征结构。其原因是，当空间距离越大，像元的相似度也就越低，选取异类像元作为近邻点的可能性也就越大，当近邻结构图中异类点越多，同类数据间的本征结构表示效果越差。然后分析光谱近邻个数对总体分类精度的影响，随着kspe增大，其分类效果呈下降趋势，这说明光谱特征近邻点多会影响本文算法对数据的表征性能。其原因是，同样的光谱距离参数设置越大，引入噪点的几率越高，继而破坏鉴别特征提取性能，导致分类精度下降，故而选择合适的光谱距离和空间距离至关重要。所以，根据图5中的实验结果选出最优参数，在Indian Pines数据集上，kspa为20，kspe为4时其总体分类效果最佳；在Salinas数据集上，kspa为18，kspe为4时其总体分类效果最佳。

3.3 实验结果对比

高光谱数据的分类性能会受特征提取算法维数的影响。图6显示了LPP、NPE、CPGE、SPGE、SLPGE、CCPGE和SSNHGE特征提取算法在不同的特征提取维数d下的总体分类情况。从图6可知，无论是哪个数据集，各特征提取算法在特征提取维数d增加的情况下总体分类呈向上的趋势，且当提取特征的维数达到某个值后，各类算法的总体分类精度逐渐趋于稳定。例如，在Indian Pines数据集中特征提取维数d达到20后，各算法的总体分类精度趋于平缓；在Salinas数据集中特征提取维数d达到10后，各算法的分类精度趋于平缓。在图6中，很容易看出SSNHGE算法的总体分类精度在两个数据集上分类精度明显优于其它算法，尤其在Indian Pines数据集上，SSNHGE算法分类精度明显高于其它算法。可以验证，本文所提出的算法能够提取出有效的鉴别特征。

表4、表5所显示的是各类算法在两个高光谱数据集上的分类结果，含各特征提取算法对每一种地物分类精度、平均地物分类精度、总体地物分类精度以及Kappa系数，粗体数字为最优分类评价指标。图7展示的是Indian Pines数据集经过所提算法与同类算法特征提取后的分类结果图；各类算法在Salinas数据集上特征提取后的分类结果，如图8所示。

图6 维数d对总体分类的影响

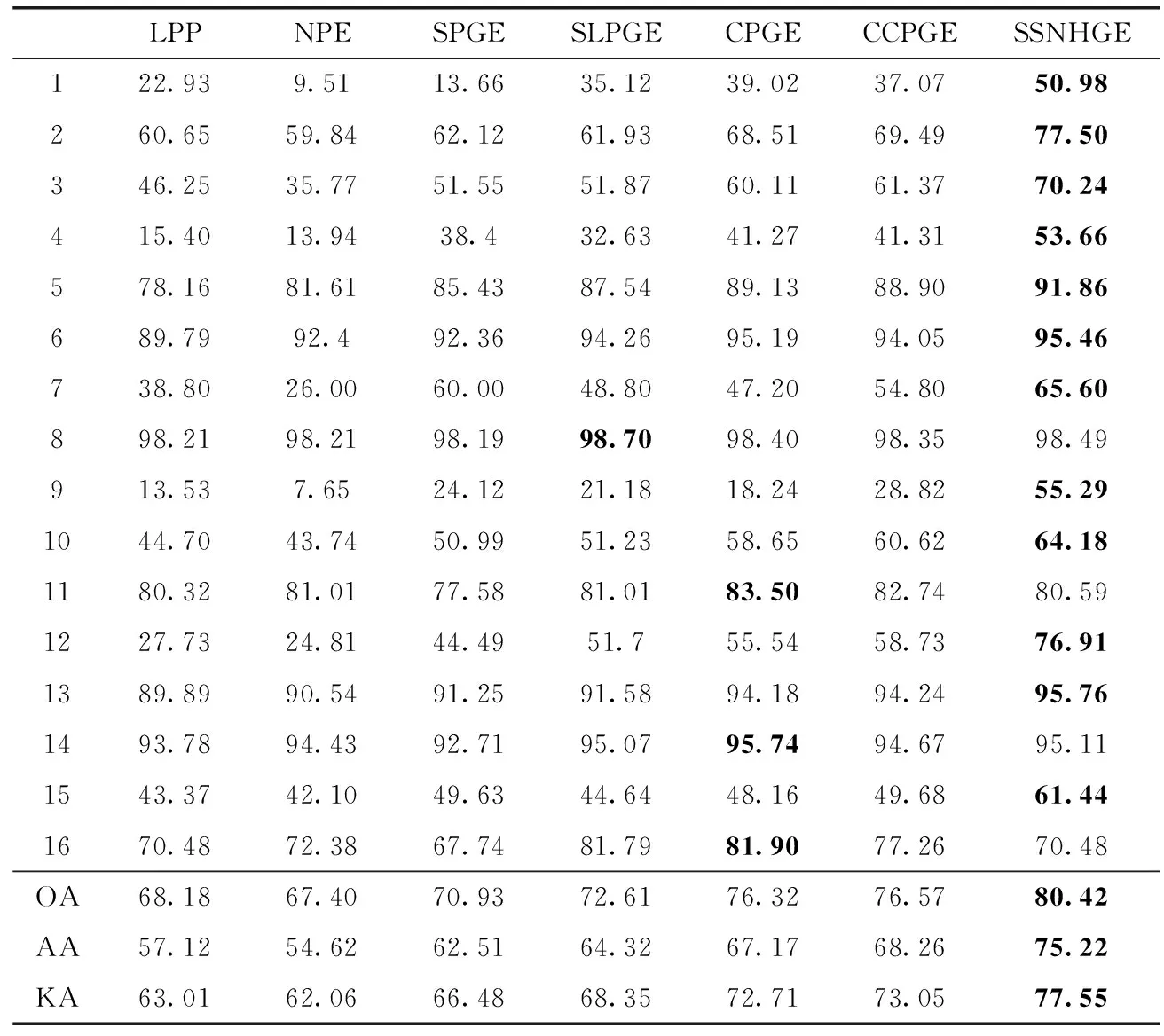
表4 各类算法在Indian Pines数据集的分类结果

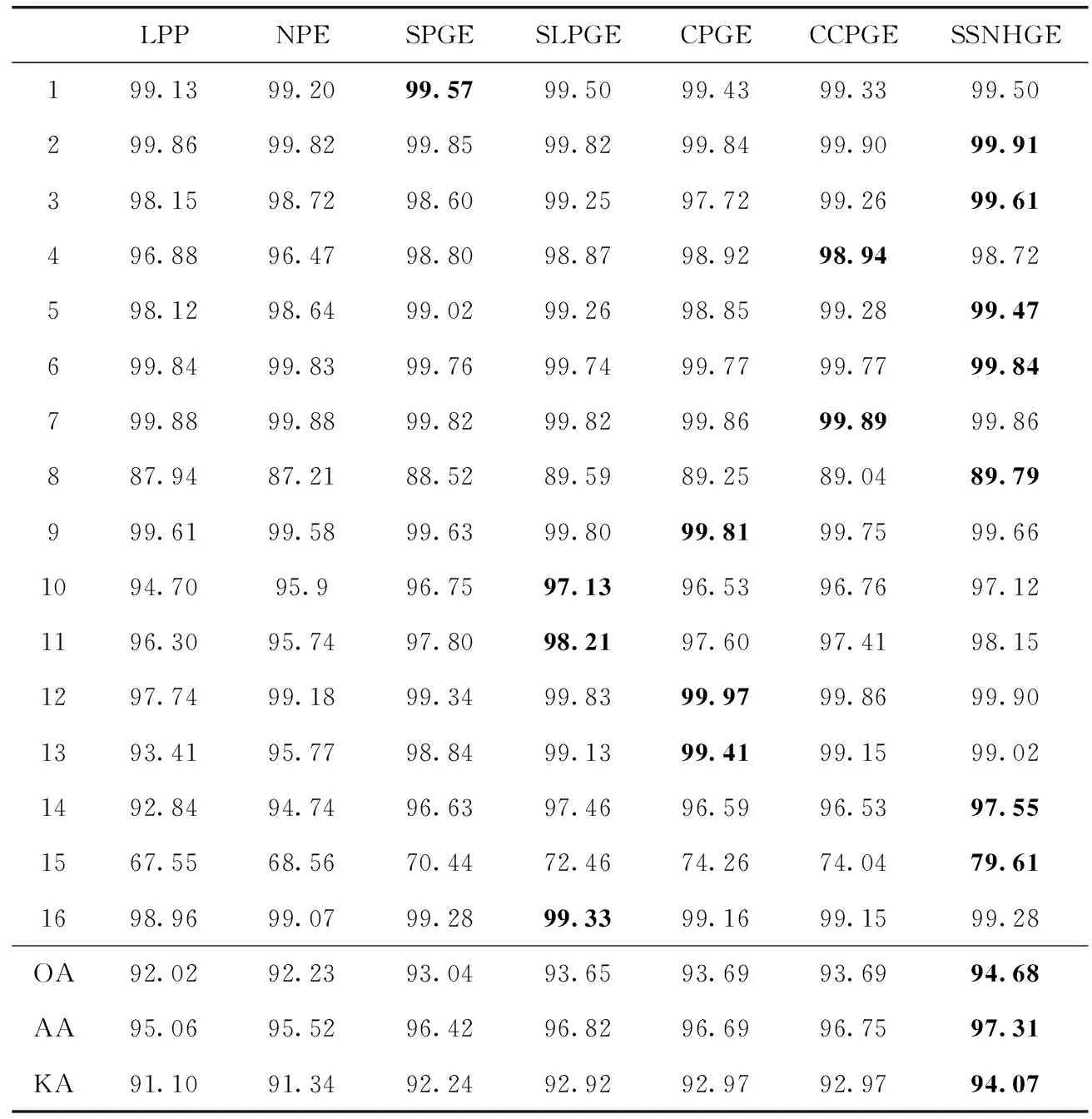
表5 各类算法在Salinas数据集上的分类结果

由表4可知，在Indian Pines数据集中，SSNHGE算法在大多数的地物分类中取得了较好的分类效果，评价指标OA、AA和KA在所有算法中是最好的。SSNHGE算法的OA为80.42%比CCPGE高3.85%，而传统的LPP只有68.18%；SSNHGE算法的AA为75.22%比CCPGE高6.96%，而传统的LPP只有57.12%，具有明显的优势，验证了SSNHGE算法的鲁棒性和有效性。在图7中，SSNHGE算法在“Corn-notill”，“Grass-pasture”和“Grass-trees”等区域错分点少，表现出了较好的效果，这是由于其它图嵌入算法仅考虑光谱信息进行构图，忽略了不同像元在空间上的关系。而所提算法有效地将空间信息融入，依据空间上距离越近，其像元越大的概率属于同类地物的原则，从距离较近的空间像元寻找光谱特征最相似的像元去构造无监督空谱近邻关系。通过该方法可有效地抑制噪点带来的影响，缓解同谱异物的问题，继而获得较好的分类效果。

图7 各类算法在Indian Pines数据集上特征提取后的分类结果

图8 各类算法在Salinas数据集上特征提取后的分类结果

各类算法在Salinas数据集上的分类性能见表5，SSNHGE算法对大部分地物都具较高的识别率，其OA、AA和KA指标同样优于其它各类算法。这说明与其它直接图嵌入算法对比，超图学习能够有效表征数据之间本征结构，揭示数据之间的内蕴关系，突出其鉴别特征。并且有效地融入空间信息后更有利于提取鉴别特征，提高地物分类性能。由图8可知，SSNHGE算法在“Fallow_smooth”，“Brocoli_green_weeds_2”和“Fallow”等区域错分点少，表现出了较好的效果，且地物分布效果平滑，进一步验证了所提算法的有效性。

最后，为探究训练样本对分类效果的影响，进行了一组不同的训练样本个数对分类精度的影响，并且在两个数据集上进行了验证。对于Indian Pines数据集，训练样本数量与总数量比为 {1/10，1/9，1/8，1/7，1/6}； Salinas数据集为 {0.01，0.02，0.03，0.04，0.05}。 如图9所示，各算法的分类精度与训练数据量成正比，验证样本信息越丰富，越能有效提取鉴别特征，其分类精度也就越高。同时，在Indian Pines数据集中，SSNHGE的分类精度明显优于其它算法，Salinas数据集在0.03之后也明显优于其它算法，说明与其它算法相比，所提算法能够达到更优的特征提取效果与分类效果。

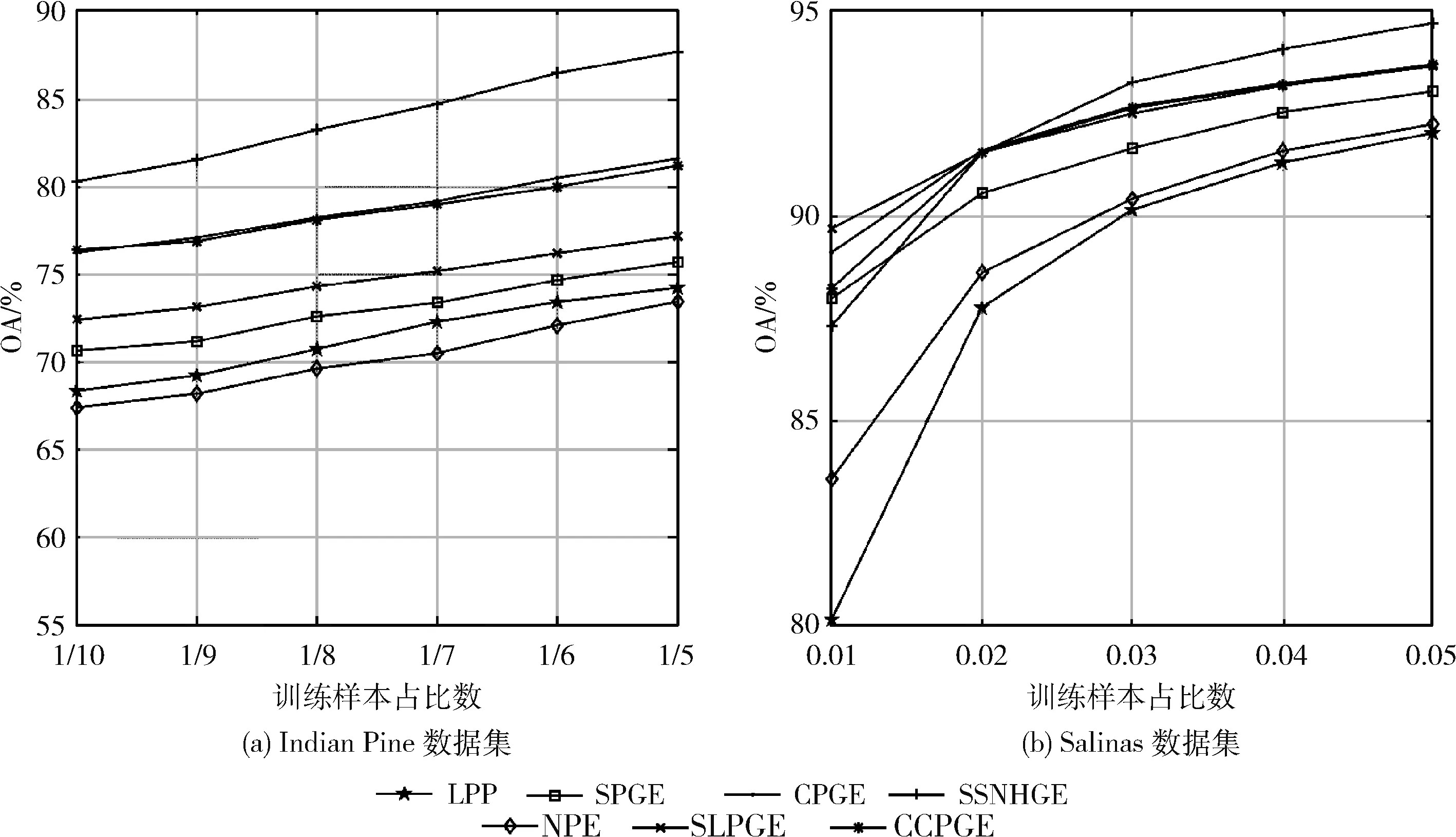
图9 维数d对总体分类的影响

3.4 算法运行时间对比

为了将SSNHGE算法与LPP、NPE、SPGE、SLPGE、CPGE和CCPGE算法的运行时间进行对比。选用Indian Pines数据集和Salinas数据集，在Intel(R) Core(TM) i5-8400处理器，16G内存平台上使用MATLAB进行实验。如表6所示，各类算法在Indian Pines和Salinas数据集上的运行时间，可以看出SPGE、CPGE、SLPGE和CCPGE这4个算法运行时间远高于SSNHGE算法，这是因为稀疏约束或低秩约束需要较大的计算资源。与SPGE、CPGE、SLPGE和CCPGE相比，SSNHGE算法的运行时间最少且分类性能最高。LPP、NPE和SSNHGE运行时间远低于其它图嵌入算法，SSNHGE算法的运行时间略高于LPP和NPE。但SSNHGE算法分类性能高于LPP和NPE算法。这是因为LPP和NPE算法仅利用局部信息构造图，而SSNHGE算法能够有效地融入空间信息并利用超图学习提取鉴别特征，提高地物分类精度。

表6 各类算法在Indian Pines和Salinas数据集上的运行时间

经过一系列的实验，将SSNHGE算法与其它无监督图嵌入特征提取算法对比，本文提出的无监督空谱近邻超图嵌入特征提取算法在地物分类准确性和运行时间方面都具有优势。

4 结束语

针对高光谱图像数据标注困难，空间和光谱信息利用不充分以及传统图嵌入无法表征高维数据之间复杂结构的问题，本文提出一种无监督空谱近邻超图嵌入特征提取算法，在无监督情况下，利用空间和光谱信息建立有效的近邻关系去构建超图模型，揭示高光谱数据的多元复杂关系，实现有效的鉴别特征提取。在公开的高光谱图像Indian Pines与Salinas数据集上进行一系列实验后，其实验结果表明，SSNHGE算法无论在分类精度上还是其它性能方面都优于同类算法。