传感器网中基于角度的移动目标跟测方法

李兰英，蒋维成，周 玲，黄 静

(成都理工大学工程技术学院 电子信息与计算机工程系，四川 乐山 614000)

0 引 言

无线传感器网络中，测定目标所在位置或范围比较复杂。常用的方法是测定目标与无线传感器之间的距离，利用目标与多个无线传感器之间的距离，通过计算得出目标的位置。这种方法投入监测的无线传感器数量较多，代价也高。目标在移动过程中距离发生改变，又须重新测量。如果目标是圆周上的移动，位于圆心位置的无线传感器，测得的距离却是不变的，这就导致测量无法反映目标的变化情况。然而采用角度的测量方式，很容易测得目标角度的变化。对移动轨迹呈圆周状、扇形，或不规则曲线的这类目标，采用角度的监测方法就具有一定优势。目标的移动往往是不规则的和复杂的，如野生动物的活动、罪犯或可疑目标在某区域的活动、独立作业机器的活动，对这类目标的监测，需要掌握目标的活动轨迹，不同时段的位移变化情况，以便对目标进行深入的分析研究。对于复杂的运动，若直接测定移动目标比较困难，可以测定水平和竖直两个方向的分运动，再通过对运动的合成而得到结果，就能把复杂的问题分解成两个相对简单的子问题来解决。采用位于不同方位且相距一定距离的多个无线传感器对目标进行角度测量，可以很容易得到目标在水平和竖直方向的移动，互相弥补，提高测量的准确度，完成复杂的监测任务。

1 相关研究

无线传感器网络在工农业生产和军事领域具有广泛的应用，吸引国内外众多的学者研究。文献[1]对传感器分布和布置进行研究，根据短期和长期的不同监控应用优化网络中的能量利用。文献[2]在考虑簇中结点分布和距离的基础上，对leach算法中成簇阶段簇头进行优化。文献[3]通过设定阈值，采用分层型拓扑控制算法，对网络能耗进行优化。文献[4]采用双簇头协作方案，减少故障，提高系统的可靠性。文献[5]根据能量和距离，对Dijkstra算法进行改进，实现能耗均衡。文献[6]利用综合链路质量指标，对路由协议进行优化，降低网络能耗。文献[7]根据实际和理论延时差值对排队延时进行估算，根据最大和最小排队延时阈值，对路由进行优化。文献[8]在短距离传输中采用光通信，在长距离传输中采用声通信，基于混合接收信号强度估计结点的位置。文献[9]把三维空间定位运算降为二维平面运算来对结点进行定位。文献[10]利用随机矩阵理论的谱分布定理和协方差矩阵奇异值分解性质实现对异常结点进行定位，提高准确性。文献[11]运用调度预处理，对链路比例冲突空余时间值分配时隙和信道资源，提高网络调度成功率。文献[12]采用跨层方法对网络进行优化，选择占空比大的结点来提高数据传输的可靠性，降低重传，提高能源效率。

这些算法对无线传感器网络资源的使用进行了优化，提高了效率。但缺少对网络中移动目标的研究。随着目标的移动，引起监测环境的改变和监测数据的有效性等问题，对移动目标的监测进行研究也是十分必要的。本文提出了基于角度的目标跟测方法(target tracking method based on angle，TTMBA)，采用所围区域中的关键结点对目标进行角度监测，相互弥补，并随目标的移动动态生成所围区域对目标进行有效监测。

2 算法框架

2.1 网络模型

无线传感器在监测区域内随机匀速地布置，各结点通过北斗定位系统或GPS获取其所在的位置。在无线传感器网络中为了保持对目标的有效监测，更好地研究目标在网络中的移动情况，本文讨论的模型抽象如下：

(1)假设目标是随机移动的，目标移动方向和移动速率具有不规则性。

(2)目标在无线传感器网络中所在的位置可以抽象为一个点。

(3)每个无线传感器均能实现0～360°角度的测量，并能对目标进行角度测量。

(4)无线传感器网络中的传感器密度符合要求，对目标进行有效监测，区域内无线传感器能有效通信。

2.2 区域内测定

以目标所在的位置为中心，其外围构成一个田字框，田字框的中心与目标重合或者附近。在平面内规定4个方向，x轴的正方向为东，负方向为西；y轴的正方向为北，负方向为南。并且假设田字框的所围区域是正方形。为讨论的方便假设正方形边长为1。位于4个角上的结点按方向称为东北角点、东南角点、西南角点、西北角点。位于北方水平线位置的边称为北方水平边，位于北方水平边中点位置的结点称为北方水平边中点。位于南方水平线位置的边称为南方水平边，位于南方水平边中点位置的结点称为南方水平边中点。位于东方竖直线位置的边称为东方竖直边，位于东方竖直边中点位置的结点称为东方竖直边中点。位于西方竖直线位置的边称为西方竖直边，位于西方竖直边中点位置的结点称为西方竖直边中点。田字框所围成的正方形区域称为所围区域，所围区域的中点位置称为所围区域中心。北方水平边中点和南方水平边中点的连线与东方竖直边中点和西方竖直边中点的连线将所围区域划分为4个子正方形区域。这4个子区域称为：所围区域东北子区、所围区域东南子区、所围区域西北子区、所围区域西南子区。

位于所围区域边界上角点位置和各边中点位置处的结点是关键结点。所围区域4个角点处的无线传感器确定位置后，就可以得知所围区域的位置。由于目标位于所围区域内，在确定所围区域的位置后，也就可以知道目标的大概位置。

设目标位置用L表示，无线传感器结点Sx监测目标具有的关系用ψ(Sx)表示，监测网可以描述如下

L=ψ(Si)∧ψ(Sj)∧ψ(Sk)

(1)

N(Si,Sj)=1,N(Si,Sk)=1

(2)

J(Si)=1

(3)

J(Sj)=0,J(Sk)=0

(4)

Si∝Min{dis(Si,c),dis(Sx,c)} (J(Sx)=1,x=u,v,w)

(5)

其中，N(Sx,Sy)表示无线传感器结点Sx与Sy是否为相邻结点，若相邻则为1，不相邻为0。J(Sx)表示无线传感器结点Sx是否位于角点，如果是位于所围区域的角点位置则为1，否则为0。式(2)、式(3)和式(4)表示结点Si与Sj和Sk相邻，Si位于角点，结点Sj和Sk不是角点。dis(Sx,c)表示无线传感器结点Sx与目标c之间的距离。

目标位置由所围区域关键结点中不同方位的3个无线传感器结点进行测量，一个位于角点位置，另两个与其相邻，但不是角点。目标同时满足这3个无线传感器监测到的结果，因而有式(1)。该角点在4个角点中距离目标的距离最近，因而有式(5)。

如果要进一步取得目标的位置，可以再对所围区域进行划分。南北水平边中点与东西竖直边中点的连线把所围区域划分成4个子正方形区域。在每个子正方形区域中，对角线之间的连线又将其划分成4个等腰直角三角形，所围区域中共有16个面积大小相同的等腰直角三角形。根据位置将所围区域内的等腰直角三角形划分为内圈等腰直角三角形和外圈等腰直角三形。内圈等腰直角三角形有一个顶点与所围区域的中心重合，位于所围区域的内部。外圈等腰直角三角形位于所围区域的外部。每个内圈等腰直角三角形外侧有一个外圈等腰直角三角形，内圈等腰直角三角形和外圈等腰直角三角形都是8个。

对所围区域内的等腰直角三角形进行编号，先对内圈等腰直角三角形进行编号，以所围区域的中心水平向东顺时针方向开始，每45°所对应的等腰直角三角形为一个编号，依次为0,1,2,3,4,5,6,7。外圈等腰直角三角形也按顺时针方向进行编号，与编号0相邻的外圈等腰直角三角形编号为8，与编号1相邻的外圈等腰直角三角形编号为9，以此类推。外圈等腰直角三角形的编号依次为8,9,10,11,12,13,14,15。这样所围区域中的16个等腰直角三角形按照一定规律编号成0～15。如图1所示，图中带圈的数字是等腰直角三角形的编号。

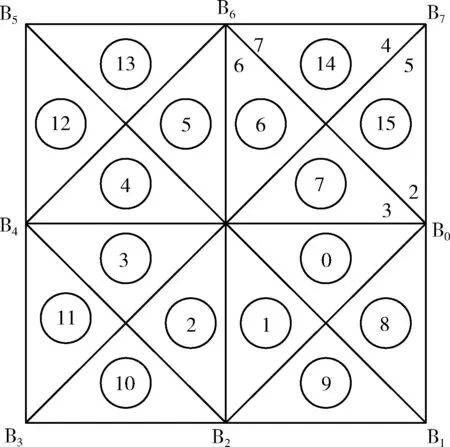
图1 所围区域

所围区域中的等腰直角三角形编号后，就可以方便地通过编号找到其所在的区域位置，或者通过区域位置找到相应编号。区域位置和编号之间的关系是一一对应的。

定义1 方向数：方向数是以无线传感器结点为中心，水平向东开始，逆时针方向旋转，每45°为一个方向数。其中：0～45°方向数为0，45°～90°方向数为1，90°～135°方向数为2，……，315°～360°方向数为7。整个平面划分为8个方向数，分别是0，1，2，3，4，5，6，7。

图1中所围区域中的东北子区由位于B0处的结点S0测得的方向数是2和3，位于B6处的结点S6测得的方向数是6和7，位于B7处的结点S7测得的方向数是4和5。

位于子区域中关键结点位置处的3个无线传感器监测到目标的方向数分别为θ1，θ2，θ3。子区域内的等腰直角三角形的编号可以由这3个结点测得的方向数来确定，通过适当变换转换成相应的区域编号。用L(d)表示目标所在位置的等腰直角三角形的编号。若目标处于内圈等腰直角三角形，则有式(6)

L(d)=(θ1+θ2+θ3)-7

(6)

若目标处于外圈等腰直角等腰三角形，则有式(7)

L(d)=(θ1+θ2+θ3)+1

(7)

当目标位于编号为6的等腰直角三角形区域时，位于B0，B6，B7处的无线传感器S0，S6，S7监测到的方向数分别是3，6，4。根据式(6)可得：L(d)=(3+6+4)-7=6，与该区域的等腰直角三角形编号6相同。目标位于编号为7的等腰直角三角形区域中时，无线传感器S0，S6，S7监测到的方向数分别是3，6，5。根据式(6)可得：L(d)=(3+6+5)-7=7，与该区域的等腰直角三角形编号7相同。当目标位于编号为15的等腰直角三角形区域时，无线传感器S0，S6，S7监测到的方向数分别是2，7，5。根据式(7)可得：L(d)=(2+7+5)+1=15，与该区域的等腰直角三角形编号15相同，其余等腰直角三角形的编号验证略。

原仅知道目标位于所围区域内，然而在对等腰直角三角形进行编号后，对目标进行方向数的测定，就可以进一步确定目标所在的区域，并将范围缩小到原来的1/16。

2.3 所围区域更新与运动合成

目标在区域内移动，在目标移出所围区域之前，需要对所围区域进行更新。新的所围区域根据目标所在的位置不同而分两种情况生成。这里以所围区域东南子区进行讨论。如图2所示，B’是东方竖直边中点B0和东南角点B1之间的中点，B’’是西方竖直边中点B4和西南角点B3之间的中点。B’B’’之间的连线将所围区域东南子区划分为两部分。第一种情况，目标即将移出时位于所围区域东南子区B’B’’连线以北。第二种情况，目标即将移出时位于所围区域东南子区B’B’’连线以南。第一种情况中，目标的移动位置位于所围区域东方竖直边附近的中部，新生成的所围区域应尽可能以目标为中心，新的所围区域是把原所围区域水平向东平移边长的1/2距离。原所围区域中B0位置处将成为新的所围区域中心。第二种情况中，目标移动位置位于所围区域的东南方向，新的所围区域是把原所围区域水平向东平移边长的1/2，然后再竖直向南平移边长的1/2距离。原所围区域中结点B1位置处将成为新的所围区域中心，这样生成的所围区域也尽可能以目标为中心。

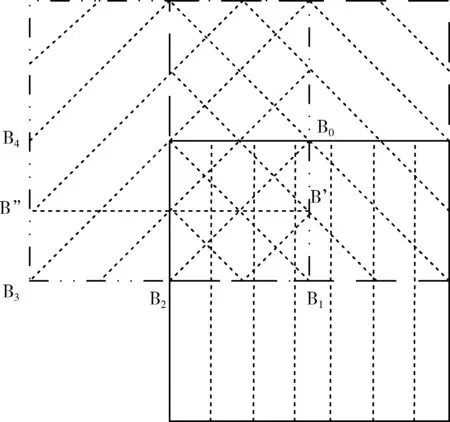
图2 更新所围区域

新生成的所围区域充分考虑了目标的移动方向和运动趋势的需要。目标在第一种情况中向东、东北、东南方向移动，生成的所围区域中有1/2面积可以为目标提供活动范围。目标在第二种情况中向东、东北、东南或转变为向南方向移动，生成的所围区域中有3/4面积可以为目标提供活动范围。

上述两种情况生成的所围区域与原所围区域存在重叠部分，也就是原所围区域中有部分区域保留在新生成的所围区域中。目标当前停留在这部分区域中，由于移动的不确定性，目标可能返回到以前的位置或者附近。保留这部分区域是为了在目标出现这种情况时也能很好地进行监测。

第一种情况生成的所围区域中，原所围区域中东南角点B1和南方水平边中点B2这两个点成为新生成的所围区域的关键点。第二种情况生成的所围区域中，原所围区域中东方竖直边中点B0和南方水平边中点B2这两个点成为新生成的所围区域的关键点。在这两种情况中，原所围区域中的8个关键结点有且仅有2个关键结点在新的所围区域中，有利于将上一阶段的有关信息保留传递到下一阶段的监测任务中去。另有6个关键结点不再是新的所围区域中的关键结点，可以避免结点能量消耗过多而提前死亡。

这里是以所围区域东南子区为例进行讨论的，由于正方形区域具有对称性，其它子区的情况类似，不再叙述。

要确定目标所在的具体位置，还需要测定目标所在位置角度的大小。这里以所围区域东南子区进行讨论。如图3所示，若目标位于R处，R与南方水平边中点B2之间的连线同南方水平边之间的夹角为α，R与东南角点B1之间的连线同南方水平边之间的夹角为β，R与东方竖直边中点B0之间的连线同东方竖直边之间的夹角为γ。R’为R在南方水平边上的垂足。R’’为R在东方竖直边上的垂足。由于所围区域的边长为1，B1，B2之间的距离为1/2。那么可得

|RR′|=|B2R′|·tanα

|RR′|=(1/2-|B2R′|)·tanβ

因此，可以进一步得到R与南方水平边的距离Dv和与东方竖直边的距离Dh

(8)

(9)

R与所围区域中点B0,B1,B2之间的距离分别为

图3 角度

若t0时刻，R与南方水平边中点B2之间连线与南方水平边之间的角为α0，t1时刻为α1。若t0时刻，R与东南角点B1之间连线与南方水平边之间的角为β0，t1时刻为β1。若t0时刻，R与东方竖直边中点B0与东方竖直边之间的角为γ0，t1时刻为γ1。

根据式(8)和式(9)可得目标在(t0,t1)时间里在竖直方向的位移增量ΔMv和水平方向的位移增量ΔMh分别为

当ΔMv>0时，t1时刻距离南方水平边的距离比t0时刻要大，目标向北方向移动。当ΔMv<0时，目标向南方向移动。

当ΔMh>0时，t1时刻距离东方竖直边的距离比t0时刻要大，目标向西方向移动，当ΔMh<0时，目标向东方向移动。

由水平位移增量和竖直位移增量可以合成目标的位移增量ΔM′，从而有

(10)

位移改变量的角度为φ，并且有

(11)

若知道t0时刻目标的位移，根据式(10)和式(11)可以得到t1时刻的位移。如果对目标进行多次监测，就可以得到这段时间的运动轨迹，以及不同时刻的水平位移增量和竖直位移增量的变化情况，在这两个分量的基础上，合成目标的位移，从而对目标移动过程的不同时刻运动改变情况进行深入的分析，掌握目标的详细移动情况。

这里是以所围区域东南子区为例进行讨论，由于正方形具有对称性，其它子区的情况类似，也不再叙述。

若知道目标在(tn-1，tn)时间和(tn，tn+1)时间里目标的位移改变情况。根据这两段时间的位移增量，预测(tn+1，tn+2)时间的位移增量。

如果(tn，tn+1)时间的位移增量和(tn-1，tn)时间的位移增量相同。预测下一段时间(tn+1，tn+2)位移增量也相同。

如果(tn，tn+1)时间的位移增量比(tn-1，tn)时间的位移增量大，预测下一段时间(tn+1，tn+2)位移增量也将增大，增大量与时间成正比。

如果(tn，tn+1)时间的位移增量比(tn-1，tn)时间的位移增量小，预测下一段时间(tn+1，tn+2)位移增量也将减小，减小量与时间成正比。

设置两个阈值h1和h2，对于不同的应用系统，可以根据环境设置不同。当目标距离所围区域的边界距离小于或等于h1时，对目标的位移方向和位移改变大小进行预测。

若目标的位移改变有利于增加目标移出所围区域的概率，预测目标下一个时段的位置。如果预测位置距离边界的值小于阈值h2，根据对目标的预测位置，符合第一种情况，按第一种情况生成所围区域；符合第二种情况，按第二种情况生成所围区域。

若目标的位移方向发生改变或移动速率减小，导致目标在下一时段移出所围区域概率减小，过一段时间再检查目标的移动情况，进行决策。如果目标在下一时段的位置小于阈值h2，则根据目标的位置生成所围区域。

3 仿真结果

采用Matlab软件构建算法模型，对本文算法和leach算法进行比较实验。为了模拟现实环境中不同情况下的执行效果。实验过程中采用不同的参数进行了多次实验，对无线传感器网络生存期中的有关参数进行了详细实验。图中的TTMBA是本文所提出算法。

(1)网络中无线传感器结点死亡数比较

无线传感器在执行监测任务的过程中不断地消耗能量，无线传感器死亡数增多，网络中担任监测任务的无线传感器就越少，导致无效数据增加，重复监测增多，加重网络通信的负担，对任务监测和网络通信都不利。

两算法中无线传感器死亡数随时间的变化情况如图4所示。从图4可以看出，在相同的时刻leach算法中死亡数比本文算法要多，本文算法在目标的移动过程中不断生成新的所围区域，更换监测的无线传感器，考虑了能量的均衡利用。避免部分结点能耗过度提前死亡。因而网络中的无线传感器死亡数要少。

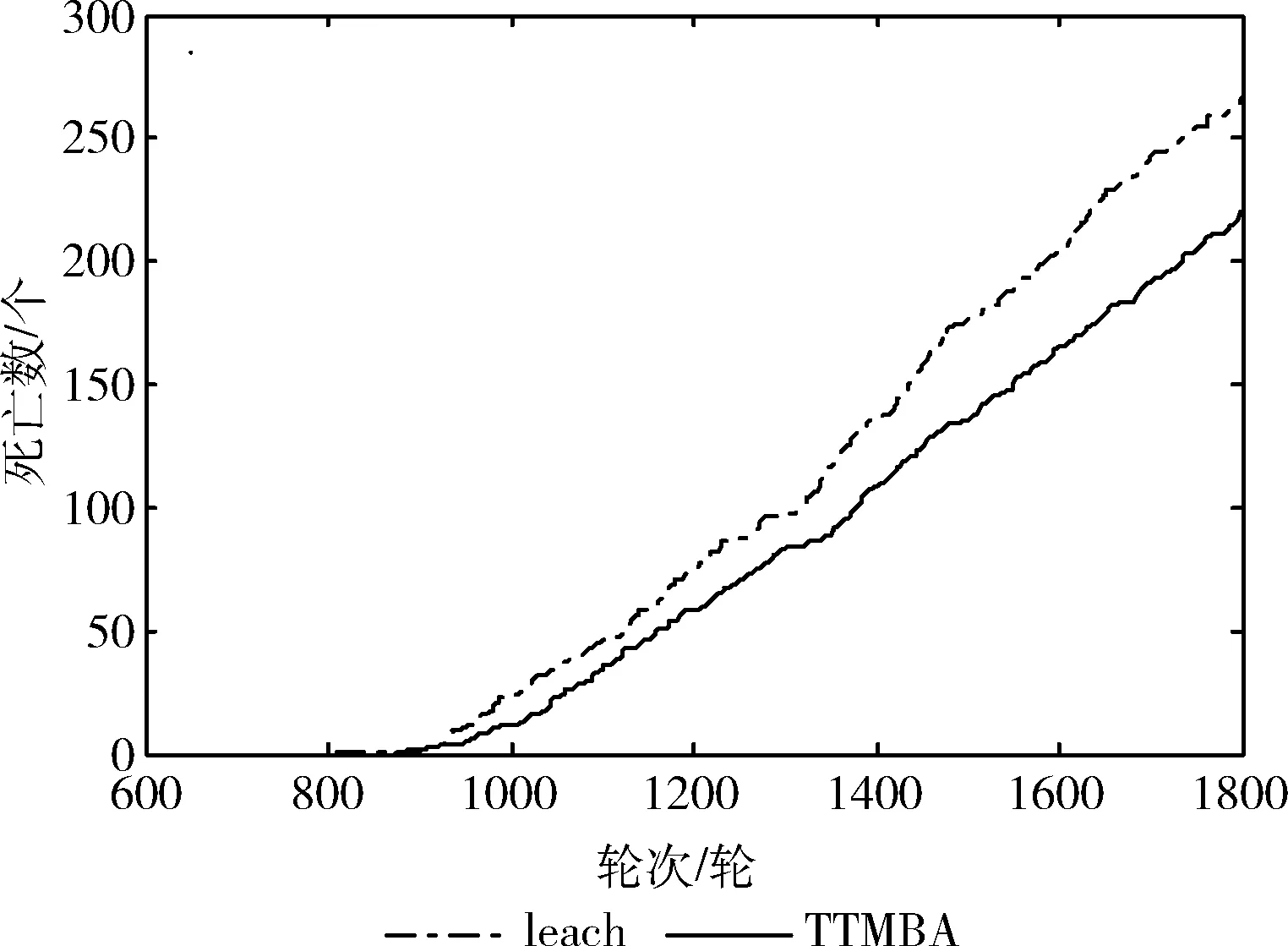
图4 死亡数比较

(2)网络中无线传感器结点存活数比较

无线传感器网络中监测需要存活的无线传感器来完成，无线传感器存活数越多，网络中剩余能量也越多，目标的监测也就能持续有效进行，获得更多的有效数据，网络中能量的利用率也就越高。

在执行相同的监测任务情况下，两算法中无线传感器结点存活数随时间的变化情况如图5所示。从图5可以看出，在相同的时间里，本文算法要比leach算法存活数要多。本文算法在目标附近生成所围区域，仅由目标附近的无线传感器进行监测，提高了监测的准确性和监测的效率，减小了不必要的能量损耗，因而网络中的存活数要多。

图5 存活数比较

(3)网络中无线传感器死亡百分数的比较

无线传感器网络有效期跟网络中结点死亡百分比有很大关系。监测任务的完成需要网络中具有一定数量的无线传感器。随着网络中无线传感器死亡数的增加，将出现某个时刻对移动目标无法监测，监测数据无法及时回传给Sink结点，网络中结点通信间断或中断，导致网络有效期缩短。两算法中无线传感器死亡4%、9%、14%时的比较如图6所示。从图6可以看出，本文算法在这3种死亡百分比情况下均比leach算法时间要晚，表明本文算法的网络有效生存期更长。本文算法中所围区域是根据地理位置生成的。而leach算法中簇头选举和轮换及相关通信都需要消耗能量，此外本文算法考虑能量的均衡利用。因而在结点死亡4%、9%、14%这3种情况下均比leach算法要晚。

图6 死亡百分比

4 结束语

获取目标的位置具有重要意义，可以对目标进行有效的监测。本文采用所围区域上的关键结点基于角度测量方法进行监测，通过对所围区域中的等腰直角三角形进行编号，运用方向数和编号之间的映射关系，实现目标的快速区域定位。采用角度的测量方法，获取目标水平位移增量和竖直位移增量，合成目标的位移，详细掌握目标的移动情况。根据目标的移动，动态生成所围区域。新生成的所围区域有较大范围满足目标的移动趋势的需要，同时与原所围区域存在一定的重叠部分，可满足目标返回上一状态位置监测的需要。不同方位的无线传感器基于角度的测量方法对目标进行监测，相互弥补，使得对目标的监测更加准确。