时速100公里级地铁车辆通过隧道时引起的活塞风仿真研究
朴荣焕,张继业,李田
时速100公里级地铁车辆通过隧道时引起的活塞风仿真研究
朴荣焕,张继业,李田
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
地铁车辆通过隧道时,会诱导隧道内气体流动,对隧道内通风、基础设备运行以及人员安全造成安全隐患。为确保隧道内设备正常运行与人员安全,针对地铁车通过隧道时引起的气体流动进行研究。本文使用仿真计算的方法,基于滑动网络技术数值模拟某一地铁车辆通过隧道的动态过程,监测地铁车辆通过隧道时引起的隧道内气体流动。结果表明:隧道内活塞风纵向分量和总流量变化基本一致,隧道内的活塞风主要是纵向流;距离车体或地面越远,列车风流速最大值越小;车底与车顶处活塞风沿垂向距离降低缓慢,车体中部活塞风流速沿垂向迅速降低;隧道内活塞风流速最大值出现在距离入口750 m处。
地铁车辆;隧道滑流;压力波
高速列车运行时,由于空气的粘性,运动列车会带动车体周围空气运动,称为列车风。目前对于明线运行时车体周围的列车风进行了广泛研究,特别是车头几何形状、列车长度、列车速度等因素对车体周围流畅的影响[1-4],同时有研究指出,列车风的强度在横向和垂直方向上与车体的距离高度相关[5]。而当高速列车从外部环境进入隧道时,列车周围的空间急剧缩小。由于隧道壁面的限制,当列车头部进入隧道时,在车头前方形成高压区,产生压缩波,推动空气向前运动;当列车尾部进入隧道时,尾部后部会形成低压区,产生膨胀波,将外部空气吸入隧道,这种由运行列车所驱使的空气运动被称为活塞效应[6]。活塞效应引起的气流会对隧道内的通风机、接触网系统和横向通道的安全门等装置产生较大的瞬态压力,影响设备正常运行,同时会对轨旁工作人员造成潜在的安全隐患。陈逸斐[7]通过有限元模型对地铁车辆端部底架疲劳强度进行虚拟试验。而针对隧道内滑流对人员及设备的危害,欧盟国家共享一套规则,指出根据列车在两个高度(0.2 m和1.4 m)下的最大合成允许水平风速[8];在日本,安全站立距离基于9 m/s滑流平均速度[9];在中国,考虑到安全问题,14 m/s速度被视为滑流极限[10]。刘堂红等[11]对隧道中的列车诱导的列车风进行了现场测量,发现流畅速度大小与列车速度呈线性关系。列车通过隧道时产生的气流基本上是三维的,在纵向、横向及垂向都有分量。由于隧道的纵向长度远远大于横向宽度,在隧洞中传输的压力波可近似视为一维平面波[12]。滑流强度与车头流线型形状、列车运行速度和距离车体的横向距离有关,而地铁车辆相较于高速列车,其头型流线型更小且隧道直径较小,会产生剧烈的压力波动和气体流动。因此为确保地铁车隧道内的人员安全及隧道内设备的安全,需要对地铁车通过隧道时引起的隧道内滑流进行研究。
1 仿真方法
1.1 几何模型
地铁车模型为六节车模型,最高运营速度为100 km/h。车辆部件包括空调、转向架、车钩和风挡等,如图1所示。由于车灯等结构对此研究结果影响很小,建立几何模型时进行了简化处理。此模型车长为141 m,车宽为3.1 m,车高为3.8 m,纵向截面面积10.28 m2。隧道为圆形隧道,隧道截面直径为6 m。

图1 地铁及其车模型
1.2 计算域及边界条件
计算域入口与出口处采用半圆形计算域,半圆形区域半径为50 m、长度为500 m,列车头车距离入口距离为50 m。根据隧道内最大负压峰值,隧道长度是列车运行的最不利长度[16-17],计算公式为:

式中:l为列车长度,m;为当地声速,m/s;v为列车列车运行速度,m/s。
计算区域分为两个部分:区域Ⅰ为包含列车的细长半圆柱形,而区域Ⅱ包括外部区域和部分隧道区域,如图2所示。列车与隧道的相对运动采用滑移网格实现。滑移网格法目前被证明是模拟列车通过隧道时产生的相互作用最有效方法之一[13]。与动网格相比,滑移网格不需要变化网格,在确保精度的前提下大大提高了网格质量和计算效率。区域Ⅰ与区域Ⅱ的边界采用交界面传输信息。
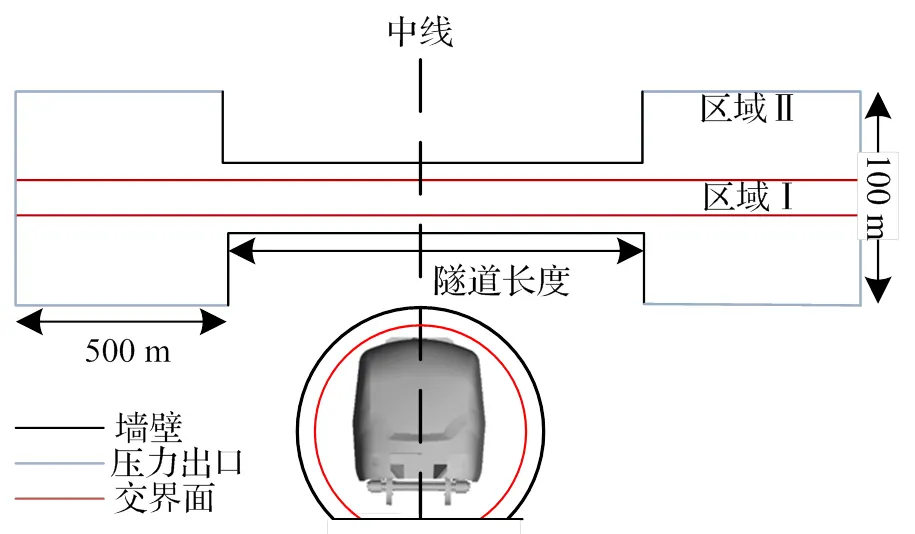
图2 边界条件设置
为了避免压力波在外部边界上的反射,将外部计算域的顶面、侧面和背面定义为压力出口。列车表面、地面和隧道表面被定义为静止的防滑壁边界。坐标系原点位于隧道入口地面中点,轴沿隧道纵向,轴沿隧道横向,轴沿隧道垂向。
1.3 网格划分
由于列车具有复杂的几何结构,包括转向架、空调和风挡等,因此,Ⅰ区采用四面体网格,Ⅱ区采用结构网格生成六面体网格。在网格划分中,为了准确地模拟车体周围的流场变化,列车附近流场区域采用四面体网格、且对曲面变化较大的部分进行加密处理。同时外部计算域靠近隧道端流场进行轴向加密处理,横向沿指向隧道入口与隧道出口方向进行加密。网格划分的结果如图3所示,总网格数量约为2400万。

图3 计算域及车体网格
1.4 求解器
由于活塞效应,列车通过隧道时引起的气体流动为非定常流动,气体模型采用理想可压缩气体,湍流模型选择Rng k-e。有研究证明,该方法在模拟列车通过隧道时引起的气动效应是有效的[13-15],在大多数情况下,相关应用和验证的工作与移动模型或全尺寸实验数据的最大差异都在5%以内。控制方程采用连续性方程、Navier-Stokes方程和能量方程,分别描述了质量守恒、动量守恒和能量守恒的物理关系。壁面函数采用尺度化壁面函数,采用压力基的PISO算法依次迭代方程组中的压力、速度项。由于高压驱动气流运动,采用PRESTO!算法离散压力项,有利于捕捉初始的高、低压界面流动。密度、动量及能量方程采用二阶迎风格式。为加快收敛,采用二阶隐式的对偶时间步推进方法离散时间项,以增大时间步迭代的稳定性时间步长设为0.005 s,总时间步数以头车到达出口计算域边界为标准,每步迭代20次。
1.5 监测点布置
监测点横向位置以及所在的纵向平面如图4所示,监测点距离车体中轴线分别为1.7 m、2.2 m与2.7 m。垂向距离以地面为基准,每间隔0.5 m设置一个监测点,分别位于左右两侧,监测纵向流速分量v、横向流速分量v与垂向流速分量v。
总滑流计算式为:
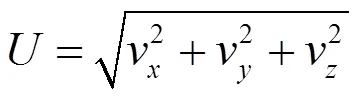
1.6 网格独立性检验
综合考虑选择合适的网格尺寸,Mesh1采用细网格,Mesh2采用粗网格,体网格最大尺寸均为500 mm,车体面网格尺寸和总网格数量如表1所示。隧道长度采用上节提到的最不利隧道长度1075 m,对比隧道中点监测点处列车风数据,如图5所示,可见,两种网格计算的结果趋势相同,尾车通过监测点时粗网格与细网两种网格尾流流速峰值分别为21.9 m/s和22.4 m/s、误差为2.2%,在可接受范围内,所以后续工况采用粗网格尺寸进行模拟仿真。

表1 粗网格与细网格网格尺寸与网格数量
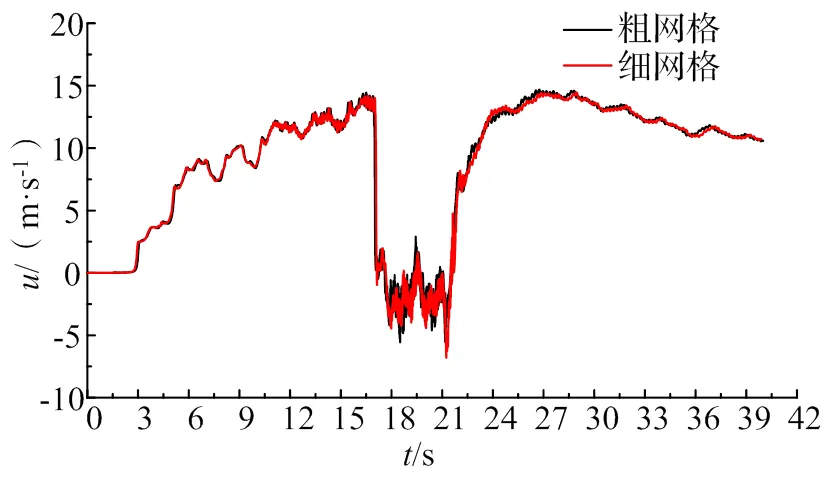
图5 粗网格与细网格计算结果对比
1.7 模型验证
文献[16]中进行了地铁车辆实车试验,监测了隧道内表面气体流速,将文献中的结果与仿真结果进行对比,仿真结果与试验数据相吻合,如图6所示。由于文献[16]中隧道内存在初始风速,而仿真中没有考虑隧道内的初始风速,所以列车通过监测点前的结果不吻合,但当尾车通过监测点后实验结果与仿真结果一致,可以说明此研究方法是可靠的。

图6 仿真数据与实验数据对比
2 结果与分析
2.1 流动方向
图7绘制了隧道中点处纵向流速分量v、横向流速分量v和垂向流速分量v与总流速的关系。由于总流速永远为正值,可以看出,纵向流速分量v与总流速的绝对峰值相同,且横向流速分量v与垂向流速分量v相对相对较小,经过平方根计算后可以忽略不计,说明隧道内的气体流动主要为纵向流动,与文献[12]所提出的结论相同,因此在以下的分析中,主要针对纵向滑流进行分析。
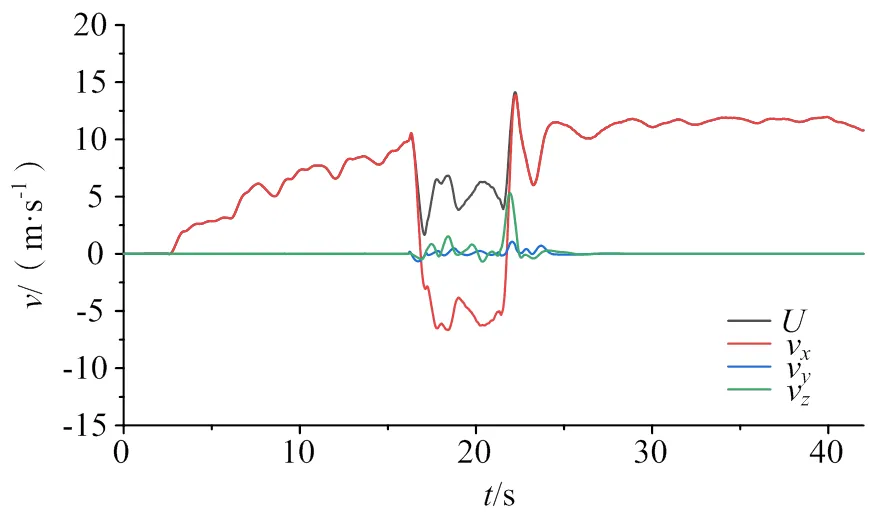
图7 各滑流分量对比
2.2 同一纵向截面
图8(a)(b)(c)分别绘制了距离隧道中轴线1.7 m、2.2 m和2.7 m不同高度监测点位置的列车风流速,图8(d)绘制了距离地面2.5 m不同水平距离监测点处测得的风速,1时刻与2时刻分别为头车鼻尖通过监测点与尾车鼻尖通过监测点时刻。

图8 同一截面纵向滑流对比
从图8可以看出,隧道内活塞风的最大值均出现在尾流处,并且随着横向距离的增加、尾流流速最大值降低。同时,隧道风速对横向距离的敏感程度低于垂向距离,与文献[17]中明线运行情况的结果不同,主要是因为露天环境没有壁面限制,隧道内受隧道壁面的干预,致使隧道内气体流动主要受活塞效应与摩擦效应的影响,而隧道内横向相较于垂向受到更多限制,所以隧道内气体流速对垂向距离更加敏感。当地铁车辆通过时,隧道壁面与车体壁面之间形成涡流,导致靠近隧道壁面处气体流动方向与地铁车辆运行方向相反。
2.3 隧道内活塞风特性曲线
图9绘制了列车中点处纵向截面流速云图,可知:由于车底部分转向架与车底设备的影响,底部区域气流流速快且峰值几乎不变;车顶及其以上部分,由于空间大且车顶设备较少,此处气流流速受车体运动影响较小,所以随着高度的增加峰值下降平缓;而车体中部由于靠近车体,受车体侧壁的影响,随着垂直高度的增加,气体流速峰值迅速降低。车底与车顶部分为缓慢下降区域,中部为快速下降区域。
根据此平面距离中轴线2.2 m监测点气体流速可拟合快速下降区的活塞风曲线,拟合公式见式(3),描述了距离中轴线2.2 m处隧道内气体流速与高度的相互关系,可以看出,在列车中部附近气体流速对于高度位置最敏感,此敏感性与隧道形状、车体形状等因素有关。

2.4 隧道内压力波
为分析隧道内压力波的作用,分析隧道入口监测点、隧道内监测点以及隧道出口监测点气体流动情况,如图10所示。其中N与T分别代表头车鼻尖与尾车鼻尖位移,黄色直线代表与列车同向压力波,实线为压缩波,虚线为膨胀波,蓝色直线代表与列车反向压力波,实线为压缩波,虚线为膨胀波。

图9 沿垂向高度局部气流流速变化
从图10可以看出,由于车头进入隧道时引起压缩波效应,气体流动速度在N到达之前就开始上升,1时刻头车进入隧道,此时头车经过隧道入口监测点,压缩隧道内气体从而产生压缩波;2时刻尾车经过隧道入口监测点,产生膨胀波;3、4分别为头车经过隧道内监测点与隧道出口检测点时刻;5、6分别为尾车经过隧道内监测点与隧道出口检测点时刻。此外,红色直线标注了膨胀波与压缩波传播方向与列车同向的时刻,绿色直线标注了膨胀波与压缩波传播方向与列车反向的时刻,可以看出同向时,膨胀波会加速隧道局部流量,压缩波会降低隧道内的局部气体流速,而反向时膨胀波会降低隧道局部流量,而压缩波会提升隧道局部气体流速。

图10 马赫波对隧道内局部气流的影响
2.5 人员安全退避距离
文献[10]中确定人员安全距离的标准为列车尾部最大风速不超过14 m/s。绘制距离隧道中轴线2.7 m位置隧道风风速峰值变化,并进行二次曲线拟合,如图11所示。
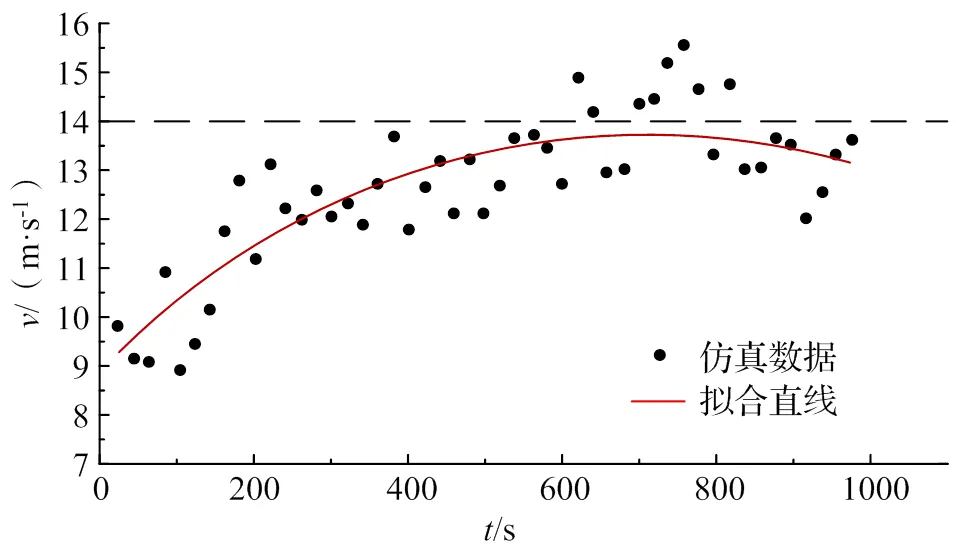
图11 距离中轴线2.7 m活塞风风速峰值
从图11可以看出,隧道内列车风风速峰值随着列车运行位置增加,在距离入口750 m时达到最大值,随后在距离入口750 m至隧道出口期间呈现下降趋势。在接近隧道出口位置部分已经超过规定速度,因此在列车以100 km/h运行时,不建议人员在隧道内进行作业。
3 结论
采用非定常方法对某地铁车通过隧道时产生的活塞风进行了CFD研究,结果总结如下:
(1)列车诱导的活塞风为三维流动,活塞风纵向分量和总流量变化基本一致,且纵向流量远大于横向流量和垂向流量,说明隧道内的气体流动主要是一维纵向流。
(2)隧道内的压力波对局部气流有一定的影响。当压力波的传播方向与列车运行方向相同时,压缩波的到来加速了局部气体流速,而膨胀波则使其减小。当压力波的传播方向与列车运行方向相反时,压缩波的到来降低了局部气体流速,而膨胀波增强了局部气体流速。
(3)活塞风纵向流量的最大峰值随垂直高度的增加而减小,由于侧向空间有限,流速最大峰值对侧向距离的敏感性小于垂直高度,纵向流量的最大峰值随侧向距离的增大而减小。车辆底部区域气流流速快且沿垂向变化缓慢,车顶部分及其以上部分气流随着高度的增加峰值下降平缓,而车体中部由于靠近车体,气体流速迅速下降。
(4)当车速达到100 km/h时,隧道内活塞风流速最大值已经超过14 m/s,根据人员安全退避距离,未达到安全标准,因此在列车运行时,不建议隧道内人员作业。
[1]XIE Taizhong,LIU Tanghong,CHEN Zhengwei,et al. Numerical study on the slipstream and trackside pressure induced by trains with different longitudinal section lines[J]. Journal of Rail and Rapid Transit,2018,232(6):1671-1685.
[2]CHEN Zhengwei,LIU Tanghong,YAN Chunguang,et al. Numerical simulation and comparison of the slipstreams of trains with different nose lengths under crosswind[J]. Journal of Wind Engineering & Industrial Aerodynamics,2019(190):256-272.
[3]GUO Zijian,LIU Tanghong,CHEN Zhengwei,et al. Comparative numerical analysis of the slipstream caused by single and double unit trains[J]. Journal of Wind Engineering & Industrial Aerodynamics,2018(172):395-408.
[4]WANG Shibo,Bell J R,Burton D,et al. The performance of different turbulence models (URANS, SAS and DES) for predicting high-speed train slipstream[J]. Journal of Wind Engineering & Industrial Aerodynamics,2017(165):46-57.
[5]GUO Zijian,Liu Tanghong,Chen Zhengwei,et al a. Comparative numerical analysis of the slipstream caused by single and double unit trains[J]. Journal of Wind Engineering & Industrial Aerodynamics,2018(172):395-408.
[6]CROSS D,HUGHES B,INGHAM D,et al. Enhancing the piston effect in underground railway tunnels[J]. Tunnel and Underground Space Technology,2017(61):71-81.
[7]陈逸斐. 地铁车辆端部底架疲劳寿命研究[J]. 机械,2021,48(1):44-51.
[8]BS EN 14067-4:Requirements and Test Procedures for Aerodynamics on Open Track[S].
[9]LIAO S,et al. Aerodynamic Effects of High-Speed Trains on People and Property at Stations in the Northeast Corridor[R]. United States:Federal Railroad Administration,1999.
[10]田红旗. 中国列车空气动力学研究进展[J]. 交通运输工程学报,2006(1):1-9.
[11]刘堂红,田红旗,金学松. 隧道空气动力学实车试验研究[J].空气动力学学报,2008(1):42-46.
[12]梅元贵,王瑞丽,许建林,等. 高速列车进入隧道诱发初始压缩波效应的数值模拟[J]. 计算力学学报,2016,33(1):95-102.
[13]NIU Jinqiang,ZHOU Dan,LIU Feng,et al. Effect of train length on fluctuating aerodynamic pressure wave in tunnels and method for determining the amplitude of pressure wave on trains[J]. Tunnel and Underground Space Technology,2018(80):277-289.
[14]WANG Yiwei,YANG Guowei,HUANG Chengguang,et al. Influence of tunnel length on the pressure wave generated by high-speed trains passing each other[J]. Science China Technological Sciences.,2012,55(1):255-263.
[15]CHEN Xiaodong,LIU Tanghong. ZHOU Xisai,et al. Analysis of the aerodynamic effects of different nose lengths on two trains intersecting in a tunnel at 350 km/h[J]. Tunneling and Underground Space Technology,2017(66):77-90.
[16]ZHANG Na,LU Zhaijun,ZHOU Dan. Influence of train speed and blockage ratio on the smoke characteristics in a subway tunnel[J]. Tunneling and Underground Space Technology,2018 (74):33-40.
[17]HUANG Sha,HEMIDA Hassan,YANG Mingzhi. Numerical calculation of the slipstream generated by a CRH2 high-speed train[J]. Journal of Rail and Rapid Transit. 2016(230):103-116.
Simulation Study on Piston wind Caused by 100 km/h Metro Vehicles Passing through Tunnels
PIAO Ronghuan,ZHANG Jiye,LI Tian
( State Key Laboratory of traction power, Southwest Jiaotong University, Chengdu 610031, China )
Metro vehicles passing through the tunnel induce the air flow, which will cause hidden danger to the ventilation in the tunnel, the operation of equipment and the safety of personnel. In order to eliminate these hidden dangers, this paper carries out a simulation study on the air flow caused by metro vehicles passing through the tunnel. The dynamic process is simulated by using the sliding mesh technology, and the airflow is monitored. The results show that the longitudinal component of piston wind in tunnel is consistent with the total flow, and the piston wind in tunnel is mainly longitudinal flow. The farther away from the car body or the ground, the smaller the maximum value of train air flow velocity. The piston wind at the vehicle bottom and roof decreases slowly along the vertical distance, but decreases rapidly in the middle of the car body. The maximum value of piston air flow velocity in the tunnel appears at 750 m away from the tunnel mouth.
metro vehicles;tunnel slipstream;pressure wave
U270.2
A
10.3969/j.issn.1006-0316.2021.11.006
1006-0316 (2021) 11-0041-08
2021-04-12
国家重点研发计划(2016YFB1200403);国家自然科学基金(51605397)
朴荣焕(1996-),男,内蒙古呼伦贝尔扎兰屯市人,硕士研究生,主要研究方向为列车空气动力学与耦合动力学,E-mail:piaoronghuan@126.com。*通讯作者:张继业(1965-),男,四川夹江人,博士,教授,主要研究方向为高速列车空气动力学,E-mail:jyzhang@swjtu.edu.cn。

