基于自组织神经网络的科技成果转移预测模型与仿真

王春嬉， 甘娟， 马龙

(西安航空学院 经济管理学院，陕西 西安 710077)

0 引言

近年来，我国对于科技创新的支持力度不断加大。科学技术是第一生产力，全方位提升科技创新的各个流程对于我国科技兴国的战略具有重要意义。随着科技产业的规范化，科技项目、成果的转化效率受到了更多的重视。与基础研究不同，一个科技成果只有创造出社会和经济效益才有更大的研究价值。因此需要将科技成果的转移预测进行前置，在科技项目立项前就进行完备的可行性评估，保证科技项目的实用价值[1-6]。据统计，我国每年均会产生大量的科技论文、科学专利。然而与发达国家相比，我国的专利转化率仅有10%，远低于欧美发达国家50%-60%。大量的科技成果仅仅停留在理论研究阶段，严重脱离社会生产实际，因此迫切需要提高科技成果的转化效率[7-13]。

综合以上分析，本文结合科技成果转移的流程与当前的科技产业发展背景，提取了影响科技成果转移效率的相关影响变量。基于自组织神经网络构建科技成果转移效率的预测模型，然后搜集主流的科技行业实际科技项目相关数据进行模型的效果仿真[14-16]。

1 理论基础

1.1 自组织神经网络

对于传统的神经网络，其神经元及隐藏层的数目均是固定的，训练过程中只会改变模型前向传播的权重和偏置；此外，传统的神经网络对于高特征维度的训练任务适应性较差，会因为输入特征维度的增长造成网络结构复杂化以及网络的过拟合。因此对于高维数据的输入需要首先完成到低维空间的映射，以降低网络的复杂度。自组织神经网络(SOM)既可以保留样本之间的拓扑映射，又能够降低输入特征空间的维度，其内部连接如图1所示。

图1 自组织神经网络结构

图1给出了一个二维输入，3×3输出的自组织神经网络。在SOM网络中，其关键步骤包含2步：首先是数据信号沿着神经元和神经的正向传播。通过正向传播，网络得到当前输入样本下的输出值；其次是误差的反向传播，每一次的正向传播后，网络会比对实际输出与期望输出，将误差反馈至神经元和神经，进行传播参数的调整。因此，SOM网络训练的关键在于传播参数的调整策略的获取。

对于d维数据，当SOM网络的输出维含有M=m×m个神经元，则每个维度的数据均要对应一个权重向量。此时，权重向量的维度也为d，M则可表示为式(1)。

W={wi|wi∈Rd,i=1,…,M}

(1)

SOM网络经过多次迭代进行网络的训练，每一次迭代均包含竞争、合作2个过程。通过竞争找到最佳匹配单元为式(2)。

(2)

其中，x(t)代表第t次迭代的输入。竞争完成后，对最佳匹配单元和邻域的神经元权重进行调整，实现网络的自组织为式(3)。

wi(t+1)=wi(t)+hci(t)[x(t)-wi(t)]

(3)

式中，用hci(t)定义该神经元邻域内用于保存拓扑关系的更新机制。对于二维网格，其邻域范围如图2所示。

图2 二维网格的合作示意图

图中，圆形区域内的神经元即为最佳神经元的合作神经元。本文的更新机制采用的是高斯函数，即式(4)。

(4)

自组织网络在训练过程中不断调整每个节点连接的权值，从而筛选出更多的获胜神经元。并通过合作保持获胜神经元在与邻域内其他神经元的联系，从而保证网络的拓扑结构稳定。

1.2 SOM误差反向传播训练

自组织神经网络通常采用1.1中所述的自适应过程进行网络的训练。这一训练过程具有较好的抗干扰性和输出结果的稳定性，但计算复杂度较高，模型的输出结果在输入模式较少时与输入样本的输入顺序相关性较高。因此为了获得网络参数的最优调整策略，本文引入了误差的反向传播算法，辅助网络的训练。对于神经网络，其输出层的输出可记为式(5)。

ok=f(netk),k=1,2,3,…,l

(5)

其中,netk为式(6)。

(6)

在神经网络的隐藏层为式(7)。

yj=f(netj),j=1,2,…,m

(7)

其中,netj为式(8)。

(8)

在误差反向传播时，对于输入向量[x1,x2,x3,…,xp]，结合其训练样本存在理想的输入目标向量[d1,d2,d3,…,dp]。在网络的正向传播下，网络存在输出值(xp，yp)。此时，可以得到网络的实际输出和训练样本的理想输出均方差为式(9)。

(9)

对于网络的每一个训练样本，计算其均方差，可得到整个网络的总误差为式(10)。

(10)

根据梯度下降准则，对于权值向量ωsp则有式(11)。

(11)

根据误差的反向传播，在输出层和隐藏层对权值进行修正，记t为模型训练的迭代次数，则输出层为式(12)。

(12)

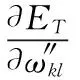
(13)

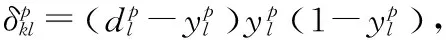
(14)

同理，可得到隐藏层的权重调整计算式为式(15)。

(15)

(16)

(17)

2 方法实现

2.1 评价指标体系构建

科技项目是高新技术企业的核心生产力，提前评估科技成果的转移效率对于高新企业进行项目前期投入与后期融资具有重要意义。为了合理评估科技项目的转移效率，需要构建合理的评价体系。本文从我国风险投资的发展现状出发，结合科技项目评估的前期、中期、后期及跟踪评价4个流程。从科技成果项目本身、承担科技成果项目的企业能力、科技项目的经济可行性和成果项目管理团队4个角度，建立了预测评价体系如图3所示。

(a)

根据图3可知，在使用自组织神经网络进行成果的转移预测时，采用分级的指标体系，共包括4个一级指标和14个二级指标。在划分一级指标时，从科技项目的风险、项目承担企业的经营绩效、项目经济可行性、项目管理团队水平4个角度出发；在划分二级指标时共包含R0-R3、Q0-Q2、W0-W3、T0-T2等14个输入特征。

结合这些输入特征，本文进行模型训练和测试样本的搜集。文中获取、统计2013—2019年之间航空、生物、计算机、芯片、电子、通信6个行业75家企业的724个科技成果从立项到发布过程中的各项投入及获利情况，并对这些企业的生产经营状况与承担科技项目运营的团队进行统计，将这些数据作为模型训练和测试的样本集。

2.2 仿真环境设计

基于以上的数据集和模型，对算法的仿真环境与模型参数进行设计。由于本文在模型仿真时涉及的数据集规模较小，对于计算机硬件的水平要求较低。文中使用的模型仿真环境如表1所示。

表1 算法仿真环境

对于自组织神经网络需要结合模型的训练数据集的规模、输入的特征数、输出结果合理设置模型的参数。其中，最重要的参数包括权值的调整策略、学习率、邻域函数等。网络的建立包括排序和收敛两个阶段，通常将前1 000次训练作为排序阶段。经过排序阶段将神经元之间的连接权值置为有序；然后在收敛阶段降低模型的学习率，直至接近于0，以保证模型的训练误差稳定在可接受的范围内。结合自组织网络的训练特性以及本文模型的应用场景，文中模型的训练参数设置如表2所示。

表2 自组织网络参数设置

2.3 算法仿真结果

本文以科技成果转化后的实际社会收益作为评估模型的预测效率输出结果，以模型的预测误差作为模型性能的评价指标。为了对比不同模型间的性能，本文实验部分的仿真环境采用机器学习算法中经典的训练样本和测试样本以2.5∶1的比例来划分数据集。在仿真过程中，使用全部样本中524个项目作为模型的训练样本，使用剩余200个项目作为模型的测试样本。

为了更优的评估算法的性能，本文选择当前科技成果评估中常用的模糊分析算法作为对比评价算法。模糊分析算法与文中算法在不同行业中对于科技成果预测的误差如表3所示。

从表3可以看出，本文算法在预测误差上较模糊分析法有较大程度的优化。科技项目的平均相对误差来看，模糊分析法的平均误差为13.72%，文中算法误差为7.31%，降低了6.41%。从行业类别来看，两个算法对于航空业的预测精度最高，对于计算机、芯片行业预测精度较低。从行业发展的角度看，航空业虽为高科技行业，但行业发展较为成熟、科技成果的评价体系较为完善。科技成果多为政府大型企业直接参与，本身就有较高的成果转换率，因此具有更高的预测精度；而计算机、芯片行业是朝阳产业，其科技产品创新性较强，需要更多的时间接受市场的检验。

表3 算法误差统计(按行业)

为了评估科技成果转移效率随着时间的变化情况，本文将训练、测试样本按照成果转移的年份进行了统计，统计结果如表4和图4所示。

表4 算法误差统计(按年份)

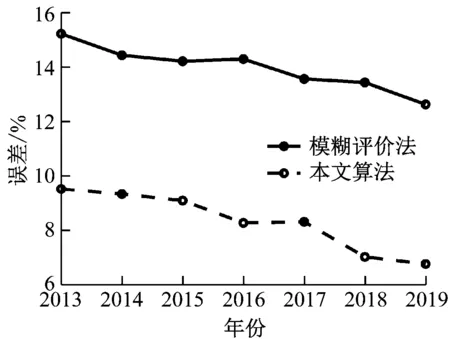
图4 算法误差随年份变化

从表4和图4可以看出，本文算法在按年份统计时，误差也优于模糊评价法。从年份的变化来看，科技项目的转化成果预测精度逐年降低。这说明随着科技项目的投入增大，整个科技行业更加重视对于科技项目的调研、风险评估，这意味着整个高科技产业在向好的方向发展。

3 总结

科技成果的转移是科技项目落地、产生社会价值的重要一环，本文从科技成果项目本身、承担科技成果项目的企业能力、科技项目的经济可行性和成果项目管理团队管理水平等多个角度建立了科技成果的评估体系，基于自组织神经网络对科技成果的转移效率进行预测。从预测精度看，文中的预测值较现有的模糊评价算法有明显的提升，可以为科技项目提供可靠、有效的可行性评估。