基于径向基函数的1∶5万规则分布重力数据插值参数优选
许海红,韩小锋,袁炳强,张春灌,王宝文,赵飞,段瑞锋
(1.中国地质调查局 西安地质调查中心,陕西 西安 710054;2.北方古生界油气地质重点实验室中心,陕西 西安 710054;3.西安石油大学 地球科学与工程学院,陕西 西安 710065;4.陕西地矿物化探队有限公司,陕西 西安 710043)
0 引言
地球物理场在空间上是连续分布的,由于数据采集技术和工区客观条件的种种限制[1],实际观测结果往往是离散分布的[2],但各种数据处理方法和绘图软件均要求资料为严格规则网格数据,因此必须把离散数据进行网格化[3-4]。网格化处理是从测点所提供的坐标及其场值按某一数学模式,计算出网格节点上的场值[5]。这一问题的实质是要在网格节点(网格节点即是“待求点”)附近选取一定数量的测点(测点即是“实测数据点”)进行插值计算[5],因而,插值方法和参数的选取会直接影响到网格化数据的质量、精度和可信程度[6-7]。
近年来,随着地面重磁勘探工作的广泛应用,多数大比例重磁面积测量使用规则测网采样,且通常都是线距、点距相等或线距是点距的2倍。以1∶5万重力测量为例,线距和点距一般为500 m×250 m或500 m×500 m[8]。因此,研究规则分布重力数据的最优插值参数具有实际意义。
前人通过理论模拟重力资料[9]和实测重力资料[10]对多种插值方法进行了对比,对插值间距的变化与影响进行了讨论,研究认为径向基函数法在规则分布重力数据网格化方面的插值精度最高,是最好的插值方法[9-10]。但是,在插值参数选择方面,前人往往根据软件默认值或经验值进行设置[11-12],对插值参数选定以及插值效果的定量对比分析较少,缺乏对数据插值的细化指导;而且,软件默认值或经验值及其搜索方式并不能获得最佳的结果[13],对这些参数的选择会进一步影响插值精度[14-15]。
本文模拟1∶5万野外实测规则分布采样点,以模型理论异常提取的重力数据为基础,采用Surfer软件的径向基函数法进行插值参数优选;依据检查点法获取的残差统计标准偏差指标对比结果,优选出精度较高的插值参数。通过定量比较克服了软件选择参数的随机性和人为选取的不确定性,在探讨各种参数变化引起插值结果精度变化的基础上,提出插值精度较优的参数组合。本文研究结果可为规则分布重力数据的插值工作提供定量依据和参考借鉴。
1 插值参数与精度评价
1.1 主要插值参数
插值参数是构成插值算法的基本元素[16],包括搜索规则和插值核函数(或称基函数)。Surfer软件中径向基函数插值法使用5种核函数[16-17],分别是:反多重二次曲面函数(inverse multiquadric function,IMQF)、多重对数函数(multilog function,MLF)、多重二次曲面函数(multiquadric function,MQF)、自然三次样条函数(natural cubic spline function,NCSF)、薄板样条函数(thin plate spline function,TPSF),其他主要涉及的参数还有:插值间距、插值范围、R2参数(平滑因子)、搜索邻域的形状,搜索半径、搜索角度、搜索扇区、搜索点数等。
1.2 插值精度评价
数据插值效果是否符合实际,需要采用一定的方法评价数据插值方法的合理性和有效性。本文采用检查点法进行插值效果对比,采用Surfer软件中的残差功能,以标准偏差(standard deviation, SD)指标的统计结果来定量分析插值精度并优选插值参数,见式(1)。
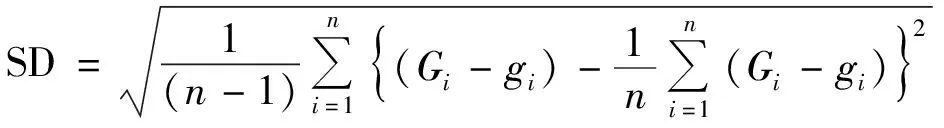
(1)
式中:Gi为第i个数据点(即测点)的实测重力值;gi为第i个数据点(即测点)插值后的重力值;i:1,2,3,…,n;n为数据点的个数。
2 数据来源与插值准备
2.1 数据来源及说明
本次采用RGIS软件设计了由8个异常体组成的地质模型(表1,图1,模型范围17 km×17 km),以该模型的正演重力异常为基础,在异常区内,根据 1∶5万野外工作点线布设原则,模拟部署了点距250 m和线距500 m的工作区(工区范围12 km×12 km),设计测线方向为328°(总体测线方向与异常走向垂直),部署测线25条,每条测线49个测点,合计测点1225个(图1)。采用这1 225个测点为模拟“实测点”,从理论异常中提取出各个“实测点”的重力值作为“实测值”,以此“实测值”为基础进行插值,待插值完成后,使用这1 225个“实测点”作为检查点进行残差分析,统计残差结果获得的标准偏差指标,根据标准偏差值定量比较不同参数对应结果的插值精度。

图1 地质模型(a)及其理论重力异常(b)

表1 理论模型参数
2.2 插值间距与插值范围
插值间距(或称网格间距)是网格化时重要的参数[18],它关系到所派生数据的密度,并影响等值线模型的精度,若网格过大,会丢失一些特征信息,也可能造成等值线扭曲,但是,过细的网格会产生更多冗余的“游离”数据,可能导致网格化时出现“虚假”的现象,实际中,当网格达到一定的间隔后,无论再怎样增加网格数,等值线图的轮廓几乎不再发生任何变化[18]。根据已有研究成果[10],本次插值间距选择0.2 km×0.2 km。
插值范围(或称网格范围)是指网格节点的最大最小坐标范围,也就是等值线的分布范围[18]。一般在插值时默认的插值范围是实测数据点的分布范围(本次“实测点”横向和纵向坐标范围均为0.232 2~16.767 8 km),而实际插值时往往会选择比实测点分布范围更大的网格范围,本次为了便于研究,将插值范围统一设定为0~17 km,由于“实测点”数据测线有一定角度,插值采用方域进行,成图后再利用工区边界“裁剪”外部区域获得“实测点”工区的插值结果[11,19]。
3 插值核函数与R2参数
3.1 五种核函数对比
分别采用径向基函数所属的5种核函数(IMQF、MLF、MQF、NCSF、TPSF)为变量进行插值,其余插值参数统一设置为系统默认值,其中,R2参数为0.018;各向异性中:比率为1,角度为0°;搜索的扇区数为4,从所有扇区使用的最大的数据个数为64,从每个扇区使用的最大的数据个数为16,所有扇区的最小数据个数(更少则白化节点)为8,如果空白扇区多于3个则白化节点;搜索椭圆中,半径R1为11.7,半径R2为11.7,角度为0°。插值结束后采用残差统计结果的标准偏差指标来分析不同核函数的插值效果。
根据检查点法残差指标统计结果可见(图2),自然三次样条函数、薄板样条函数、多重二次曲面函数这3种核函数的插值精度均较高,而多重对数函数插值精度相对较低,反多重二次曲面函数的插值精度最低。因此,对5种核函数插值精度的评级顺序为:自然三次样条函数>薄板样条函数>多重二次曲面函数>多重对数函数>反多重二次曲面函数。通过标准偏差结果的定量对比,认为自然三次样条函数插值精度最高,因而本次优选的核函数为自然三次样条函数。
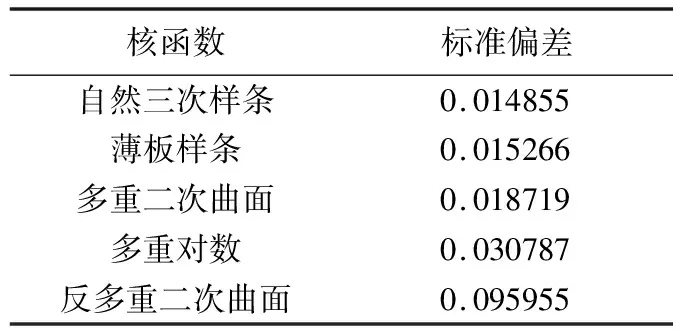
图2 五种核函数残差结果与曲线
3.2 R2参数对比
R2参数是一个平滑因子,也是影响插值精度的一个重要因素[15,17,20],为了比较R2参数变化引起的插值效果变化情况,本次参考系统默认值(0.018)将R2参数设置为0、0.1、0.2等38个变量进行分析,插值过程中,插值核函数为自然三次样条函数,其余插值参数设置为系统默认值(与3.1系统默认值相同),残差统计结果见表2、图3。
由残差指标统计结果可见(表2、图3),随着R2参数的逐渐增大,标准偏差指标值整体是逐渐增大的,根据R2参数对应指标的变化情况可进一步分为4个区间比较:① 第一区间,当R2介于0~1之间时,标准偏差值先减小后增大,且指标值及其变化范围均较小;② 第二区间,当R2介于1~10之间时,标准偏差值也是先减小后增大,但该区域指标值总体变大且变化范围明显增大;③ 第三区间,当R2介于10~100之间时,标准偏差值整体比第二区间增大了2倍多,且随着R2的增加指标值逐渐增大;④ 第四区间,当R2介于100~1 000之间时,标准偏差指标整体抬高且逐渐增大,该区指标值比第三区间增大了3倍多。
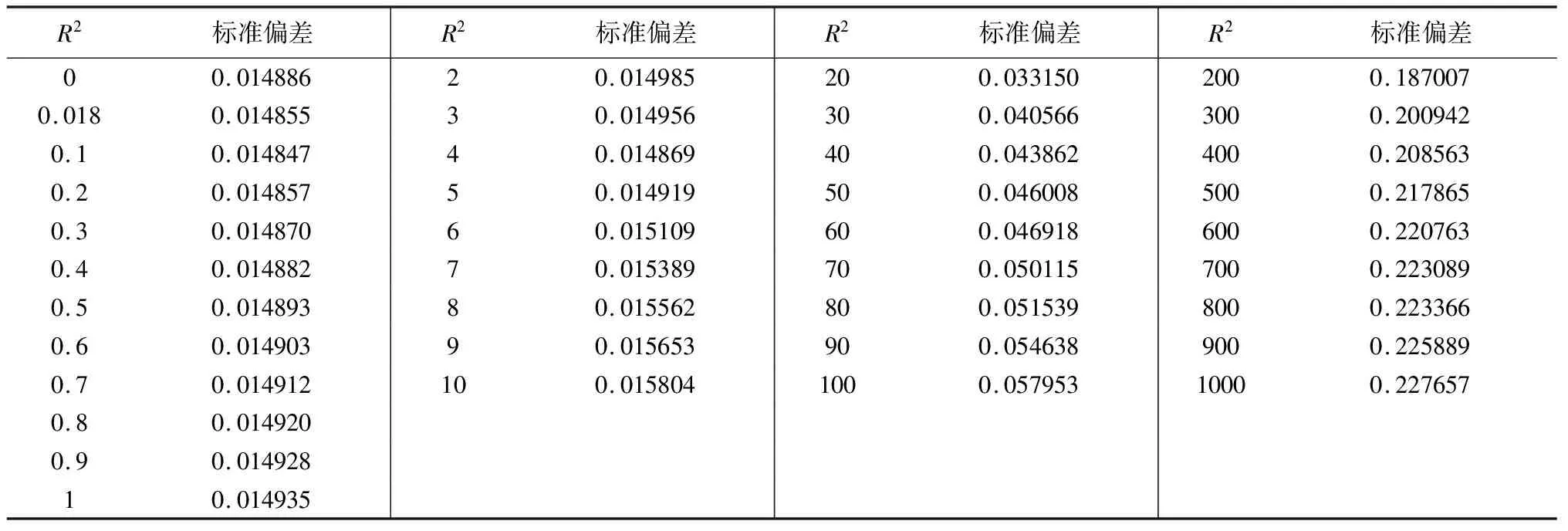
表2 R2参数残差结果
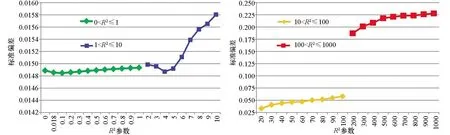
图3 R2参数(平滑因子)残差曲线
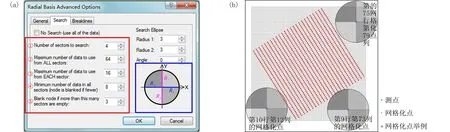
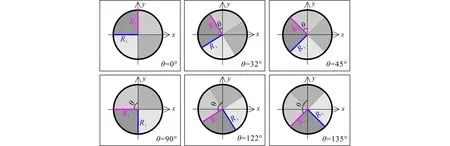
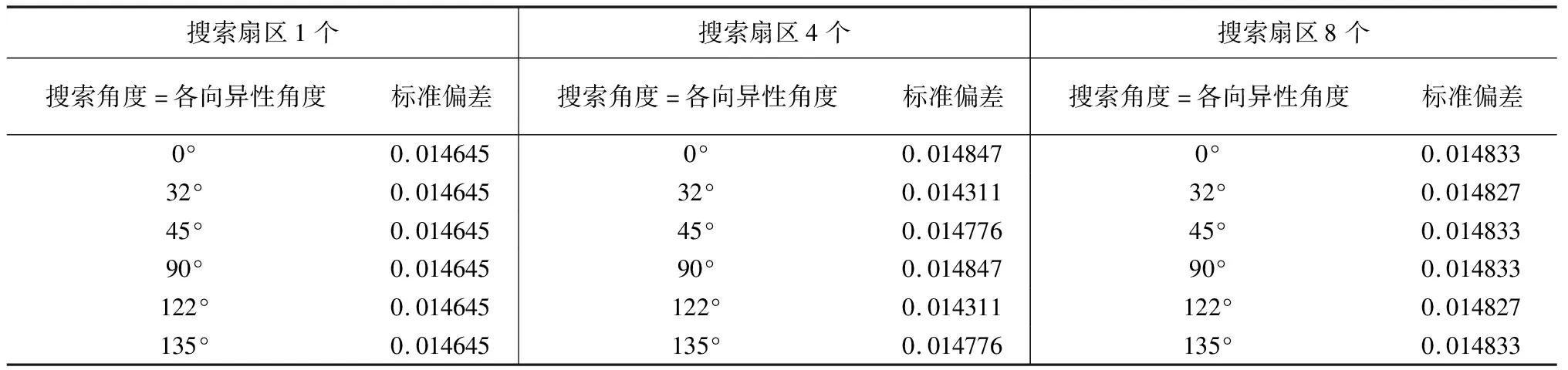
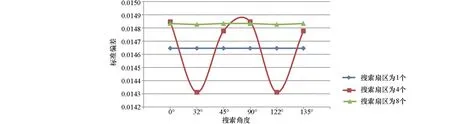
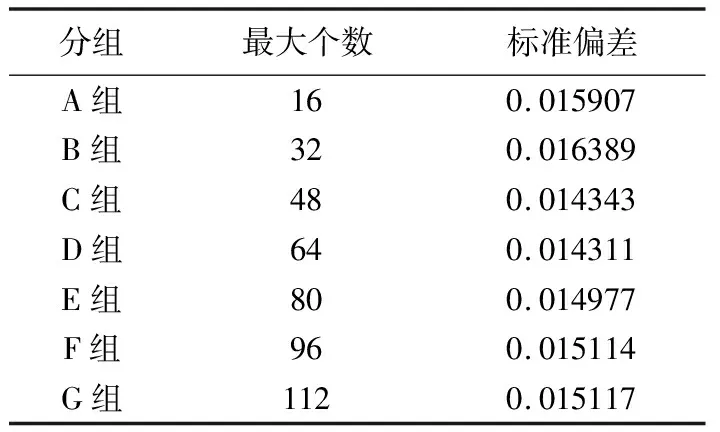
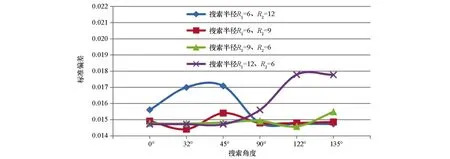
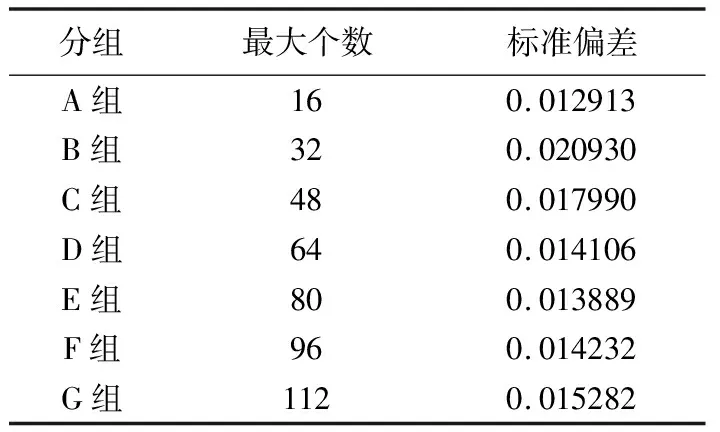
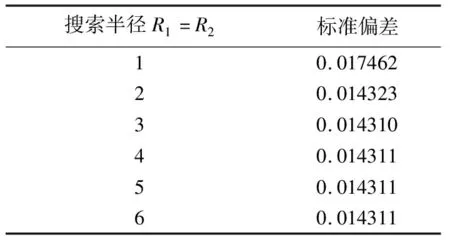
由R2参数标准偏差值的结果可见,当R2参数较大时(10 根据白世彪等[17]的研究,R2参数的一个合理试验值是在平均样本间隔和平均样本间隔的一半之间,本次数据相邻样本(实测点)间隔为0.25 km或0.5 km(图1),平均样本间隔约为0.375 km,据此,R2参数在0.1875~0.375之间(位于本次讨论的第一区间)较为合适。综合考量R2参数的选取原则,结合本次试验标准偏差指标的变化情况,研究认为R2参数不能太大也不宜太小,当R2位于第一区间时插值结果较稳定,根据定量对比结果,本次插值选择R2参数为0.1。 在利用已知点对一个未知点的预测值进行插值计算的过程中,需要指定一个搜索邻域来限制参与计算的已知点的数量和结构。对同一个未知点来说,随着搜索邻域的形状或方向不同,搜索区域内包含的参与计算的已知点的数量和位置也会不同[17]。为了讨论邻域形状及相关参数对插值结果的影响情况,本次设置搜索邻域的形状为圆形和椭圆形分别进行研究,在此基础上对搜索半径,搜索扇区的个数,搜索角度,从所有扇区使用的最大数据个数等参数进行插值讨论并优选。 4.1.1 圆形邻域的搜索半径 通过设置搜索半径R1和R2的大小来调整搜索邻域的形状,搜索半径不能太大也不能太小[11],当搜索邻域为圆形时,设置搜索半径R1=R2,本次参考系统默认值(11.7 km),分别取搜索半径为6、8、10、14、16 km这5种大小进行对比,插值过程中,插值核函数为自然三次样条函数,R2参数为0.1,其余插值参数设置为系统默认值(与3.1系统默认值相同)。 由残差指标统计结果表3可见,当搜索半径R1=R2且介于6~16 km之间时,其标准偏差值未发生变化,可见搜索半径选择6~16 km之间均可,根据王玉敏等的研究可知,在搜索规则不变的条件下,任意改变搜索半径的大小,对数值点区域的等值线不产生影响[11],本次考虑到搜索半径不能太小,因而初步设置搜索半径为6 km进行插值参数优选。 表3 圆形邻域搜索半径残差结果 4.1.2 圆形邻域的搜索扇区与搜索角度 搜索扇区也称搜索分区(或称搜索方向),当搜索半径不变时,搜索扇区及搜索角度会影响到插值精度,参考白世彪等[17]、杜红悦等[14]、张锦明等[15-16]、王玉敏等[11]等的研究,本次设置搜索扇区数为1个、4个、8个等3种情况进行比较,其余搜索参数设置的对应情况见表4。 由表4可见,搜索扇区设置主要涉及5个参数(图4a中红色线框内):第①个参数为搜索扇区个数,即指将搜索区域划分为几个扇区;此处以4个扇区为例(图4a中蓝色线框内)对表4中相关参数进行说明,同时,设置搜索邻域为圆形(Radius1=Radius2),搜索半径R1=R2=3 km,搜索角度(Angle)为0°。第②个参数为从所有扇区使用的最大的数据个数,即指在所有扇区内参与插值的最大数据个数。第③个参数为从每个扇区使用的最大的数据个数,即指在每个扇区内参与插值的最大数据个数。第④个参数为所有扇区的最小数据个数(更少则白化节点),由图4(b)可见,对于第10行第12列的网格化点而言,在所有搜索扇区内共有9个测点(大于8个),因此该网格化点插值后可以得到一个网格值,但是对于第9行第73列的网格化点而言,在所有搜索扇区内共有4个测点(小于8个),因此该网格化点被白化,插值后没有网格值(意指更少则白化节点)。第⑤个参数为如果空白扇区多于此数则白化节点,由图4(b)可见,对于第75行第79列的网格化点而言,所有扇区内没有测点,4个扇区均为空白扇区(空白扇区大于3个),此时该网格化点被白化,插值后没有网格值。 表4 搜索扇区及对应搜索点数 图4 搜索界面选项(a)与搜索点分布图示(b) 为了同时比较搜索角度(本文设置搜索角度Angle为搜索半径R2与Y轴的夹角)对插值精度的影响,本次设置搜索角度为0°、32°(搜索半径R2平行测线)、45°、90°、122°(搜索半径R2垂直测线),135°这6个方向(图5)。 图5 不同搜索角度图示 插值过程中,插值核函数为自然三次样条函数,R2参数为0.1,搜索半径R1=R2=6 km。根据白世彪等的研究认为设置搜索椭圆主半轴与次半轴的比和角度与各向异性比和角度相一致时,可得到较满意的结果[17],因而本次设置各向异性比率=搜索半径R1与R2之比=6/6=1,各向异性角度=搜索角度,残差统计对比结果见表5、图6。 由表5、图6可见,采用不同搜索扇区插值时,获得的插值精度有所不同:搜索扇区为1个时,标准偏差值无变化;搜索扇区为4个时,标准偏差值变化较大,与搜索扇区为1个时的残差结果相比插值精度有高有低;搜索扇区为8个时,标准偏差值变化较小,且总体比搜索扇区为1个时的残差结果大。进一步分析发现,不同搜索扇区中,搜索角度的变化对插值结果也有不同的影响:当搜索扇区为1个时,插值精度不会随着搜索角度的变化而变化;当搜索扇区为4个时,不同搜索角度的插值结果精度大小为:32°=122°>45°=135°>0°=90°;当搜索扇区为8个时,不同搜索角度的插值结果精度大小为:32°=122°>0°=45°=90°=135°。 表5 圆形邻域不同搜索扇区对应残差结果 图6 圆形邻域不同搜索扇区残差曲线 综合考虑搜索扇区与搜索角度对插值结果的影响可见,搜索扇区为4个时,搜索半径R2与测线平行(或垂直)时,残差分析获得的标准偏差值最小、插值精度最高,因此,搜索扇区选为4个,搜索角度选为搜索半径R2与测线平行(或垂直)时的角度插值效果最好。 4.1.3 圆形邻域时从所有扇区使用的最大的数据个数 对同一个网格节点(即“待求点”)而言,在插值过程中,当搜索半径、搜索扇区、搜索角度不变时,搜索邻域内参与插值的测点(即“实测点”)数量对网格节点的待求值也有一定的影响,本次设置了7组参数进行对比(表6)。插值过程中,插值核函数为自然三次样条函数,R2参数为0.1;搜索扇区个数为4个,搜索半径R1=R2=6 km,搜索角度为32°(或122°,即搜索半径R2与测线平行或垂直时的角度),各向异性比率为1,各向异性角度为32°(或122°与搜索角度相同),其他参数见表6,插值结果见图7。 表6 圆形邻域扇区为4个时最大数据个数 由图7可见,随着从所有扇区使用的最大的数据个数不断增大,其对应的标准偏差指标值先增大再变小后又变大;作图发现当最大数据个数为16时,实测点的4个角点附近插值结果为空白区,因此最大个数为16时不能满足插值需求。由图7可见,最大数据个数≤32个点时,标准偏差值偏大,最大数据个数≥80个点时,标准偏差值相对较小,当最大数据个数介于48~64之间时,标准偏差值最小;由此可见,搜索的最大数据点个数较少时插值误差大,数据个数增多后插值误差相对减小,但数据点并非越多越好,对比标准偏差指标,本次选择从所有扇区使用的最大的数据个数为64个,能够获得较高的插值精度。 图7 圆形邻域扇区为4个时最大数据个数残差结果与曲线 4.2.1 椭圆形邻域的搜索半径与扇区和角度 当搜索邻域的形状为椭圆形时,综合考虑搜索半径、搜索扇区和搜索角度的影响,同时设置相关参数进行对比。参考圆形邻域搜索半径试验情况,设置椭圆形邻域的搜索半径R1和R2为4类组合进行插值比较,其中,A类:R1=6,R2=12;B类:R1=6,R2=9;C类:R1=9,R2=6;D类:R1=12,R2=6。设置搜索扇区分别为1个、4个、8个,各扇区对应的搜索点数设置与表4中参数相同。设置搜索角度为0°、32°、45°、90°、122°、135°这6个方向,其余参数设置:插值核函数为自然三次样条函数,R2参数为0.1,各向异性比率=搜索半径R1与R2之比,各向异性角度=搜索角度,插值残差统计结果见表7~表9。 表7 椭圆形邻域扇区为1个时不同参数对应的残差结果 表8 椭圆形邻域扇区为4个时不同参数对应的残差结果 表9 椭圆形邻域扇区为8个时不同参数对应的残差结果 由表7、表8、表9的残差指标值和图8、图9、图10的曲线对比可见,搜索半径R1/R2=0.5和R1/R2=2时,不同搜索角度插值获得的标准偏差值变化范围均较大,而搜索半径R1/R2=0.667和R1/R2=1.5时,不同搜索角度插值获得的标准偏差值变化范围均较小。 图8 椭圆形邻域扇区为1个时残差曲线 图9 椭圆形邻域扇区为4个时残差指标曲线 图10 椭圆形邻域扇区为8个时残差指标曲线 当搜索扇区固定时,不同搜索半径对应的插值结果变化趋势较为相似:① 当搜索半径R1/R2=6/12时,较大的搜索角度(90°~135°)插值得到的标准偏差值相对较小,而较小的搜索角度(0°~45°)插值得到的标准偏差值相对较大;② 当搜索半径R1/R2=12/6时,较小的搜索角度(0°~45°)插值得到的标准偏差值相对较小,而较大的搜索角度(90°~135°)插值得到的标准偏差值相对较大;③ 当搜索半径R1/R2=6/9时,较大的搜索角度(90°~135°)插值得到的标准偏差值相对集中,而较小的搜索角度(0°~45°)插值得到的标准偏差值同时出现了最小和最大值;④ 当搜索半径R1/R2=9/6时,较小的搜索角度(0°~45°)插值得到的标准偏差值相对集中,而较大的搜索角度(90°~135°)插值得到的标准偏差值同时出现了最小和最大值。 由表7与表5对比可见,当搜索扇区为1个时,搜索半径不等的情况下任何一组参数插值后的标准偏差指标均大于搜索半径相等时的插值结果。由表8与表9对比可见,搜索扇区为4个或8个时,搜索半径与搜索角度变化时所对应的插值结果标准偏差值变化特征相似,其中,标准偏差的最小值均出现在搜索半径R1/R2=6/9且搜索角度为32°时,且均比圆形邻域(表5)中对应的标准偏差值更小。对比表7、表8和表9的各项标准偏差值变化情况,综合分析认为,椭圆形邻域时,选择搜索扇区为4个,搜索半径R1/R2=6/9,搜索角度为32°时,插值结果对应的标准偏差值更小,插值精度更高。 4.2.2 椭圆形邻域时从所有扇区使用的最大的数据个数 参考圆形邻域时搜索点数设置情况(表6),在椭圆形邻域对搜索点数的对比中也同样设置7组参数进行分析,插值过程中,插值核函数为自然三次样条函数,R2参数为0.1;搜索扇区为4个,搜索半径R1=6、R2=9,搜索角度为32°,各向异性比率为 0.667,各向异性角度为32°,插值结果残差见图11。 由残差结果(图11)可见,随着最大数据个数的不断增大,椭圆形邻域标准偏差指标变化趋势与圆形邻域时最大数据个数残差结果的变化趋势相似;而且最大点数为16时实测点最外侧工区的4个拐点附近插值结果也为空白区,不能满足插值需求。根据图11的对比结果,当最大数据个数为80时,标准偏差值最小,因此选择从所有扇区使用的最大的数据个数为80个,插值精度最高。 图11 椭圆形邻域扇区为4个时最大数据个数残差指标结果与曲线 根据不同形状搜索邻域初步设置的搜索半径为基础,通过对搜索扇区、搜索角度、搜索点数的比较,优选了各个插值参数相应的最佳取值范围;反之,当这些搜索参数均有明确的定量化取值与条件限制时,搜索半径的大小能否更加优化进一步提高插值效率?下面针对搜索半径相等与不等两种情况进行讨论。 当搜索邻域为圆形时,搜索半径R1与R2相等,设置搜索半径R1=R2并分别为1、2、3、4、5 km等5种情况进行对比,插值核函数为自然三次样条函数,R2参数为0.1,其他参数依据圆形邻域比较的最优指标设置为:搜索扇区个数为4个,搜索角度为32°,各向异性比率为1,各向异性角度为32°,从所有扇区使用的最大的数据个数为64,从每个扇区使用的最大的数据个数为16,所有扇区的最小数据个数(更少则白化节点)为8,如果空白扇区多于3个则白化节点。 由残差统计结果(图12)可见,随着搜索半径的增加,残差指标值先减小后增大,当半径为3 km时标准偏差取得最小值。根据相邻相似的原则,随着实测点与预测点之间距离的增加,实测点的值与预测点的值之间的相关性也随之降低[17],在一定距离之外,实测点对预测点的影响很小。对同一个预测点来说,当搜索半径超过某个距离范围后,随着搜索半径的增大,插值精度基本不变。 图12 搜索半径R1与R2相等时残差结果与曲线 另外,对于周围“实测点”数量较少的边界点而言,以边界测线的拐角“预测点”(网格化节点)为例(见图1中蓝色线框),当搜索半径变化时,其半径内包含的“在所有扇区的最大数据个数”也随之变化(图13),搜索半径为1 km时最大数据约8个、搜索半径为2 km时最大数据约29个、搜索半径为 3 km时最大数据约63个、搜索半径为4 km时最大数据约109个(远大于4.1.3中优选的64个点)。由此可见,搜索半径小于3 km时其搜索范围内的数据点个数太少,不能满足插值需求;当搜索半径大于3 km时,搜索数据点个数能够满足插值需求,但是由于距离较大,一定距离范围之外实测点对预测点的影响比较小,对插值结果的贡献不大。综合对比认为,当搜索半径R1与R2相等时,搜索半径设置为3 km即能够得到较高的插值精度、获得较好的插值结果。 图13 搜索半径R1与R2相等时插值点分布图示(网格化节点范围见图1蓝色线框) 当搜索邻域为椭圆形时,搜索半径R1与R2不等,根据椭圆形邻域不同半径对比结果,当搜索半径R1/R2=6/9=0.667,且搜索扇区为4个,搜索角度为32°,获得的插值精度更高。因此,分别设置搜索半径R1=1 km、R2=1.5 km,R1=2 km、R2=3 km,R1=3 km、R2=4.5 km,R1=4 km、R2=6 km,R1=5 km、R2=7.5 km,R1=6 km、R2=9 km等6组情况进行比较,插值核函数为自然三次样条函数,R2参数为0.1,其他参数依据椭圆形邻域研究的最优指标设置为:搜索扇区个数为4个,搜索角度为32°,各向异性比率为0.667,各向异性角度为32°,从所有扇区使用的最大的数据个数为80,从每个扇区使用的最大的数据个数为20,所有扇区的最小数据个数(更少则白化节点)为8,如果空白扇区多于3个则白化节点。 由残差统计结果(图14)可见,随着搜索半径的增加,残差指标值先减小后增大,这与半径R1、R2相等时的特征相似,即:对同一个预测点来说,在一定距离之外,实测点对预测点的影响很小,随着搜索半径的增大,插值精度基本不变。 图14 搜索半径R1与R2不等时残差结果与曲线 同样,当搜索半径变化时,其半径内包含的“在所有扇区的最大数据个数”也随之变化,以边界测线的拐角预测点为例(见图1中蓝色线框),搜索半径R1/R2为1/1.5时最大数据约12个(图15)、搜索半径R1/R2为2/3时最大数据约43个、搜索半径R1/R2为3/4.5时最大数据约93个(大于4.2.2中优选的80个点)。对比图14残差统计结果可见,当搜索半径R1/R2为1/1.5或2/3时,个别边界测点对应的最大搜索点个数较少(远小于80个),因此其插值结果精度较低,当搜索半径R1/R2为4/6或5/7.5和6/9时,搜索点数均能够满足插值需求,插值精度较高且较稳定,综合对比而言,当搜索半径R1/R2为3/4.5时标准偏差值最小,插值精度最高,因而选择搜索半径R1/R2为3/4.5进行插值可获得较优的插值结果。 图15 搜索半径R1与R2不等时插值点分布图示(网格化节点范围见图1蓝色线框) 由搜索半径R1与R2两种情况优选对比结果可见,当R1与R2不等时(图14)其残差分析的标准偏差比R1与R2相等时(图12)标准偏差指标值小,这说明椭圆形的搜索邻域比圆形的搜索邻域插值精度高,插值结果更接近实测值。参考前人研究可知,重力场实际上是一各向异性场[21],虽然实测数据是均匀采样的,但是实测已知点对数据的权重存在方向性的影响,因而,设置椭圆形搜索邻域(考虑了各向异性)比圆形搜索邻域(没有考虑各向异性)更符合实际。 本文采用理论模型的正演重力异常,模拟部署1∶5万野外实测点并进行插值参数优选,采用检查点法根据残差分析的标准偏差指标大小定量比较插值精度,综合分析插值效果选定了最优插值参数,研究结果对于选取插值参数的大小和范围具有定量化的参考和指导意义,通过本次研究取得以下几点认识: 1)重力异常插值参数会影响插值结果的精度,搜索邻域的形状不同时,其插值参数变化对于提高插值精度的影响程度有所不同,与默认参数的插值结果(图2)相比而言,圆形邻域优选结果(图12)对应的插值精度最大可提高570.55%,最小可提高 3.81%;椭圆形邻域优选结果(图14)对应的插值精度最大可提高590.92%,最小可提高6.96%。 2)5种核函数插值精度高低排序为:自然三次样条函数>薄板样条函数>多重二次曲面函数>多重对数函数>反多重二次曲面函数,其中自然三次样条函数的插值精度最高。 3)R2(平滑因子)参数对应的4个区间插值精度大小为:第一区间>第二区间>第三区间>第四区间,其中第一区间标准偏差指标变化较小、插值精度更趋稳定,本次优选R2参数为0.1。 4)搜索邻域为圆形时,最优插值参数分别为:搜索半径R1=R2=3 km,搜索扇区为4个,搜索角度为32°(或122°,即搜索半径R2与测线平行或垂直时的角度),各向异性比率为1(等于搜索半径R1与R2之比),各向异性角度为32°(或122°与搜索角度一致),从所有扇区使用的最大的数据个数为64个,从每个扇区使用的最大的数据个数为16个,所有扇区的最小数据个数(更少则白化节点)为8个,如果空白扇区多于3个则白化节点。 5)搜索邻域为椭圆形时,最优插值参数分别为:搜索半径R1=3 km、R2=4.5 km,搜索扇区为4个,搜索角度为32°(即搜索半径R2与测线平行时的角度),各向异性比率为0.667(等于搜索半径R1与R2之比),各向异性角度为32°(与搜索角度一致),从所有扇区使用的最大的数据个数为80个,从每个扇区使用的最大的数据个数为20个,所有扇区的最小数据个数(更少则白化节点)为8个,如果空白扇区多于3个则白化节点。 6)重力异常为各向异性异常,建议选用椭圆形邻域进行插值,且主半轴R1小于次半轴R2;在插值过程中应考虑特定方向上的权重值,主半轴R1垂直测线,次半轴R2与测线平行。4 搜索邻域及搜索点数
4.1 搜索邻域为圆形



4.2 搜索邻域为椭圆形





5 搜索半径的优化
5.1 搜索半径R1与R2相等
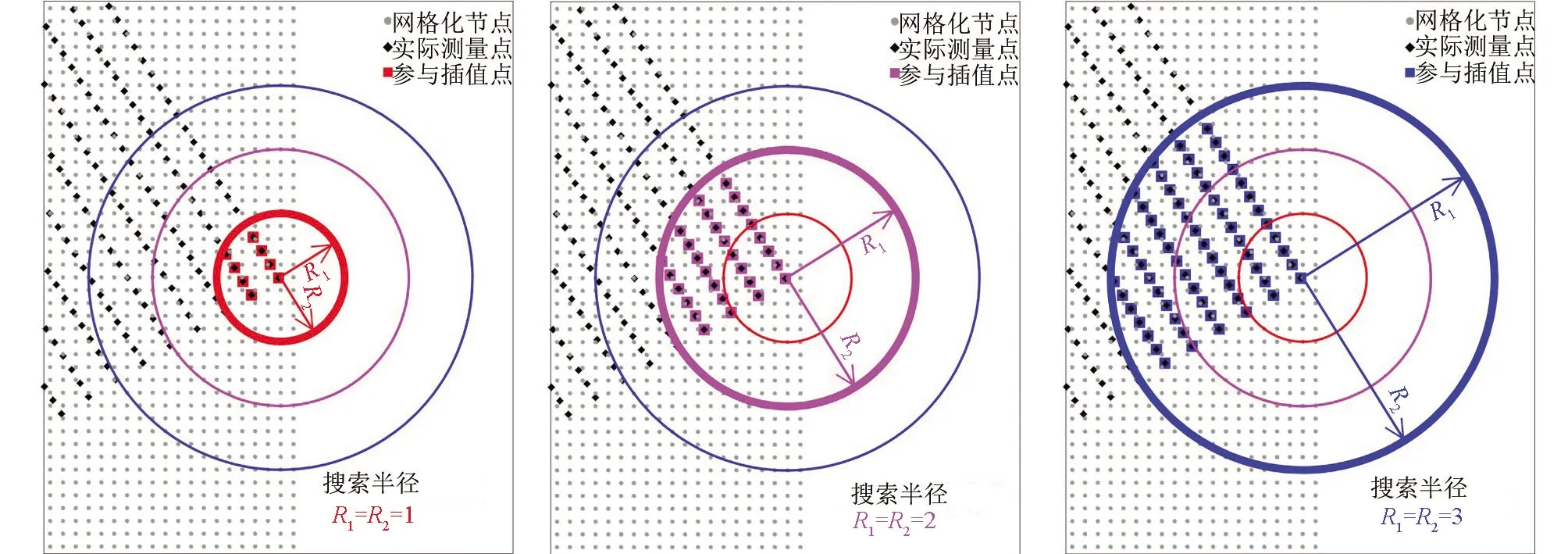
5.2 搜索半径R1与R2不等
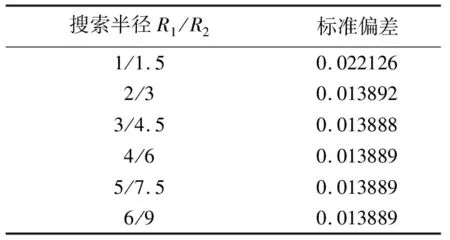
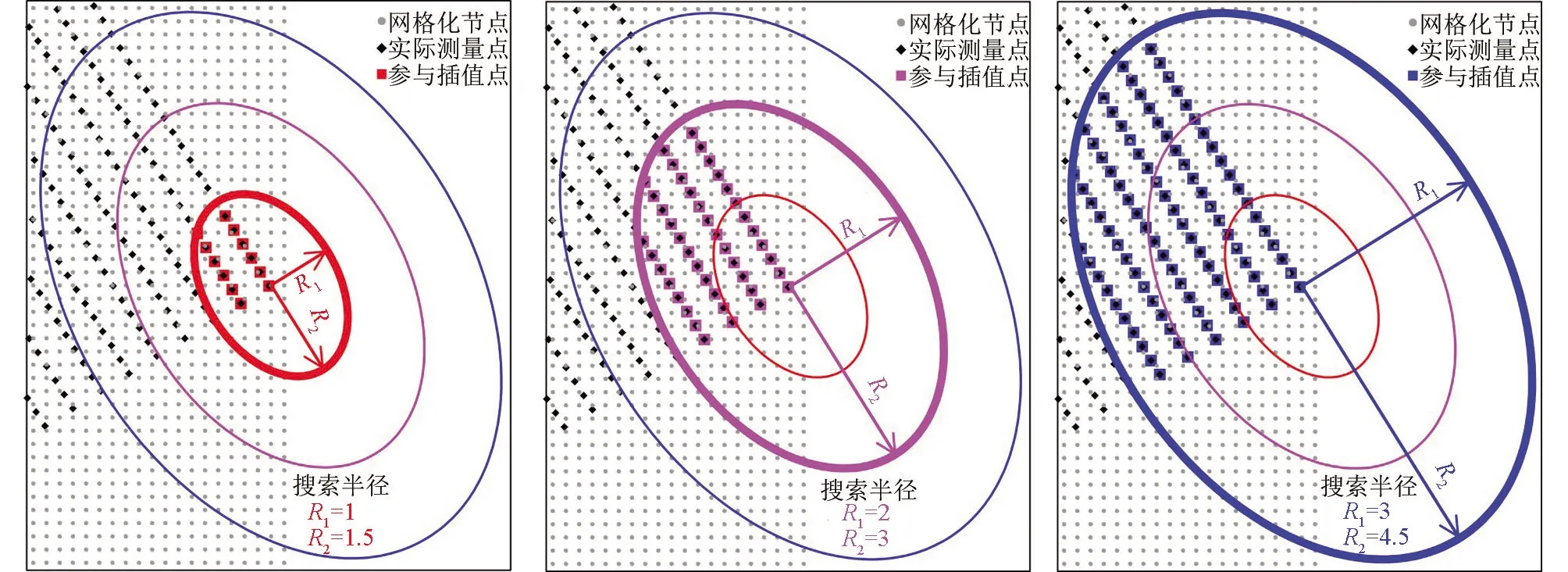
6 结论

