基于测点实测高程修正重力中区地改误差评价方法的探讨
耿涛,杜辉,冯治汉
(1.中国地质调查局 西安地质调查中心,陕西 西安 710054;2.西北地质科技创新中心,陕西 西安 710054)
0 引言
现阶段的重力调查工作中,随着重力仪器精度的不断提高和高精度差分GPS测地技术的广泛使用,重力值观测精度、布格改正精度、正常场改正精度均有大幅度提高,重力地形改正的精度对布格重力异常总精度的影响越来越大,这一点大家已有共识。而在重力地形改正工作中,近区地形改正值一般通过野外实测获得,在不断引入新技术后,近区地形改正的效率和精度都有了极大的提高[1-3];而远区由于距离较远,其地形影响对于一定范围内的重力异常已经可视为常量[4],对布格重力异常形态的影响较小,在研究局部异常特征时影响不大。因此,重力中区地形改正(下文简称中区地改)的精度是影响重力异常精度的关键。
几十年来,众多专家学者和专业技术工作者为提高地形改正精度持续不断地做了大量工作。20世纪80年代以前,主要是进行改正方法方面的研究[5-8],20世纪90年代后期,随着计算机技术的发展,则在计算机算法研究[9-13]、不同算法的对比研究[14]、不同源数字高程模型(digital elevation model,DEM)适用性试验研究[15-17]等方面取得了众多成果,这些成果的应用大大提高了中区地改的精度。然而,中区地改的误差是客观存在的,通过努力可以减小它,但不能消灭它。因此,在重力调查工作中,掌握中区地改误差的实际大小,就显得同样重要,这有助于我们掌握重力异常的实际精度,对后续研究工作中的异常判别、认识、反演、推断、解释都有帮助。误差统计只是手段,真实掌握重力异常的精度才是目的,一个漂亮但不真实的误差统计数据是没有意义的。
具体到一个工作区,中区地改工作完成后,其精度到底能达到多少?这就涉及到中区地改的精度评价问题。
重力地形改正的目的就是要消除由于地形的起伏不平对测点重力观测值的影响。因此,在不考虑地层密度变化的前提下,无论地形改正采用的地形资料(包括地形图和DEM数据)如何获得,越逼近实际地形,地形改正的精度就越高。在实际工作中,所谓对实际地形的逼近包含两个层面:首先是地形资料对实际地形的拟合程度(即地形资料的精度,如图1a所示),其次是在地形改正值计算过程中所采用的算法对地形资料的拟合程度(即计算方法的精度,如图1b所示)。

图1 重力地形改正中存在的两种误差示意
不难理解,任何算法的精度讨论都是建立在所采用地形资料为真值的基础之上的,如果所用地形资料本身对实际地形的描述差异就很大(即地形资料精度很低),那么采用什么样的算法地形改正精度也不可能高。因此,札喜旺登在1983年就指出,在影响重力地形改正精度的7个方面中,对地形改正精度影响最大的是地形图的精度与地形模型单元大小的划分,其他因素都是次要的[18]。
可见,在实际工作中,评价一个工作区中区地改精度时,不能回避所用地形资料精度对重力地形改正精度的影响。前人在方法研究过程中提出的一些精度评价方法,基本上是基于同一种地形资料对精度的评价方法进行研究[19-20],或者是讨论不同算法间的精度差异,或者是对比不同源DEM数据间的精度差异,而没有考虑地形资料本身的精度问题,这在方法研究中无可非议,但把这些精度评价方法直接应用在实际工作中是有问题的,因为这些精度评价方法没有考虑地形资料精度对重力地形改正精度的影响。本文的目的就是探讨通过具有可操作性的方法评价地形资料精度对重力地形改正精度的影响。
1 实际工作中中区地改精度评价常见问题
实际工作中,中区地改的精度评价都是依据各种重力规范中的要求进行的,首先了解一下规范中的精度评价要求。
1.1 规范对中区地改精度评价的要求
表1是目前地矿行业主要执行的3种重力调查技术规范对中区地改精度评价的要求。为了能体现出技术要求的延革,表中列出了规范修订前后的对照。
从表1可以看出,不同比例尺重力规范对中区地改的质量检查要求中,都是考虑到了中区地改所用地形图或DEM的精度问题的,因此,在给出同精度质量检查方法的基础上,建议有条件的地区采用更大比例尺的地形图或DEM重新计算地形改正值,作为高精度检查来评价中区地改精度。因为,一般来说,在同一地区,更大比例尺地形图或DEM测绘精度更高,数据网度更密,描述的地形更逼近实际地形。
但是,规范给出的同精度检查方式,由于采用的地形图或DEM数据没有变,实际上是忽略了地形图或DEM本身的精度问题。
1.2 实际工作中常见问题
从表1可以看出,常用的重力规范中虽然都有建议采用更高精度的地形图或DEM来检查中区地改的精度,但因为这个建议不是强制性的,因此,在一般生产单位的实际工作中,鲜有按此建议进行中区地改精度检查的。

表1 规范对中区地改精度评价的要求
由于没有统一的要求,目前在实际工作中,中区地改的方法多种多样。由于采用计算机计算的中区地改的方法已非常成熟,人工圆域量板读图改正法已被淘汰。在中区地改精度评价时,采用人工圆域量板读图法来检查计算机计算中区地改结果,本身是一种低精度改正结果检查高精度改正结果的方法[18],因此也不再被采用,而主要采用变换高程数据节点位置法或采用不同算法重新计算。
但是,正如前文所述,这些方法都是基于同一种DEM数据进行的,回避了DEM本身的精度问题。对于一些地形相对平缓的工作区或采用的DEM数据节点本身较密的工作区,变换高程数据节点位置法或采用不同算法重新计算,其结果差异是非常小的,这也是经常见到一些项目中区地改质量检查精度畸高的原因。
造成这一现象的原因,笔者认为,并非是大家没有意识到DEM精度对中区地改精度有影响,而是缺少对DEM精度进行评价的手段。规范中给出的建议出发点是好的,但在实际工作中操作性不强。原因如下:
首先,如果按规范的建议进行中区地改精度检查,由于质量检查要求均匀分布的原则,则要求工作单位需准备两套DEM数据,一套符合规范要求的DEM数据进行中区地改工作,另一套精度更高的DEM数据专门用来进行质量检查。由于在同一地区,获取更高精度的DEM数据往往需要花费更高的代价,甚至需要专门测绘、制作。出于项目经费和工作成本考虑,除非是有特别的研究需要,没有哪个单位愿意去准备两套数据。
其次,如规范中建议所言,有条件的地区(可理解为项目承担单位本身就有工作区不同比例尺的两套或以上DEM数据),那么,也不会采用规范中建议的方法进行中区地改精度检查。因为,规范中规定的中区地改所应采用的地形资料比例尺是精度下限,为了提高中区地改精度,在实际工作中一定是采用最高精度的DEM来完成中区地改工作,而不是仅仅用来做精度检查。
因此,如何评价地形DEM的精度,是更真实地评价中区地改精度的重要内容。
2 采用重力测点实测高程值评价DEM精度
2.1 方法的可行性
在当前的重力调查工作中,随着高精度差分GPS测地技术(包括GPS快速静态、GPS-RTK、CORS系统等)的广泛使用,中、小比例尺重力调查工作中,重力测点的三维坐标测量精度已经可以达到分米级,大比例尺重力勘探中重力测点的三维坐标精度甚至可达到厘米级,并且,重力测点是均匀地分布于整个工作区的。
而用于进行中区地改的DEM数据主要是通过航空摄影测量法、航天遥感测量法、地形图扫描矢量化法及数字线划图缩编法等方法生成数字线划图(DLG)[27],在此基础上再生成DEM[28],其精度指标分别按测绘行业标准CH/T9001.1-2013[29]和CH/T9001.2-2010[30]执行。其中DEM的精度指标见表2。

表2 数字高程模型(DEM)精度指标
从表2可见,在实际工作中重力测点三维坐标测量精度是优于DEM精度的,利用重力测点实测高程对中区地改用DEM数据进行检查,相当于对其进行高精度检查,是可行的。
2.2 检查方法
在利用重力测点实测高程对中区地改用DEM数据进行检查前,首先要保证两种数据采用的是相同的坐标系统,如果不是,则应先进行坐标转换。现在按规定均应采用CGCS 2000国家坐标系,1985国家高程基准。
以实测重力测点的平面坐标为准,在DEM上读取相应点的高程;注意高程值的内插方法应与进行中区地改时选用的方法相同。
计算各个重力测点实测高程与DEM高程的差值,采用如下高精度质量检查均方误差统计公式计算DEM的均方误差:
(1)
式中:Δh为重力测点DEM读取高程与实测高程之差;n为重力测点数。
目前在中、小比例尺重力调查工作中,中区地改采用的DEM比例尺一般是1∶10000和1∶50000,因此,计算DEM的均方误差宜用高精度质量检查均方误差统计公式,而对于大比例尺重力勘探工作,如果地形条件较好,DEM的精度较高,应采用如下同精度质量检查均方误差统计公式计算DEM的均方误差:
(2)
式中各项含义同公式(1)。
如果实际工作中中区地改使用了其他来源的高程模型数据,检查时采用何种均方误差统计公式应视所用数据具体情况确定。
3 DEM误差引起的中区地改误差的评价方法探讨
用上述方法评价DEM的精度是符合抽样检查要求的,其结果可视为DEM的均方误差。但是,我们的最终目的是评价中区地改的精度,因此,需要计算DEM的误差引起的中区地改误差。
然而,这是一个困难的问题。因为理论上讲,只有用更高精度的DEM数据才能在更高精度标准上评价中区地改误差,或是用同等精度但不同数据源的DEM数据做同精度的中区地改误差评价。重力点实测高程虽然可以作为抽样点检查DEM高程精度,但要用来检查中区地改的精度,实测高程点的密度(即对实际地形描述的精确度)是远远不够的,因此只能通过别的途径估算DEM的误差造成的中区地改误差。
如图1a所示,DEM的误差包括地形细节描述不准确和地形高程不准确两方面,由地形改正的原理可知,其中地形高程不准确造成的误差是主要的,而地形细节描述不准确造成的误差相对要小很多。因此,可以考虑采用DEM读取高程计算的中区地改值和实测高程计算的中区地改值之差,来近似替代DEM地形与实际地形不一致引起的中区地改误差。
具体方法为,抽取一定比例的重力测点,采用DEM读取高程和重力测点实测高程分别计算中区地改值,并计算其差值,对所有检查点的差值做均方误差统计。由于DEM与实际地形的误差是非线性的,我们可以大致判断实测重力点外围的DEM网格点数据在近处与实际地形拟合情况,但无法判定其在远处与实际地形的拟合程度,因此应采用式(3)的同精度检查公式进行误差统计。
(3)
式中:δi为DEM高程和实测高程分别计算的中区地改值之差;n为检查点数。
关于评价DEM误差引起的中区地改误差的方法,我们在讨论时还提出了两种方案:
一是计算在中区地改范围内、厚度为实测高程与DEM高程差值(hS-hD)的板状模型引起的重力值,减去近区地改值后,近似视为该重力测点由DEM误差引起的中区地改误差,在此基础上统计均方误差。该方案还可进一步减化为利用全区实测高程与DEM高程差值的平均值或是均方误差值为厚度计算板状模型引起的重力值,将计算结果直接作为全区DEM误差引起的中区地改均方误差的近似值。
二是采用在DEM数据上增加噪声的方法模拟计算由DEM误差引起的中区地改误差。方法是生成一组和DEM网格数据一致且满足正态分布的随机数,使其平均数μs和标准离差σs等于实测高程和DEM高程的误差平均数μ和标准离差σ,将该随机数与DEM数据相加(相当于在DEM数据上增加了噪声),得到一个新的DEM数据;用新的DEM数据和原DEM数据分别计算中区地改值,用两次计算结果差值的均方误差模拟全区DEM误差引起的中区地改均方误差。
上述方法哪一种计算结果更接近实际误差,需进行大量的对比实验才能确定,本文先以第一种方法进行探讨。
4 中区地改总的精度
上述方法只是评价了DEM的精度,并没有改变DEM的数据网度,因此,如图1所示的中区地改误差中所包含的两方面误差——DEM地形与实际地形不一致引起的改正误差和计算时选取的质量模型拟合DEM不准确引起的改正误差——在中区地改精度评价时均应予以统计。至于中区地改采用何种算法效果更好,前人已有很多研究[9-14],本文不作探讨。
4.1 质量模型拟合DEM不准确引起的改正误差计算
质量模型拟合DEM不准确引起的改正误差大小和DEM的数据网度有很大关系,网度越密,这部分误差越小。在网度一定的情况下,可采用变换高程数据节点位置(包括平移、旋转)后重新计算中区地改值,利用其与原始计算值的差值进行均方误差统计。计算公式应采用式(3)的同精度检查公式。该误差也就是现阶段重力工作中普遍作为中区地改总误差来统计的那部分误差,其计算统计方法已非常成熟,在此对其不多赘述。应注意的是,这一过程中的前后两次中区地改值计算,均应采用DEM高程,而不应采用实测高程。
4.2 中区地改总精度统计
DEM地形与实际地形不一致引起的改正误差和计算时选取的质量模型拟合DEM不准确引起的改正误差是同时且独立存在的,因此,中区地改总的均方误差应采用式(4)进行计算:
(4)
式中:εgT为中区地改总的均方误差;εgTD为DEM地形与实际地形不一致引起的改正误差的均方差;εgTM为质量模型拟合DEM不准确引起的改正误差的均方差。
以上两部分误差在计算时,如果所有测点都参与了,那么也可采用式(4)先求出每一个测点的中区地改误差,然后用同精度检查公式进行中区地改总的均方误差统计。
5 应用实例
以青海门源回族自治县幅、山丹县幅1∶25万区域重力调查项目为例,对上述中区地改精度评价方法进行进一步说明。
5.1 工作区地形特征
工作区大部位于祁连山中部,东北部分为河西走廊和阿拉善地区,中间以龙首山相隔,地跨甘肃、青海、内蒙古3省区。
工作区中部祁连山地势较高峻,海拔4 000 m以上的山峰比比皆是;北段地势不高,在龙首山脉以北地势较低,海拔在1 500 m左右,龙首山脉为北端最高地段,海拔在3 000 m以上,最高点海拔3 616 m;在祁连山脉与龙首山之间,海拔在1 000~2 500 m之间,为著名的河西走廊。南段地势较高,由一系列山脉及山间盆地构成,其中与青海湖相接处海拔较低,大约3 200 m,最高峰在祁连山脉,海拔5 200 m以上,山间谷底海拔也在3 500 m左右。
工作区位于青藏高原边部,地形整体高差大,山区地形陡峻,切割剧烈,山间盆地内地形相对平坦。
5.2 工作区重力测点实测三维坐标精度
重力测点三维坐标采用GPS载波相位静态差分测量方法进行测量。重力测点三维坐标最终精度(包含控制网误差、观测误差、坐标转换误差):平面均方误差为±1.177 m,最大值为6.402 m;高程均方误差为±0.332 m,最大值为0.927 m。可见,采用重力测点实测高程评价DEM高程精度属高精度检查。
5.3 工作区DEM精度评价
在开始评价前,首先将重力测点实测三维坐标数据和DEM数据转换为同一坐标系统。在DEM中通过内差读取全区5 271个重力测点的DEM高程,采用式(1)计算得到DEM高程的均方误差为7.49 m。
实测高程与DEM高程误差分布直方图见图2。统计分析得出:实测高程与DEM高程差值(hS-hD)最大值64.846 m,最小值-59.009 m;差值绝对值在0~5 m间的测点数为3 281个,占比为 62.25%(其中差值绝对值在0~2 m间的测点数为1 675个,占比为31.78%);绝对值在5~10 m间的测点数为1 203个,占比为22.82%;绝对值在10~15 m间的测点数为498个,占比为9.45%;绝对值在15~20 m间的测点数为171个,占比为3.24%;有118个测点的差值绝对值>20 m,占比为2.24%。
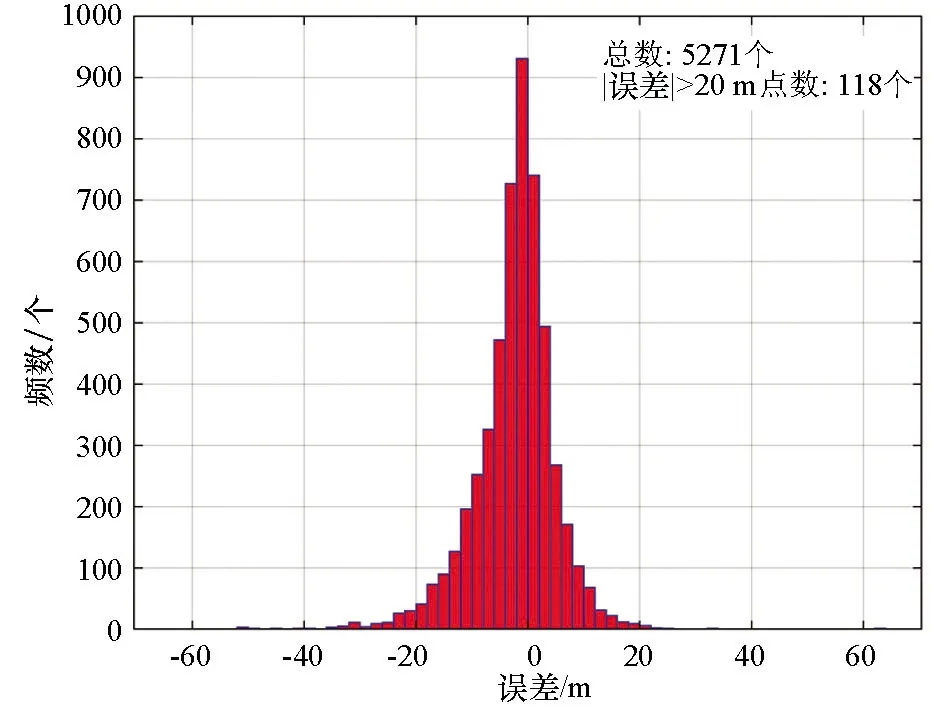
图2 实测高程与DEM高程误差分布直方图
两种高程误差的分布与地形具有明显的对应关系,误差较大的测点基本分布在山区地形起伏变化较大、切割剧烈的区域,而地形相对平坦的区域误差均较小,其特征与表2所表述的一致。由超大误差点(误差值绝对值>20 m)分布与地形的关系图(图3)可以看出,在地形起伏、转折变化剧烈的部位,DEM对地形的描述误差显然是比较大的。
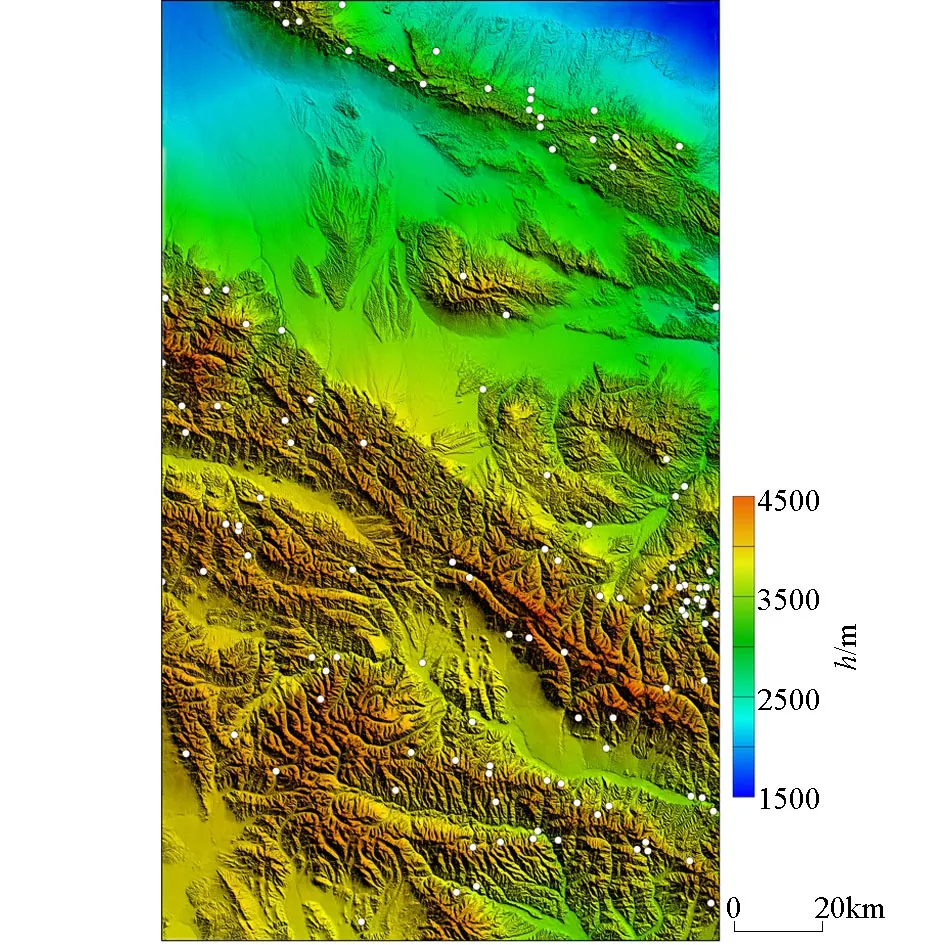
图3 超大误差点(白色圆圈)分布与地形的关系
5.4 中区地改精度
首先,采用抽样法评价质量模型拟合DEM不准确引起的改正误差。全区共均匀分布抽取217个重力测点(占比4.12%),将DEM旋转45°后重新计算中区地改值,用式(3)统计其均方误差,结果为:εgTM=±0.029×10-5m/s2。
其次,计算DEM地形与实际地形不一致引起的改正误差。全区5 271个重力测点全部参与了计算,DEM高程与实测高程计算中区地改误差分布直方图见图4。由于高程超大误差的测点具有明显的粗差,其计算的中区地改误差对最终统计结果影响甚大,但这些点的误差不能代表全区的真实误差水平,因此首先予以剔除。本次统计剔除了高程误差绝对值>20 m的118个测点,剩余5 153个测点用式(1)统计其均方误差,最终统计结果为:εgTD=±0.125×10-5m/s2。

图4 DEM高程与实测高程计算中区地改误差分布直方图
最后,采用式(4)计算出中区地改总的均方误差为:εgT=±0.128×10-5m/s2。
从以上统计结果可见,考虑了由于DEM地形与实际地形不一致引起的中区地改误差以后,得到的中区地改总均方误差明显大于只考虑质量模型拟合DEM不准确一项因素得出的中区地改总均方误差,但这个结果更接近实际误差,同时也说明,DEM地形与实际地形不一致引起的中区地改误差是重力中区地形改正的主要误差来源。
上述方法还有可改进的地方。比如,现在计算DEM地形与实际地形不一致引起的中区地改误差时,采用的还都是相同的DEM数据,只是测点高程采用了不同的值,如果能采用某种算法对测点附近的DEM数据节点进行某种程度的修正,也许计算的中区地改误差值更接近实际误差值,这还需要进一步深入研究。
6 检查结果的拓展应用
中区地改中两部分误差的统计均可按规范要求进行5%~10%的抽样检查。但笔者建议全工作区所有测点均参与检查,这可以为我们提供许多信息。例如,在区域重力调查工作中,中区地改所用DEM数据可能具有不同的来源,精度也不一致;可以通过绘制高程误差分布图、中区地改误差分布图及超差测点点位图等方法,来分析工作区内不同区域DEM的精度情况、中区地改误差的分布情况及超差点的分布情况。如果出现区域性连片的超差情况,则应考虑获取其他精度更高的DEM[15-16]来重新完成这一区域的中区地改。即便无法解决,也可以做到心中有数,在后期的数据处理及解释推断过程中,对这一区域的重力异常有正确的认识。
另外,现在进行中小比例尺重力调查时,一般远区的重力地形改正也都和中区地改一样采用DEM数据进行计算机改正,因此,该精度评价方法可以扩展至远区。
7 结论
重力中区地改所用DEM数据是前人测量、加工形成的数据,因此,其在测量、加工过程中已经包含了误差。通过对DEM数据误差的来源及大小分析,并采用实际资料对比可见,在山区等地形起伏变化较大的地方,这个误差还是很大的,对重力中区地改精度的影响是不能忽视的。但是,如何评价这个影响,也是比较困难的。本文提出这种利用测点实测高程进行重力中区地形改正精度评价的方法,目的就是想通过具有可操作性的方法,来获取更接近中区地改误差真实水平的统计结果,为后续的研究工作打好基础。但是,该方法毕竟是针对不具备DEM精度检查条件时对中区地改精度的一种替代评价方法,有一定的局限性。这些方法都采用了等量代换的思路,哪一种方法计算的结果更接近实际误差值,还需要在不同地形条件下进行大量的对比试验,这是下一步研究的方向。
本文的目的主要是希望引起大家对现阶段重力工作中中区地改精度评价不全面问题的重视,同时希望能抛砖引玉,大家共同探讨,集思广益,提出更好的解决方案,使重力中区地改的精度统计结果更符合实际。

