入口参数对旋流反应器流场影响的数值模拟

张浩高飞张明阳时国锋

(1.山东建筑大学 热能工程学院，山东 济南250101；2.山东省绿色建筑协同创新中心，山东 济南250101；3.山东建筑大学 党委校长办公室，山东 济南250101)

0 引言

烷基化汽油是一种含烃类的混合物，其辛烷值较高、稳定性好，不会引起爆燃，同时含硫量非常低，而且几乎没有芳烃、烯烃，与低品质汽油调和后能够减少汽车尾气中有害气体的排放，成为理想的汽油调和组分[1-2]。制备烷基化汽油的传统烷基化反应设备存在一定弊端[3-5]，不能及时将反应产物分离出去，造成反应过程的不连续性，不利于生产进行，同时反应产物分离不及时会造成副反应增多，反应产物收率和质量下降。

通过对水力旋流器的研究发现，其内部流场在提高两相混合水平的同时可实现反应产物及时分离，且为无动部件，能耗成本低[6-7]。基于水力旋流器的结构特点以及烷基化反应的性质，一种适用于烷基化反应的新型液—液旋流反应器应运而生。为了能够实现在反应器内部催化剂与反应物充分混合，并能同时完成目标产物与催化剂的及时分离，在单一设备中能够耦合混合、反应及分离单元过程，实现既能充分混合反应，又能防止副反应的发生，需要优化反应器的结构，提高目标产物的质量和收率。

旋流反应器内部为强湍流场，其分布极为复杂，通过实验手段很难准确地测量流场分布。近年来，随着计算流体力学(Computational Fluid Dynamics，CFD)的快速发展，利用其模拟复杂流场的分布特性成为研究复杂流场一种新的手段。杨密等[8]基于CFD技术研究了入口角度对短接触旋流反应器流场的影响，发现倾斜向下10°的切向入口能有效地消除顶部灰环、抑制轴向返混，减少在混合腔的停留时间，同时改善混合腔内的固相颗粒不均匀度。张明阳[9]利用软件Fluent模拟了离子液体烷基化用旋流反应器内混合与分离行为，着重分析了入口总流量，溢流比和进料比对反应器内速度场、浓度场、压力场及混合行为的分布规律。文章利用Fluent数值模拟了不同切向缝入口个数下旋流反应器的内部流场，在其他参数不变的条件下，研究反应器结构参数对混合、分离行为的影响，分析流场分布特性及不同切向缝入口个数对温度场、浓度场的影响规律。

1 数学模型

1.1 多相流模型

在旋流反应器中，不能忽略分散相体积分数，反应器两相间存在互相贯穿的现象，所以Fluent模拟中选择欧拉-欧拉(Euler-Euler)多相流模型，在多相流模型中选择欧拉(Eulerian)模型[10-12]。

q相的体积Vq由式(1)表示为

式中αq为相体积分数，满足

对于q相，连续性方程由式(2)表示为

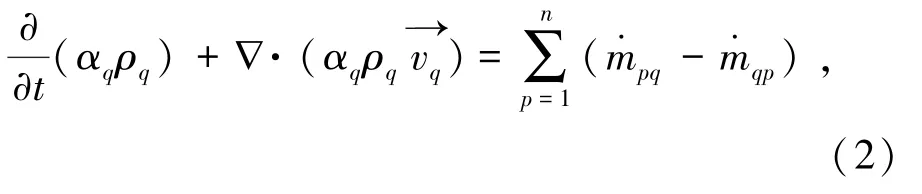
第q相的动量方程可由式(3)表示为

1.2 湍流模型

旋流反应器内部具有强湍流运动，选择的湍流模型为雷诺应力模型(Reynolds Stress Model，RSM)[13-15]，其通过求解雷诺应力的传递方程和耗散率方程对纳维-斯托克斯方程(Navier-Stokes equations)进行封闭。雷诺应力输运方程可由式(4)表示为

式中t为时间；ρ为流体密度；u′为速度脉动量；当i取1、2、3时分别表示x、y、z方向，j、k同理；DT，ij为湍动扩散项；DL，ij为分子扩散项；Pij为雷诺应力产生项；Gij为浮力产生项；φij为压力应变项；εij为黏性耗散项；Fij为系统自转产生项。

流动能方程(k方程)由式(5)表示为

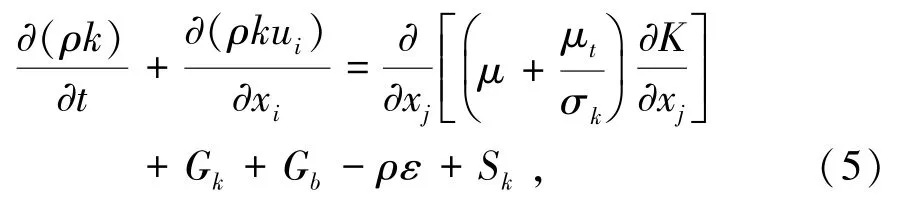
湍流能量耗散率方程(ε方程)由式(6)表示为

式中k为湍动能；ui为速度；ε为湍流耗散率；μ为粘性系数；GK为层流速度梯度产生的湍流流动动能；Gb为浮力产生的湍流动能；SK和Sε为自定义；C1ε＝1.44、C2ε＝1.92；C3ε为与重力矢量相对应的局部流动方向的函数；σk＝0.82、σε＝1.0。

2 几何模型与参数设置

2.1 几何模型建立

旋流反应器结构示意图如图1所示。建立直角坐标系，坐标原点在反应腔与分离腔交界处，竖直向上为z轴正方向。连续相通过连续相入口进入旋流反应器，并经导流叶片形成下行旋转流进入反应腔，分散相则由切向缝形成水平旋转流进入反应腔，两者最先在壁面处接触，进而发生碰撞、破碎、混合反应，之后下行进入分离腔，轻相由顶部溢流口流出，重相则由底部底流口流出，完成混合反应分离过程。

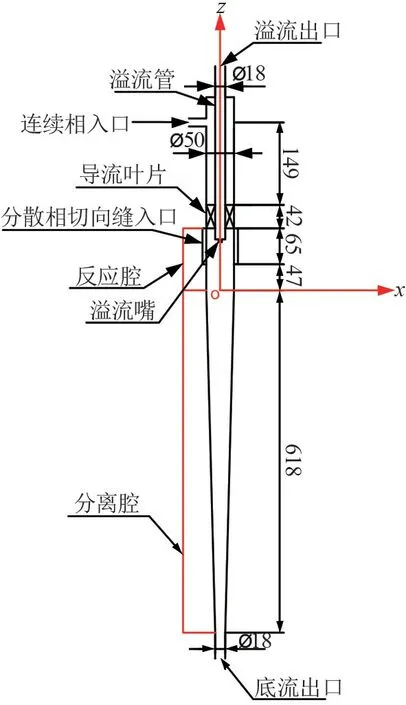
图1 旋流反应器结构示意图/mm

2.2 网格划分

考虑到旋流反应器内部结构的相对复杂性，选用非结构网格划分模型。经过网格独立性验证，物理模型网格数约为35万，网格质量控制在0.32以上；对流动剧烈的区域如切向缝入口、反应腔、导流叶进行网格局部加密，网格大小控制在0.2；分离腔区域网格大小控制在0.4。网格划分如图2所示，左边第一张为反应器整体网格划分正视图，右边4张分别对应切向缝入口个数为1、2、3、4时的网格划分俯视图。

图2 网格划分示意图

2.3 边界条件设定

模拟计算采用有限体积法进行离散，离散格式采用QUICK格式，压力差值格式采用PRESTO格式，压力速度耦合项采用压力耦合方程组的半隐式方法(Semi-Implicit Method for Pressure Linked Equations，SIMPLE)。

(1)入口边界条件

采用速度入口，根据入口流量和入口截面积计算得到入口速度v。

(2)湍流强度

湍流强度I由式(7)表示为

式中Re为雷诺数，为水力直径，mm。对于圆管，水力直径等于圆管半径。连续相水力直径为26 mm，湍流强度为6.87%；分散相水力直径为15 mm，湍流强度为4.88%。

(3)出口边界条件

旋流反应器的溢流管和底流管的设计管长均是相应管径的10倍以上，可认为出口处为完全发展状态，选用自由出流outflow。

(4)采用无滑移边壁条件，壁面粗糙度为0.5。

2.4 流体的物性参数

选用煤油作为分散相液体，以质量分数为74%的甘油水溶液作为连续相液体。所选用两相流体的物性参数见表1。相对于连续相，分散相液体的密度要小近一倍，两者在旋流反应器中的混合反应有利于在分离腔中实现及时分离，提高目标产物收益。

表1 两相流体的物性参数表

3 模拟结果分析

3.1 典型截面选取

为了能更好地比较在不同的切向缝入口个数影响下旋流反应器内的流场分布，进一步分析反应器内两相的混合分离性能，选取流场内3个典型截面进行比较分析，截面位置如图3所示，z从上到下依次选取为65、0和-200 mm。其中，z＝65 mm位于切向缝入口处、溢流嘴附近；z＝0 mm位于反应腔和分离腔的交界处；z＝-200 mm位于分离腔下端位置。

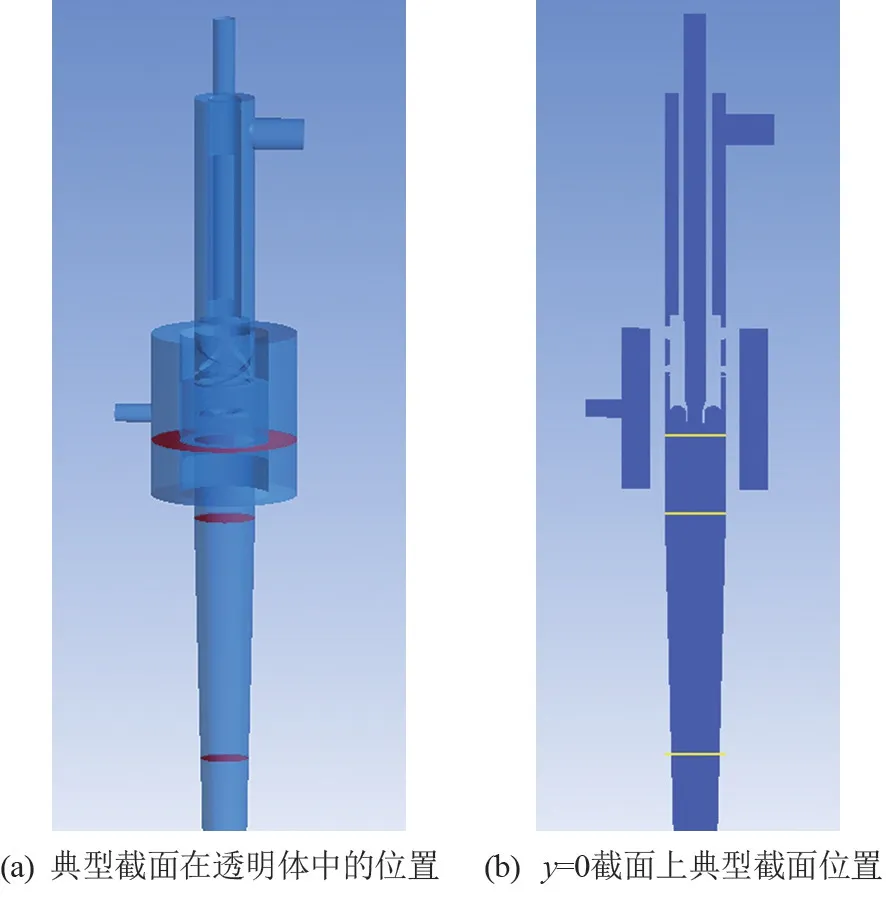
图3 典型截面在模型中的位置示意图

3.2 切向速度在典型截面处的分布特性

分散相从旋流反应器的切向缝进入反应腔形成水平旋转流，连续相在导叶的作用下形成下行旋转流进入反应腔，使得流场中分散相液滴受到剪切力的作用，并沿径向存在速度梯度。剪切力能够使分散相液滴发生破碎和聚并行为，剪切力越大，分散相越容易破碎成小液滴，有利于增大两相接触界面面积，提高混合程度。同时，切向速度是3个速度分量中最为重要的，决定了流场中混合液体所受离心力的大小，能够直接影响两相的分离效果，因此研究切向速度对认识流场的混合分离性能尤为重要。

在保证入口总流量、溢流比、进料比为最佳配比条件时，旋流反应器在不同的切向缝入口个数下流场中切向速度随径向、轴向的分布规律如图4所示。以r表示径向位置，r＝0 m为坐标原点，正、负号为原点两侧x轴正、负方向，n为切向缝入口个数。整体上来说，3个截面的切向速度均围绕中心对称分布，方向一致，在中心位置附近切向速度逐渐减小为零。原因是受到的轴向力最大，形成上行流区域，由于反应器壁面采用了无滑移边界条件，存在一定的粗糙度，流体边界层上的切向速度也逐渐减小到零。在z＝65 mm截面处，切向速度围绕中心大体呈现双“M”分布，在壁面附近r＝±0.022 m和中心附近r＝±0.005 m出现切向速度的极大值，在r＝±0.015 m附近切向速度较小，此时分散相液滴受到的离心力较小，不利于两相的分离。但由此增加了两相接触时间，有利于反应的充分混合。进一步分析发现，随着切向缝入口个数的增加，切向速度线逐渐下移，切向速度最大值逐渐减小，并随径向往中心处移动。说明在反应腔两相入口位置，切向缝入口个数越多，切向速度越小，离心力越小，越有利于两相的混合。

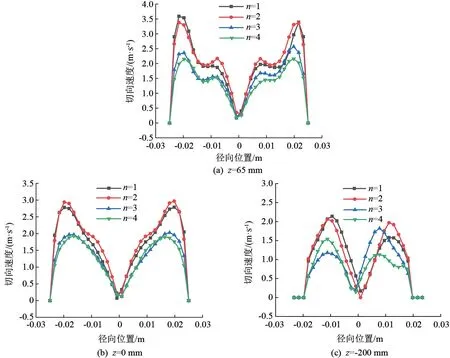
图4 典型截面切向速度分布图

随着轴向位置下移，相同的切向缝入口个数下，切向速度的最大值逐渐减小，且出现的位置往中心处移动。说明随着轴向位置的下移，由于壁面无滑移和流体的黏性作用能量损失逐渐增多。在z＝65 mm和z＝0 mm截面的边壁处，由于靠近两相的入口使得切向速度急剧增加，n为1和2时的切向速度变化大体一致，且变化幅度明显大于n为3和4时的切向速度。z＝-200 mm的截面位于分离腔底部，此处分离腔的截面积变小。不同的切向缝入口个数对应不同变化的切向速度，整体变化为入口个数越少，切向速度越大，对应的离心力越大，有利于混合物的分离，同时当n为奇数时出现了切向速度围绕中心的不对称现象。

3.3 轴向速度在典型截面处的分布特性

轴向速度在旋流反应器中分为上行流区域和下行流区域，两者速度方向相反，并以速度为零的截面作为两者的分界面。轴向速度通过影响两相的混合时间进而影响两相的混合分离效果。在保证入口总流量、溢流比、进料比为最佳配比条件时，旋流反应器在不同的切向缝入口个数下，流场中轴向速度随径向、轴向的分布规律如图5所示。整体上看，不同切向缝入口个数下的轴向速度都以径向位置r＝0 m呈现轴对称分布，由于采用了无滑移边壁条件，所以在壁面边界层处轴向速度逐渐减小到零。进一步分析z＝65 mm截面发现，在-0.01 m＜r＜0.01 m区域内，轴向速度先急剧增大后急剧减小，且入口个数n＝2时变化程度最大，n＝3和n＝4变化程度相同，说明在这一区域切向缝入口个数越多，轴向速度越小，混合时间越长，有利于两相的混合反应。随着轴向位置下移，该区域对应的轴向速度减小，表现为反应腔区域n越大轴向速度越小，混合时间增加，分离腔区域由于能量的损失和截面积的变化，不同n对应的轴向速度变化趋势并不规律。分析z＝65 mm和z＝0 mm位置发现，在r＝±0.015 m区域附近，轴向速度变化缓慢，对照切向速度图发现切向速度处于一个极小值位置，切向速度梯度小，说明在这个区域离心力小，增加了两相的接触时间，有利于充分混合反应。同时越靠近两相的入口位置，这个区域的范围越大，且切向缝入口个数在这一区域越多，切向和轴向速度也越小，有利于混合反应的进行。

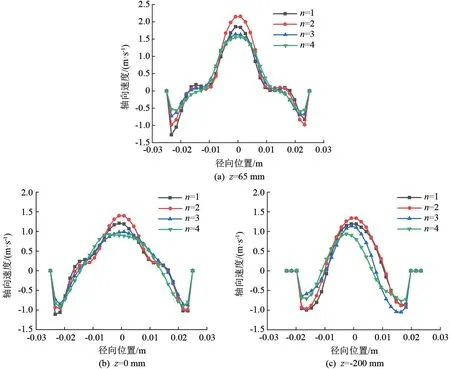
图5 典型截面轴向速度分布图

随着轴向位置的下移，轴向速度为零的点的位置逐渐往中心处移动。将旋流反应器轴向速度为零的点(除壁面附近为零的点之外)的轨迹绘制成曲线，即轴向零速包络面，模型如图6所示。轴向零速包络面将旋流反应器的流体区域分为两部分，且呈现出与反应器分离腔锥角角度一致的变化趋势，与前人的研究结果一致[16-17]。

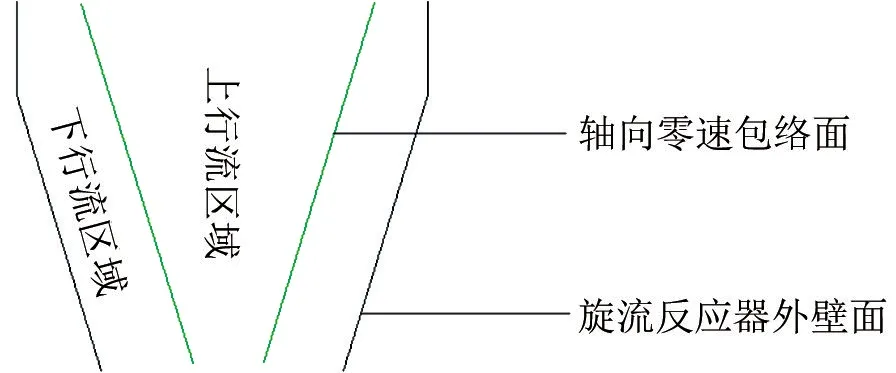
图6 轴向零速包络面模型图

3.4 不同截面上的体积百分浓度分布

3.4.1y＝0截面上的浓度分布

分散相浓度云图能够直接反映出分散相在旋流反应器内的分布情况，在宏观上有助于分析分散相与连续相的混合分离程度。在其他参数不变的情况下，不同切向缝入口个数下，在y＝0截面上旋流反应器内的分散相浓度分布如图7所示。分散相主要集中分布在入口区域、入口缓冲腔、圆柱段反应腔、分离腔上部和溢流管中，而在壁面附近和底流管中浓度相对较低。两相在入口区域和缓冲腔中不接触，所以主要在反应腔和分离腔上部进行混合反应。由于离心力的作用和分离腔截面的减小，反应后的分散相在连续相的推挤下往中心处靠拢，最终形成倒流由溢流管流出，所以溢流管中分散相浓度较大。进一步分析发现，当切向缝入口个数n＝1时，溢流管中分散相浓度最大，底流管中最小，说明其分离效果最好；随着n的增大，溢流管中分散相浓度逐渐降低，底流管中浓度逐渐增加，分离效果逐渐变差。当n＝1时，圆柱段反应腔中分散相浓度较大的区域最广，即混合区域最大；而n＝2时，分散相浓度在反应腔分布最为集中，且集中分布在反应腔中心位置，说明其混合效果最好；而随着切向缝入口个数的增加，反应腔中分散相浓度逐渐降低，混合和分离效果逐渐减弱。

图7 y＝0截面上的体积百分浓度分布图

3.4.2 典型截面上的浓度分布

在z分别为65、0、-200 mm的典型截面，不同切向缝入口个数条件下分散相浓度分布情况如图8所示。在z＝65 mm处的截面，n＝1对应的分散相浓度在反应腔中分布范围大，而n＝2时分布效果最好，随着n增大，在边壁处出现了分散相浓度聚集现象。由于两相最先是在反应腔壁面处相遇，随即发生碰撞破碎，分散相在在离心力、向心浮力和液体阻力作用下，产生径向离心沉降速度，便开始往中心处沉降。随着n增大，分散相不能及时往中心处移动，由此增加了分散相在壁面的浓度。在z＝0 mm处，n＝4时出现了浓度不对称分布现象，且随着轴向位置的下移，n越大，分散相浓度的不对称分布现象越明显，且当n＞2时，分离效果逐渐变差。

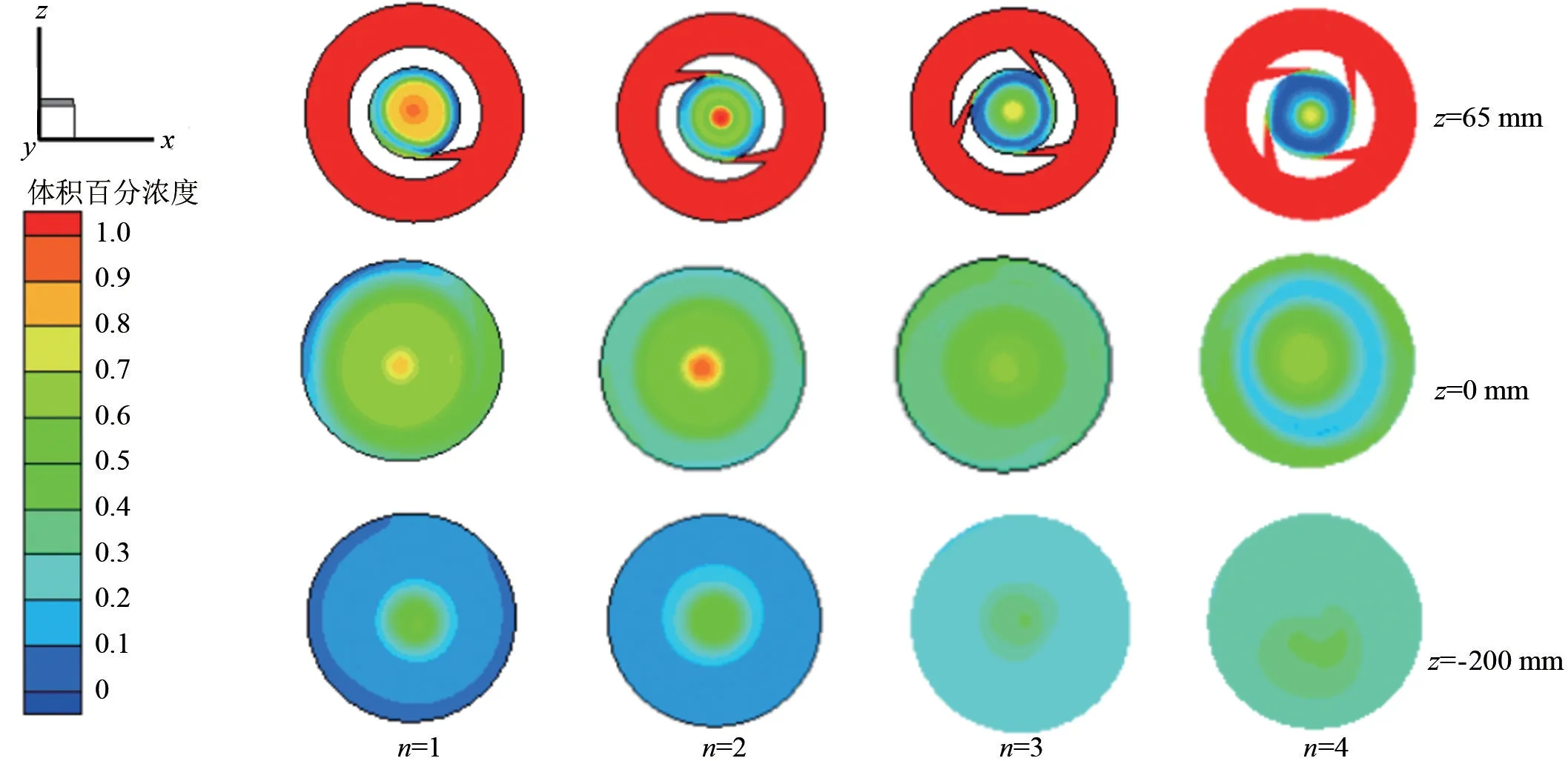
图8 典型截面上的体积百分浓度分布图

4 结论

利用软件Fluent模拟了不同切向缝入口个数下旋流反应器内部流场，分析了不同截面上的速度场、浓度场分布特性及入口个数对其影响规律，主要结论如下:

(1)在反应腔两相入口位置切向缝入口个数越多，切向速度越小，离心力越小，越有利于两相的混合；在分离腔区域，入口个数越少，切向速度越大，对应的离心力越大，有利于混合物的分离。

(2)随切向缝入口个数增多，反应腔内轴向速度越小，混合时间越长，有利于两相的混合反应，反应器内轴向零速包络面将流场分为轴向速度方向相反的上行流区域和下行流区域。

(3)分散相浓度在混合区域和分离腔上部较大，说明两相的混合反应在这些区域进行；随着切向缝入口个数的增加，反应腔中分散相浓度逐渐减小，分离腔中分散相浓度逐渐增大；对照典型截面处的浓度场可知，当切向缝入口个数为2个时，反应器整体混合分离效果最好。