精密线型控制网建立方法的探讨

王健

(华北理工大学 矿业工程学院，河北 唐山 063210)

0引言

“自由测站边角交会”是建立精密线型控制网的一种方法，广泛应用于高速铁路轨道控制网的建立中。该方法无需对中，仅需观测方向和距离值，使用自动全站仪时，具有自动化程度高、精度和可靠性高等优点[1]。近年来，该方法也逐步推广到隧道地下控制网、地铁控制网等线性工程中[2]。但是，该方法每个测站都要对10余个方向进行观测，对通视条件要求高，常常由于不满足通视条件而造成建网困难。精密边角网是一种传统的控制网建立方法，具有精度高、可靠性高等特点，常常应用于精密工程控制网的建立中[3]，但是目前其在线型工程中应用较少。该研究从控制网形、外业观测工作量、工作效率和精度等方面，对边角网和自由测站边角交会网进行了比较，提出了利用边角网建立精密线型控制网的方法。

1精密线型边角网的建立方案

1.1 控制点的布设和控制网型分析

高速铁路的轨道控制网CPIII(即自由测站边角交会网)如图1所示，控制点成对布置，一对控制点的间隔10 m左右，点对之间的间隔约60 m左右。自由测站边角交会网的点位都是在路基的桩基、桥梁的防护墙、隧道的边墙上设置强制归心棱镜，以减小对中误差的影响。采用自由测站边角交会模式测量，全站仪安置在2个点对组成的四边形大致中心位置，向前、后各3对控制点上的棱镜进行全圆方向和距离观测，测站之间重叠4对控制点。利用该控制网进行自由设站后，配合轨道测量小车测定轨道的位置，能保证轨道的中心位置及轨道的平顺性。

图1 自由测站边角交会网

自由测站边角交会网对通视条件要求高，在个别路段可能会造成建网困难，此时可以考虑利用边角网来建网。精密线型边角网在选点、布网时应满足以下要求：(1)点位布设于路基顶面上，便于利用高精度全站仪对构件进行精密放样；(2)构成的网型结构强度高，图形简单；(3)网中避免有过短的边，以便减小短边对角度测量精度上的不利影响。按照以上要求，在自由测站边角交会网的基础之上，建立如图2所示的精密线型边角网，沿线路每隔60 m左右布设一个控制点，相邻控制点分别位于线路的左侧和右侧。精密线型边角网的每个控制点上，都要设置强制对中观测墩，以减小对中误差的影响。在每个测站上，都要对5个相邻点进行方向和距离观测。

图2 精密线型边角网

1.2 控制网工作量、工作效率等方面的比较

(1)在工作量方面，对2种方法进行比较如下：

自由测站边角交会网：相邻测站间隔约120 m，每千米约设站8.3站，每测站观测12个方向值和距离值，每千米观测约100个方向值和距离值；

边角网：相邻测站间隔约60 m，每千米约设站16.7站，每测站观测5个方向值和距离值，每千米约观测83个方向值和距离值。

边角网虽然每千米观测的方向和距离数量略少，但设站数量多，2种方法的工作量大体相当。

(2)在工作效率方面，按照一般测量工人的操作仪器的水平，对2种方法进行比较如下：

自由测站边角交会网：每测站观测大约需要25 min，每次搬站大约需要4 min，完成每千米的观测任务大约需要4.0 h；

边角网法：每测站观测大约需要12 min，每次搬站大约需要2 min，完成每千米的观测任务大约需要3.9 h。

从上面的比较看，2种方法的工作效率大体相当。

(3)2种控制网在埋设点位的投入方面：

自由测站边角交会网每千米布设控制点33.3个，每个点位上需设置强制归心棱镜，当工程路段已有相应的结构物(如桥梁的防护墙、隧道的边墙等)时，需要投入的较少；

边角网每千米布设控制点16.7个，每个点位都要设置观测墩，建立观测墩的投入稍大。当工程路段上的控制点必须建立观测墩时，即使边角网每千米控制点数量少，其埋设点位的投入费用也稍大。

2控制网精度方面的比较

2.1 基本思路

对于2种控制网的精度比较，其基本思路是：

(1)根据图1和图2所示的2种控制网点位间的相对位置关系，假定各控制点的真实坐标值；

(2)按照计算的控制点坐标和图1和图2所示的网型，计算各测站的不含误差的方向值和距离值；

(3)生成符合正态分布N(0，σ2)的随机误差值；

(4)将各测站不含误差的方向值和距离值加上生成的随机误差值，生成符合N(μ，σ2)分布的模拟观测值；

(5)对生成符合正态分布的模拟观测值，按间接平差方法进行平差计算和精度评定；

(6)比较和分析2种控制网的精度情况。

2.2 假定各控制点的真实坐标值

对于自由测站边角交会网控制点的坐标计算，按照图1，假定控制点沿设计线路布设，相邻点横向间隔10 m，纵向间隔60 m。以左下角12点为原点，以线路横向为X轴、纵向为Y轴建立独立平面直角坐标系。计算各点坐标，结果见表1。按照相同的方法确定边角网各控制点的坐标，计算结果与自由测站边角交会网同名点坐标相同。

表1 自由测站边角交会网各控制点的假定坐标/m

2.3 计算各测站的不含误差的方向值和距离值

按照图1的网型，假设自由测站边角交会网相邻测站间隔120 m，每一测站位置为相邻4个CPIII点构成矩形的中心，计算测站至各控制点的坐标方位角和距离。如表2以测站b的计算结果为例。

表2 自由测站边角交会网测站b的方向、距离计算结果

对于边角网，按照图2的网型，根据各控制点的坐标计算相应的方位角和距离。以测站31为例，计算结果如表3所示。

表3 边角网测站31的方向、距离计算结果

2.4 生成符合正态分布N(μ，σ2)的模拟观测值

(1)生成符合正态分布的随机误差，其方法为：

首先，利用计算机的随机数发生器，生成一组在区间(0,1)上均匀分布的伪随机数序列i。然后，把伪随机数序列i变换为服从标准正态分布N(0,1)的随机数bi，其方法为[6]：

(1)

(2)

式中，i、i+1分别为伪随机数序列上的相互独立的(0,1)区间上的均匀随机数。

(2)生成服从正态分布N(0，σ2)的误差

(3)

σ为观测值的中误差。本次试验中，测角中误差取1.8 s，测距中误差取1 mm+1*10-6D。

(3)生成服从N(μ，σ2)的观测值

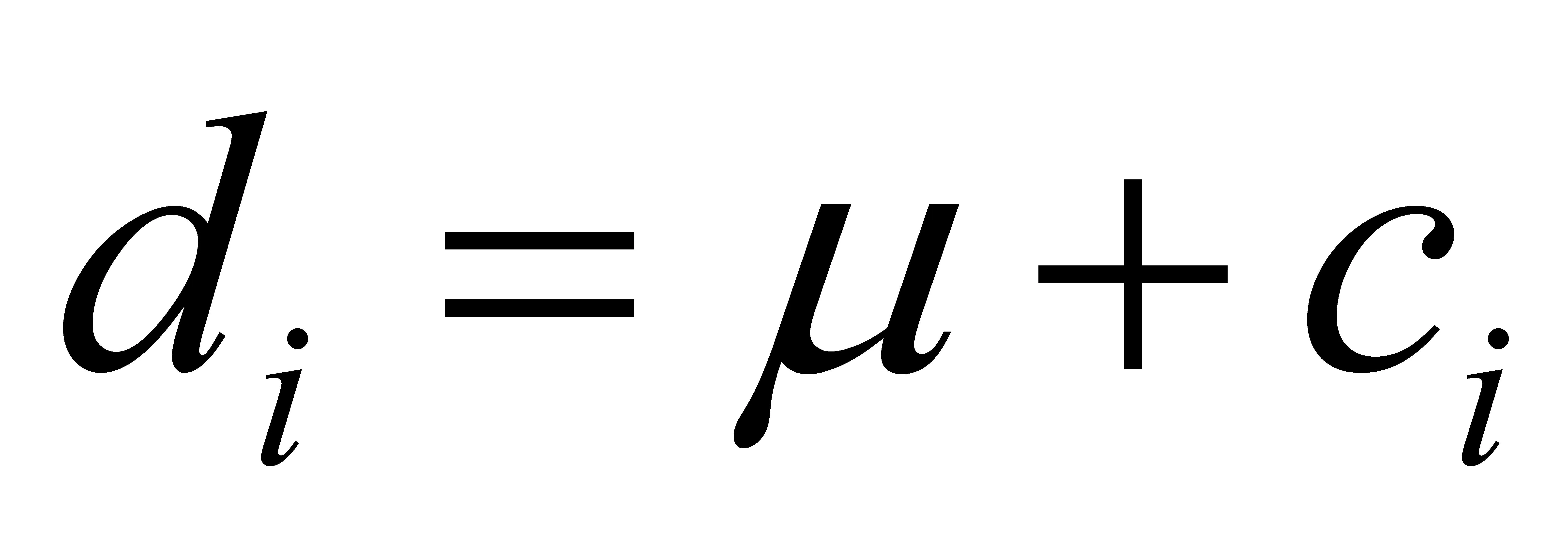
(4)

μ为标题2.3中计算的不含误差的方向值和距离值。

2.5 平差计算和精度评定

(1)观测值的权矩阵的确定

测角中误差为1.8 s(将其设置为先验单位权中误差)，测距中误差为1 mm+1*10-6D。从而确定观测值的权矩阵为：

(5)

(2)按照间接平差确定误差方程

对于角度观测值，其误差方程为[7]：

(6)

对于边长观测值，其误差方程为：

(7)

(3)求解各点坐标并进行精度评定

按照以上方法对2种控制网进行了平差计算。自由测站边角交会网的计算结果见表4，后验单位权中误差为1.27，多余观测值总数为40，平均多余观测值数为0.5，可靠性高。边角网的计算结果见表5，后验单位权中误差为1.57，多余观测值总数为28，平均多余观测值数为0.58，可靠性高。

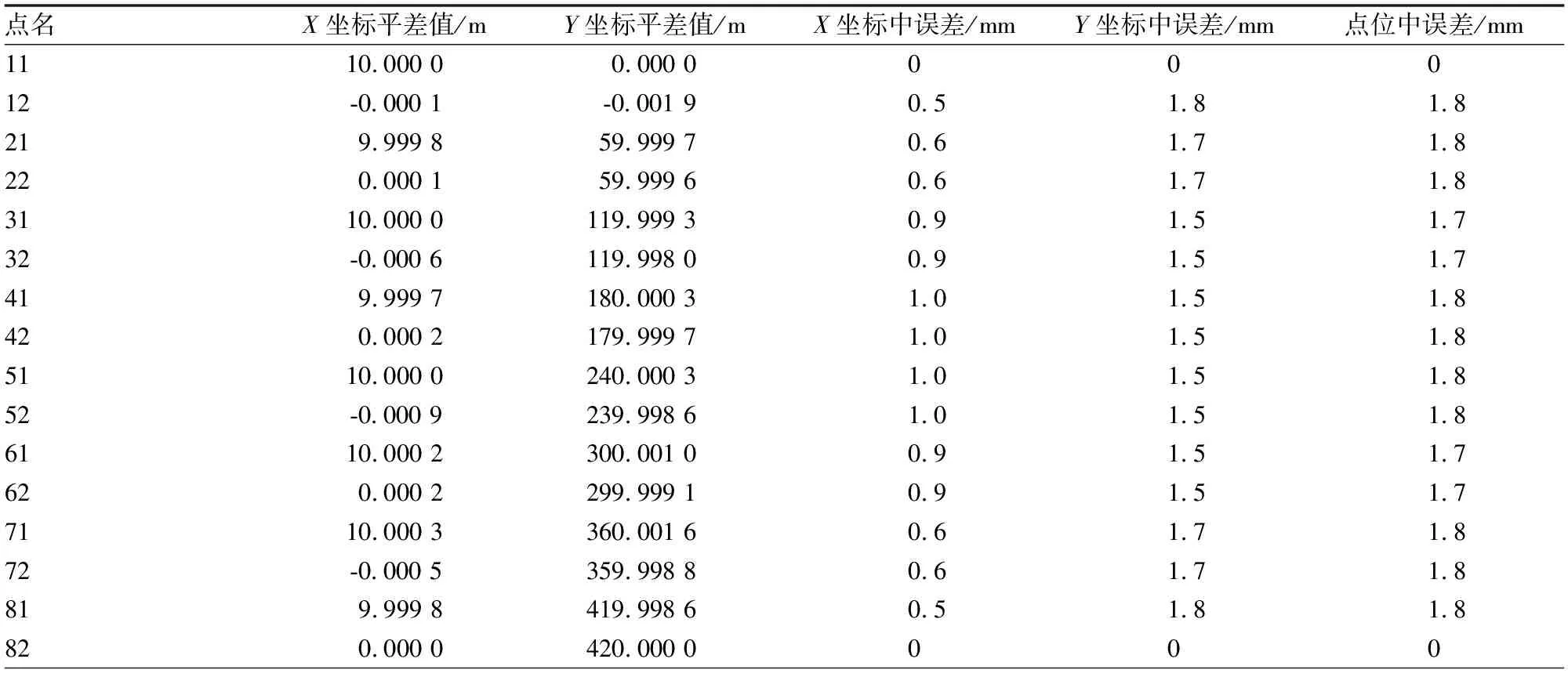
表4 自由测站边角交会网平差结果

表5 边角网平差结果

2.6 2种控制网的精度比较

由表4、表5可得：在相同的测角、测距精度下，自由测站边角交会网的最大点位中误差为1.8 mm，平均点位中误差为1.8 mm；边角网的最大点位中误差为1.1 mm，平均点位中误差为1.1 mm。由此可见，边角网从精度上明显优于自由测站边角交会网。将2种控制网的平差后坐标与真实值比较，其结果见表6。

从表6可以看出，自由测站边角交会网的点位误差在0～0.5 mm区间的有7个，占比44%；0.5～1.0 mm区间的有2个，占比13%；1.0～1.5 mm区间的有3个，占比19%；1.5 mm以上的有4个，占比25%。边角网的点位误差在0～0.5 mm区间的有4个，占比50%；0.5～1.0 mm区间的有1个，占比13%；1.0～1.5 mm区间的有3个，占比38%；1.5 mm以上的有0个，占比0%。可见边角网在精度方面明显优于自由测站边角交会网。

表6 2种控制网的平差后坐标与真实值比较的结果

由于偶然误差具有随机性，会导致单次模拟的结果不可靠。因此，按照上面的方法共生成了20套相互独立的模拟观测值，并分别进行了平差计算和精度评定。结果表明，虽然不同的模拟观测值的平差结果和精度评定结果略有不同，但总体来说与上面的结果一致，表明边角网的精度高于自由测站边角交会网。

3结论

(1)2种控制网在外业工作量、工作效率方面大体相当。

(2)在测角、测距精度相同的情况下，精密边角网的精度优于自由测站边角交会网。

(3)与自由测站边角交会网相比，精密边角网每测站观测的方向数少，对通视的要求较低，更能适应通视条件差的线型工程路段。

(4)自由测站边角交会网适合于结构体上便于设置固定棱镜的工程路段，例如隧道的边墙、桥梁的防护墙。边角网适合于便于建立强制观测墩的工程路段，例如稳定的路基上。

(5)自由测站边角交会法设站灵活、无需对中、仅需观测方向和距离值，在使用自动全站仪时，能更好地发挥其自动化程度高的优点，可作为精密线型控制网的主要建网方式；边角网可以作为其有益的补充，在条件合适的路段建立精密边角网，发挥其精度高、对通视条件要求低的优势。