基于copula聚类模型的协同风险度量

刘明成

(重庆工商大学 a.数学与统计学院；b.经济社会应用统计重庆市重点实验室，重庆 400067)

1963年由Baumol[1]提出的VaR风险度量法对于衡量单个金融风险有很好的效果，但无法对系统性风险的外部性和溢出效应做出测度，2011年Adrian和Brunermeier[2]所提出的条件风险价值CoVaR方法，有助于解决这一问题。CoVaR被称为协同风险法，也称条件风险法，其中的“Co”表示的是金融单位之间所具有的联动、传染和条件三种性质。相比而言，两者的差别主要在于VaR只能够测量机构在危机出现前的风险，而CoVaR能够测量出当危机发生时的风险程度；同时，VaR方法应用的对象是单个机构，而CoVaR不仅能描述系统性风险，还可以描述多个机构之间的风险溢出情况。因此，CoVaR方法具有更为先进的特性。万军等[3]通过CoVaR的方法对利率和股市之间的风险溢出效应进行探究，证明了两者之间的风险存在着相互溢出的现象，学界也基于Engle等对CoVaR的研究以及Bassett等所提出的分位数回归发展出了通过分位数的方法计算CoVaR[4-5]。Girardi等[6]收集了大量金融机构的数据之后，利用Garch-CoVaR模型计算了各组综合风险对系统性风险的贡献度，对比分析了各个机构系统性风险的联系特征。而金融资产之间存在复杂的相依结构，不是简单的线性关系，当极端事件发生时，在正态分布和线性相关的假设之下进行风险测算，得到的结果与实际情况会有较大的偏差。Sklar[7]提出的Copula函数就成了衡量多个金融资产风险之间相依关系的有力工具。张尧庭[8]的研究证实了Copula函数在金融方面运用的可行性，并且对其定义、性质等进行了较为详细的介绍。王周伟等[9]利用Copula-CoVaR模型对金融市场整体的风险进行了测量，得到了比传统的分位数回归测量方式更优越的结果。混业经营下金融机构所拥有的基础金融产品的数量庞大，若是单纯地逐一进行CoVaR度量，实际操作过程会非常繁琐。陈振龙等[10]提出基于藤Copula分组模型的金融市场风险度量方法解决了这一问题，同时周全等[11]提出利用分组Copula-CoVaR模型通过事先对金融产品进行分组，再用Copula进行连接，寻找到了更加精确的风险度量方法。本研究提出先用聚类方法分析，然后与Copula相结合的t-Copula聚类-CoVaR模型来分析金融市场的协同风险。

1 相关理论及方法

1.1 CoVaR的定义

传统的风险度量工具VaR是在险价值(value at risk)的缩写，是进行风险测度的一个重要的工具。其意义是当资产价值波动时，在一定的概率水平下，投资者或金融机构所持有的资产在未来的一段时间内产生最大可能的损失。用公式表示为

∆P为单一资产或组合资产在持有期内的损失，VaR为执行水平α下的风险价值。这一公式由Adrian和Brunermeier提出，表示在一定概率水平下，某一金融机构的风险VaR值一定时，其他金融机构的最大可能损失。

在机构i陷入危机，其损失为时，则机构j的VaR值为

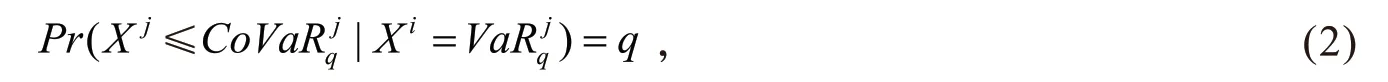
其中，X i表示机构i的收益率。通过CoVaR可以测度单个机构破产对系统性风险的影响，从而可以量化单个机构对整个金融系统的重要性。假定j是整个金融系统，机构i对整个金融系统j的系统性风险贡献为

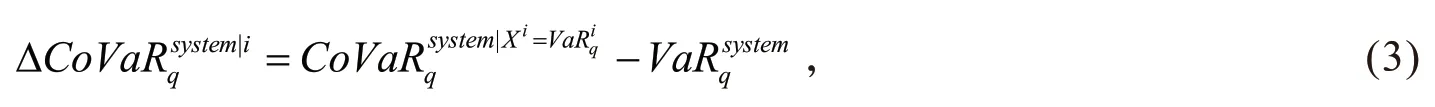
1.2 K-均值聚类算法

金融投资机构所持有的金融产品往往数量众多，若用每一个金融产品依次测度整个机构的条件风险则太过繁琐，所以本研究从金融产品收益率的相似程度着手，将收益率相似的金融产品归为一类，从而达到降维的目的。

K-均值聚类算法是动态聚类中的典型算法，在1968年由MacQuean提出，在各领域都具有广泛的影响力。算法开始时先将要被分类的数据分为K个组，之后从样本中随机挑选出K个对象作为聚类中心，由此计算每个数据与K个聚类中心之间的距离，进行临近分配，这样聚类中心和分给它们的数据对象就形成一个类别。而当我们每分配一个数据，聚类中心就会被重新计算。由此不断重复直到满足聚类中心不再发生变化时，即误差平方和局部最小，就形成了最终的聚类情况[13]。

1.3 基于Copula函数的CoVaR计算

Copula函数的概念最早是由Sklar提出的，其在统计学上的作用是将多个单独的分布函数通过Copula函数作用成一个联合分布[14]，能够刻画出多个变量之间的非线性相关关系，同时也可以描述变量之间的尾部相关性。相比于分位数回归，Copula函数对金融数据的风险价值计算有更好的效果。表现函数为

其中C(⋅,…,⋅)就是一个Copula函数，那么就可以得到多元分布的概率密度函数为

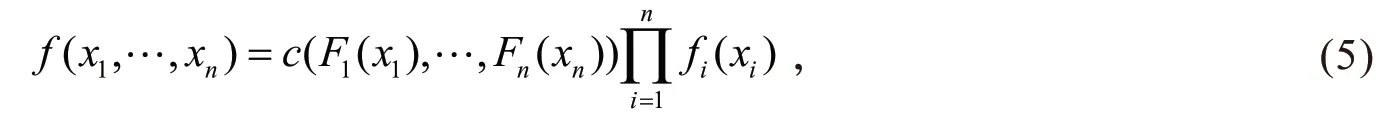
1.3.1 t-Copula函数

目前已经出现了多种Copula函数，可大致分为椭圆Copula和Archimidean Copula两大类，其中椭圆Copula函数根据随机变量所服从的具体分布可分为多元正态Copula和t-Copula。

由于金融数据的尖峰厚尾性，本研究将各板块的综合金融指数拟合成t分布，利用t-Copula函数进行组合资产的风险价值测量。t-Copula满足

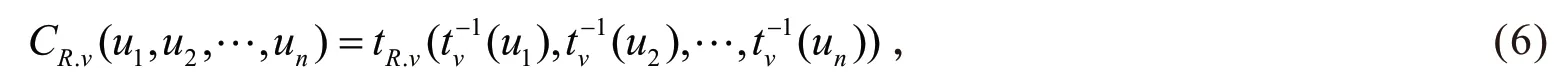
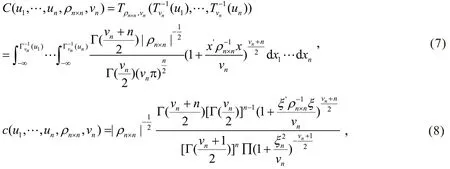
其中的参数可以由两阶段法的极大似然估计求出，即先估计出各边缘分布的参数，边缘分布确定后，代入数据进行（0，1）之间的映射则可得出累计分布的数据，再由映射后的数据得出Copula函数的参数。图1是参数为（0.5，3）的二元t-Copula函数的展示，从四角的分布情况可以看出其具有的厚尾特性，这表示极端值出现的可能大小[15]。

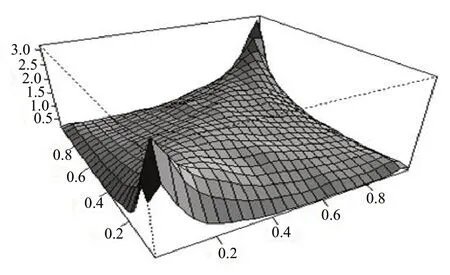
图1 二元t-Copula函数

1.3.2 CoVaR的计算

若X i和X j分别表示板块i和整个机构j的对数收益率序列，f(X i，X j)表示X i和X j的联合分布密度函数，则X j在既定的条件下分布密度函数为

将Copula函数与式(9)结合，便可得到

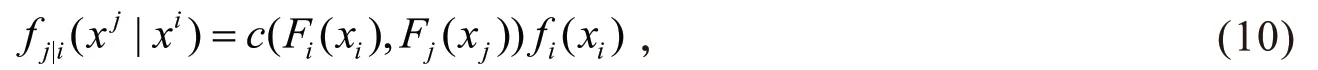
所以整个机构j的CoVaR值可以由下式得到

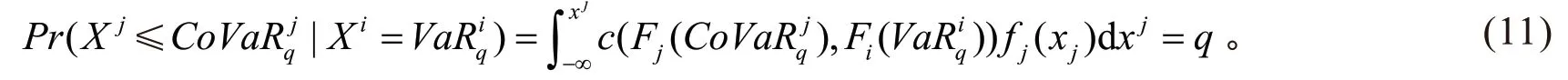
也就是说，在确定了分位数q、金融板块i的VaR值，就可以反解出的值，通过Fj函数的逆运算，就可以得出整个机构j的CoVaR值[16]。

2 实证分析

本研究选择中央汇金资产管理公司所投资的20只股票进行研究，数据来源于东方财富choice金融终端，为2015年6月1日至2021年3月23日的日收盘数据，去除缺失值后，数据数量为948个，股票名称及类别如表1所示。

表1 样本分类及名称

利用对数收益率公式

其中Pt表示第t天该股票的收盘价格，则可计算出每只股票的波动率，再进行k-均值聚类，将收益率相似的股票聚为一组，由此产生新的5个板块，如表2所示。

表2 聚类后样本分类情况

令每股的股本数为1，利用加权法计算出各板块(A-E)和总体的股票收益率F的综合指数[17]，给出图1所示对应的二维平面散点，如图2（a）所示；绘制出各板块和总体收益率映射之后的散点图，如图2（b-f）所示。

通过上述图像的比对，可以看到图2（b-f）的分布情况都与图2（a）具有极大相似性，并展现出不同程度的厚尾特征，所以选择二元t-Copula函数是合理的。现在将各数据拟合成t分布，计算出所有边缘分布函数的参数，再利用t-Copula函数进行连接，估计出5个t-Copula函数的参数(ρ,v)，结果如表3所示。

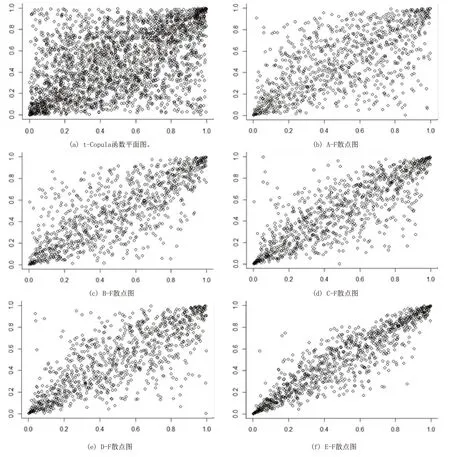
图2 散点图

表3 参数估计情况

根据上述Copula函数的参数估计结果，以及Copula函数自身定义域的特点，可采用Monte Carlo模拟计算各个板块的综合收益率对整个金融机构的风险贡献[18]，当各个板块的股票出现危机时，可以选用5%的分位点，相对应的机构收益率便是所求的CoVaR。第一步，随机生成满足上述t-Copula函数的两列1 000个属于(0,1)之间的概率序列；第二步，筛选出当5个板块处于5%的分位点时，整个机构的累计概率值；第三步，重复以上步骤10 000次。这样就能得到当某个板块处于风险和正常状态下整个机构的累积概率的分布情况，再取出5%分位点的累积概率值，通过边缘分布的逆运算得出相应的CoVaR，ΔCoVaR和ΔCoVaR/VaR值,结果如表4所示。

表4 计算结果及检验情况

从表4可以看出，各个股票板块的风险溢出虽然对整个投资机构的影响程度各有不同，但通过CoVaR方式测度出的系统性风险都要远大于用VaR测出的风险，出现这种情形的原因，是由于整个系统的综合股票收益率指数是由各个金融产品的收益率通过简单平均计算而来，所以各个板块的综合收益率与整个机构的综合收益率之间存在着从属关系，故当某个板块陷入风险时，对整个金融机构的系统性风险存在严重的影响。

其中第1、2、3、4个板块的溢出水平较高，都达到80%以上，管理者和投资者在进行整个机构的风险管理时应着重注意这4个板块；而第5个板块的风险溢出水平约有60%，是所有板块中溢出水平最低的一类，当该板块的股票陷入危机时，其对整个机构的溢出风险水平影响相对较小；但其中第3个板块的风险溢出水平最高，超过100%，所以应对迪马股份、中信重工、四方股份、中天科技、北方导航这几支股票尤为注意。

3 结论

本研究基于Adrian等提出的CoVaR理论，结合聚类分析和Copula函数，对中央汇金投资机构进行了系统性的风险测度，并且在进行整体风险管控时，从所持有股票对整个机构的风险溢出水平进行分析，指出了管理者应该着重监督管理的股票。这一方法增加了管理者对金融机构监管的灵活程度，对整个机构的风险管理不再采用笼统的一体化监管方法，而是可以根据机构本身所拥有的金融产品的风险溢出情况，对不同类型的股票进行有差别的灵活管控，为风险管理者提供了新的管控方向。