微细金属切削加工精度的有效提升方法研究

金红基，蒋永敏

（甘肃畜牧工程职业技术学院，甘肃 武威 733006）

1 微细金属切削加工精度优化方法设计

1.1 建立微细金属切削加工错位本构关系

本文在设计微细金属切削加工的精度优化方法时，采用了变形区应力的尺度切削效应机理，并通过应力变化的梯度分析获得了较为全面的理论阐述，作出了对尺度错位影响的预测。

因此在该模型中，错位材料的非均匀形变与应变梯度之间的关系可以表示为：

式中，γd表示非统计存储结构中的几何错位参数，即非均匀形变和应变梯度之间的集合本构关系参数；μm表示应变梯度；hL表示矢量结构。本构关系参数与剪切应力密度相关联，则可以得到：

式中，η表示微细金属剪切应力的错位密度函数；λ表示微细金属的剪切模量，一般取值为0.25；Ax表示几何错位的形变量。

通过公式（1）和公式（2）可以得到一个有关于尺度效应的详细解析，并对微细加工区域的变形分析起到良好的效果，将应变梯度应用在微细金属切削加工的本构关系中，可以为错位模型的建立提供良好的前提条件。并通过式（1）和式（2）统计出错位的密度函数：

式中，fρ(x)表示错位本构关系中的密度函数；Dref表示微细金属切削加工中拉伸轴的应变关系；f(a)表示均匀变形的梯度变化函数；Ax表示几何错位的形变量；bL表示微细金属切削实际位置与理想位置之间的间距，即误差值。通过以上公式，可以建立微细金属切削加工错位本构关系，并据此观察尺度函数中的加工效应。

1.2 计算切削区域应变梯度位移

通过微细金属切削加工区域的容错分析，可以得到几何模型的主形变单元位移量，并得到一个类平行四边形的结构，如图1所示。

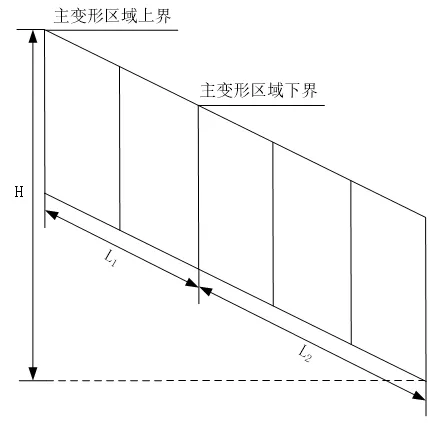
图1 切削区域应变梯度位移分析

如图1所示，在每一个平行四边形区域中，都有一个用于区分变形区的单元格，其长度为H，宽度为L，且主变形区域的上界共占有两个单元格，主变形区域的下界占有三个单元格。对于每一个长度单位为L的单元，切削加工的位移变化量可以通过公式（4）计算：

式中，Δgx表示从一个单元格转移到另一个单元格的过程中唯一变化量的长度单位；Li表示从第一个单元格转移到另一个单元格经过了i个单元格；H表示单元格的长度；Δi表示单元格的宽度单位。在经过正交切割理论之后，可以适当在主厚度边缘生成一个剪切应力，其前角的切割位移可以表示为：

式中，λx表示微细金属的主切割区域向周边位移产生的剪切型变量；Fs表示主切割刀对微细金属产生的剪切应力；Ty表示切割的位移长度。通过以上计算可以直接计算出应有的切割长度与方向。

1.3 建立微细金属切削加工精度优化模型

对于微细金属的切削加工精度优化模型，可以通过上文中的本构模型以及梯度位移形变量得到最常见的修正参数：

式中，σbg表示微细金属切削加工精度优化的修正参数；κ表示修正切削的本构材料系数；Hg表示各材料的单元长度；kj表示工件材料的塑形应变率；fa(x)表示宏观尺度下应变系数的错位函数。在引入修正参数的前提下，将应变函数与问题特性将宏观尺度相连接，就可以得到微细金属切削加工的精度优化模型，并以此提高金属加工的精度。

2 实验设计

2.1 实验准备

为了检测上文中细微金属切削加工精度提升方法的有效性，设计如下实验，将其与文献[1]、文献[2]中的两种精度优化方法进行对比，通过提升后的精度比较，判断三种方法的优劣，从而判断本文的方法是否得到了精度的优化。设置某细微金属的加工模型如图2所示。

图2 微细金属模型

如图2所示，将该微细金属模型以每0.01mm作为一个单位长度，在初始切削加工方法下，细微金属的原始精度如表1所示。

表1 细微金属切削加工初始精度

细微金属初始的切削加工精度及误差值如表1所示，为了测试三种方法是否能够降低误差，提高切削加工的精度，使用三种方法分别对该细微金属的模型进行切割，并记录十个目标位置中实际加工指标与理想加工指标的误差值。误差值越小，表明该精度提升方法越好。

2.2 实验结果分析

为了保证实验结果的准确性，对上述实验反复进行10次，记录每一次实验的数据，并计算其平均值如表2所示。

表2 误差值结果

如表2所示，在十个不同的位置中，三种精度提升方法均实现了误差值的降低，所有精度计算均高于初始结果。但是在三种精度提升方法的比较中，本文设计方法的误差平均值约为0.00582mm，文献[1]使用方法的误差平均值约为0.01447mm，文献[2]使用方法的误差平均值约为0.01274mm。通过数值的比较，可知文中方法的误差值更小，该细微金属切削加工精度方法对精度的提升更明显。

3 结语

在微细金属的切削加工中，经常会因为目标尺寸过小，而导致加工精度不足。因此本文设计了一种微细金属切削加工精度的有效提升方法，通过建立微细金属的本构关系，计算了理想尺寸位置与实际位置之间的关系。并设计实验，对比本文设计的精度优化方法与现有的两种优化方法之间的精度误差值，通过实际数据，证明了该优化方法的优越性。