Theoretical calculations of hyperfine splitting,Zeeman shifts,and isotope shifts of 27Al+and logical ions in Al+clocks∗

Xiao-Kang Tang(唐骁康), Xiang Zhang(张祥), Yong Shen(沈咏), and Hong-Xin Zou(邹宏新)

College of Liberal Arts and Sciences,National University of Defense Technology,Changsha 410073,China

Keywords: Zeeman effect,isotope shift,aluminum ion optical clock,MCDHF method

1. Introduction

Nowadays,the ultra-high precision optical clock systems have played an important role in the fields of metrology,satellite navigation,deep space exploration,very long baseline interference (VLBI), basic physical law inspection,etc. Especially for physics research,there are many characteristic applications,for example,the measurements on the temporal variation of the fine-structure constant and the proton-to-electron mass ratio,[1,2]the detections of relativistic effects such as time dilation,[3,4]gravitational red-shift,[5]and gravitational waves[6]as well as the search of dark matter.[7,8]

The uncertainty of the aluminum ion optical clock has now entered the order of 10−19,which is the lowest among all current optical clocks.[9]The27Al+optical clock adopts the weak allowed transitionJ=0→J=0. Compared with other atoms,it is less sensitive to the external magnetic and electric field, and is an ideal candidate for next generation frequency standard.[10]Since the wavelength of the electric dipole transition of27Al+is 167 nm,deep in the vacuum ultraviolet band,it is difficult to achieve direct laser cooling and quantum state detection. Therefore,sympathetic cooling and quantum logic spectroscopy are currently widely adopted.[11,12]

At present, the related theoretical calculations of27Al+,[16,17]9Be+,[18–22]and25Mg+[23–29]have been reported, but most of these works focused on a certain energy level or a certain physical constant of a particular ion. Moreover, different calculation methods lead to different results,and the impacts are difficult to evaluate. To solve this problem,we performed a comprehensive calculation under a similar framework for the transitions involved in the clock ion27Al+and its logical ions9Be+and25Mg+,which can provide some important theoretical parameters to further suppress the uncertainty of the27Al+optical clock.

In this paper, we calculate the hyperfine constants, Zeeman coefficients, and isotope shift parameters of related energy levels in these ions by employing the multiconfiguration Dirac–Hartree–Fock (MCDHF) method. The differences between the calculated values and the experimental values of the Zeeman coefficients are all below 0.34%.These results will be helpful to analyze and evaluate the uncertainty of the optical clock system. Especially when accurate experimental values are not available,these results could be used as alternative reference values. The calculated isotope shifts can provide important parameters for the spectroscopic experiment to measure the nuclear charge radii,and help to understand the structures,properties and nucleon interaction law of these three elements.

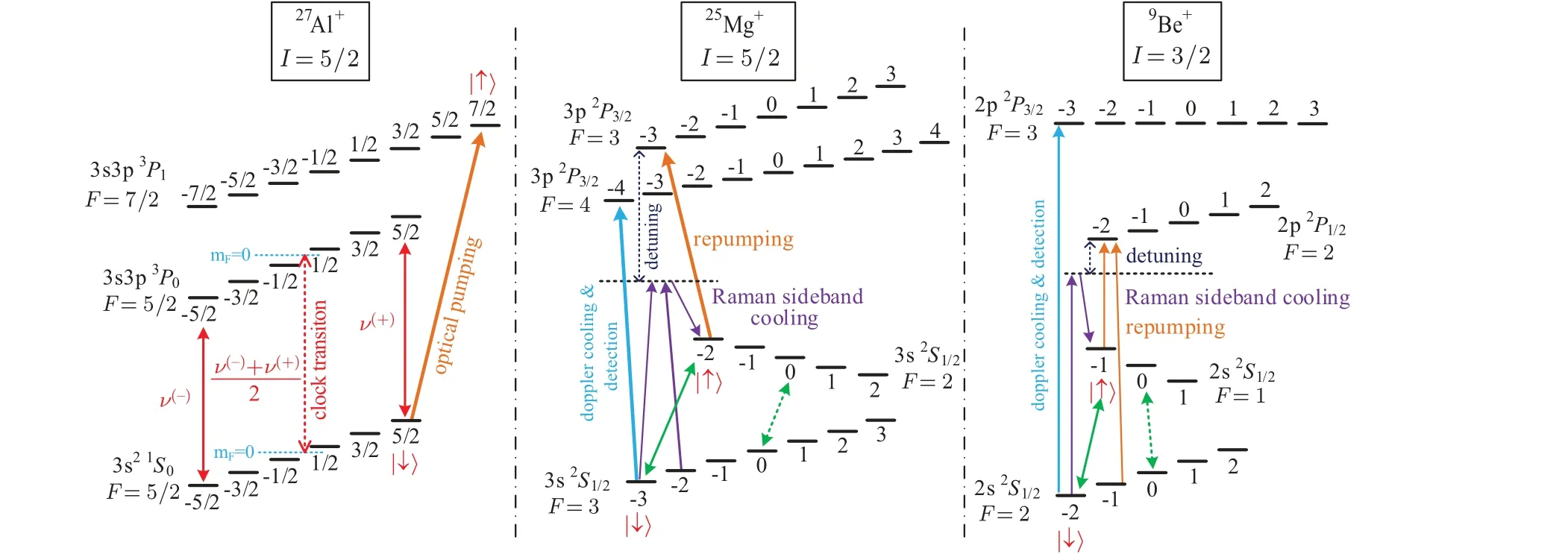
Fig.1. Energy levels and relevant transitions of 27Al+ and its logic ions 9Be+ and 25Mg+. The qubit states of an ion are denoted by|↑〉and|↓〉.

2. Theory and computational details

2.1. Calculation theory

The process and accuracy of atomic structure calculation strictly depend on the representation of atomic states and the explicit definition of many-electron basis. In the MCDHF method, the atomic state wave functions (ASFs) are the linear combination of configuration state wave functions(CSFs)with the same parityP, total angular momentumJ,and itszaxis componentMJ,[30]

wherenis the principal number andκis the relativistic angular number.Pnκ(r)andQnκ(r)are the large and small component radial wave functions andχκm(θ,ϕ) is the spinor spherical harmonics. In the self-consistent field (SCF) process, using the variational method, the CSFs and the corresponding mixing coefficients are optimized by iteratively solving the equations. The calculation of ASFs is completed by GRASP2K package.[31]

When the nuclear spinI/=0, the electrons and the electromagnetic multipole moments of the nucleus will interact to produce the hyperfine structure of an atomic energy level. The corresponding Hamiltonian may be represented as a multipole expansion[32]

Here,T(k)andM(k)are spherical tensor operators of rankkin the spaces of electronic wavefunctions,|γJMJ〉and nuclear wavefunctions|ν|M1|〉respectively. Thek=1 term of the expansion represents the magnetic dipole interaction and thek=2 term the electric quadrupole interaction. Higher order terms are tiny and can often be neglected. The magnetic multipole tensors are

Here,iis the imaginary unit,αis the fine-structure constant,αis the Dirac matrixs, andC(k)is thek-th order spherical tensor. Usually,the hyperfine splitting is considered independently for each atomic level and without the need to specify all the hyperfine level energies explicitly. Instead,with the nuclear magnetic dipole momentµIand electric quadrupole momentQ,the energy splitting of an atomic level into hyperfine levels can be expressed conveniently in terms of the hyperfine interaction constants[33,34]

withC=F(F+1)−J(J+1)−I(I+1) where the total angular momentumFis formed by the coupling of the nuclearIand electronicJangular momenta.

In addition to the hyperfine splitting caused by the coupling of electron spin and nucleus spin,the external magnetic field can split the energy level further. Neglecting diamagnetic contributions and the interaction of the magnetic field with the nucleus, and choosing the direction of the external magnetic field as thezdirection, the magnetic (Zeeman) Hamiltonian can be written in terms of spherical tensors[35]

Here,Bis the magnetic field and the second term in the magnetic Hamiltonian above is(so-called)Schwinger’s QED correction. For anN-electron atom, the electronic tensor operators are

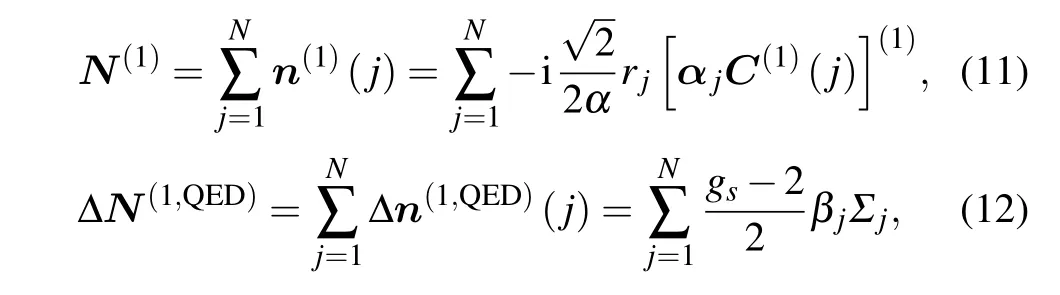
whereΣjis the relativistic spin-matrix, andgs=2.00232 is theg-factor of the electron spin. Wave functions for magnetic hyperfine structure substrates in an external magnetic field are expanded in a basis of the combined nuclear and atomic system[36]

In the calculation process,the reduced hyperfine and Zeeman matrix elements are used to construct the total interaction matrix in the given basis.By diagonalizing the interaction matrix,the Zeeman energy splittings of hyperfine structure substates are obtained together with the expansion coefficients of the basis functions. The hyperfine interaction constants and Zeeman splittings are obtained by the HFSZEEMAN module.[32]

The real atomic nucleus is a finite quantum system with a certain mass composed of protons and neutrons,and its charge distribution can be described by the nuclear root-mean-square charge radius. The energy shifts between spectrum lines of different isotopes are called isotope shifts(ISs),which consist of the mass shifts(MSs)due to the finite and different masses of the isotopes considered and the field shifts(FSs)caused by differences in the nuclear charge distributions of the isotopes.The isotope shift of a given transition between two isotopes,AandA′,with nuclear massesMandM′,is written as[25,37,38]

Here,the first term called MS is the sum of two contributions:the normal mass shift (NMS) parameter ∆KNMSand the specific mass shift (SMS) parameter ∆KSMS. The second term called FS is the product of the field shift parameter ∆Fand the termδ〈r2〉the difference of the nuclear mean-square charge radii between two isotopes.[39]The calculations of the isotope shifts are performed by the RIS module.[40]

For the nuclei with charge numberZand massM,the MS Hamiltonian under the(αZ)4m2/Mapproximation is

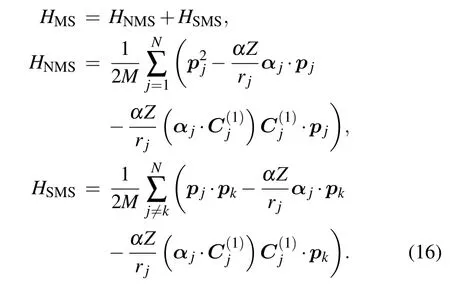
Here,pis the momentum operator of the electron andmis the mass of the electron. The NMS parameterKNMSand the SMS parameterKSMSof a given level are defined by the following expressions,respectively,

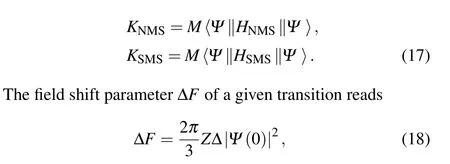
proportional to the change of the total probability densityρ(0)at the origin

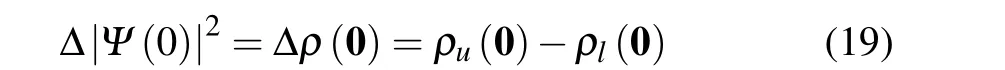
associated with the transition between levelslandu.

2.2. Calculation models

To obtain higher calculation accuracy, it is usually necessary to capture the electron correlation sufficiently and appropriately. The active space approach is employed to systematically capture the electron correlation.[41]The reference configurations of27Al+are 3s21S0,3s3p3P1,0,and 3s3p1P1.The reference configurations of25Mg+are 3s2S1/2and 3p2P1/2,3/2. The reference configurations of9Be+is 1s22s2S1/2and 1s22p2P1/2,3/2. The calculations were carried out by parity,meaning that the even and odd states of a single ion were optimized in separate SCF processes. During the calculation,the occupied orbitals 1s, 2s, and 2p of27Al+and25Mg+and 1s of9Be+are treated as core orbitals, and the others as valence orbitals. The electron correlation can be divided into first-order and high-order correlations, the former is captured by the CSFs generated through the single(S)and double(D)substitutions from the occupied orbitals in the single reference configuration set. In particular,the CSFs of27Al+and25Mg+are generated by single and restricted double (SrD) substitutions from core and valence orbitals, limiting the excitations to a maximum of one hole in the core. To describe the electron correlations,the first-order correlation is further separated into the correlation between the valence electrons(VV correlation),the correlation between valence and core electrons(CV correlation), and the correlation between core electrons (CC correlation). For27Al+and25Mg+ions,only the CV and VV correlations are taken into account, while for9Be+, all three correlations are considered.

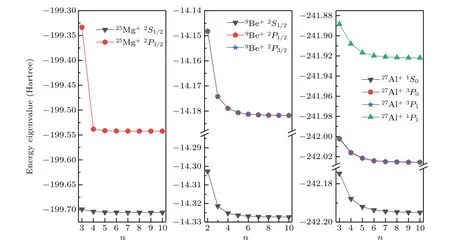
Fig.2. Variations of the energy eigenvalues(in unit Hartree,1 Hartree=27.2114 eV)of the related energy levels in 27Al+, 9Be+,and 25Mg+ions along the calculation layer n. The abscissa n is the maximum quantum number of the active orbitals in the corresponding layer.

The orbital optimization in variational methods is achieved through an iterative process that requires initial estimates. Many difficulties can be avoided by adopting a systematic procedure where, instead of a large-scale calculation with many orthogonality constraints,a series of smaller calculations are performed with larger and larger orbital sets and the results from one are part of the input for the next. The maximum principal quantum numbernof the active orbitals starts from two or three for the first layer and only increases by one per layer until it equals ten,and the angular quantum numberlis set to the maximum by default. But in the test calculation, we found that some active orbitals with largel(such as 7i,8i,9i orbitals,etc.) had little contribution to the results and took up too many computing resources to slow down the overall computing speed. Therefore, these orbitals are not taken into account in this paper.In addition,the orbital sets of27Al+formed in the layern=10 were fixed in subsequent relativistic configuration interaction (RCI) calculations in which the CSFs through single, double, and triple (SDT) substitutions from the reference configurations to orbitals within 5s,5p,4d,and 4f were included.

Figure 2 shows the variation trends of the energy eigenvalues of the corresponding states in27Al+,9Be+,and25Mg+ions along the calculation layers. As the number of configuration layers increases, the eigenvalue of each energy level gradually decreases and shows a convergence trend.

3. Results and discussions

Because the nuclear spins of27Al+,9Be+, and25Mg+ions are not zero, their energy levels with non-zero angular momentumJhave hyperfine structures whose precise measurements are essential parts in the optical clock experiment.The hyperfine interaction constants of the related energy levels are given in Table 1. Our calculation model of Al+ion is similar to the one in Ref.[16],so the differences of the hyperfine interaction constants of the 3s3p1P1state are within 0.6%.Since the high-order electron correlations and CC correlations are not considered, there is a big difference in the hyperfine interaction constants of the 3s3p3P1state. The uncertainty estimation method given in Refs. [47,48] is used to derive the uncertainty of the hyperfine interaction constants in Table 1.

By comparing the values in Table 1,we find that our magnetic dipole constants of 2s2S1/2and 2p2P1/2states of Be+are in good agreement with the experimental values,while the magnetic dipole constants of 3s2S1/2state of Mg+is 3.6%higher than the experimental values. The reason why it is not as good as that in Ref. [24] may be that the main electron correlations in the calculation model of Mg+ion are less complete. The maximum differences between the hyperfine structure constants of 3p2P1/2and 3p2P3/2states of Mg+and others’theoretical values are 7.3%and 9.5%,respectively.For the magnetic dipole constant of the 2p2P3/2state of Be+,the ratio of the uncertainty to the calculated value is 0.278. This is because there is no obvious linear relationship between the differences of the calculated values and the differences of the energy eigenvalues,so it is not suitable for the uncertainty estimation by the method given in Refs.[47,48].

Table 1. The hyperfine interaction constants of the related energy levels in 27Al+, 9Be+,and 25Mg+ ions. A is the magnetic dipole constant(in unit MHz).B is the electric quadrupole constant(in unit MHz).

Fig.3. The Zeeman shifts of the 3P0 and 3P1 states in 27Al+ as functions of the magnetic field B. Splitting energy E is the Zeeman splitting value, and ∂E/∂B is the partial derivative of splitting energy E with respect to magnetic field B. Different curves correspond to Zeeman sublevels with different mF values.

The Zeeman splitting of the2S1/2state in25Mg+along the magnetic field is given in Fig. 4. The Zeeman shifts of the|3,±3〉sublevels in Figs.4(a)and 4(b)are approximately linear when the magnetic field strength is in the range of 0–2000 mT,and the linear coefficients are−1.4012 GHz/T and 1.4012 GHz/T, respectively. We can find a significant transition from low field,whereIandJare coupled to form the total angular momentumF, to high field, where they are decoupled. When the magnetic field strength is close to 2000 mT,the Zeeman shift of each sublevel begins to change linearly and approach the linear coefficients of the|3,±3〉sublevels.

For the|3,0〉→|2,0〉transition in Fig. 4, the quadratic Zeeman coefficients of these two sublevels are opposite in sign and equal in magnitude,that is,the sum of them is always near zero. Therefore, the high-order Zeeman effect of this transition is small compare to the ones of other transitions and can be used to measure the ground-state hyperfine interaction constant.[46]This transition is also second-order sensitive to the external magnetic field and is used to determine〈B2〉.[14]For the|3,−3〉→|2,−2〉transition,the lower level|3,−3〉has only the first-order Zeeman effect,and the upper level|2,−2〉has the weakest second-order Zeeman effect in the splitting of the levelF=2, so this transition is first-order sensitive to the external magnetic field and is used to determine the DC component of〈B2〉in real-time.[14]4, 3)state in25Mg+in the magnetic feild, and the decou-

Fig.4.The Zeeman shifts of the2S1/2 state in25Mg+as functions of the magnetic field B. Splitting energy E is the Zeeman splitting value,and ∂E/∂B is the partial derivative of splitting energy E with respect to magnetic field B.Different curves correspond to Zeeman sublevels with different|F,mF〉.

Fig.5. The Zeeman shifts of the 2P3/2(F=4,3)state in 25Mg+as functions of the magnetic field B. Splitting energy E is the Zeeman splitting value,and∂E/∂B is the partial derivative of splitting energy E with respect to magnetic field B. Different curves correspond to Zeeman sublevels with different|F,mF〉.

Figure 5 showsthe Zeeman splittingof the2P3/2(F=pling of angular momentums in high magnetic feild is more complicated than that in Fig. 4. When the magnetic feild strength increases to about 20 mT, the curves of sublevels split fromF=4 andF=3 levels intersect. Once the magnetic field strength exceeds 90 mT, the Zeeman shifts of all sublevels tend to change linearly. The linear coefficients of the|4,±4〉levels at the top and bottom edges of Fig. 5(b)are±2.800755 GHz/T,respectively. When the magnetic field strength is within 10 mT,these energy sublevels mainly show the first-order and second-order Zeeman effects.

The Zeeman splitting of the2S1/2state of9Be+along the magnetic field in Fig. 6 is similar to that of25Mg+in Fig. 4.When the magnetic field strength is more than 1500 mT, the Zeeman shifts of the sublevels in9Be+show linear trends,and the change rates along the magnetic field begin to get closer to those of|2,±2〉levels. The linear coefficients of the|2,±2〉levels are±1.40122 GHz/T, respectively, with 0.02 MHz/T deviations from the linear coefficients of the|2,±2〉sublevels of the2S1/2state in25Mg+.

Among the sublevels that intersect the vertical axis in Fig. 6(c), only the|2,0〉and|1,0〉sublevels are symmetric about∂E/∂B=0,and the sum of the Zeeman coefficients of these two sublevels is always 309.49963 MHz instead of the case in25Mg+where the sum is zero. Therefore,the secondorder Zeeman effects of the|2,0〉→|1,0〉transition cancel out,and this transition is generally used to study the first-order Zeeman effects. The|2,−2〉sublevel only has first-order effect,the Zeeman effects above second order of the|1,−1〉sublevel are weak, and both are at the outermost side of the sublevels split from the same level. In consequence, these two transitions are generally measured experimentally to study the effect of the magnetic field on the energy level structure of the2S1/2state in9Be+.Besides,the|2,−2〉and|2,2〉sublevels of the2P1/2state in9Be+have second-order Zeeman effects that are small compared to other sublevels,so it is not easy to observe directly from Figs.6(b)and 6(d). Based on the calculation data,we obtain that the first-order coefficients of|2,2〉and|2,−2〉sublevels in9Be+are±0.46574 GHz/T, respectively,and the second-order coefficients are−1.53333 MHz/T2and−1.53286 MHz/T2,respectively.

Figure 7 shows the Zeeman shifts of the2P3/2states in9Be+as functions of the magnetic field. When in the high magnetic field, due to the decoupling of the angular momentums, the sixteen curves of the sublevels of the2P3/2states in Fig. 7(a) can be evenly divided into four groups according tomJ,with four curves in each group tending to be linear and roughly parallel. Specifically, the first-order coefficients of the|3,−3〉,|3,−2〉,|3,−1〉,and|3,0〉sublevels in the first group are all−2.80078 GHz/T, the first-order coefficients of the|2,−2〉,|2,−1〉,|2,0〉, and|3,1〉sublevels in the second group are all−0.931 GHz/T,the first-order coefficients of the|1,−1〉,|1,0〉,|2,1〉,and|3,2〉sublevels in the third group are all 0.936 GHz/T, and the first-order coefficients of the|0,0〉,|1,1〉,|2,2〉, and|3,3〉sublevels in the fourth group are all 2.80078 GHz/T. These linear coefficients are only applicable in the magnetic field above 400 mT,and the linear coefficients of the outer sublevels have more precise digits. Especially for the first and fourth groups,the coefficients are equal in magnitude. Among these sublevels,the outermost|3,±3〉sublevels often considered in experiments mainly have the first-order Zeeman effects.

Fig.6. The Zeeman shifts of the 2S1/2 and 2P1/2 states in 9Be+ as functions of the magnetic field B. Splitting energy E is the Zeeman splitting value, and ∂E/∂B is the partial derivative of splitting energy E with respect to magnetic field B. Different curves correspond to Zeeman sublevels with different|F,mF〉.

Fig.7.The Zeeman shifts of the2P3/2 states in9Be+as functions of the magnetic field B. Splitting energy E is the Zeeman splitting value,and ∂E/∂B is the partial derivative of splitting energy E with respect to magnetic field B.Different curves correspond to Zeeman sublevels with different|F,mF〉.

From the Zeeman splittings in Figs.3–7,we can see that the Zeeman energies of themF=±Fstates in which theFis the maximumFvalue for a reference configuration change linearly with increasingBfor all field strengths because their wavefunctions are not mixed. For other states, the magnetic effect tends to be first-order asBincreases in the high-field regime. This is because theIandJare decoupled and the Zeeman interaction dominates when the magnetic field is very strong,the eigenstates are well described by the|I,mI;J,mJ〉basis.

In addition to the hyperfine interaction constants and Zeeman shifts of the related levels in27Al+,9Be+, and25Mg+ions, we also calculate the isotope shift parameters of these levels, and the results are shown in Table 2. Compared with the theoretical values in Ref. [16], the deviations of ∆KNMS,∆KSMS, and ∆Fof the1S0→3P1transition in27Al+are 2%,1.8%,and 2.5%,respectively.However,the SMS parameter of the1S0→1P1transition in27Al+is quite different from that in Ref.[16],it is mainly because the SMS parameter is sensitive to the electron correlation,and the captures of the CC correlations and high-order correlations make the results different.

Table 2. The normal mass shift parameters KNMS (in unit GHz·u),the specific mass shift parameters KSMS (in unit GHz·u),and the field shift parameters F (in unit a.u.) of the related energy levels in Al+, Be+, and Mg+ions.

Table 3. Comparison of our theoretical predictions with the experimental results of isotope shifts of D1 and D2 lines for different Mg+ or Be+ isotope pairs. The D1 line and the D2 line of Mg+ correspond to the 3s 2S1/2 →3p 2P1/2 transition and 3s 2S1/2 →3p 2P3/2 transition,respectively. The D1 line and the D2 line of Be+ correspond to the 2s 2S1/2 →2p 2P1/2 transition and the 2s 2S1/2 →2p 2P3/2 transition,respectively. All values are given in unit MHz.

Currently, there is no experimental data on the isotope shifts of these transitions in27Al+for assessing the advantages of the calculation models. The experimental and theoretical isotope shifts of the D1 and D2 lines in Be+and Mg+ions are given in Table 3, and a good agreement between the experimental results and our calculation results is obtained. The calculation errors for the isotope shifts of Mg+and Be+ions are less than 1.3%and 0.07%,respectively,indicating that our calculation model is reliable.Table 3 shows that the uncertainties of isotope shifts of Be+are relatively large and the ratios of the uncertainties to calculated values are about 0.048.However,the differences between the calculated results of Be+and the experimental values are below 0.07%, which is closer to the experimental values than that of Mg+. This is becauseδKorδFand the difference of energy eigenvalues do not show a close to linear correlation,i.e., the linear uncertainty estimation method[47,48]is not suitable for the current calculation model of Be+ion.

4. Conclusion

In this paper, we use the MCDHF method to calculate the hyperfine interaction constants,Zeeman shifts,and isotope shifts of the states in27Al+ion and logic ions9Be+and25Mg+that are involved in the27Al+optical clock.We analyze the influence of the external magnetic field on these hyperfine structure energy levels, and the Zeeman shifts are given. These results will be helpful for better evaluation of systematic uncertainty of the27Al+optical clock.The calculation of isotope shift parameters can provide important reference data for the spectroscopic measurement of nuclear charge radius which is a necessary theoretical basis to study the structures,properties and nucleon interaction law of these three elements.