Modeling and dynamics of double Hindmarsh–Rose neuron with memristor-based magnetic coupling and time delay∗

Guoyuan Qi(齐国元) and Zimou Wang(王子谋)

Tianjin Key Laboratory of Intelligent Control of Electrical Equimpment,Tiangong University,Tianjin 300387,China

Keywords: bi-Hindmarsh and Rose(HR)neuron model,memristor,magnetic coupling,time delay

1. Introduction

The nervous system is a complex nonlinear dynamic system,and the human brain nervous system is composed of hundreds of billions of neurons. The coding and processing of information are closely related to the nervous system’s different firing patterns.[1]For example, periodic spiking and bursting states have different effects on information transmission.[2,3]The firing patterns in the neural model will be affected by many factors, such as connection methods between neurons,system parameters, time delays,etc.[4–7]Various neurological diseases are often related to the abnormal firing patterns of nerves.[8]Therefore, improving the neuron model according to the actual biophysical environment and studying its firing pattern[9,10]are extremely important for understanding brain activity and neural behavior.

To describe the nervous system vividly, scholars have proposed various types of mathematical neuron models based on the biological characteristics of neurons since the middle of the 20th century. In 1952, Hodgkin and Huxley proposed the famous Hodgkin–Huxley (HH) neuron model,[11]which laid the foundation for neuroscience. In 1961, FizHugh simplified the HH model, proposed the FHN model, introduced restoration variables, and reduced the HH model to two dimensions.[12]Hindmarsh and Rose proposed the Hindmarsh–Rose neuron model based on the FHN model,[13–15]which is regarded as an idealist by many scholars in the study of neuron firing.

The essential factors impacting the neuron firing patterns are the magnetic field,external stimuli,coupling mode of neurons,and time delay. Therefore,they are the critical elements in modeling the neuron or neural networks.

Recent studies have proposed that the electrical activity of neurons may be affected by electromagnetic radiation. It has been found that there is a complex electromagnetic field in the nervous system and has a certain amount of energy consumption. Chua proposed the memristor concept in 1971,[16]which is a circuit element with the characteristics of memory resistance and a device representing the differential relationship between magnetic flux and electric charge. The memristor is used in various academic fields, and it is reasonable to use it to describe the electromagnetic induction effect in neurons. Many scholars have regarded electromagnetic induction and electromagnetic radiation as crucial physical factors for constructing neuron models[2,17–21]Lv and Ma[22]found that fluctuations in neuron membrane potential can change the distribution of electromagnetic fields inside and outside neurons and used memristors to represent the effect of time-varying magnetic fields on neuron firing patterns. In 2019, Baoet al.[23]used a memristor to describe the electromagnetic induction phenomenon caused by ions’ movement across the membrane. They found that the electromagnetic induction phenomenon can induce multiple firing patterns of neurons.Linet al.[18,24]investigated the effects of external electromagnetic radiation on the chaotic dynamics of the Hopfield neural network with three neurons. Hidden chaotic attractors and hidden hyperchaotic attractors were also observed in the neural network. Linet al.[25]proposed a model of locally active memory neurons, having the characteristics of multiple firing modes coexisting. Ren,Lvet al.[26,27]found that magnetron memristive neurons switch in multiple firing modes under external stimuli and synaptic cooperation. Memristors can not only describe the electromagnetic induction caused by the time-varying magnetic field in the electrophysiological environment inside and outside the neuron cell membrane,but also have the potential to reproduce the behavior of a biological synapse.[28–30]

The coupling part must be described for two connected neurons. It influences the firing pattern,and the memristor can also describe the communication between neurons and various brain regions under electromagnetic field coupling.[4,6,31–38]A neural model coupling two two-dimensional(2D)HR neurons based on an active memristor was recently established.[31]Maet al.[32]studied magnetic flux coupling-induced complete phase synchronization behavior based on magnetron memristive neurons. Ushaet al.[35]analyzed the effects of coupling strength and external stimulus on the synchronous state of neurons from the perspective of energy. Xuet al.[36]studied the phase synchronization of two neurons under magnetic field coupling and the influence of noise on synchronization stability. In Ref. [4] a bi-neuron network model of memristor was established;memristor is used to describe the electromagnetic induction caused by the potential difference between adjacent neuronal membranes and the coexisting firing activity in dual neural networks was studied. Similar issues were also discussed by Baoet al.,[5,38]in which the coexistence behavior of multiple firing modes in two adjacent neurons under the coupling of magnetic fields was found. The above results show that the coupling mode of neurons, magnetic field, and external stimuli all have a non-negligible effect on neurons’firing patterns. In previous studies, scholars typically describe the electromagnetic induction effect between neurons from the perspective of adjacent neuron membrane potential differences. Few references have studied the coupling phenomenon based on the magnetic field from the perspective of the magnetic field generated by the neurons themselves. We found that the coupling magnetic field significantly influences the dynamics and firing pattern of the connected neurons.Therefore,it is necessary to consider the coupling part in modeling and dynamical analysis.

Due to the limitation of signal transmission speed and the lag of transmitter release,the time delay is inevitable in neural networks. Existing studies have shown that the time delay in the coupling process will significantly affect the system’s stability and dynamic synchronization mode.[39–42]The analysis of clinical data based on neuro medicine confirmed that time delay is also one of the complex dynamic mechanisms of the occurrence and development of mental illness.[43–45]Qinet al.[39]described the effect of autapse on neurons by introducing a time-delayed forced current on the membrane potential with a certain gain.It was found that neurons are driven to produce spikes, bursts, and chaotic activities by slightly increasing feedback gain and time delay. Hanet al.[40]investigated the effect of synaptic delay on the synchronization robustness of neural networks. Steuret al.[42]studied the coupled HR neural networks,the time delay representing adjacent neurons’membrane potential signals in the previous period. Huanget al.[43]studied the time-delay coupling HR neural network in a similar approach and found that appropriate time delays can trigger mode conversion and step synchronization behavior of coupling neural networks. In previous studies, there were rarely considered time lag during the coupling process of the magnetic field. We found that the time lag in the magnetic coupling process impacts the ability of neurons to respond to external stimuli and coupled magnetic fields.

It is necessary to optimize the memristive neural network model further to make the neuron model closer to the real cell environment and explore the internal relationship between the dynamic behavior of the memristor coupled neuron system and the coupling mode and time delay. This paper proposes a new time-delayed electromagnetic field coupled dual Hindmarsh–Rose neuron network model(Bi-HR).

The contributions of this paper are as follows:

(i)In modeling Bi-HR,the magnetic field-based coupling is provided using memristors.

(ii) The effect of coupled magnetic field on the firing of the neuron model can activate the static neurons in the neural network and produce complex discharge phenomena.

(iii) It is found that the time delay phenomenon in the magnetic coupling process can make the neurons have a powerful response-ability to external stimuli to maintain the normal firing state.

The rest of this article is organized as follows: In Section 2, the time-delay memristive dual neuron model with coupled memristive electromagnetic induction is built and the model’s rationality is analyzed.Section 3 studies the magnetic coupling phenomenon and the influence of time-delay on neuron firing patterns through sub-illustrations, dual-parameter sub-illustrations and firing timing diagrams. Conclusions are given in Section 4.

2. Modeling of Bi-HR neuron model with time delay based on memristor magnetic coupling

The difference in ion concentration inside and outside cell membrane is the main reason for maintaining membrane potential.However,the continuous transmembrane movement of charged ions will cause complex fluctuations in the ion concentration inside and outside the membrane, thereby generating a time-varying electromagnetic field. The electromagnetic induction effect can change the electrophysiological environment inside and outside the cell membrane and affect neurons’electrical activitys.

In 2016, Maet al.[22]proposed a classic HR neuron model with memristor based on the Hindmarsh–Rose model.The influence of electromagnetic induction on neuron membrane potential was considered. The improved model is defined as

wherexdescribes the membrane potential;yis recovery variable;zis adaption current;ϕrepresents the magnetic flux across the membrane of a neuron;Iextis external forcing current;m1W(ϕ)xdefines the feedback current at the membrane potential as the magnetic flux changes,andm1is the feedback gain;a,b,c,d,r,s,m,m2are system parameters,αandβare inner parameters of the memristor emulator.

Equation (1) is the model describing the single neuron,which cannot exist in a real neural environment because the natural neural network must consist of numerous neurons.However, modeling the neural network with many neurons is challenging work and complicated. Therefore,modeling a bineuron system is practical and significant.

In 2019,Baoet al.proposed a 5-dimensional dual-neuron model.[38]This model is a two-dimensional Hindmarsh–Rose model connected by a threshold memristor, and the memristor used to represent the electromagnetically induced current when two adjacent neurons had membrane potential differences,which is described as

wherex1,y1, andx2,y2represent two adjacent neurons;ϕis the inner magnetic flux;the termmtanh(ϕ)(x1−x2)represents the electromagnetically induced current between two neurons caused by the membrane potential difference;mrepresents the coupling strength of the memristor electromagnetic induction effect. However, the external forcing current, the time delay,and the self-feedback magnetic field in the coupling process are not considered in the model. These parts exist in the natural cell environment and will affect the firing of neurons. It can be seen from the last sub-equation in Eq.(2)that the magnetic field is generated by the membrane potential difference between two adjacent neurons.

We propose a Bi-HR neuronal model of magnetic coupling of memristive synapses with time delays. The memristors describe the phenomenon of neuronal membrane potential coupling based on magnetic fields, and the electromagnetic fields are generated by the continuous movement of ions across membranes. The proposed model of the Bi-HR neuronal network is

where the adjacent neurons described byx1,y1andx2,y2;Iextis external forcing current;andIm1,Im2define the induced currents generated by coupling magnetic field and self-feedback magnetic field. A flux-controlled memristor represents the magnetic field.

In this context,the quadratic flux-controlled memristor is often used to simulate the electromagnetic induction effect,[22]but the parameters of the memristor model are relatively complex. So we seek a memristor model that is more in line with the characteristics of biological signals and has a simple expression. A simple threshold flux-controlled memristor is often expressed as

The hyperbolic tangent function is a monotone continuous differential function, often used as a neuron activation function bounded above and below in the Hopfield and BP neural network.[17]HerexandIrepresent the membrane potential and current at the input port of the memristor emulator,respectively,ϕrepresents the magnetic flux across the membrane of a neuron,iandjare two inner positive constants of the memristor emulator. The term(i−jtanh(ϕ))xdefines the feedback current of the membrane potential when the magnetic flux changes.

The question is how to express the coupling magnetic field? In this article, we extend this single threshold fluxcontrolled memristor of the Bi-HR model. We add a hyperbolic tangent function to Eq. (4) to represent the coupled magnetic field generated by neighboring neurons,which is expressed as

where the variableϕ1,ϕ2is the magnetic flux indicating the time integral of the membrane potentialx1,x2; the term(i−j·tanh(ϕ1)+k·tanh(ϕ2))x1defines the feedback current of the membrane potential when the magnetic flux changes;the termk·tanh(ϕ2) is defined as the rate of charge change caused by the coupled magnetic field generated by adjacent neurons;i,j,kare the internal parameters of the memristor,jrepresents the self-feedback strength of the neuron,andkis the strength of magnetic coupling between two adjacent neurons.

In the proposed BI-HR neuron model of Eqs.(3)and(5),the coupling magnetic field is generated by the change of the membrane potential of the neuron itself. In contrast,the magnetic field in Eq. (2) proposed by Baoet al.[38]and Xuet al.[36]is generated by the membrane potential difference between two adjacent neurons. Besides, the magnetic fields in the proposed model include the self-feedback magnetic field and the coupled magnetic field to the adjacent neurons.

3. Results and discussion

Since the concept of neural dynamics was put forward,the dynamic theories and methods to study cognition and nervous system activities have become the mainstream research method. The membrane potential of neurons has many firing patterns,which contain much crucial coded information. This paper investigates the Bi-HR neuron network of Eqs. (3) and(5),and reveals the transition of firing pattern closer to the natural biological and physical environment concerning the magnetic field and time delay, which is of great significance for exploring the information transmission and the prevention of neurological diseases.

For numerical studies,timeseries diagram,bifurcation diagram and bifurcation of the bi-parameter diagram are used to analyze the firing pattern and the trend of the Bi-HR neurons firing pattern transition.The parameters are selected asa1=1,b1=3,c1=1,d1=5,a2=1,b2=2.86,c2=1,d2=5.05,i=1.5,j=3.8.The fourth Runge–Kutta algorithm is used to calculate the nonlinear equations with time delays,and initial values for the variables are selected as(0,0,0,0,0,0). Another numerical algorithm can also be selected,like Dormand–Prince. We found that there is a tiny slight difference about 10−8between the two algorithms for the sampling time of 10−4,but this difference does not influence on the determination of the dynamical modes,like the sink,periodic orbit and chaos. The sampling time must be sufficiently short according to the Shannon theorem. We found that a tiny difference will be signified for the chaotic mode after a long time running from our calculation. However,the chaotic property and the bound have not been changed.

3.1. The influence of coupled magnetic field on membrane potential

In this part,we first study the influence of magnetic coupling intensitykon the membrane potential of neurons, and show the rich excitation patterns of neurons under different coupling intensities. To show dynamic behaviors in Bi-HR neurons model coupled by magnetic field intuitively, the bifurcation diagram of two parameters through the periodicity of membrane potentialxis shown in Fig. 1, where the initial parameters of memristori=1.5,j=3.8,τ=0 are assigned.It shows two dynamic behaviors: the periodic firing, marked in blue in Fig.1, the aperiodic firing, marked in other colors.The color bars represent the number of firing periods in a simulation of 5000 s. With the increasing number of periods,the color transits from blue to yellow. It can be seen in Fig. 1 that there is a clear boundary between the magnetic coupling phenomenon (k/=0) and non-magnetic coupling (k=0) of adjacent neurons. Whenk=0, the magnetic coupling phenomenon is not considered,the system presents a periodic discharge in the range of external stimulation currentIext∈(0,5).Once the value ofkis changed,the membrane potential jumps form periodic motion to chaotic behavior. The Bi-HR system produces abundant dynamical behaviors by introducing magnetic coupling.

Fig.1.Bi-parameter bifurcation diagram in Iext–k(external stimulus current–coupling strength),where the color indicates the number of firing periods in the simulation time,the blue and yellow parts representing periodic firing and non-periodic firing,respectively.

We study the changes of firing patterns after the neuron model introduces the magnetic field and magnetic coupling,as shown in Figs. 2(a) and 2(b). Select the parameters of the neuron model asa=0.86,j=3.8,k=1,Iext=3. The membrane potentialxis at the resting state without considering the coupled and self-feedback magnetic field. At 1000 s, after the neuron model is added a time-varying self-feedback magnetic field,i.e., in Eq. (5)Im1= (i−j·tanh(ϕ1))x1,Im2=(i−j·tanh(ϕ2))x2, the firing pattern changes to periodic bursting firings. At 2000 s,when the coupling magnetic field is also added,i.e.,Im1= (i−j·tanh(ϕ1)+k·tanh(ϕ2))x1,Im2=(i−j·tanh(ϕ2)+k·tanh(ϕ1))x2,the complete form of Eq. (4), and the parameters of the neuron model asa=0.86,j=3.8,k=1,Iext=3, the neuronal firing pattern becomes chaotic firing, Lyapunov exponents (LEs) areLE=(0.0347,−0.0017,−0.0194,−0.1069,−3.4759,−10.556)at 2500 seconds. The time evolution of Lyapunov exponents is plotted in Fig. 3, in the first 250 ms, the Lyapunov exponents fluctuated greatly, after 250 ms, the Lyapunov exponents saturated to an asymptotic value. And the Lyapunov exponents oft ∈(1250–1350) had no significant change from the value oft ∈(2400–2500). In Fig. 2(b), the parameterasets as 1.18, and other parameters remain unchanged. Without considering the coupled and self-feedback magnetic field, the membrane potentialxperforms a periodic spiking firing. At 1000 s, after a time-varying selffeedback magnetic field is added to the system,i.e.,Im1=(i−j·tanh(ϕ1))x1,Im2= (i−j·tanh(ϕ2))x2, the neuron’s firing pattern becomes a periodic spiking firing with a larger firing amplitude. At 2000 s,when the coupling magnetic field is added,i.e.,Im1=(i−j·tanh(ϕ1)+k·tanh(ϕ2))x1,Im2=(i−j·tanh(ϕ2)+k·tanh(ϕ1))x2, the neuronal firing pattern becomes periodic bursting firing. The results in Fig.2 confirm that the static neurons in the network can be activated by the magnetic field and produce a wealth of firing behaviors,such as spike firing,burst firing and chaotic firing. Besides,the introduction of the coupling magnetic field and the time-varying self-feedback magnetic field can transform the firing pattern of neurons,make the firing behaviors of the membrane potential more complicated and increase the firing amplitude.

Fig.2. Membrane potential time series with different parameters,where the self-feedback magnetic field and the coupling magnetic field are switched at t=1000 and t=2000 time units,(a)a=0.86,resting state during t ∈(0–1000)with no magnetic field,i.e., j=0,k=0;periodic bursting firing during t ∈(1000–2000)with j=3.8,k=0;chaotic firing during t ∈(2000–3000)with j=3.8,k=1. (b)a=1.18,periodic spiking firing in t ∈(0–1000)with j=0,k=0;periodic spiking firing with higher amplitude in t ∈(1000–2000)with j=3.8,k=0;periodic bursting firing with higher amplitude in t ∈(2000–3000)with j=3.8,k=1,where the inserted figures on the top are the enlarged versions corresponingly.

Fig.3. Time evolution of Lyapunov exponents with parameters a=0.86, j=3.8,k=1,Iext=3,where the inserted figures on the top are the enlarged versions corresponingly.

The common firing patterns of neurons are divided into four categories: quiescent state, periodic and chaotic bursting firings, periodic and chaotic spiking firings, and chaotic firing.[46,47]We further study the influence of different coupling strengths on the firing modes of the magnetic coupling neuron model. To this end, we set the coupling strengthkas the control parameter,and the external forcing currentIextremains unchanged during the simulation. Other parameters are the same as above. A bifurcation diagram is one of the essential ways to analyze the dynamics of the neuronal system.The determination of Lyapunov exponents is considered the most effective method to identify the system’s state.[48]The step size of the magnetic coupling strengthkis taken as 0.005,and the bifurcation diagram and the first three Lyapunov exponents diagram are shown in Fig. 4. As the magnetic coupling strength changes in the rangek ∈(−1.5, 2) , the neuron model experiences a significant change in the firing patterns. The negative symbol here indicates negative coupling.For a small coupling strength, the positive coupling strengthk ∈(0, 0.13) or negative coupling strengthk ∈(−0.12, 0) in Fig.4(b)two Lyapunov exponents converge to zero. Thus,the system appears as a pseudo-period bursting firing pattern with three spikes per burst. As the negative coupling strength is enhanced,the magnitude of the first and second spikes gradually decreases in the bursting firing. And when negative coupling strength isk=−1.39,the firing pattern is changed from bursting firing to two-period spiking firing. With the increase of the positive coupling strengthk ∈(0.13, 1.06), the cluster discharge amplitude and the number of spikes increase gradually. When the positive coupling strength is high in the rangek ∈(1.06, 2), in Fig. 4(b), the largest Lyapunov exponent is greater than zero;thus,the system shows chaos firing.

The timing diagram and phase diagram of the membrane potentialxare also presented in Fig.5 to observe the changes in the firing pattern. It is found that there are significant differences in the firing patterns of neurons with different magnetic coupling parameterk. The chaotics spiking withk=1.5, the bursting with five spikes per burst withk=1.35, the bursting with four spikes per burst withk=0.35,and the periodic spiking withk=−1.5 are shown in Figs. 5(a)–5(h), respectively. These results confirm that the coupling magnetic field between neurons can induce the generation of complex firing patterns and their mutual transition. For example,with the increase of the coupling magnetic field,the number of peaks in the bursting firing behavior of neuronal also increases, and it will experience a transition process from period 3 to period 7.

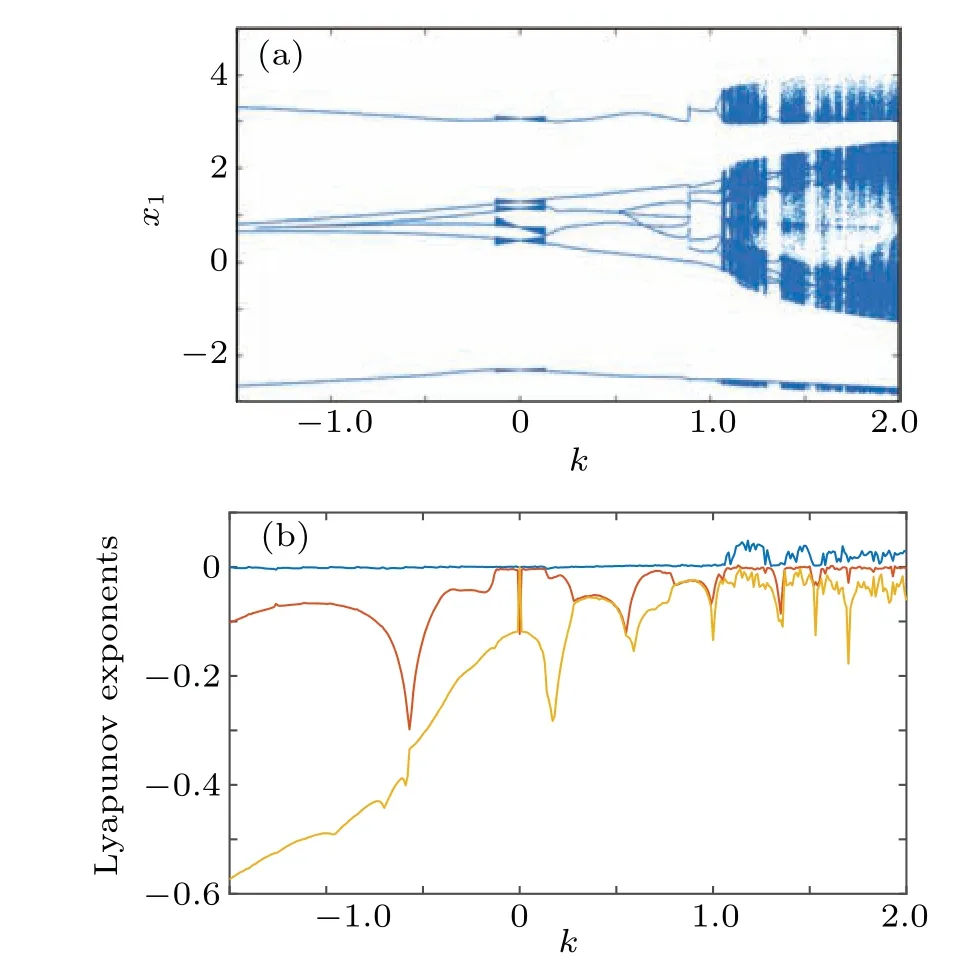
Fig.4.Evolution diagram reflecting electrical behaviors of the proposed neural model with respect to magnetic coupling strength k, with Iext =3. (a)Bifurcation diagram of membrane potential x1of k; (b)first three-Lyapunov exponents diagram of k.

Fig.5. Time series of membrane potential x1 and phase diagram of x1–ϕ1 in a neuron under different magnetic coupling strengths k with Iext=3;(a)and(b)chaotic bursting firing for k=1.5;(c)and(d)periodic bursting firing,five spikes per burst,for k=1.35;(e)and(f)periodic bursting firing,four spikes per burst,for k=0.35;(g)and(h)periodic spiking firing for k=−1.5.

3.2. Effect of time delay on neuron firing

Fig.6. Interspike interval(ISIs)bifurcation diagram with respect to external forcing current Iext,for time delay parameters;(a)τ =0,63%of the area being aperiodic;(b)τ =0.1,39%of the area being aperiodic;(c)τ =0.2,11.6%of the area being aperiodic;(d)τ =0.3,5.6%of the area being aperiodic.

Due to the limitation of signal transmission speed and the lag of neurotransmitter release,the time delay is inevitable in neural networks. This section mainly studies the changes in neuron firing patterns caused by the time delay in the feedback process of the time-varying magnetic field of magnetic coupling Bi-HR neurons. Transcranial direct current stimulation(TDC) and transcranial magnetic stimulation (TMS),[49,50]which uses weak electrical currents or magnetic fields to stimulate target areas of the brain to cause changes in the excitability of the nerve cell,[51]are both classic treatments for psychiatric disorders. Firstly,we set the external stimulation currentIextas the control parameter, fixk=3 and select four typical time delay values,τ=0,0.1,0.2,0.3,respectively. The interspike interval(ISIs)response of the neurons firing patterns for external forcing currentIextare plotted in Figs.6(a)–6(d).

In Fig. 6(a),τ= 0, in the ranges of external forcing currentIext∈{[0.5, 1.35], [1.56, 1.83], [2, 2.36], [2.52,2.62], [2.69, 2.71], [2.79, 2.9], [3.15, 3.28]}the firing pattern presents a chaotic firing state, accounting for 63% of the entire research range, which means that the system has a poor responseability to external signals.[50]However, with the increase of time delayτ,the firing pattern of neurons tends to be normal. Whenτ=0.1, in the regions ofIext∈{[0.88, 1.21],[1.25, 1.42], [1.48, 1.54], [1.79, 2.04], [2.23, 2.53], [2.83,2.91]}the firing pattern presents a chaotic firing state,accounting for 39% of the entire research range (Fig. 6(b)). Whenτ= 0.2, in the regions ofIext∈{[1.07, 1.09], [1.14, 1.17],[1.29, 1.36]}the firing pattern presents a chaotic firing state,accounting for 11.6%of the entire research region(Fig.6(c)).Whenτ=0.3,only in the regions ofIext∈{[1.29,1.3],[1.35,1.5]}the firing pattern presents a chaotic firing state,accounting for 5.6%of the entire research region(Fig.6(d)). And it can be seen that with increasing of time delay the neuron firing rhythm increased.

Fig.7. Bifurcation diagram of the maximum of the membrane potential x with respect to magnetic coupling strength k for delay parameters:(a) τ =0, many regions being aperiodic; (b) τ =0.1, some regions being aperiodic; (c) τ =0.2, some regions being aperiodic; (d) τ =0.3,fewer regions being aperiodic.

Next, we fix the external forcing currentIext=3, set the coupling parameterkas the control parameter,and select four typical values withτ=0, 0.1, 0.2, 0.3, respectively. A similar phenomenon is also found in the parameterkbifurcation graph,as shown in Figs.7(a)–7(d). With the increase of time delay, the abnormal discharge in the study area gradually decreases, and more bifurcation behavior occurs, which means that the responseability of neurons for the coupled magnetic field increases. These results confirm that time delay can induce the generation and transition of complex firing patterns.The smaller time delay, the weaker ability to respond to the external stimulus currentIextand it is easily appeared chaotic firing state. In a proper range,increasing the time delay value can make the nervous system have a better response-ability to the external forcing current and magnetic field, and make the neurons in the normal firing pattern.

4. Conclusion

The encoding and transmission of information in the nervous system are closely related to the different firing patterns of neurons.In this paper,we proposed a novel memristive dual neuron model based on magnetic field coupling. The memristor used in this model connects two neurons. The mathematical model of the memristor contains double hypervisor functions,respectively,representing a self-feedback magnetic field and a coupling magnetic field generated by adjacent neurons. In the numerical values and experiments,the interaction between the two adjacent neuronal cells of the magnetic field and the effect of the coupling magnetic field on the discharge mode were studied. It was found that coupled magnetic fields can activate resting neurons in the neural network. The firing pattern of neurons can be converted by changing the intensity of the coupled magnetic field in an appropriate range. The firing pattern of neurons can be changed from the spike to the cluster,and the number of spikes in the cluster can be changed regularly.This paper also studied changes in neuron firing patterns caused by time delay during magnetic coupling.By comparing the ISI bifurcation diagrams with external forced current as a variable under different time delays, it was revealed that increasing the time delay within a certain range can make neuronal cells in a state of periodic discharge under a wider range of external stimulus current. The same conclusion was obtained by adjusting the variable to coupling strength and analyzing the bifurcation diagrams.

This result will benefit the treatment and research of neurological diseases and provides new ideas for the treatment of arrhythmia, epilepsy, Parkinson’s and other neurological diseases. It is also of great significance to the coding and transmission of information in artificial neural networks. Besides,explaining the effect of magnetic field and time delay on the firing pattern of neurons from the perspective of energy will be the subject of our following research.