Thermal and mechanical properties and micro-mechanism of SiO2/epoxy nanodielectrics∗

Tian-Yu Wang(王天宇), Gui-Xin Zhang(张贵新), and Da-Yu Li(李大雨)

Department of Electrical Engineering,Tsinghua University,Beijing 100084,China

Keywords: nanodielectric,surface grafting treatment,molecular dynamics simulation,interface properties

1. Introduction

Epoxy resin (EP) is widely used in the field of insulation due to its excellent insulating properties, chemical stability, good mechanical properties, and low cost. However,with the increasing demand for electricity and the trend towards the miniaturization and integration of electrical equipment,ever-greater requirements for the various aspects of EP performance are being raised. Doping the insulating material with nanoparticles can effectively improve the insulating properties,thermal properties,and mechanical properties.[1–5]However,there are a large number of hydroxyl groups and unsaturated bonds on the surface of common nanoparticles(such as SiO2), and so the nanoparticles are in a highly chemically active and unstable state. Thus, they can easily agglomerate with other nanoparticles during the preparation of nanodielectrics, resulting in poor affinity with the polymer matrix(such as EP).[6]Some researchers have grafted a silane coupling agent to the nanoparticle surface to reduce the number of surface hydroxyl groups, and found that inhibiting the accumulation of surface charge and increasing the volume resistivity is more effective than pure SiO2nanoparticle doping.[6,7]Therefore,applying this surface grafting treatment to nanoparticles to reduce the surface hydroxyl content and then doping EP is a promising means of improving performance. However, to date, there have been few studies of the thermal and mechanical properties of doped surface-grafted nanoparticles in polymers. These properties of nanodielectrics are also very important for practical applications. Additionally, more importantly, owing to the limitations of the current experimental conditions,the change in the micro-mechanism of nanodielectrics after the grafting treatment remains unclear. Therefore,in this article,we will try to solve the above problems.

With the rapid development of computer science,molecular dynamics (MD) simulation technology is being widely used for new material design and polymer synthesis.[8–10]At the same time, the MD simulations can analyze materials on an atomic scale, allowing the macro performance and micro structure of the material to be combined.In recent years,some scholars have studied the properties of EPs and their composite materials through MD simulations,[11–15]and the results obtained by MD simulation are basically the same as the actual experimental results,[11–21]indicating that the results of MD simulation have high reliability. At present, MD simulation has gradually become one of the important scientific research methods.[22]For example, Wanget al.[23]and Shenet al.[24]conducted the MD simulations of epoxy resin doped with C60and graphene, and they found that the relative permittivity of the system was reduced. Shenet al.performed MD simulations on graphene/epoxy resin composites and studied the influence of the number of layers and the size of the graphene on the thermal conductivity of the polymer.[11]Wanget al.analyzed the covalent bonds of the SiO2/epoxy nanocomposite interface through the molecular simulations and believed that the covalent bonds formed at the interface are the reason for the increase in the glass transition temperature of the polymer and the reduction in the mobility of the molecular segments.[12]Fasanelia and Sundararaghavan simulated the thermal conductivity of single-walled carbon nanotube/epoxy resin composites and studied the changes in thermal conductivity of composites doped with different types of single-walled carbon nanotube.[13]Gouet al.studied the interactions at the interface between single-walled carbon nanotubes and epoxy resin.[14]Junget al.simulated the doping of nitrogen-modified carbon nanotubes into epoxy resin and found that the mechanical properties of the polymers were improved.[15]

In our previous work, we found experimentally that the epoxy resin doped with SiO2nanoparticles grafted with hexamethyldisilazane (HMDS) on the surface can effectively inhibit the surface charge accumulation,increase the volume resistivity, and improve the insulation performance.[6]Thus, in this study,the MD simulations are used to investigate the doping of EP with traditional SiO2nanoparticles and with SiO2nanoparticles grafted with hexamethyldisilazane (HMDS) at surface grafting rates of 10%and 20%,respectively. The thermal and mechanical properties of these nanodielectrics and the microscopic mechanisms are studied in depth,and the conclusions obtained will provide guidance for the analysis and design of nanodielectrics in the future.

2. Methods

2.1. Model construction

2.1.1. Model structure and MD simulation

All MD simulations described in this work were conducted using Materials Studio 8.0. The EP molecule constructed in this study was bisphenol-A epoxy resin(DGEBA).The curing agent was an amine curing agent(593 curing agent,the adducts of diethylene triamine and butyl glycidyl ether).Diagrams of the molecular structures are shown in Fig. 1(a).The DGEBA molecule (degree of polymerization is 1) has epoxy groups on both ends,and the curing agent molecule has primary and secondary amine groups at one end. Spherical SiO2nanoparticles with a radius of 1 nm were constructed.Owing to a large number of unsaturated bonds on the surface of the constructed SiO2, hydroxyl groups were added to the surface to ensure consistency with the actual situation. The SiO2nanoparticles are shown in Fig. 1(b). The reason why SiO2nanoparticles with a smaller particle size are selected for the simulation in this paper is that if the size of the nanoparticles is normal (such as tens of nanometers), then the entire system will be very large. Limited by the computing power of the computer, each simulation experiment lasted a very long time. Since this work is devoted mainly to the study of physical properties and microstructure,if the entire system is scaled up or down,these properties will not be changed. These SiO2nanoparticles were then surface grafted with HMDS. The reaction equation for the surface grafting treatment is shown in Fig.2(a).The SiO2nanoparticles with surface grafting rates of 10%and 20%were constructed(that is,10%and 20%of the hydroxyl groups on the surface were replaced by HMDS).The surface-modified SiO2nanoparticles are shown in Fig.1(c).

A three-dimensional amorphous unit cell of each model was then constructed. Four models were constructed in this study, namely pure EP, EP doped with SiO2nanoparticles(SiO2/EP), SiO2nanoparticles with a surface grafting rate of 10% (10%-SiO2/EP), and SiO2nanoparticles with a surface grafting rate of 20% (20%-SiO2/EP). Table 1 shows the nanoparticle number and mass percentage of each molecule.

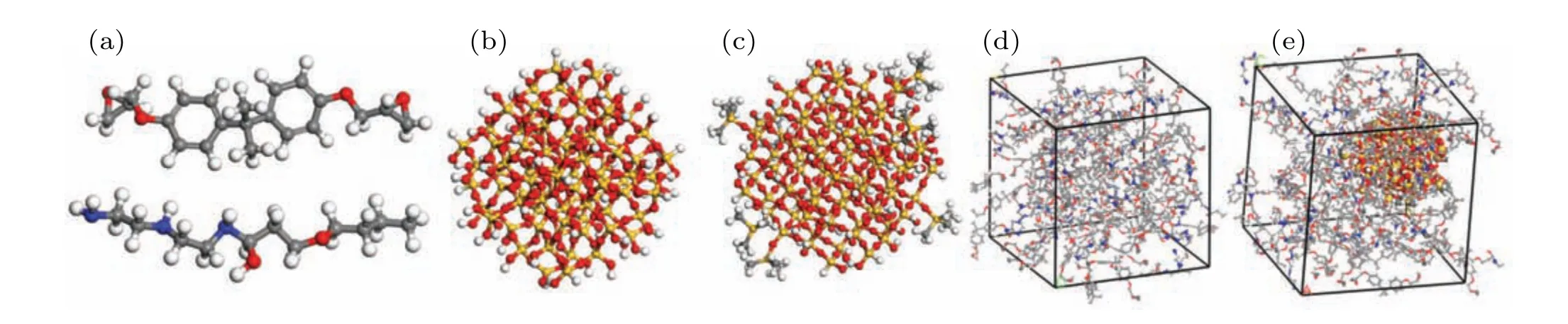
Fig. 1. Schematic diagram of molecular structure of model, showing (a) epoxy resin molecules (top) and curing agent molecules (bottom), (b) SiO2 nanoparticles with a radius of 1 nm, (c) SiO2 nanoparticles after surface grafting with HMDS (surface grafting rate 20%), (d) EP and (e) nanocomposite doped with SiO2 nanoparticles (this panel shows 20%-SiO2/EP), with white, gray, red, blue, and yellow balls representing H, C, O, N, and Si atoms,respectively.

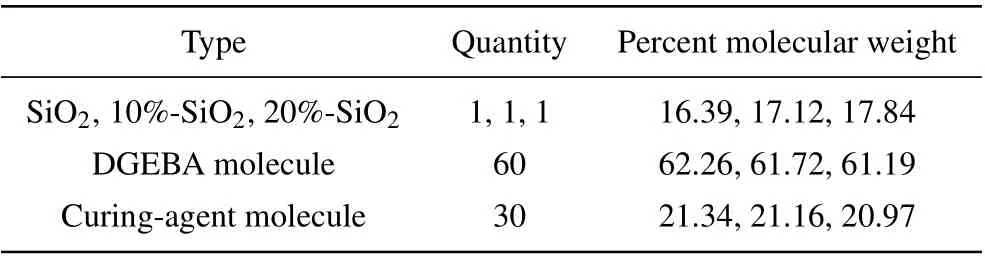
Table 1. Amorphous unit cell composition of composite system.

The initial density was set to be 0.6 g/cm3. With the subsequent structural optimization and other steps,the density of the system gradually approached to the actual density. All simulations described in this paper used the COMPASS force field. Atom-based method and the Eward method were used to calculate the van der Waals interaction and the electrostatic interaction,respectively,and the simulation quality was set to be medium.

2.1.2. Optmization of model structure

The structure of the three-dimensional amorphous unit cell was optimized to find the structure with the lowest energy. First, the steepest descent algorithm was used to optimize 3000 steps, and then the conjugate gradient algorithm was adopted to optimize 3000 steps. The model was then optimized for energy minimization. TheNVTensemble(an ensemble of particles with a constant number of particlesN, a constant volumeV, and a constant temperatureT) was used to balance 200 ps, and then theNPT(a constant pressureP)ensemble was used to balance 300 ps. The simulated temperature was 300 K, the MD simulation step was 1 fs, and the pressure was 1 atm (1 atm=1.01325×105Pa); the Andersen temperature control mode and the Berendsen pressure control mode were used.

2.1.3. Build epoxy resin cross-linking model

The crosslinking reaction process of DGEBA molecules and curing agent molecules are simulated in the subsubsection. The main reaction equation of DGEBA molecules with the amine curing agent is shown in Fig.2(b). The principle of simulating the crosslinking reaction is to first select the carbon atoms in the DGEBA molecule that can undergo the crosslinking reaction,and then search for the nitrogen atoms on the curing agent molecular around a certain cut-off range.A chemical bond forms between the carbon atom and the nitrogen atom.In the process of forming carbon–nitrogen bond,the breaking of carbon–oxygen bond and the forming of carbon–nitrogen bond correspond to the opening of the ring of epoxy molecule and the crosslinking between epoxy molecule and curing agent molecule,respectively. The criterion for whether a crosslinking reaction can occur is the cut-off distance. First,3.5 ˚A was set to be the cut-off distance, and all nitrogen atoms within 3.5 ˚A that can crosslink with carbon atoms were identified.As the degree of crosslinking increases,the formation of new chemical bonds becomes increasingly difficult. To accelerate the crosslinking reaction to the preset crosslinking degree,the cut-off distance was gradually increased to 8 ˚A in steps of 0.5 ˚A. Ideally, the crosslinking degree within the cut-off distance is 100%,but this is difficult to achieve in practice,so the crosslinking degree was set to be 90% and the reaction temperature was set to be 400 K. The process of simulating the crosslinking reaction was completed in the Perl language.

To make the model structure stable and closer to the real material, the crosslinked model was relaxed and quenched to eliminate the local internal stress of the model and make the density of the system close to the true value. The simulation for the case of running 100 ps at 500 K was conducted with theNVTensemble,and then theNPTensemble(an ensemble of particles with a constant number of particlesN, a constant pressureP, and a constant temperatureT) was used to simulate the case of running 500 ps at 500 K until the density and energy fluctuated are both in a very small range. TheNVTandNPTensembles were then used to cool the system from 500 K to 300 K at a cooling rate of 25 K per 400 ps(that is,every time the temperature drops by 25 K,theNVTensemble is used to simulate the case of running 100 ps,and then theNPTensemble is adopted to simulate the case of running 300 ps).Finally,theNPTensemble was used to run 500 ps at 300 K to obtain the final model.

Fig.2. (a)Reaction equation for surface grafting treatment of SiO2 nanoparticles with HMDS. (b) Main reaction equation of DGEBA molecule and amine curing agent.

2.2. Simulation principle of thermal performance

In this study,the changes in the thermal properties of materials in terms of the glass transition temperature (Tg), coefficient of thermal expansion(CTE),and thermal conductivity,are mainly considered. The density and volume of EP change with temperature. When the temperature is lower than theTgof EP, the EP is in a glassy state, and when the temperature is higher than theTgof EP, the EP is in a rubbery state. The value ofTgcan be obtained from the curve of specific volume(reciprocal of density)versustemperature. The intersection of the fitting line of temperature with the fitting line of specific volume refers to theTgof EP when the temperature is higher and lower thanTg.[25–27]

The CTE is used to analyze the thermal expansion and contraction of a material as the temperature changes. The formula for calculating CTE is[26,27]

whereV0is the initial volume of the system andVis the volume of the system when the temperature isT. The CTE is related to the slope of the fitted line of specific volume versus temperature when the temperature is higher or lower thanTg. When calculating CTE,the value ofV0when the material temperature is lower or higher thanTgis taken as the volume when the temperature is 300 K or 425 K,respectively.

The nonequilibrium molecular dynamics (NEMD)method was used to calculate the thermal conductivity of the material. The NEMD method constructed a stable temperature gradient under a fixed heat flux,and then the thermal conductivity of the material was obtained by using Fourier’s law.[28–30]In this study,the unit cell was divided into 20 parts in one direction,and the temperature of the material was taken as the average temperature of the model. The two edge layers were high-temperature layers and the middle two layers were low-temperature layers. The exchange of energy was achieved by exchanging the hottest particles in the cold layer with the coldest particles in the hot layer.

2.3. Principles of mechanical performance simulation

Mechanical properties are important indicators in the production and use of EP.This study simulated the changes in the bulk modulus, shear modulus, and Young’s modulus of different materials at different temperatures. The static constant strain method was used to calculate the mechanical properties of the system, and a small strain was applied to the equilibrium EP system. Through the response of the system to strain,a simplified stiffness matrixCi jcould be obtained for isotropic amorphous materials as follows:[31,32]

Fig. 3. Thermal performance simulation results, showing (a) change in specific volume with temperature, with vertical line denoting glass transition temperature,(b)thermal expansion coefficients of different materials in glassy state and rubbery state,and(c)thermal conductivities of different materials at 300 K.

By analyzing the changes in mean square displacement(MSD)with simulation time at different temperatures, the molecular chain-segment motion of the system could be determined.The greater the slope of the curve,the stronger the mobility of the molecular segment of the material is,which is a key factor affecting the mechanical properties of EP. The MSD is defined as[33,34]

whereβis the MSD of the system,Nis the total number of atoms in the system, andRj(t) andRj(0) are the displacement vector of any atomjin the system at timetand at the initial time,respectively. The angle brackets denote averaging over all chosen time origins.

The movement of molecular chains under the thermal field depends on the size of the free space. The polymer free volume ratio is given by

whereV0is the volume occupied by the molecules that constitute the substance andVfis the volume that accommodates the free movement of molecular segments in the system.

3. Results and discussion

3.1. Thermal properties

The simulation results for the thermal performance of different models are shown in Fig. 3. Figure 3(a) shows theTgvalues of the different models. Although doping with different types of SiO2nanoparticles gives a slight increase inTg, it is not much different from the undoped case. TheTgvalues of all models lie in a range of 402 K–410 K.

Figure 3(b)shows the CTE values of different models in the glassy state and the rubbery state. The doping of SiO2nanoparticles reduces the CTE of the system. If SiO2is surface grafted,this suppression effect is more significant,and a higher grafting rate produces a lower CTE value. When the surface grafting ratio is 20%,the CET value in the glassy state and rubbery state are only 83.2% and 54.9% of those for undoped EP,respectively. This shows that the thermal expansion and contraction of EP are both suppressed.This may be related to the small CTE of SiO2nanoparticles and the strong interaction between SiO2and EP molecules. The effect of a higher grafting rate producing a lower CTE value may be due to the increased affinity of SiO2molecules and EP molecules after surface grafting, which makes the interaction between SiO2and EP molecules more intense. The specific analysis is described in more detail in the EP molecular density distribution map around the SiO2nanoparticles in next subsection.

Figure 3(c) shows the changes in thermal conductivity of different models at room temperature. After doping SiO2nanoparticles,the thermal conductivity is slightly higher than that of the undoped system. According to the Maxwell–Eucken model, the thermal conductivity of a composite material is given by the following equation:[23]

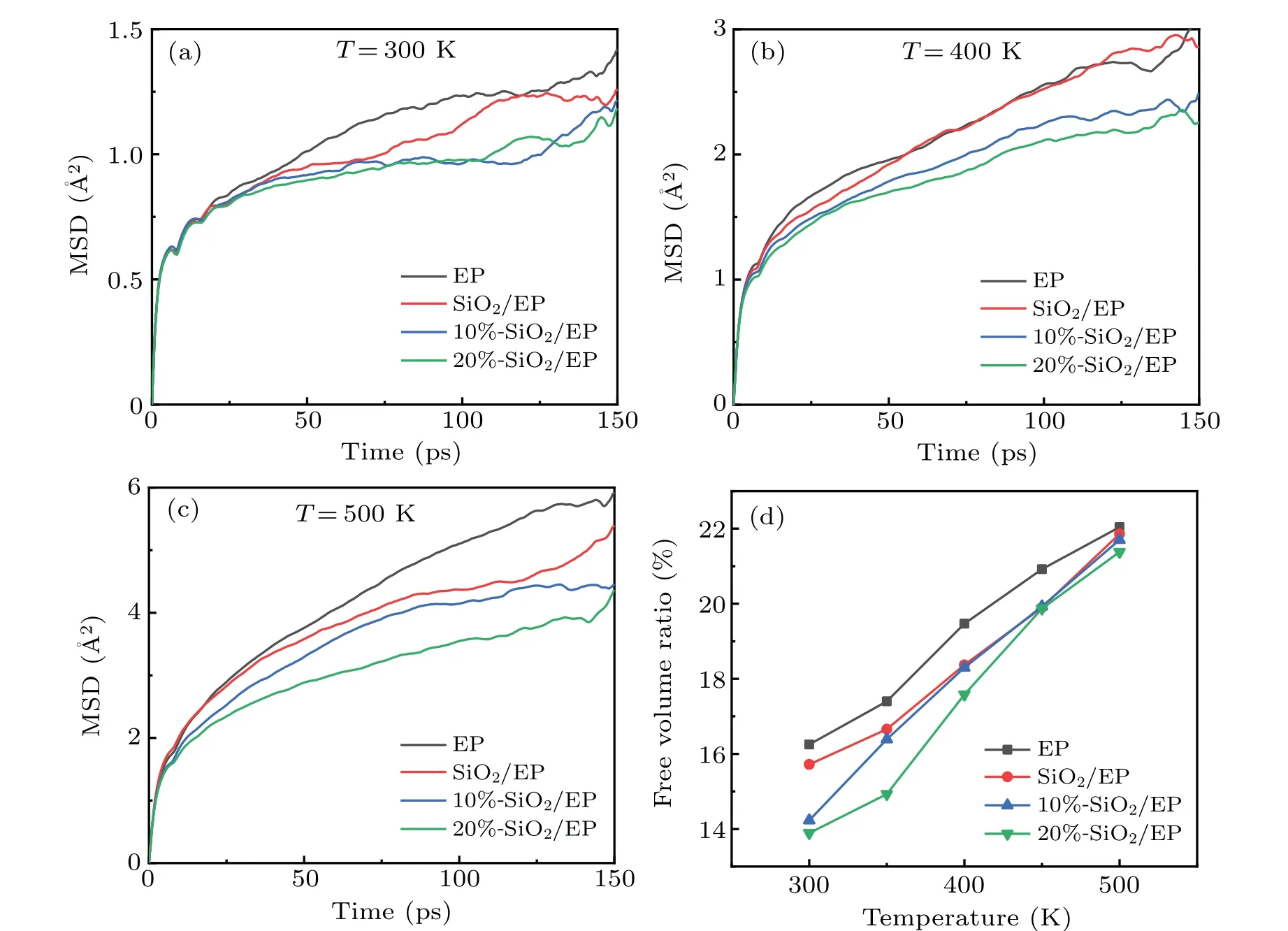
Fig.4. Curves of MSD versus time at(a)300 K,(b),400 K,and(c)500 K;(d)curves of free volume ratio versus temperature.

whereλ,λp, andλfare the thermal conductivity of the composite, polymer, and filler, respectively, andVfis the volume fraction of the filler. The thermal conductivity of EP is generally 0.2 W/(m·K),and that of SiO2is 1.4 W/(m·K).According to the above formula, the thermal conductivity of SiO2/EP is 0.235 W/(m·K).The thermal conductivity of EP is close to the simulation result,but the thermal conductivity of doped SiO2is slightly lower than the simulation result. This is mainly because the model ignores the influence of the formation of thermally conductive chains, so the thermal conductivity of the compound calculated by the model is slightly lower than that of the actual material.[25]After the surface grafting treatment of SiO2nanoparticles,the thermal conductivity of the system further increases,but not significantly. The reason for this can be analyzed by using the Agari model[35,36]

whereC1is a free factor for forming a thermally conductive chain andC2is a coefficient for the degree of difficulty of the filler forming a thermally conductive chain. This shows that after the surface grafting treatment of SiO2nanoparticles,the thermally conductive chains can form more easily,thereby improving the thermal conductivity of the system.

3.2. Mechanical properties

The MSD values of different models at different temperatures are shown in Fig.4.

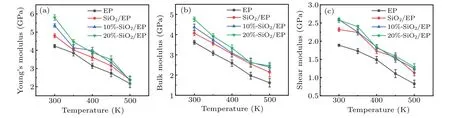
Fig.5. Simulation results of mechanical properties: temperature-dependent(a)Young’s modulus,(b)bulk modulus,and(c)shear modulus.

Fig.6. Behaviors of EP molecules in the interface area,showing(a)normalized EP molecular density in the interface area,and(b)temperature-dependent thickness of the van der Waals excluded region.

At different temperatures, the MSD value generally conforms to the following order: EP>SiO2/EP>10%-SiO2/EP>20%-SiO2/EP. This shows that the doping of SiO2nanoparticles effectively inhibits the movement of molecular chains in the system, especially the surface-grafted SiO2nanoparticles. Figure 4(d) shows the free volume ratios at different temperatures. From this figure, it is apparent that the free volume ratio exhibits similar properties. This is because the degree of molecular chain motion mainly depends on the proportion of free volume. At room temperature, the free volume ratio after doping with 20%surface-grafted SiO2nanoparticles is only 85.48%of that of EP.As the temperature increases,the MSD value and the free volume ratio gradually increase,indicating that a rising temperature enhances the degree of molecular chain movement.

Figure 5 shows the simulation results for the Young’s modulus,bulk modulus,and shear modulus.After doping with SiO2nanoparticles,especially surface-grafted SiO2nanoparticles,these values are improved,indicating that the mechanical properties have been improved. The reason for this is that in addition to the inhibition of the molecular segment movement mentioned above, there is stronger interaction between SiO2and EP molecules.

Figure 6(a) shows the density distribution of EP molecules around SiO2nanoparticles. After doping with SiO2nanoparticles, an interface region forms around the surface.In this interface area,the molecular density of EP is very low when it is less than 2.5 ˚A from the surface of the SiO2nanoparticles. This area is also called the van der Waals excluded region. The thickness of this area is defined as follows:[37]

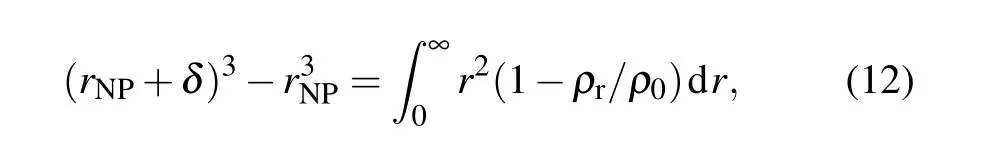
whereδis the region thickness,rNPis the radius of the nanoparticle,ρris the radial density from the surface of the nanoparticle to a given distancer,andρ0is the polymer bulk density of the system. At 300 K, after doping with SiO2nanoparticles, the thickness of the van der Waals excluded region is 2.5 ˚A, whereas after doping with 10% and 20%surface-grafted SiO2nanoparticles,the thickness values of the van der Waals repelling zone become 2.4 ˚A and 2.1 ˚A, respectively. This shows that chemical modification of the SiO2nanoparticles weakens the molecular repulsion force between SiO2nanoparticles and EP, which is consistent with the understanding that the compatibility between SiO2nanoparticles and polymers can be improved after grafting treatment. Figure 6(b)shows the variations ofδwith temperature at different temperatures. It can be seen that at any temperature,δfor the grafted SiO2nanoparticles is lower than that in the nongrafted case, and a higher grafting rate produces a lower value ofδ, which means that there is a higher density of EP molecules in the interface region. A higher molecular density corresponds to the better elastic properties, that is, better mechanical properties. This is also why the mechanical properties of the materials runs in the order 20%-SiO2/EP>10%-SiO2/EP>SiO2/EP.This is true at different temperatures,indicating that this material modification method has good thermal stability.

4. Conclusions

This study presents the results of MD simulations in which the SiO2nanoparticles and SiO2nanoparticles grafted with HMDS at 10%and 20%surface grafting rates are doped into epoxy resin. The thermal and mechanical properties of these nanodielectrics and the microscopic mechanisms were studied in depth. The main conclusions are as follows.

(i)After doping with SiO2nanoparticles,the glass transition temperature does not change significantly. However, the thermal expansion and contraction of the system and the thermal conductivity are improved,especially by the surface grafting treatment of SiO2nanoparticles. The main reason may be that after the surface grafting treatment,the thermal chains can form more easily.

(ii) After doping with SiO2nanoparticles, the mechanical properties of the system are significantly improved. Of the systems considered in this study,the improvement in mechanical properties can be ordered as follows:20%-SiO2/EP>10%-SiO2/EP>SiO2/EP>EP.We think,this is mainly related to two factors. First, the doping of SiO2nanoparticles inhibits the degree of movement of the molecular chains in the system,so SiO2/EP>EP.Second, after the surface grafting treatment,the molecular repulsion between SiO2and EP is weakened,and the van der Waals excluded region becomes thinner, that is,the compatibility between SiO2nanoparticles and polymer is improved by the grafting treatment. Thus, the mechanical properties are further improved,leading to the ordering 20%-SiO2/EP>10%-SiO2/EP>SiO2/EP.

Based on the analysis in this article, we believe that the surface grafting treatment of SiO2nanoparticles with HMDS and then doping into epoxy resin can effectively improve the thermal and mechanical properties of the system, and has strong potential practical applications in future.