基于反应热严格计算的加氢裂化反应器建模

李圣淋，李国庆，王 艳，蔡楚轩

(华南理工大学 化学与化工学院，广东 广州 510640)

加氢裂化(Hydrocracking)是石油馏分烃分子在较高反应温度和压力下，在催化剂表面进行裂解和加氢反应，生成较小烃分子的转化过程[1]。由于该技术具有原料适应性强、产品清洁等优点，正成为油品质量升级和原油高效加工的关键技术之一[2]。加氢裂化原则流程如图1所示。

图1 石油馏分加氢裂化装置原则流程示意图Fig.1 Diagram of petroleum fraction hydrocracking unit

由图1可知：升压、混氢后的原料被加热炉加热到一定温度后进反应器(根据需要可设置1个或者多个反应器，每个反应器设置多个床层)，反应产物从底部排出，经与原料换热降温后送油-气分离单元，分离出循环氢，再送分馏系统，经蒸馏和吸收稳定等工艺，得到干气、液化气(Liquefied petroleum gas,LPG)、轻石脑油、重石脑油、航煤、柴油和尾油。显然，全流程中反应器最为关键，必须正确建模其内部反应机理[3]。

石油馏分高度复杂，长期以来多沿用集总理论(Lump theory)进行机理研究。所谓集总就是将无法描述其分子组成的复杂反应体系，按约定规则，将其反应动力学特征相近的组分划分成一个个性质可描述的虚拟组分即集总(Lump)，使原本不可描述的反应体系近似抽象成可描述体系，从而使定量研究成为可能[4]。

石油馏分加氢裂化集总建模大致经历了宽集总和窄集总2个阶段。宽集总研究始于1939年，Qader和Hill[5]将反应体系分成原料(≥350 ℃馏分)和产物(<350 ℃馏分)2个集总。此后，Yui等[6]建立了重瓦斯油(Heavy gas oil,HGO)转化为轻瓦斯油(Light gas oil,LGO)和石脑油(Naphtha)的三集总模型，气体被归入石脑油集总。Sadighi等[7]则将原料蜡油和尾油划为1个集总，裂化生成的馏分油、石脑油和气体各划为1个集总，并首次考虑了耗氢，这便是有名的四集总模型。在其后的研究中[8]，进一步将馏分油和石脑油集总细分为柴油、煤油、重石脑油和轻石脑油，建立了六集总模型，计算表明六集总模型的产品误差在可接受范围。可见，宽集总模型仅依据原料和产品方案划分集总，故不适于产品改变的工况，局限性较大。

窄集总按反应体系某连续性质的分布划分反应体系。在石油馏分加氢裂化研究领域，最负盛名的窄集总模型是Chevron模型[9]。其认为反应体系中的原料和产品都是具有连续蒸馏曲线的化合物，化合物的加氢裂化性能由实沸点决定。于是从初馏点开始，每隔50 ℉(27.7 ℃)切割一次，将这些化合物分成若干个窄馏分，即集总，并假设窄馏分的中平均沸点就是集总的实沸点。由于克服了固定沸程集总模型无法反映产品方案变化的缺点，以及引入了对C4组分特别处理的分布函数(Pi,j)，Chevron模型大获成功。

Chevron模型假设集总间只发生一级、等温、非可逆反应，同时引入B(产物分布常数)、D(第一集总收率系数项常数)、ω(第一集总收率指数项常数)参数表征产品分布，故只要基于模型计算值与实验值误差最小原则倒拟合出反应体系的模型参数，石油馏分加氢裂化的机理建模就完成了。模型参数有6个，分别是E(反应活化能)、K0(反应速率常数指前因子)、A(指前因子温度校正系数)以及B、D和ω。

接下来Chevron模型基本主导了石油馏分加氢裂化研究。但鉴于其等温反应假设与实际反应相悖，Mohanty等[10]引入了热量方程组概念，并提出了近似计算加氢裂化反应热的方法。Pacheco等[11]则第一次将反应氢耗纳入物料平衡，并假设集总反应方程化学计量系数等于相应的产物分布函数Pi,j，但被Li等[3]否定，他们基于反应过程碳平衡，推出了严格的化学计量系数计算公式，从而使模型的物料平衡以及化学氢耗计算更加准确。Zhou等[12]建立了兼顾加氢处理和加氢裂化的反应器模型，用遗传算法(Genetic algorithm,GA)[13]拟合模型参数，实验表明其精度良好。而Bhutani等[14]在拟合Chevron模型参数时，除考虑产品收率和温度分布误差外，还兼顾了集总收率误差，只是继续沿用经验权重因子，效果不甚明显。Li等[15]基于Chevron假设和反应过程物料平衡，推导出了利用反应集总进、出反应体系的浓度直接计算指前因子温度校正系数A的方法，减少了一个模型参数，不但大大减少了计算量，还提高了模型精度。但几乎无一例外，以上研究对反应热(ΔHa)的处理都沿用式(1)的假设[3,10]。

ΔHa=2.1×104kJ/kg H2

(1)

式(1)表明离散集总石油馏分加氢裂化过程每消耗1 kg氢气，将释放2.1×104kJ反应热。这种恒反应热假设无疑与实际反应不符。反应热应与原料性质、产品分布等有关。具体到加氢裂化反应器，沿床层高度不同，集总分布和温度不同，单位质量反应热必然不同，所以要精确处理。

综上所述，笔者将从下述几个方面致力于这一研究。

(1)基于化学反应过程中氢、碳元素质量平衡[3]，计算反应物集总、反应产物集总以及耗氢的化学反应计算系数，以准确描述石油馏分离散集总加氢裂化反应体系，为严格计算反应热奠定物料平衡基础；并采用流程模拟技术计算石油馏分集总物性，进而计算反应物集总、反应产物集总的标准燃烧热。

(2)依据热力学状态函数法，计算反应体系在不同温度和压力条件下的反应热，以及反应热对床层温度分布和产品分布的影响，进而改进Chevron模型。

(3)基于温度分布误差和产品分布误差同时最小原则，以多目标遗传算法(NSGA-Ⅱ)拟合模型参数，提高参数精度。

(4)将改进模型和NSGA-Ⅱ参数拟合方法应用于某实际蜡油加氢裂化反应器，检验研究效果。

1 反应器模型

基于严格反应热计算，建立起新的石油馏分离散集总Chevron加氢裂化工业反应器机理模型。

1.1 反应体系

为研究石油馏分加氢裂化过程的物料平衡和能量平衡，对反应体系做如下处理和假设：

(1)按实沸点(True boiling point,TBP)由重到轻，以25 ℃间隔，将反应体系切割成N个集总，如图2所示。由图2可知：重集总可转化为轻集总，但不能转化为次重集总；T(TBP)<127 ℃的轻集总不裂解，集总性质用平均TBP温度下的油品性质表征。

(2)集总反应均为一级不可逆反应[10]，忽略聚合反应，忽略传质阻力。

(3)反应器为平推流反应器，无径向返混。

(4)反应器呈稳流、绝热状态运行。

(5)新氢和循环氢均视为纯氢。

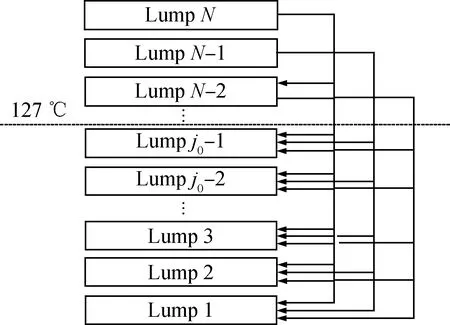
N—The serial number of the heaviest lump；1—The serial number of the lightest lump；j0—The serial number of the lightest lump that may crack图2 反应系统集总理论描述Fig.2 Lump description of the reaction system

式(2)～(5)是集总裂化反应的化学反应方程式组。其中，式(2)可描述图2的系统集总理论反应体系。

(2)

(3)

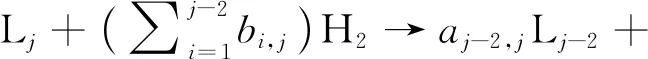
(4)

…

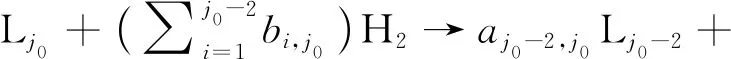
(5)

式(2)～(5)中，L表示集总，bi,j是第j个集总裂化生成较轻的第i个集总消耗氢气的化学计量数，a是产品集总的化学计量数。N是最重集总编号，j0是可以裂化的最轻集总，j0-1是不可裂化的最重集总。i=1、2、…、N-2；j=j0、j0+1、…、N。

1.2 反应速率方程

基于一级反应假设，Chevron模型定义反应速率为：

(6)

(7)

式中:ri是第i个集总的反应速率，kg/(kg催化剂·s)；Pi,j是第j个集总裂解生成第i个集总的概率，%，又称分配系数；Mt是进入催化剂床层的液体物料总质量流率，kg/s；ci是第i集总的质量分数(高氢/油比反应，%，不考虑c(H2))；m是催化床程的催化剂装填量，kg；ki是第i集总一级反应速率常数，kg反应物/(kg催化剂·s)，按式(8)、(9)计算。

(8)

Yi=(1.8T(TBP)i+32)/1000

(9)

式(8)～式(9)中:R是理想气体常数，即R=8.314 kJ/(kmol·℃)，T和E分别是反应温度(℃)和活化能(kJ/kmol)，T(TBP)i是第i集总的平均实沸点(℃)，Yi是中间变量，K0是反应速率常数指前因子(kg反应物/(kg催化剂·s))，A是指前因子温度校正系数(无量纲)，与反应原料性质有关[11]。Chevron模型认为所有集总的E、A、K0均相同。显然，T(TBP)≤127 ℃的集总ki=0。

定义P′i,j=P1,j+P2,j+…+Pi,j，即第j个集总裂解成为≤i的全部集总的分配函数之和，见式(10)～(14)所示。

Pi,j=P′i,j-P′i-1,j

(10)

对第一集总(即丁烷及更轻组分)：

P′1,j=D·e-ω(1.8T(TBP)j-229.5)

(11)

对其余集总：

(12)

(13)

显然：

(14)

式中:yi,j是沸点归一化中间变量；B是产物分布常数；D是第一集总收率系数项常数；ω是第一集总收率指数项常数。Chevron模型认为所有集总B、D、ω值相同。

文献[3]依据石油馏分加氢裂化反应过程碳元素质量守恒原理，推导出了式(2)～(5)中化学反应计量系数ai,j和bi,j的计算公式(15)和(16)。

(15)

(16)

(17)

wH,i=-15.08+2.55312Ki-0.0022248(32+1.8T(TBP)i)

(18)

(19)

式中，Mw,i、Ki、di、wH,i和fi分别是第i集总的平均摩尔质量(kg/kmol)、特性因数、相对密度、氢元素质量分数(%)和碳/氢质量比。

可见，Chevron石油馏分加氢裂化离散集总动力学模型有E、K0、A、B、D、ω共6个待定模型参数。

1.3 反应热计算

利用石油馏分集总标准燃烧热计算加氢裂化反应热。

1.3.1 集总反应热

依状态函数[16]理论，Lj集总反应过程可分解为图3所示过程。

于是，第j集总加氢裂化反应热ΔHLj列与式(20)。

ΔHLj=ΔHj,1+ΔHj,3-ΔHj,2-ΔHj,4

(20)

其中：

(21)

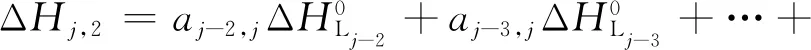
(22)

Bj—The jth lump；bi,j—The stoichiometric coefficient of hydrogen consumed for the heavier jth lump when it is cracking into the lighter ith lump；aj-2,j—The stoichiometric coefficient of the lighter ith lump when it is cracked from the heavier jth lump；ΔHj,1—The combustion enthalpy for both the lump Bjand the hydrogen consumed during the hydrocracking under T0 and p0 (kJ/kmol)；ΔHj,2—The combustion enthalpy for the lighter lumps cracked from the lump Bjunder T0 and p0 (kJ/kmol)；ΔHj,3—The enthalpy change of temperature changing from T1 to T0 for both the lump Bj and the hydrogen consumed during the hydrocracking (kJ/kmol)；ΔHj,4—The enthalpy change of temperature changing from T2 to T0 for both the lighter lumps cracked from the lump Bj (kJ/kmol)；ΔHj—The enthalpy change of hydrocracking for one mole of the jth lump (kJ/kmol)；p0,T0—The reference pressure (Pa)and the reference temperature (℃)；p1，T1—The pressure (Pa)and the temperature (℃)of the system before the hydrocraking reaction；p2，T2—The pressure (Pa)and the temperature (℃)of the system after the hydrocraking reaction图3 基于标准燃烧热计算反应热过程示意图Fig.3 Calculation demonstration of reaction heat by means of standard combustion enthalpy

加氢裂化反应发生前后的压力变化对各组分的比热容的影响很小，故忽略压力影响，则：

(23)

(24)

式中：Cp,Lj和Cp,H分别是集总Lj的定压比热(kJ/(kmol·℃))和氢气的定压比热(kJ/(kmol·℃))。其中，Cp,H可按式(25)计算[18]。

Cp,H=27.143+9.274×10-3T-1.377×10-5T2

(25)

说明只要知道集总Li(i=j-2,j-3,…,1)的标准燃烧热和比热就能计算集总Lj的反应热。

对石油馏分集总来说，标准质量燃烧热ΔH0(kJ/kg)和平均质量比热Cp(kJ/(kg·℃))可分别按式(26)[19]和式(27)[20]计算。

ΔH0=8505.4+846.1K+114.92(°API)+
0.12186(°API)2-9.951K·(°API)+91.23wH

(26)

Cp=(1.428+0.231K)((0.6811-0.308d)+
(0.000815-0.000306Gs)(32+1.8T(TBP)))

(27)

式中：K、°API、Mw、T(TBP)、d和wH分别是集总的特性因数、比重指数、摩尔质量(kg/kmol)、平均实沸点(℃)、相对密度和氢元素质量分数(%)。前4项可由Aspen Plus模拟得到。wH可由式(18)计算得到，均与温度无关。Gs与温度相关，按式(28)～(34)计算[21]。

(28)

ρ=ρ0/(1-p×10-6/D1)

(29)

D1=(z·X+D2)

(30)

z=188.1+0.03739p+0.00022735p2-1.9396×10-7p3

(31)

D2=22.744+4.395p-0.002954p2+
1.6283×10-6p3

(32)

X=(D3-564.0)/197.1

(33)

lgD3=-0.001098t+0.7133ρ0+2.7737

(34)

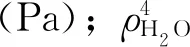
1.3.2 加氢裂化反应体系总反应热

加和各集总反应热ΔHLj，j=j0、j0+1、…、N，kJ/kmol，便可由式(35)得到体系总反应热Q，kJ/(kg·s)。

(35)

式中:ri是第i个集总的反应速率，kg/(kg催化剂·s)；m是催化床程的催化剂装填量，kg。

1.4 加氢裂化反应床层温度分布

因加氢裂化反应产物分布及反应热均与温度密切相关，故定量了解加氢裂化反应器各级反应床程的温度分布是必要的。

图4是第k级反应床程(k=1～6)示意。由于加氢裂化反应放热，体系温度由入口Tk,1(℃)变为出口Tk,2(℃)，产物则因急冷氢(质量流量GH,k+1(kg/s)、温度TH(℃))的注入，从Tk,2(℃)降温到Tk+1,1(℃)，并以此温度进入第k+1级床程。

图4 第k级反应床程温度分布Fig.4 Temperature distribution of kth fixed-reaction bed

忽略外壁散热，微元dz有如下热平衡：

Gk·cp,k·dtk=ρk·Qk·Sk·dZk

(36)

dZk=uk·dt

(37)

式中，Z和S分别是反应器高度(m)和横截面积(m2)，u和t分别是反应器中物料流速(m/s)和流通时间(s)，G、cp、ρ和Q分别是反应器中物流的质量流量(kg/s)、比热(kJ/(kg·℃))、密度(kg/m3)和单位质量反应热(kJ/(kg·s))，k为第k级反应器。

对应的积分式如式(38)～(39)所示。

(38)

(39)

式中：第k级反应器的横截面积Sk(m2)已知；因反应器内物流稳定流动，第k级反应器的流量Gk(kg/s)、流速uk(m/s)是常数，且已知。Gk采用式(40)计算，ρk采用式(41)计算，Qk采用式(35)计算，cp,k采用式(42)计算。

Gk=Gk-1+GH,k

(40)

(41)

(42)

第k级反应器出口因急冷氢注入，出口温度Tk,1变为：

(43)

至此，新的基于严格反应热计算和严格氢碳元素平衡的石油馏分离散集总Chevron加氢裂化反应器机理模型建立完毕。

2 计算模型参数

新的基于严格反应热计算和严格氢碳元素平衡的石油馏分离散集总Chevron加氢裂化反应器机理模型的6个模型参数是E、K0、A、B、C、ω，对其进行计算。对6个模型参数分别设定6个初值，代入上文所建立的反应模型计算式，计算出相应的反应器床层温度分布参数和产品分布参数，然后检验其与实测值(或现场值)是否一致，一致说明初值准确，否则重来。因此，从数学上讲模型参数就是误差最小方程的解。

误差定义有多种方式，最常见的如式(44)所示[3,14,22-23]。

(44)

式中：kn是床层数；Gkn是末级床层出口质量流量，kg/s；Tk,2,mea和Tk,2,mod(k=1，2，…，6)分别表示第k级床层出口的温度实测值(℃)和模型计算值(℃)；wi,mea和wi,mod(i=1，2，…，6)表示产品气体、轻石脑油、重石脑油、航煤、柴油和尾油的质量分数实测值(%)和计算值(%)；λi是权重因子(i=1，2，3)，大小由研究者确定，如取λ1，λ2=1000，λ3=0，则意味着模型轻产品分布预测，重温度预测，不考虑末级流量预测。显然，该方法是经验型的，是基于总误差最小开展的单目标优化计算。

另一种方法如式(45)和(46)所示，基于温度误差和产品分布误差同时最小计算模型参数[15]。

(45)

(46)

这是六变量双目标优化问题，鉴于其高度非线性，拟采用基于精英策略的非支配排序遗传算法(Non-dominated sorting genetic algorithm,NSGA-II)[24-27]求解。原因是：(1)NSGA-II采用Pareto最优解集，为多目标优化提供了可能；(2)其简洁明晰的非支配排序，使算法具有逼近Pareto最优解前沿的能力；(3)当同一个算法迭代层中的个体(该层包含的解)不能全部进入父代种群时，采用拥挤度(Crowing distance)机制筛选，保持了种群的多样性，扩大了搜索范围，其Pareto最优解具有良好分布；(4)非支配排序和拥挤度筛选的复杂度并不高，易于电算化。

图5是采用的模型参数计算框图。

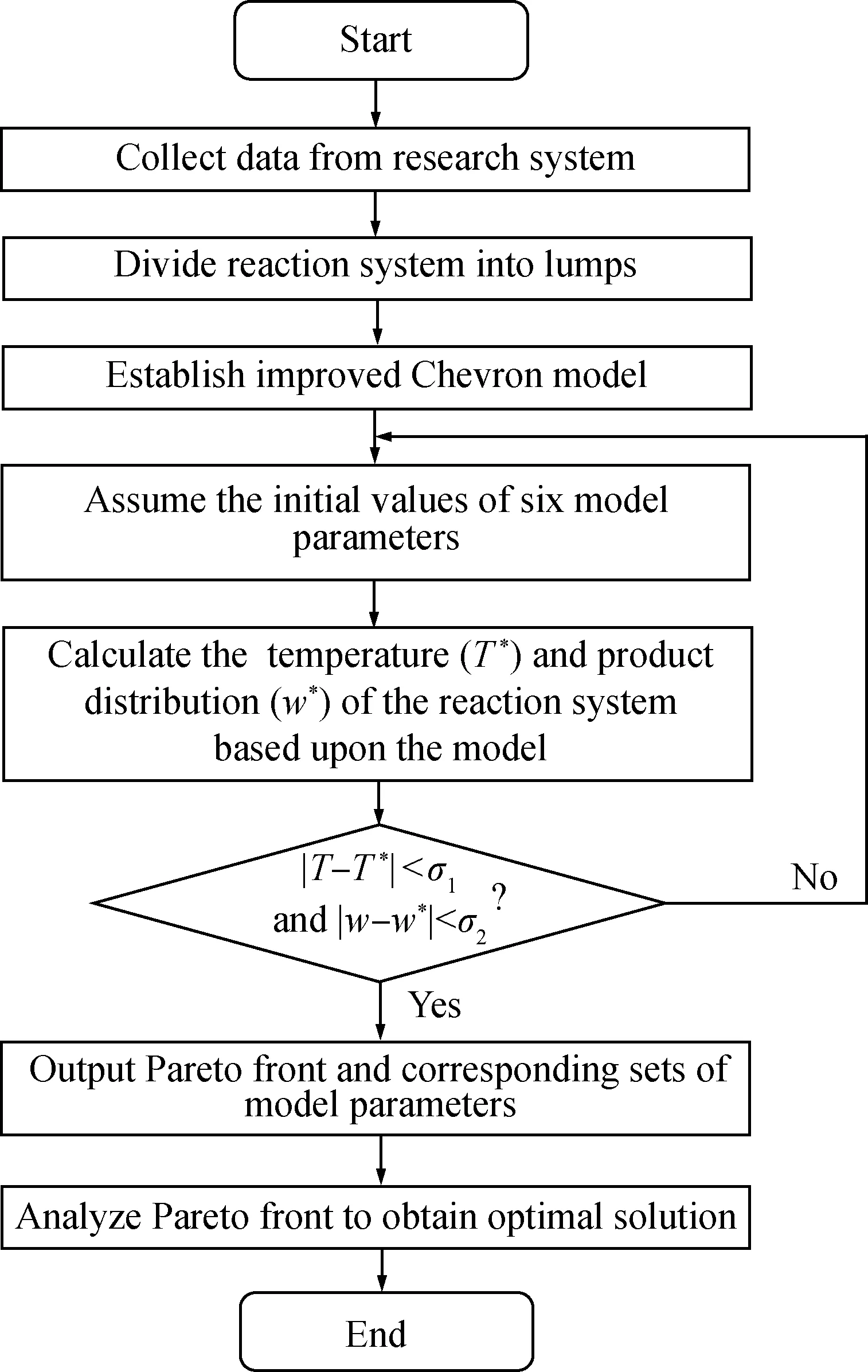
图5 利用NSGA-II计算模型参数Fig.5 Calculation block for 6 model parameters with NSGA-II

由图5可知：首先收集现场数据进行反应体系集总划分，然后建立起改进的Chevron模型，再设定6个模型参数初值，在MATLAB软件环境中利用NSGA-II算法计算加氢裂化反应体系的温度和产品分布。重复以上操作，直至计算值与实际值的误差符合期望，然后输出Pareto前沿解集，并进行解集分析，最终得到6个模型参数，将它们植入改进的Chevron模型，则加氢裂化反应器机理建模完成。

3 案例应用

以某炼油厂双系列、单反应器6床层2.0 Mt/a蜡油加氢裂化装置反应器为例，建立模型并检验模型对于反应器出口温度和产品分布的预测效果。

3.1 划分集总和建立反应体系

从现场DCS(Distributed control system)系统的PHD(Process history database)数据库采集了40个连续工作日的数据，包括反应器各床层出口温度、反应压力、反应器出口产品分布以及原料和产品性质等。每天从中选1组数据，经过圆整形成40组较为完整且有一定差异的数据，并选取其中1组数据，在Aspen Plus模拟帮助下，按等25 ℃温度间隔将反应体系划分成如表1所示的22个集总。

根据表1中数据建立反应体系，即确定式(2)～(5)中的反应产物集总系数ai.j和反应物集总化学氢耗系数bi.j。以第19集总裂化生成第21集总为例，经Aspen模拟得到No.19和No.21集总的特性因数(K)，平均摩尔质量(Mw)和平均实沸点(T(TBP))，再以式(7)～(9)由参数B、C、ω的初值计算得到分配函数P19,21(并非最终计算结果)，最后根据式(12)～(16)计算得到其mH、f、a19,21、b19,21值如表2所示。

表1 反应体系集总划分及集总性质Table 1 Lump partition for a reaction system and the properties of lumps

表2 加氢裂化反应体系参数Table 2 Parameters of hydrocracking reaction system

3.2 加氢裂化反应新模型计算应用

3.2.1 加氢裂化反应热计算

表3 集总反应热计算结果Table 3 Calculation results of lumps reaction heats

3.2.2 模型参数计算

基于加氢裂化反应器反应床程温度分布误差和末级床层产品分布误差双目标同时最小计算目标函数。基于文献[3]所给出的参考值范围，设定6个模型参数的初值如表4所示。

表4中的参数基于NSGA-II实施参数拟合，为此设定其相关参数如表5所示。

表4 模型参数初值Table 4 Initial values of 6 model parameters

如表5所示，设定运行算法的种群大小为200，停止标准分别为最大运行代数200，最大停滞代数100。基于NSGA-II计算得到模型参数帕雷多前沿解(Pareto front)解集如图6所示。

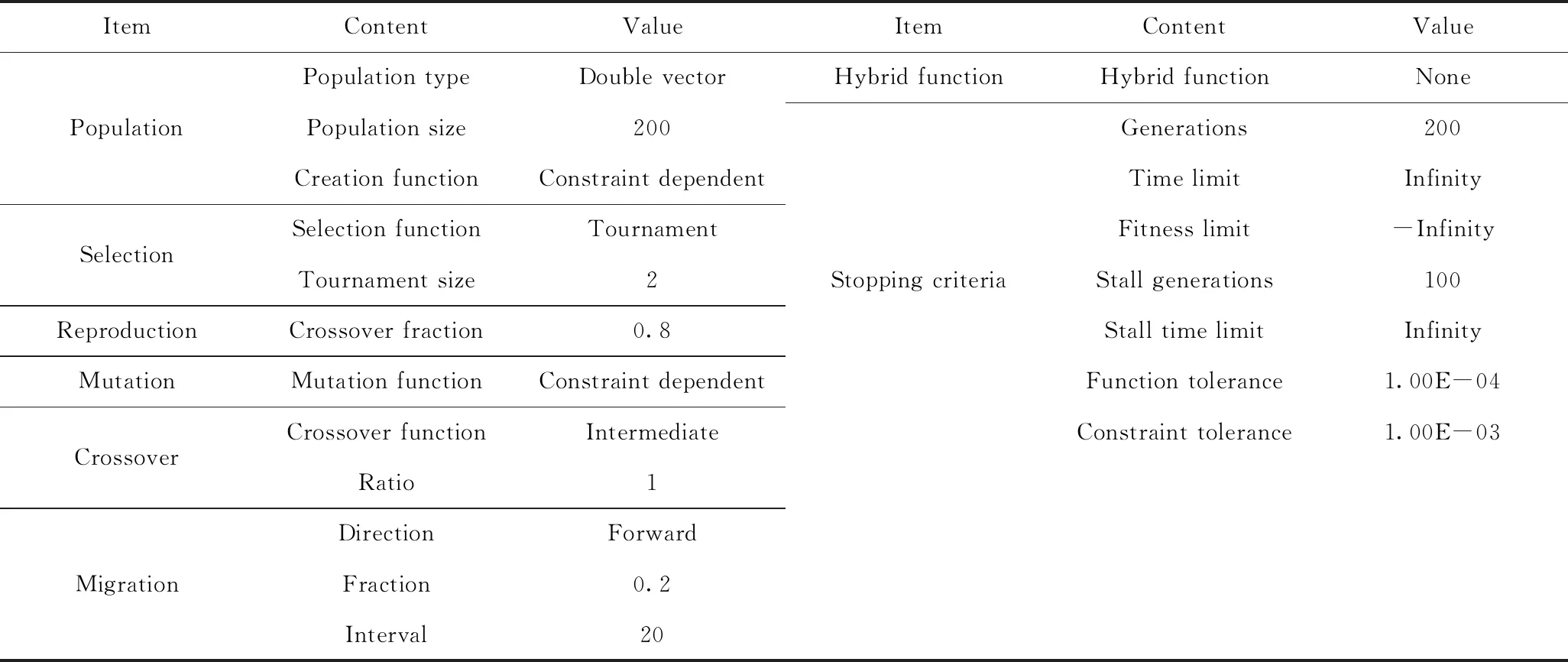
表5 研究采用的NSGA-II算法参数Table 5 Stipulation for algorithm parameters of NSGA-II in this study

Error1—Cumulative error of product distribution；Error2—Cumulative error of product output temperature图6 模型参数计算Pareto前沿解集Fig.6 Pareto set for calculated specified model parameters

由图6可知：其曲线上的每个点都是NSGA-II最优解，都对应着一组模型参数及误差。如何选择，不同研究者有不同决策[28]。笔者采用Deng等[29]的灰色相关分析法，好处是无需提供权重或其他输入(详细步骤见文献[30])。图6中红点和绿点都是GRA最优解，以红点作为终选，对应模型参数如表所示。

由表6中的6个参数便可以建立起该蜡油加氢裂化反应器之基于严格反应热计算的Chevron模型。

表6 从Pareto前沿解集中选择的模型参数Table 6 Model parameters used in revamped Chevron model

3.3 加氢裂化反应器新模型的计算精度

检验加氢裂化反应器新模型的反应器出口温度和产品分布的预测精度，即分析其相对误差(β)，可由式(47)和(48)计算得到。

β=(Tk,2,mod-Tk,2,mea)/Tk,2,mod

(47)

β=(wi,mod-wi,mea)/wi,mod

(48)

式中:Tk,2,mea和Tk,2,mod分别表示第i级床层出口的温度实测值(℃)和模型计算值(℃)；wi(i=1，2，…，6)表示产品气体、轻石脑油、重石脑油、航煤、柴油和尾油的质量分数实测值(%)和计算值(%)。

选用另外第1～10 d的第2组的测量数据代入加氢裂化反应器模型计算，结果见图7和图8，其中，RRHC表示建立的严格反应热模型；ERHC表示恒反应热假设模型；GA表示基于总误差最小用GA计算模型参数；NSGA-II表示基于双误差最小用NSGA-II计算模型参数。

3.3.1 加氢裂化反应器反应床层出口温度

从图7可以看出：除No.1和No.2床层外，RRHC+NSGA-II的计算结果明显优于其他方法。而其中No.4和No.6床层的β值更低，低至±0.08%。至于No.1和No.2误差稍大的原因推测是其中主要发生加氢精制反应，与假设6个床层均发生一级裂化反应有差异。事实上，1、2号床层的β值也只有±3.52%，综合平均相对误差更只有1.59%。

RRHC—Rigorous reaction heat model；ERHC—Empirical reaction heat model；GA—Calculation based on minimum total error with GA；NSGA-Ⅱ—Calculation based on minimum both two errors with NSGA-Ⅱ图7 加氢裂化反应器反应床程出口温度预测误差Fig.7 Error of hydrocracking reactor bed outlet temperatures between measured and calculated(a)No.1 bed exit temperature prediction error;(b)No.2 bed exit temperature prediction error;(c)No.3 bed exit temperature prediction error;(d)No.4 bed exit temperature prediction Error;(e)No.5 bed exit temperature prediction error;(f)No.6 bed exit temperature prediction error

3.3.2 加氢裂化反应器新模型计算产品分布

图8给出了末级反应器出口产品分布计算误差。由图8可知：除石脑油产品外，RRHC+NSGA-Ⅱ均优于ERHC+GA和ERHC+NSGA-Ⅱ方法，相对误差仅± 6.94%。比如航煤产品，其新建加氢裂化反应器模型的相对误差从7.64%降至1.04%。

RRHC—Rigorous reaction heat model；ERHC—Empirical reaction heat model；GA—Calculation based on minimum total error with GA；NSGA-II—Calculation based on minimum both two errors with NSGA-Ⅱ图8 产品分布预测误差Fig.8 Error of products distribution between the measured and the calculated(a)Forecast error of gas products;(b)Forecast error of light naphtha products;(c)Forecast error of heavy naphtha products;(d)Forecast error of jet fuel products;(e)Forecast error of diesel products;(f)Tail oil prediction error

3.3.3 加氢裂化反应器新模型计算反应热

图9展示了利用集总标准燃烧热法和定热值法(2.1×104kJ/kg H2)计算得到的集总反应热分布。由图9可见，随着集总平均摩尔质量变大，定值法先降后升，燃烧热法则是头高、中平、末低。换言之，定值法轻集总反应放热多，燃烧热法中间集总贡献大。此外，燃烧热法中No.22集总反应热是负值，可能为吸热。

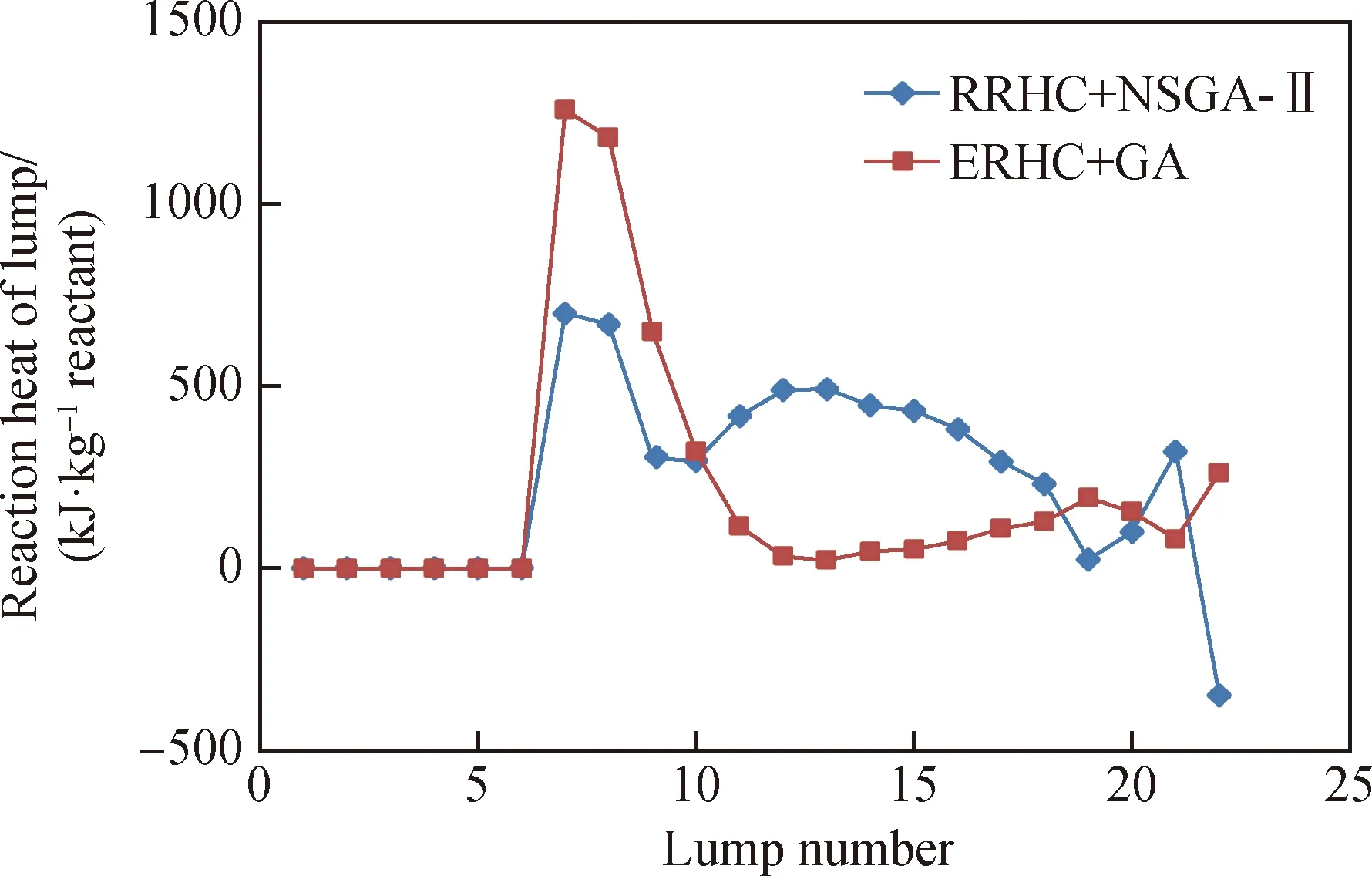
RRHC—Rigorous reaction heat model；ERHC—Empirical reaction heat model；GA—Calculation based on minimum total error with GA；NSGA-Ⅱ—Calculation based on minimum both two errors with NSGA-Ⅱ图9 集总反应热计算结果Fig.9 Calculation results of lumps reaction heat

表7综合给出了加氢裂化反应器新旧模型应用案例各反应床层出口温度和反应产物组成的计算结果。

由表7可见，采用新的Chevron模型后，反应温度和产品分布预测准确分别提高0.4%和3.5%；采用新的Chevron模型及NSGA-Ⅱ参数拟合方法后，产品分布预测精度提高14.0%。

表7 加氢裂化反应器新旧模型应用案例各反应床层出口温度和反应产物组成的计算结果Table 7 Calculation results of outlet temperature and product composition of each reaction bed in hydrocracking reactor application case of old and new models

续表

3种方法的迭代次数和迭代时间(Intel(R)Core(TM)i5-3230M CPU@2.60 GHz，安装内存(RAM)：8.00 GB)的对比如图10所示。由图10可知：采用新的Chevron模型及新的参数拟合方法后迭代时间缩短。

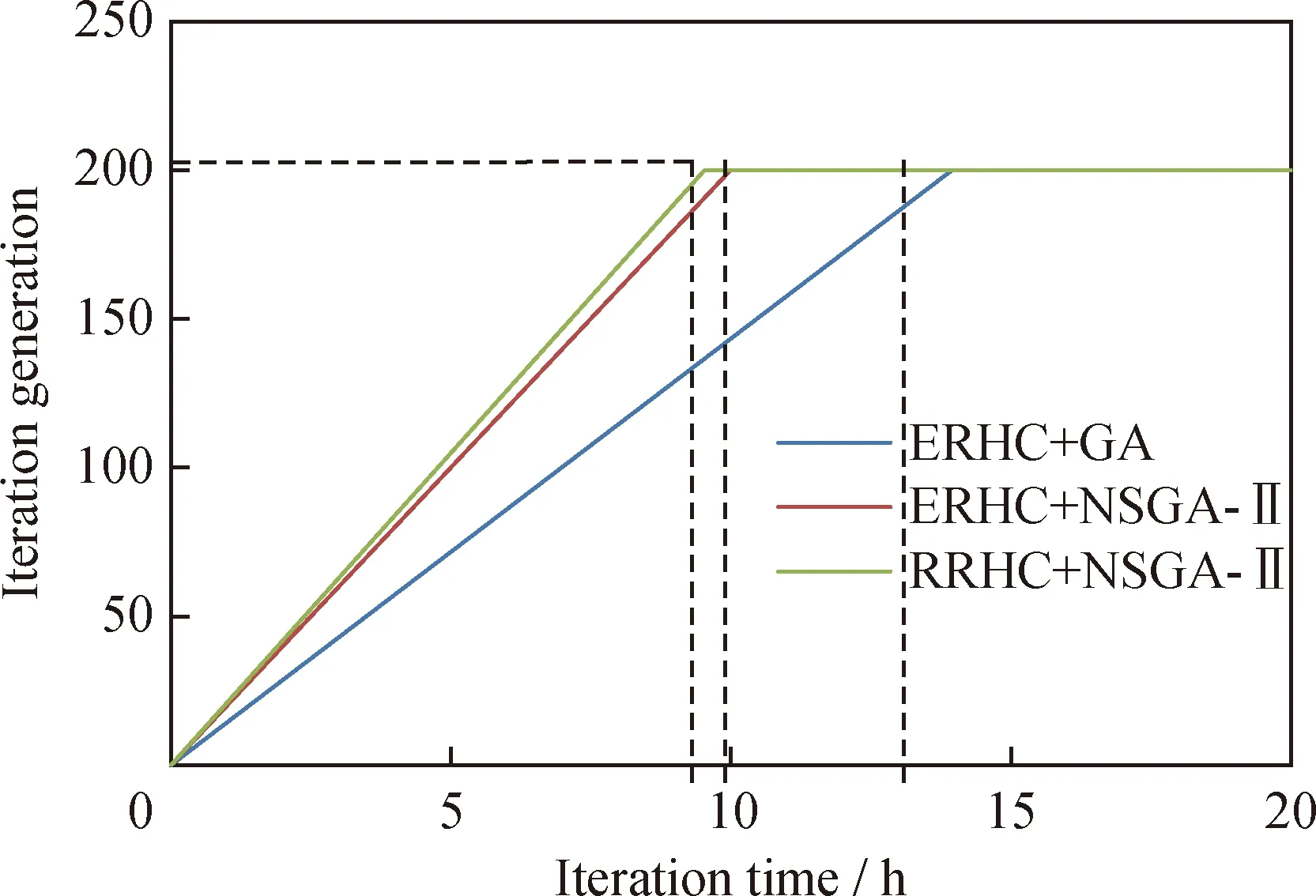
图10 加氢裂化反应器模型参数拟合迭代过程示意Fig.10 Diagram of hydrocracking reactor model iteration process

4 结 论

(1)改进了石油馏分离散集总加氢裂化Chevron反应动力学模型。其中用反应物和反应产物集总标准标准燃烧热计算反应热，取消了原模型反应热为常数(2.1×104kJ/kgH2)，与反应条件和反应体系无关的假设。

(2)在加氢裂化反应器模型参数E、K0、A、B、D、ω计算中，以反应温度误差和产品分布误差同时最小为计算原理，以多目标遗传算法(NSGA-Ⅱ)为计算方法，相较以反应温度和产品分布总误差最小为计算原理的传统方法，所得的模型参数更为准确。

(3)某加氢裂化装置反应器系统应用表明，采用新的Chevron模型后，反应温度和产品分布预测准确分别提高0.4%和3.5%；采用新的Chevron模型及新的参数拟合方法后，反应温度和产品分布预测准确分别提高-0.3%和14.0%。