一类平面分段线性Hamilton系统在线性扰动下极限环个数的估计

赵凌燕，李宝毅，张永康

（1.空军预警学院，武汉430019；2.天津师范大学 数学科学学院，天津300387）

1 引言和主要结论

分段光滑动力系统不仅能描述某些自然物理过程，而且在机械工程、航空航天等众多领域有广泛应用.平面分段线性系统是一类重要的分段光滑动力系统，对其扰动系统极限环个数的估计受到相关学者的关注.关于平面分段线性系统的研究最早见于文献[1].之后，文献[2-3]证明了当平面被一条直线分为2个区域时，连续分段线性系统最多只有1个极限环.文献[4-8]研究了不连续平面分段线性系统极限环个数的情况.文献[9]研究了当平面被从原点出发的2条射线分为2个区域时，一类平面分段线性Hamilton系统在多项式扰动下极限环的个数.文献[10]证明了当平面被分为4个区域时，一类平面分段光滑线性系统可以存在5个极限环.文献[11]研究了平面被分为2个区域时，Bogdanov-Takens系统在分段n次多项式扰动下极限环个数的上确界.文献[12]研究了一类多项式扰动下分段光滑近Hamilton系统极限环个数的上界.此外，也有研究考虑了一些二次分段系统的扰动问题[13-14].

本文考虑从原点出发的2m-1（m≥2）条射线l0，l1，…，l2m-2将平面分为2m-1个区域，射线lk-1与lk所夹的开区域记为Dk，k=1，2，…，2m-1.令l2m-1=l0，记D1*=D1∪l1，Dk*=Dk∪lk{（0，0）}，k=2，3，…，2m-1.考虑如下平面分段光滑Hamilton系统的扰动系统

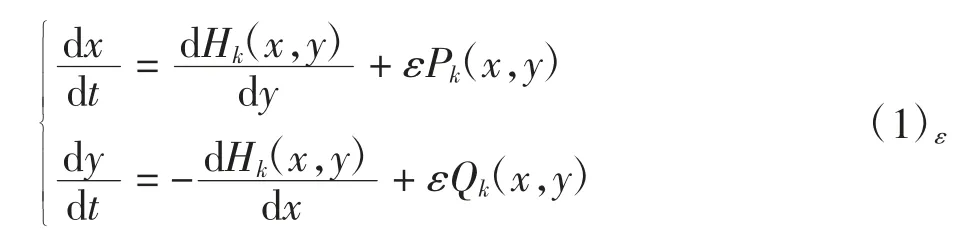
其中：0＜ε≪1；Hk（x，y）是Dk*上的二次实系数多项式；Pk（x，y）和Qk（x，y）是Dk*上的一次实系数多项式，

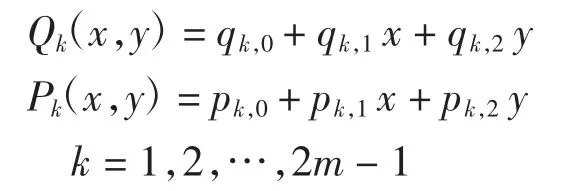
当k=0，1，…，m-1时，射线lk的参数方程为

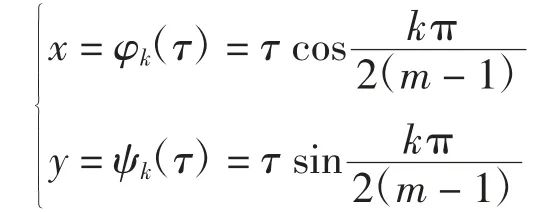
当k=m，m+1，…，2m-2时，射线lk的参数方程为

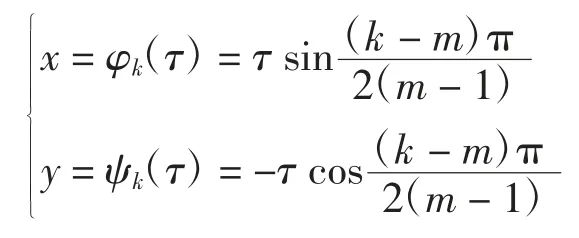
其中τ∈[0，+∞）.

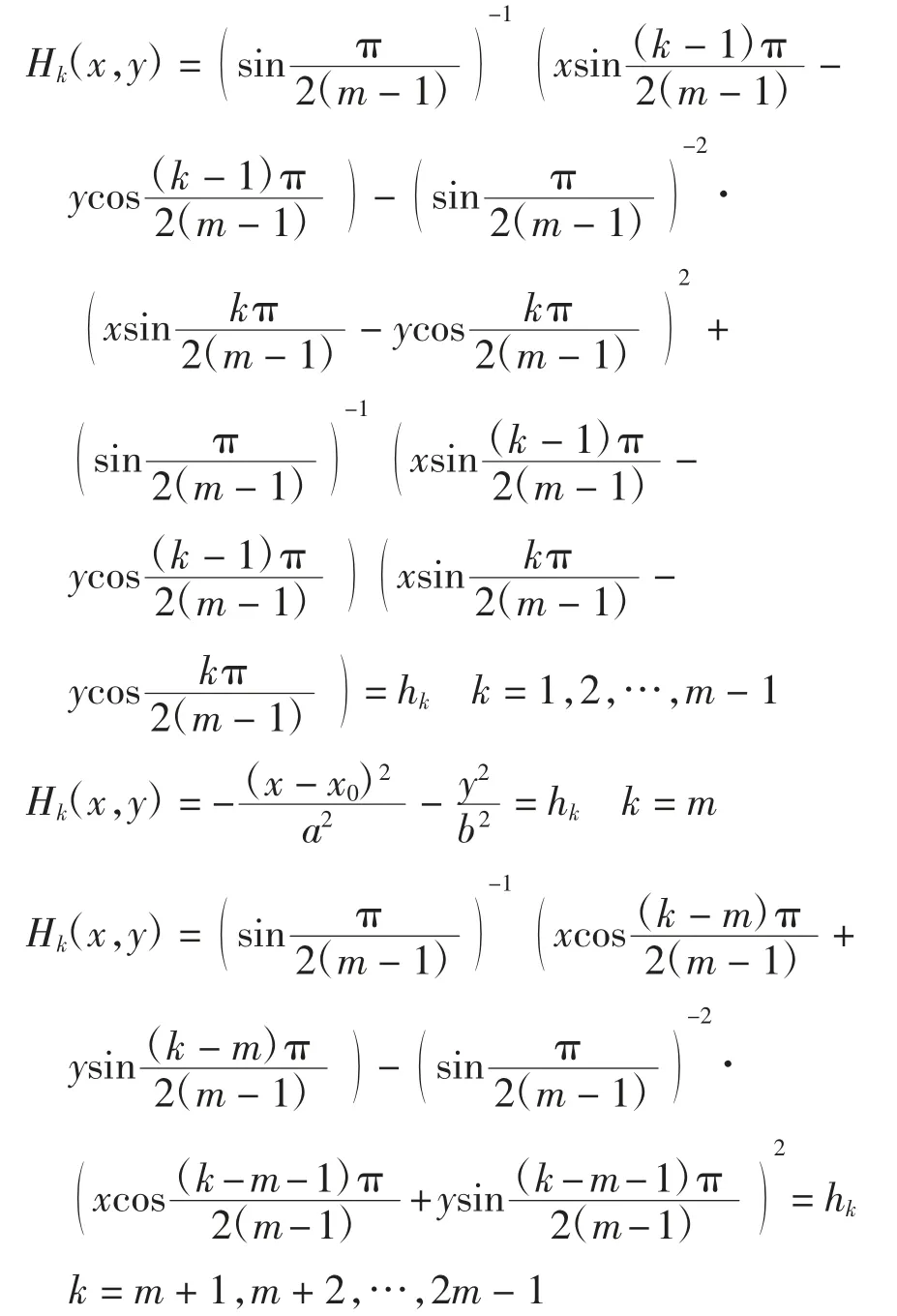
其中：a、b∈R+，x0＜0.

当ε=0时，系统（1）0存在2种周期闭轨族，一种是左半平面内的周期闭轨族，另一种是围绕原点的周期闭轨族.当m=2时，2种周期闭轨族的示意图分别见图1和图2.

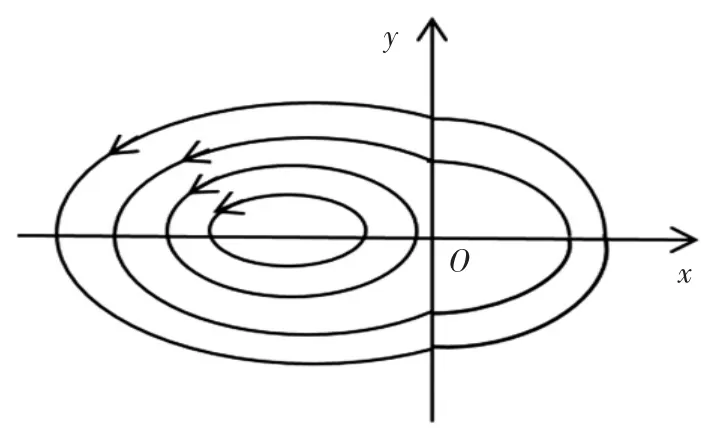
图1 左半平面内的周期闭轨族Fig.1 Periodic closed orbits in the left half plane

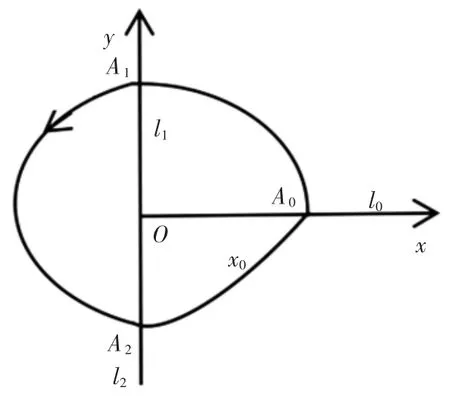
图2 围绕原点的周期闭轨族Fig.2 Periodic closed orbits around the origin

本文考虑围绕原点的周期闭轨族Γh.设

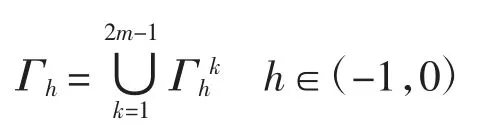
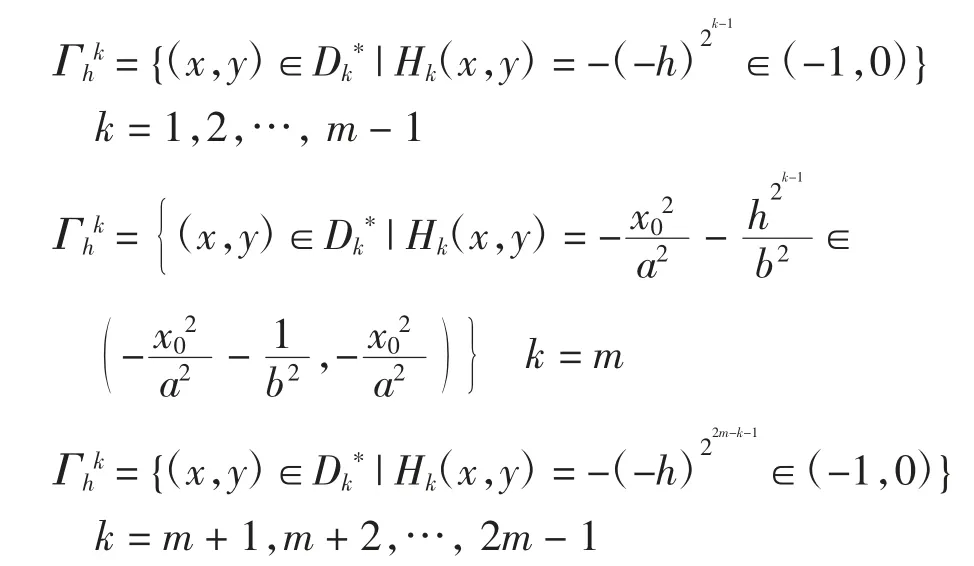
本文得到如下结论.

定理存在一次实系数多项式Pk（x，y）和Qk（x，y），使得分段线性系统（1）ε至少存在3m个极限环，其中：m≥2，k=1，2，…，2m-1.

2 一阶Melnikov函数

由文献[10]，利用数学归纳法可证明引理1成立.

引理1系统（1）ε的一阶Melnikov函数为

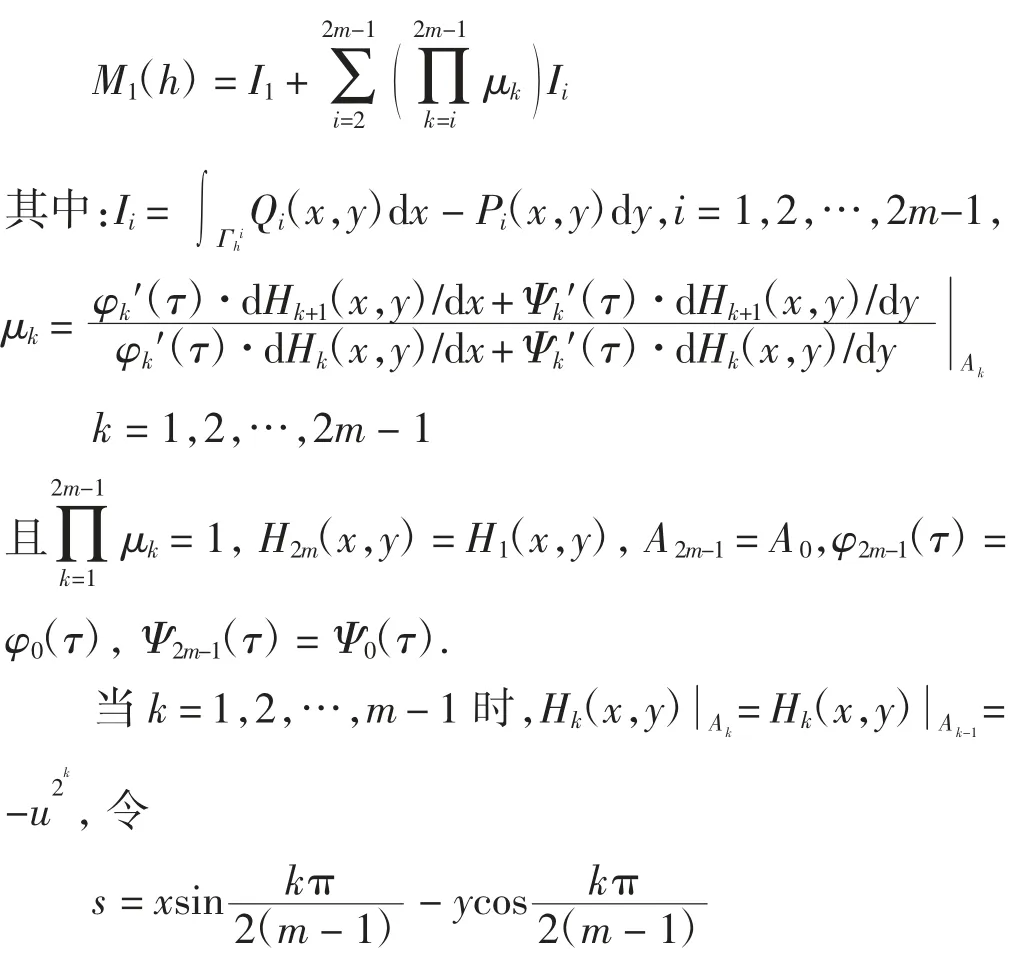
则Γhk的参数方程可写为

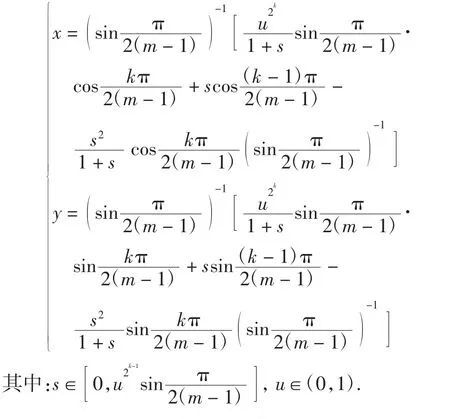
引理2对于系统（1）ε，当k=1，2，…，m-1时，

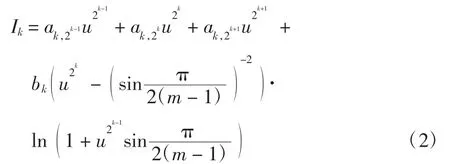
其中：

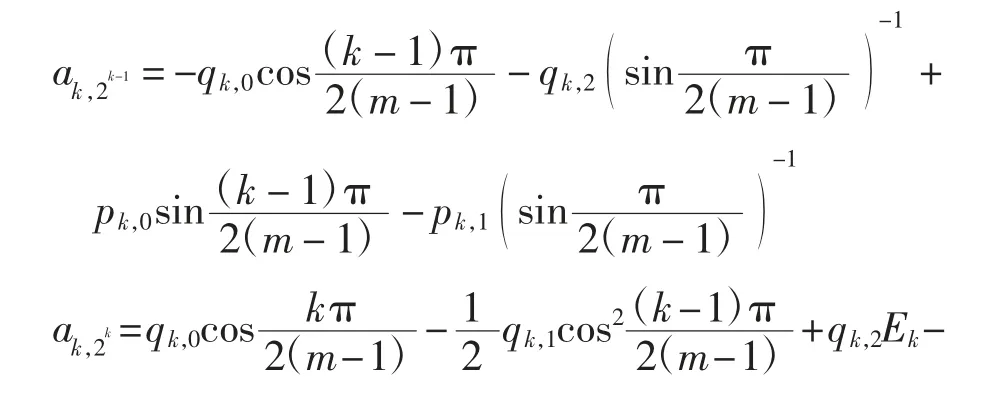
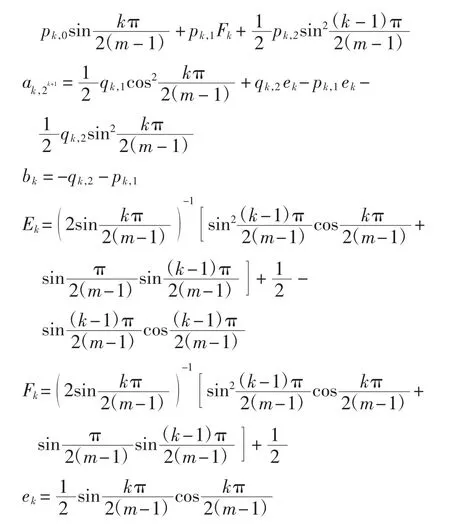
且ak，2k-1、ak，2k、ak，2k+1、bk对于qk，0、qk，1、qk，2、pk，0、pk，1、pk，2相互独立，

证明当k=1，2，…，m-1时，

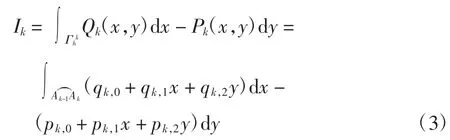
计算得

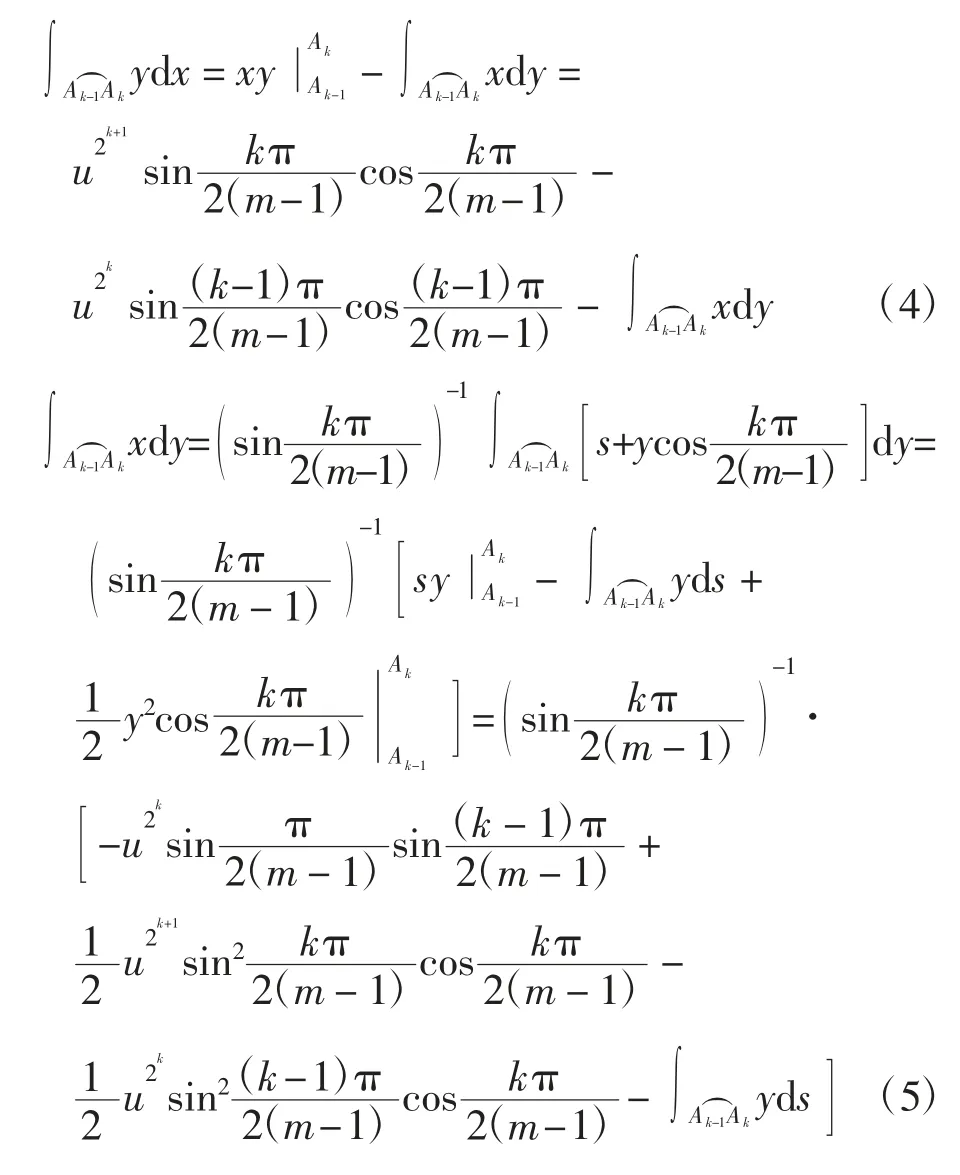
利用Γhk的参数方程可得

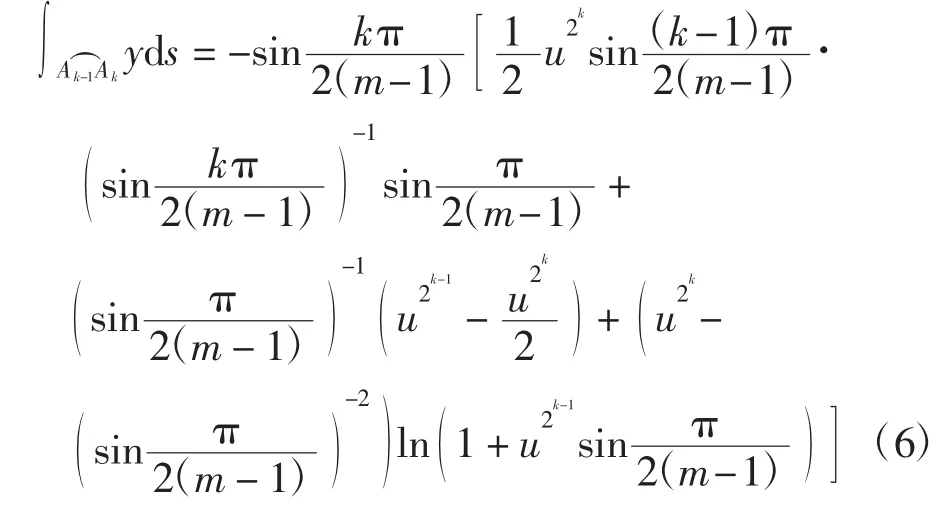
将式（4）~式（6）代入式（3），经化简可得式（2）成立.

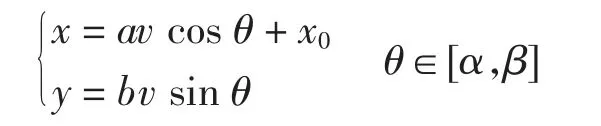
其中：α为Γhm位于Am-1（0，u2m-1）时所对应的角，即cosα=为Γhm位于Am（0，-u2m-1）时所对应的角，即

引理3对于系统（1）ε，

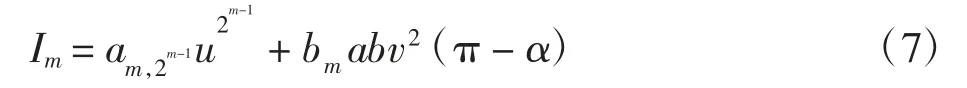
其中：am，2m-1=x0qm，2+2pm，0+x0pm，1，bm=-qm，2-pm，1，且am，2m-1、bm对于qm，0、qm，1、qm，2、pm，0、pm，1、pm，2相互独立.

证明

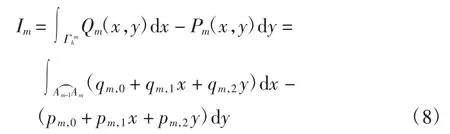
计算得

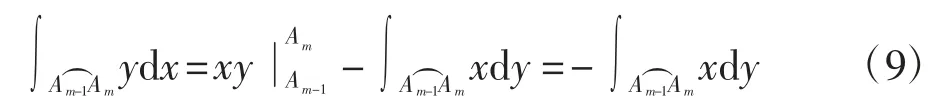
利用Γhm的参数方程可得

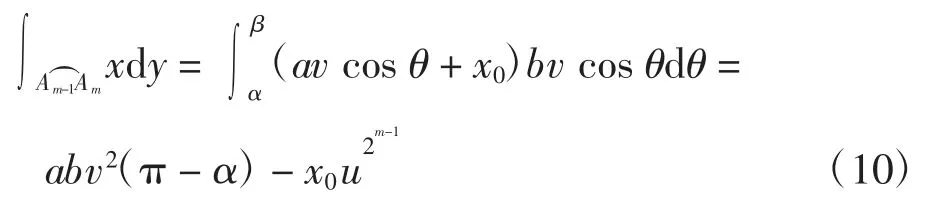
将式（9）~式（10）代入式（8）可得式（7）成立.

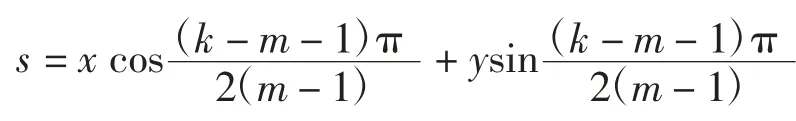
则Γhk的参数方程可写为

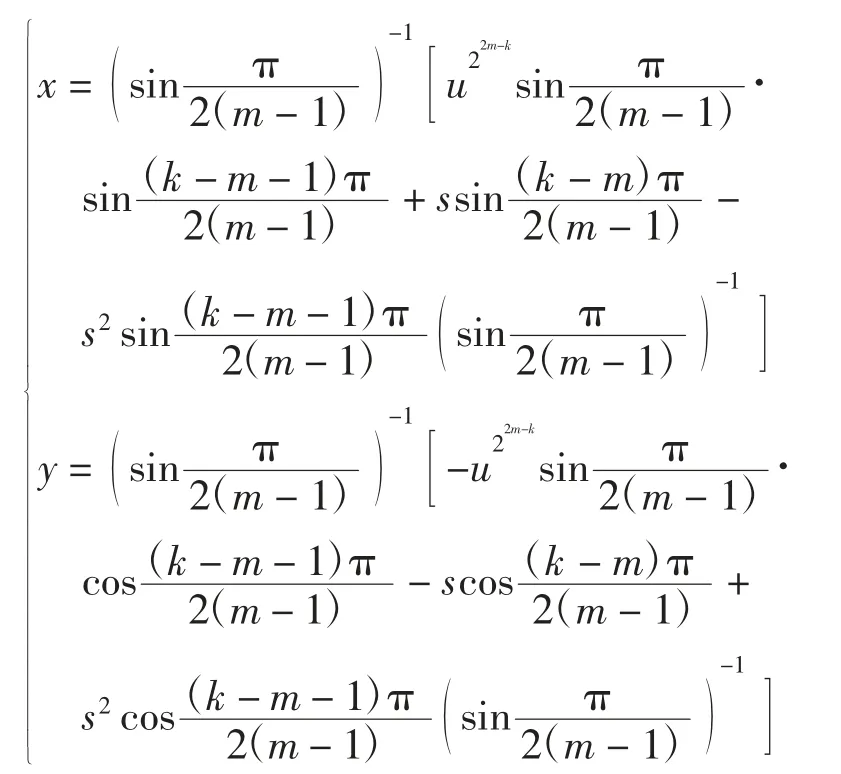
引理4对于系统（1）ε，当k=m+1，m+2，…，2m-1时，

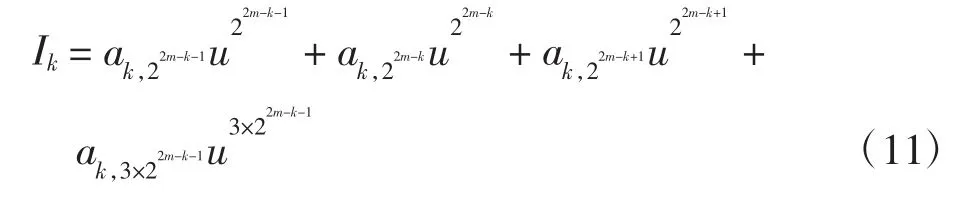
其中：

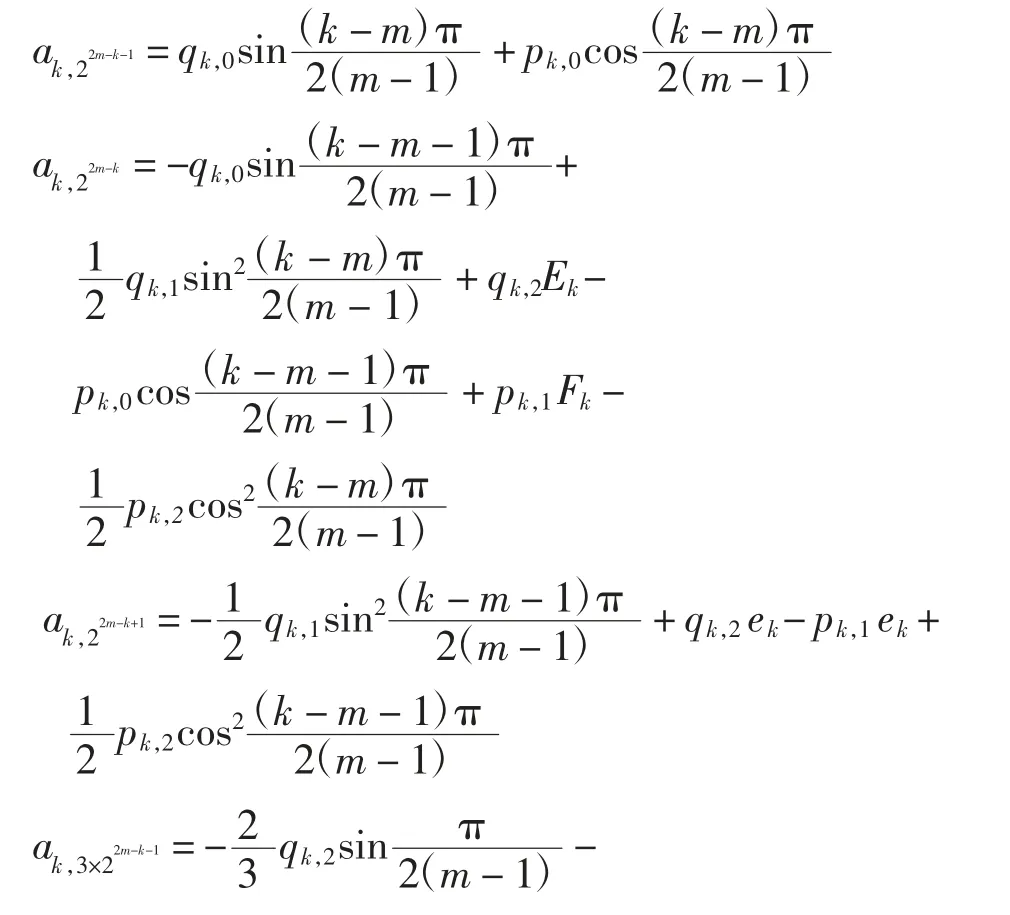
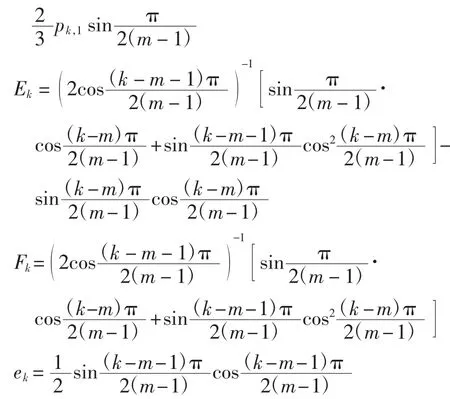
且ak，22m-k-1、ak，22m-k、ak，22m-k+1、ak，3×22m-k-1对于qk，0、qk，1、qk，2、pk，0、pk，1、pk，2相互独立.

证明当k=m+1，m+2，…，2m-1时，

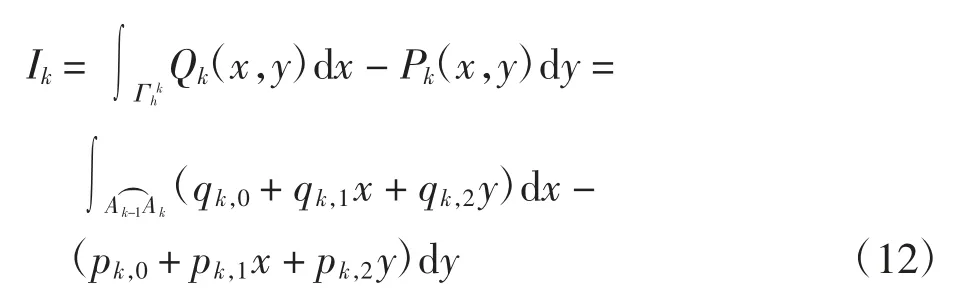
计算得

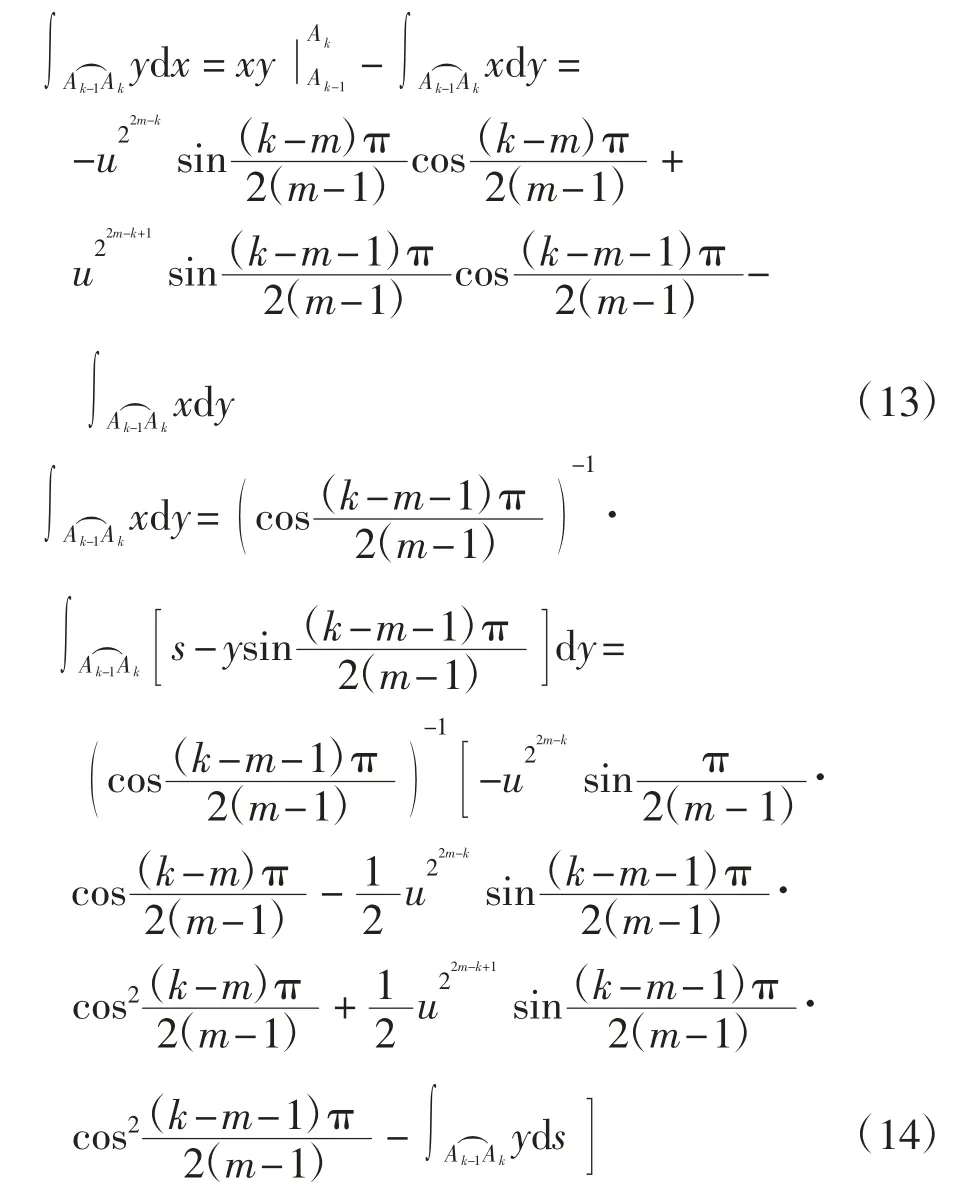
利用Γhk的参数方程可得

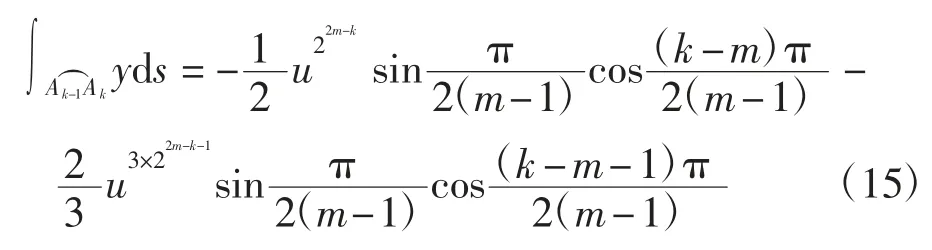
将式（13）~式（15）代入式（12）可得式（11）成立.

3 一阶Melnikov函数变号零点的个数

引理5[9]设f（u）和g（u）是R+上的连续函数，当0＜u≪1时，

其中fm·gl≠0.若f（u）在R+上存在k个变号零点，且l＜m，则存在实数C，使得F（u）=f（u）+Cg（u）在R+上至少存在k+1个变号零点.

由引理5可得如下推论.

推论[9]设φi（u）是R+上的连续函数，当0＜u≪1时，φi（u）=Aiuαi+o（uαi），Ai≠0，α1＜α2＜…＜αk，则存在实数Ci，i=1，2，…，k，使得上至少存在k-1个变号零点.

定理的证明当k=1，2，…，m-2时，计算得

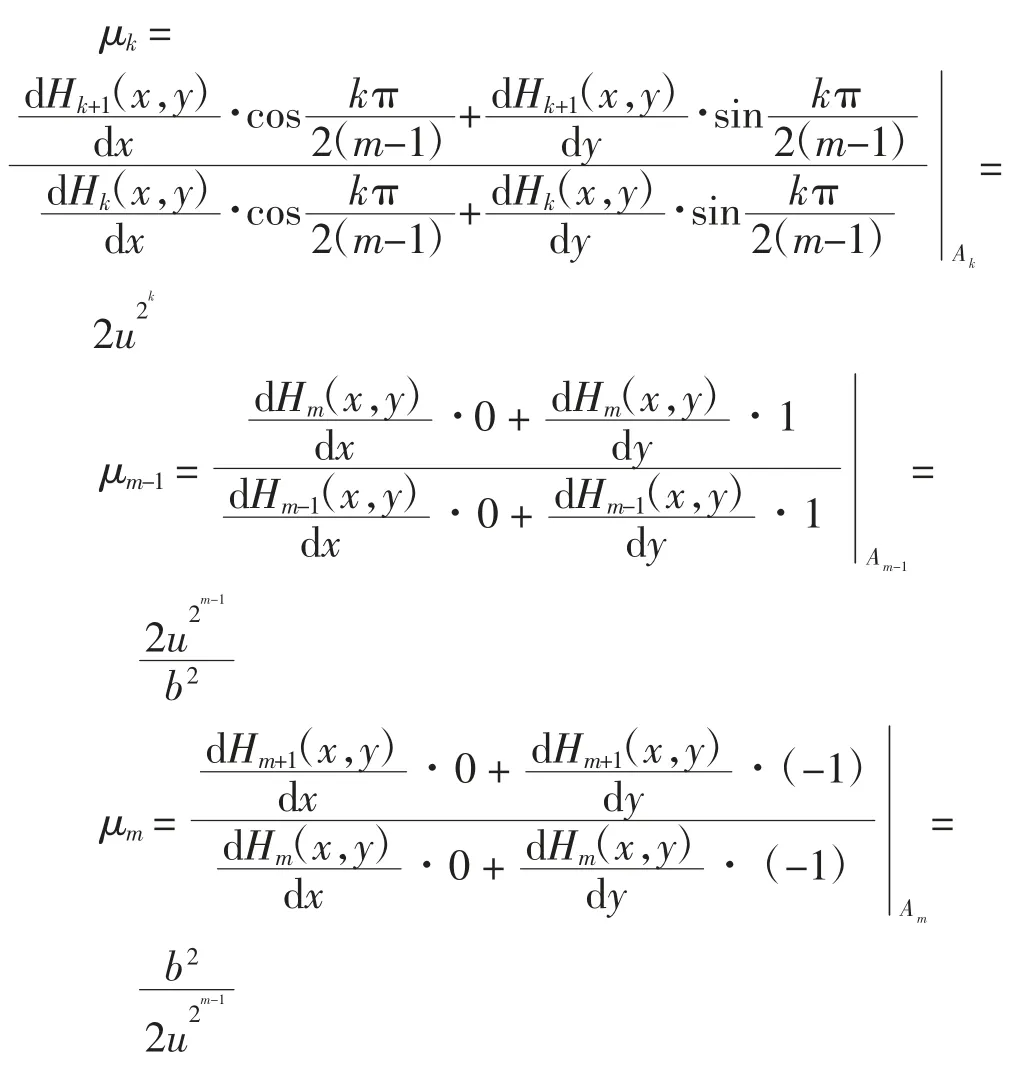
当k=m+1，m+2，…，2m-2时，计算得

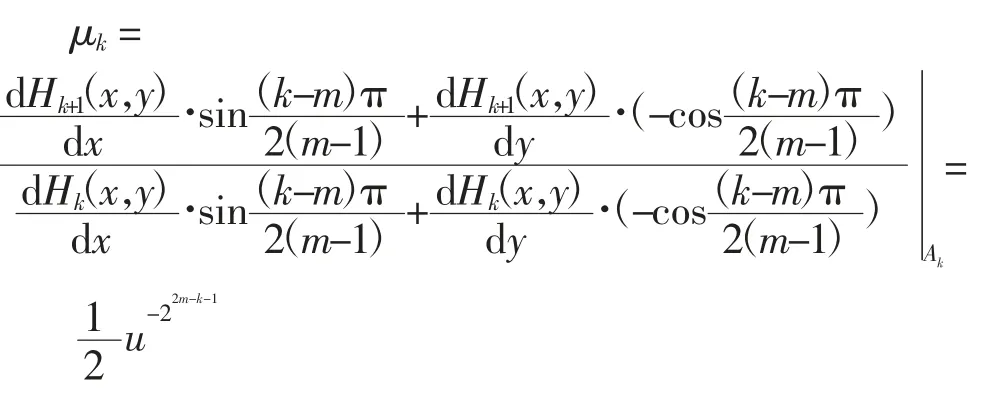
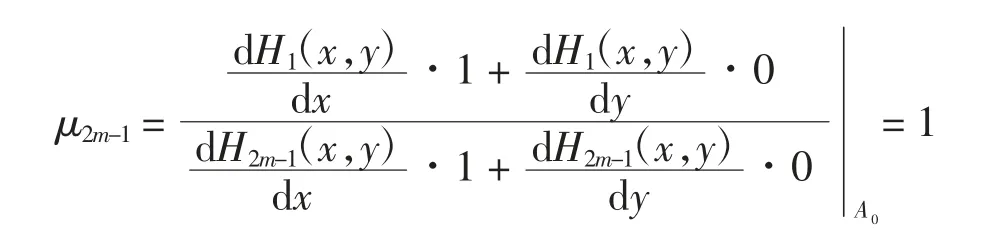
由μk，k=1，2，…，2m-1的计算结果及引理1~引理4可得系统（1）ε的一阶Melnikov函数为

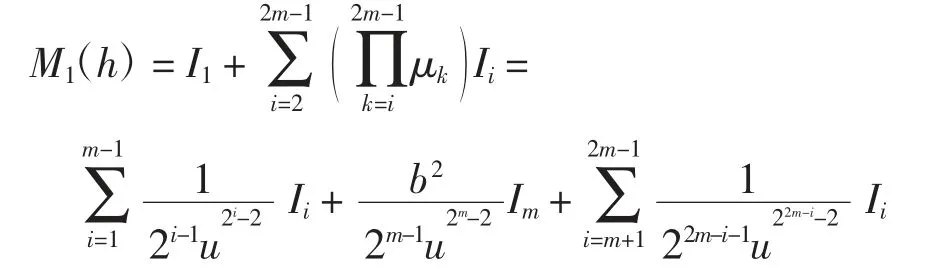
当i=m+1，m+2，…，2m-1时，因为

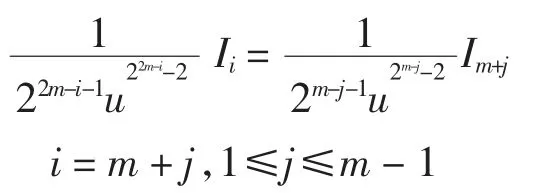
因此有

其中：多项式中u的次数模3同余1或0，

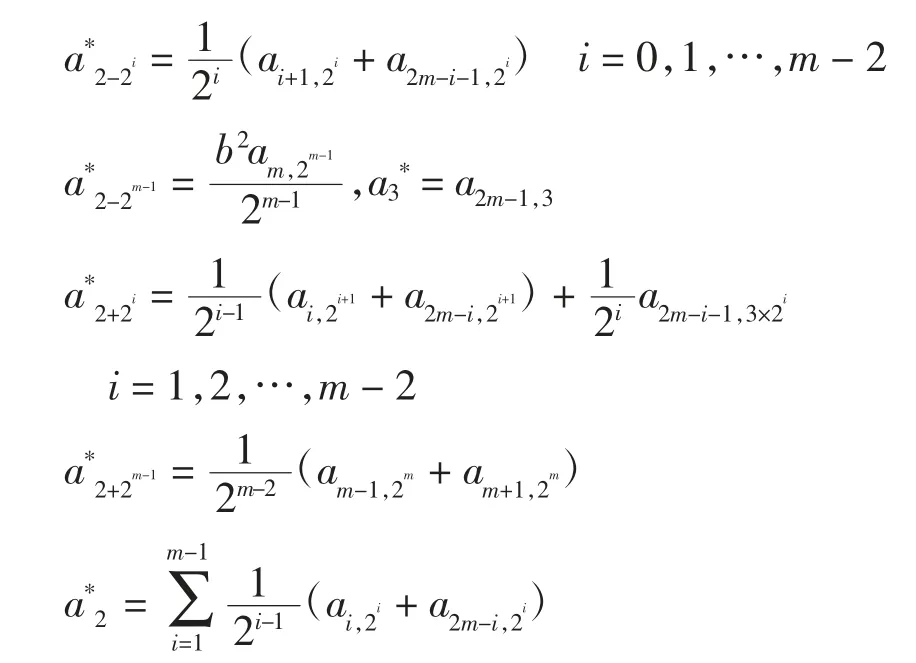
当i=1，2，…，m-1时，由Taylor展开式可得

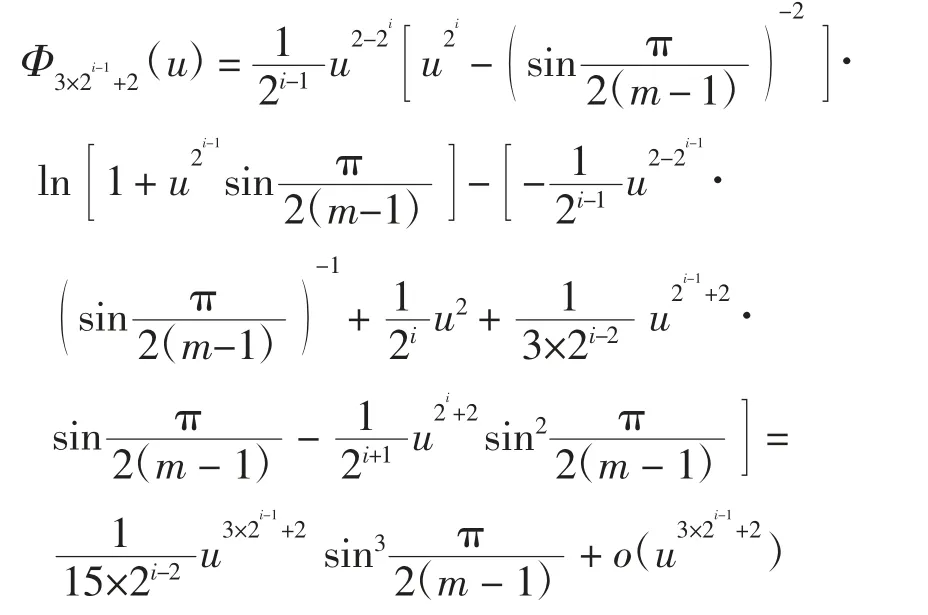
则Φ3×2i-1+2（u），i=1，2，…，m-1中u的最低次数模3同余2.

当u→0+时，因为0+，所以α→0+，故π-α→π-，此时有

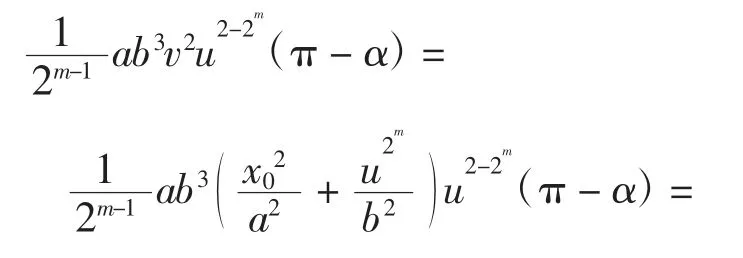
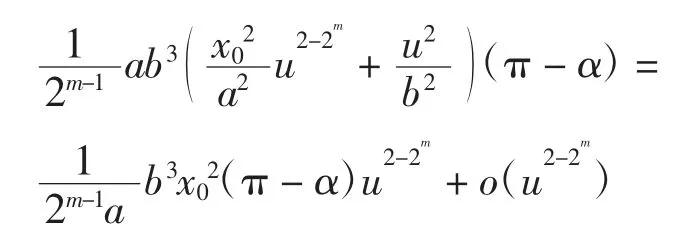
综上可得

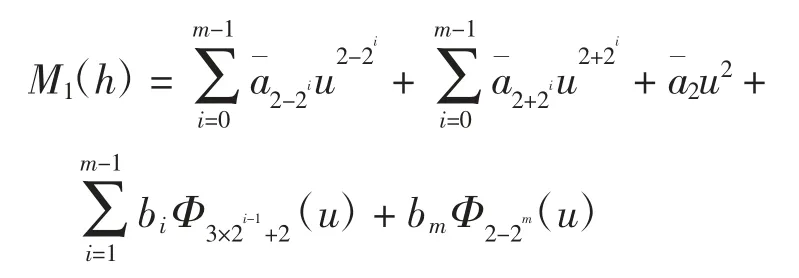
其中：

故M1（h）=0等价于

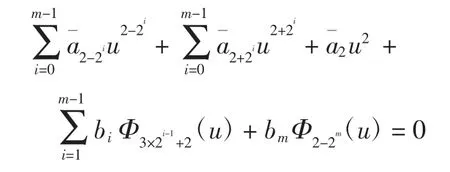
由推论可知，M1（h）至少存在3m个变号零点，即系统（1）ε至少存在3 m个极限环.定理证毕.