高速铁路夕发朝至卧铺列车始发终到 时间域计算方法研究
杨静伟,耿 放,刘宁馨,安 迪,孙 毅,李琨浩
(1.河北轨道运输职业技术学院 城市轨道交通系,河北 石家庄 052165;2.河北轨道运输职业技术 学院 铁道运输系,河北 石家庄 052165;3.中国铁道科学研究院集团有限公司 运输及经济研究所, 北京 100081;4. 中国铁路北京局集团有限公司 石家庄站,河北 石家庄 050051)
0 引言
高速铁路卧铺动车组列车的开行主要有日行和夜行2类,目前我国是以夜行为主,即高速铁路夕发朝至卧铺动车组列车(以下简称“高速铁路夕发朝至列车”)。由于此类列车开行与高速铁路综合维修天窗设置之间存在冲突,因而如何优化列车开行与综合维修天窗设置之间的关系,为高速铁路夕发朝至列车开行方案提供编制依据,以满足旅客出行需求和优化运力资源配置,是国内学者对高速铁路夕发朝至列车运输组织研究的重点领域[1-3]。
高速铁路夕发朝至列车的始发终到时间域,主要基于高速铁路夕发朝至列车的定义、旅客选择偏好及客运产品运营经验等,不同研究中的取值也有所不同,徐长安等[1]和林枫[4]将始发和终到时间域分别定义为19 : 00—23 : 00,6 : 00—10 : 00;于婕等[5]定义为18 : 00—24 : 00,6 : 00—11 : 00;刘敏等[6]定义为19 : 00—22 : 00,6 : 00—9 : 00。由于目前研究多将高速铁路夕发朝至列车的始发终到时间域作为已知条件来考虑,很少对该时间域的计算方法进行研究。因此,亟需结合高速铁路夕发朝至列车开行与综合维修天窗设置现状,创新高速铁路夕发朝至列车始发终到时间域计算方法,以进一步提高列车运行图编制质量,为高速铁路夕发朝至列车开行与天窗设置的协同优化提供理论支撑。
1 高速铁路夕发朝至列车与天窗关系分析
1.1 问题描述
从2019年高速铁路夕发朝至列车的开行情况来看,高速铁路夕发朝至列车运行距离集中在 1 400 ~ 2 400 km之 间,历 时 集 中 在10 ~ 15 h之间。其中,160 km/h速度等级的夕发朝至列车运行距离在1 100 ~ 2 400 km之间,历时在9 ~ 22 h之间,旅行速度在100 ~ 125 km/h之间;250 km/h速度等级的高速铁路夕发朝至列车运行距离在800 ~ 2 800 km 之间,历时在8 ~ 13 h之间,旅行速度在100 ~ 220 km/h 之间。天窗的开设方式主要有2种,分别是垂直矩形天窗和分段矩形天窗[7];列车开行模式也分为2种,分别是全高速线运行模式和“天窗时段下线”运行模式,全高速线运行模式即夜行列车利用高速铁路线运营的模式,例如北京—广州/深圳方向、上海/杭州—广州/深圳方向等开行的列车;“天窗时段下线”运行模式即夜行列车在天窗时间段利用与高速铁路平行既有线运营的模式,与高速铁路天窗不产生冲突[7-8]。
全高速线运行模式由于列车开行和天窗设置间存在相互制约关系,不易通过传统计算方法确定列车合理始发终到时间域。通过分析列车运行图特征,按时间顺序将高速铁路区段各区间视为相互联系的多个决策阶段,将区段内各站的列车到达和出发时刻视为下一阶段的决策集合,满足区间天窗开设时长约束的决策视为决定当前阶段状态的最优决策,且各阶段状态具备无后效性的特征。因此,可将开设分段矩形天窗、全高速线运行模式下的高速铁路夕发朝至列车的始发终到时间域计算,转化为确定性的定期多阶段决策问题,通过输入停站方案和各阶段天窗开设时长要求,输出合理列车始发终到时间域。
1.2 列车运行线与天窗关系分析
成对开行的高速铁路夕发朝至列车,在全高速线运行模式下,按照天窗照顾行车的原则,根据天窗与运行线在运行图中的相对铺画位置,参考京广高速铁路(北京西—广州南)[3],分段矩形天窗的设置可分为4个区域。分段矩形天窗设置区域如图1所示,阴影部分为运行线铺画区域,Ⅰ,Ⅱ,Ⅲ,Ⅳ为分段矩形天窗的设置区域。
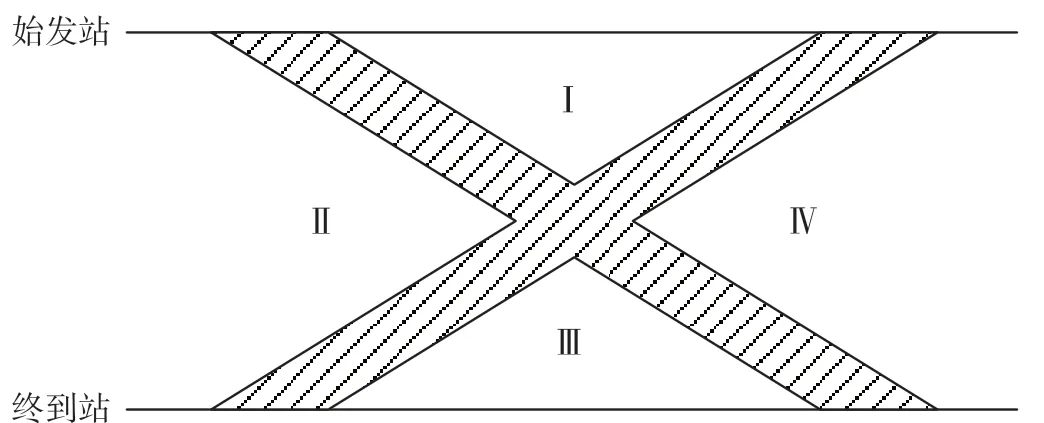
图1 分段矩形天窗设置区域Fig.1 Segmented rectangular maintenance window area
运行图中各区域内天窗与运行线的相对位置如图2所示,可细化为6种情况(阴影部分为天窗,Sk-1和Sk为车站编号)。其中,情况b和情况d也包括列车通过该区间后,分别在Sk站和Sk-1站产生停站需求,但此时,列车的停站不受天窗开设区域的制约,因而不做考虑。
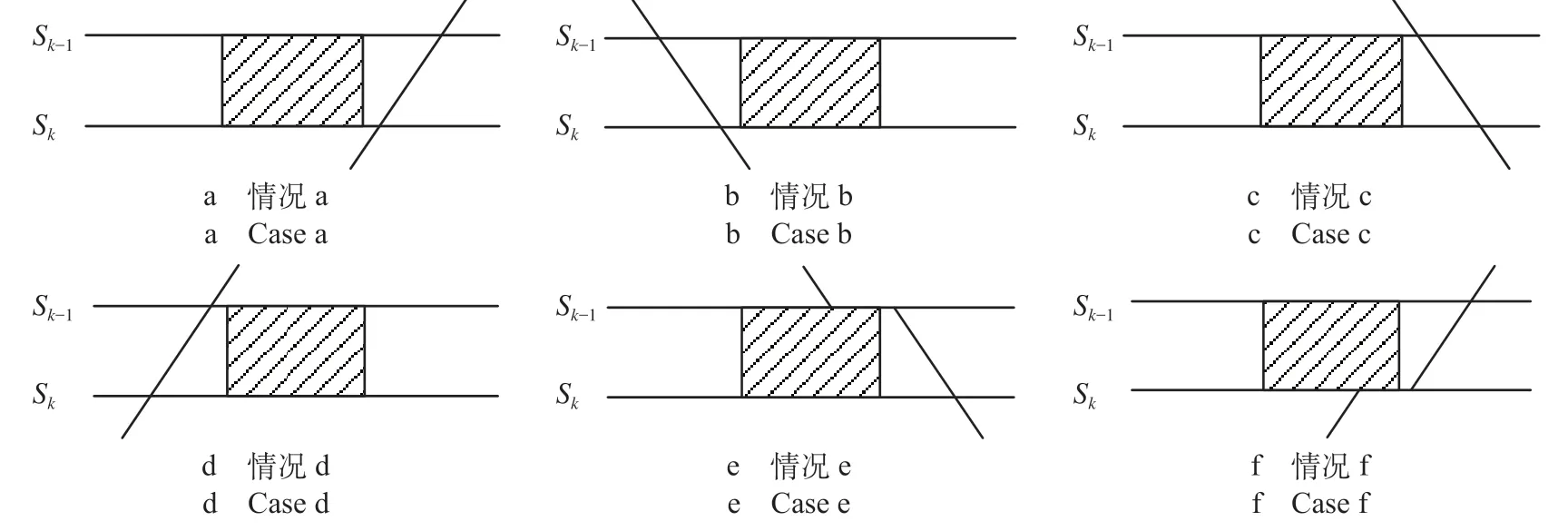
图2 各区域内天窗与运行线的相对位置Fig.2 Relative position of train operation line and maintenance window in each area
通过对列车运行图特征的分析,各区域内天窗与运行线相对位置的可能情况如表1所示。

表1 各区域内天窗与运行线相对位置的可能情况Tab.1 Possible relative position of train operation line and maintenance window in each area
由此可知,在给定天窗开设时段的情况下,运行线的铺画区域和天窗的开设区域存在一定的制约关系,具体表现为:①运行线铺画区域越宽,天窗允许开设区域越小,即始发终到时间域的范围与天窗允许开设时长呈负相关关系;②在高速铁路夕发朝至列车开行日的运行线铺画区域,必须保证该分段天窗开设时长的最低要求。
2 高速铁路夕发朝至列车始发终到时间域计算模型
将高速铁路按区间划分阶段,各阶段开始时的下行列车到达时刻范围和上行列车出发时刻范围表示该阶段的状态及决策集合,初始化的始发终到时间域为边界条件,各阶段天窗开设时长为约束条件,总天窗收益最大为优化目标,构建动态规划模型。
2.1 模型假设及变量参数设置
为了便于最后计算结果呈现,模型构建基于以下假设:①列车的开行符合先发先到特征;②分段矩形天窗的分段情况为已知条件;③各区间天窗开始前的安全间隔时间固定,各区间天窗结束后的确认列车运行时间为按技术速度计算的该区间运行时分;④停站方案已知。
设S为车站集合,k为车站和阶段索引,第k阶段代表Sk-1至Sk区间,k∈{2,…,m};i为列车索引,i∈{1,n};R和ω为分段矩形天窗在运行图中的4个分布区域集合,记R= {Ⅰ/Ⅲ,Ⅱ,Ⅳ},ω∈ {Ⅰ,Ⅲ,Ⅱ,Ⅳ}。模型相关符号及含义如表2所示。
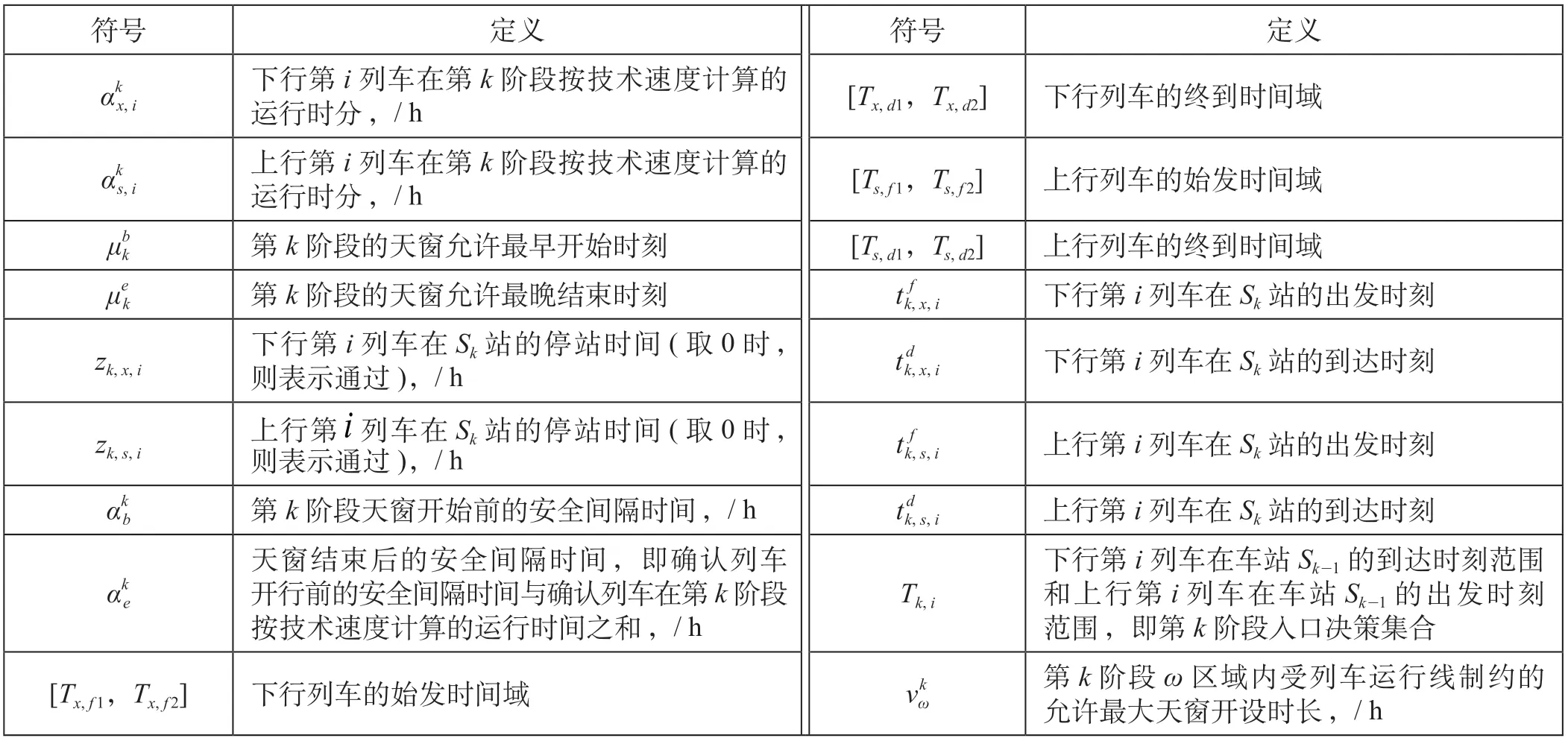
表2 模型相关符号及含义Tab.2 Related symbols and meanings of the model
2.2 模型构建
每个阶段的天窗开设时长应满足相应标准。如京广高速铁路在高速铁路夕发朝至列车开行日,采取大小天窗结合并用的模式[7],大天窗满足4 h综合维修天窗的要求,小天窗时长压缩至3 h左右。定义“天窗收益”表示各阶段的决策是否满足该阶段的天窗开设时长要求,满足要求的天窗收益值取1,反之取0。
设高速铁路共开行n对高速铁路夕发朝至列车。各阶段的天窗收益,取决于本阶段前后2个车站的上下行第1列车(先发列车,下同)和第n列车(后发列车,下同)的出发及到达时刻,共16个关键时刻要素。第k阶段各区域的天窗收益具体如下。
第k阶段Ⅰ区域的天窗收益vIk,分别取决于下行第n列车在车站Sk的到达时刻和该阶段的天窗允许最早开始时刻(考虑天窗开始前的安全间隔时间)中的最晚时刻,以及上行第1列车在车站Sk的出发时刻和该阶段的天窗允许最晚结束时刻(考虑天窗结束后的安全间隔时间)中的最早时刻,可表示为
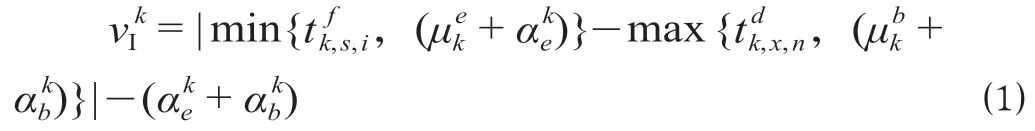
第k阶段Ⅱ区域的天窗收益,分别取决于上行第1列车在车站Sk的出发时刻和下行第1列车在车站Sk-1的出发时刻中的最早时刻,以及第k阶段的天窗允许最早开始时刻,可表示为
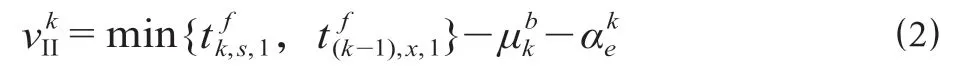
第k阶段Ⅲ区域的天窗收益,分别取决于下行第1列车在车站Sk-1的出发时刻和该阶段的天窗允许最晚结束时刻(考虑天窗结束后的安全间隔时间)中的最早时刻,以及上行第n列车在车站Sk-1的到达时刻和该阶段的天窗允许最早开始时刻(考虑天窗开始前的安全间隔时间)中的最晚时刻,可表示为
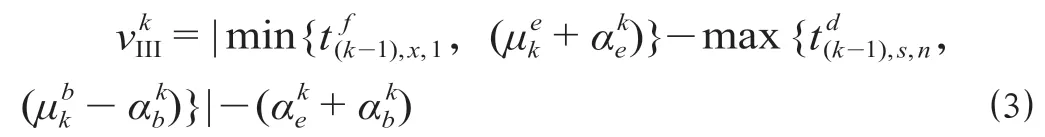
第k阶段Ⅳ区域的天窗收益,分别取决于上行第n列车在车站Sk-1的到达时刻和下行第n列车在车站Sk的到达时刻中的最晚时刻,以及第k阶段的天窗允许最晚结束时刻,可表示为
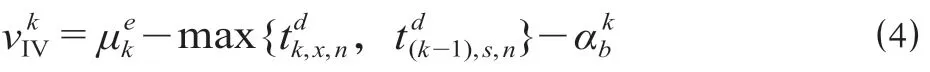
根据运行图特征分析,任一阶段中Ⅰ和Ⅲ区域的天窗收益不会同时存在,第k阶段中Ⅰ或Ⅲ区域的天窗收益VkI/III,可表示为

因此,第k阶段的最终天窗收益Vk,可表示为
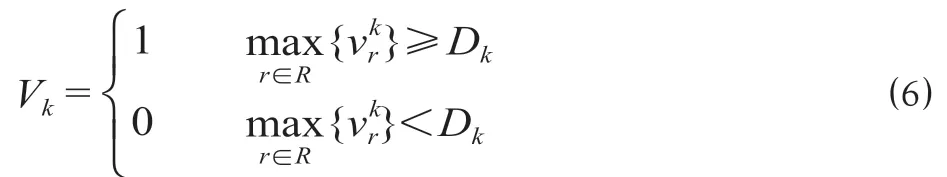
由于各阶段需保证该阶段天窗最低开设时长的要求,该多阶段决策问题存在可行解时的最终收益一定为(m- 1),对应的策略集合,即是满足分段矩形天窗开设要求的合理始发终到时间域。
考虑到各阶段的天窗开设时长,受上下行列车运行线铺画区域的共同影响,各站的8个关键时刻要素,采取下行列车的到达和出发时刻根据下行列车始发时间域正推,上行列车的到达和出发时刻根据上行列车终到时间域反推的方式。因此,Sk站的关键时刻要素递推公式为
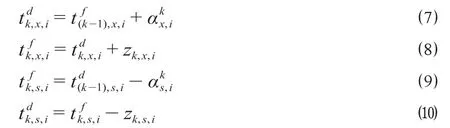
将Tk,i作为状态变量,则该确定性的定期多阶段决策问题的最优化原理为

其中,状态变量Tk,i的最优化原理为
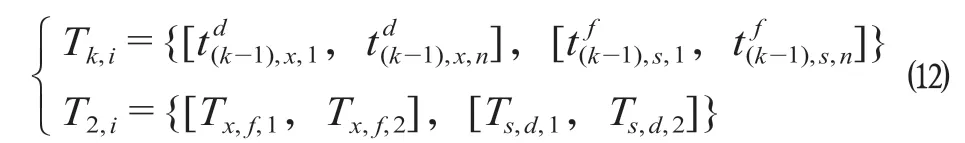
2.3 模型求解
模型的求解共需要2轮迭代计算,第一轮迭代边界条件为初始化的下行列车始发时间域和上行列车终到时间域,迭代结果为最优下行列车终到时间域和上行列车始发时间域,将这一结果作为第二轮迭代的初始条件,最终输出符合各阶段天窗开设时长要求的上下行列车始发终到时间域。具体求解过程如下。
步骤1:初始化时间格式、算法参数和边界条件。为方便计算,将参数和变量中涉及到的时刻单位统一为 h,并均加12后除以24取余。
步骤2:第一轮迭代。根据公式(7)至公式(10)通过初始化的T2,i迭代推导出S2至Sm各站的8个关键时刻要素。
步骤3:计算各阶段天窗收益。根据公式(1)至公式(6)代入步骤2的关键时刻要素,计算出本阶段允许的最大天窗开设时长,并判断是否满足本阶段的天窗开设时长要求。若满足,则返回步骤2进行下一阶段的判断;若不满足,则进入步骤4。
步骤4:更新决策集合。对于不满足本阶段天窗开设时长要求的,收缩相应的关键时刻要素所形成的出发和到达时间域范围,步长为1 min,并返回步骤3继续判断。
步骤5:第二轮迭代。通过步骤2至步骤4迭代出的车站Sm的关键时刻要素,即[Tx,d1,Tx,d2]和 [Tx,f1,Tx,f2],将其作为初始条件,代入按技术速度计算的区间运行时分和各站停车时间zk,x,i,zk,s,i,反 向 迭 代 出[Tx,f1,Tx,f2]和[Tx,d1,Tx,d2],算法结束。算法流程如图3所示。
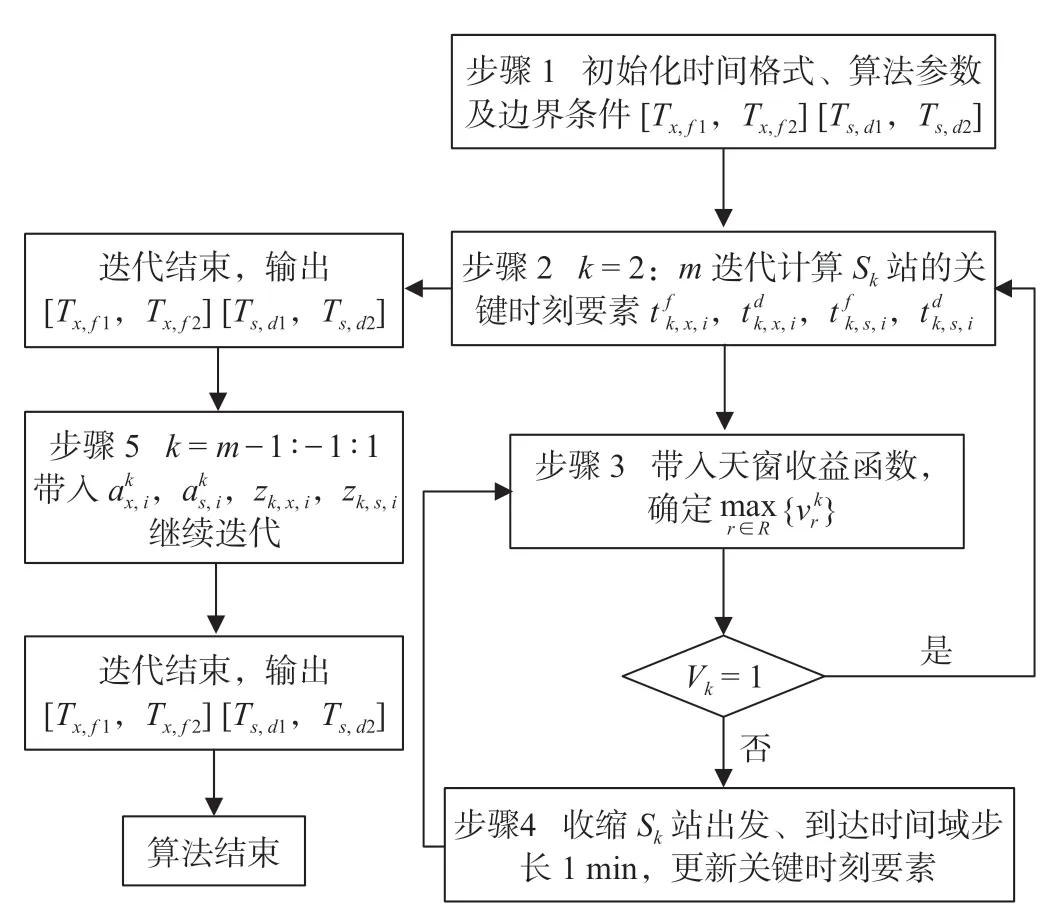
图3 算法流程Fig.3 Algorithm flow chart
3 实例研究
以京广高速铁路2021年第2季度列车运行图为基准,验证模型和算法的合理性。京广高速铁路全线共40个车站,开行7对高速铁路夕发朝至列车,其中D939和D930在京广高速线运行交路为北京西—长沙南。对2021年第2季度列车运行图数据进行先发先到处理,初始化停站方案,如上行先发列车D922次在长沙南京广场到开时间分别为22 : 52和22 : 58,停站时间为6 min,D930在长沙南京广场接入停车和出发时间分别为22 : 47和22 : 53,因而设定上行先发列车在长沙南京广场停站时间为1 min。zk,x,i,zk,s,i和Dk的取值如表3所示。上下行列车在北京西高速场至广州南京广场平均旅行时间分别为10 h 42 min 和10 h 18 min,平均总停站时间分别为61 min和40 min,上下行列车的技术速度均为237 km/h;天窗开始前和确认列车开行前的安全间隔时间取5 min[1],确认列车平均技术速度为271 km/h;各阶段天窗允许最早开始时刻按图定最早开始时刻确定,最晚结束时刻按高速铁路夕发朝至列车非开行日,该阶段最早一列车图定发车(通过)时刻减天窗结束后的安全间隔时间确定。

表3 zk, x, i,zk, s, i,Dk的取值Tab.3 Value of zk, x, i, zk, s, i, and Dk
初始化边界条件T2,i,取值涵盖现有研究中定义的时间域范围,即T2,i= {[Tx,f1,Tx,f2],[Tx,d1,Tx,d2]} = {[18 : 00,0 : 00],[4 : 00,11 : 00]},初始决策集合经过493次“收缩”更新,得到当前天窗开设时长约束下的最优下行到达时间域和上行始发时间域,第一轮迭代结果如图4所示,横坐标为时刻,纵坐标为车站索引,车站索引1代表北京西站,40代表广州南站。将最优下行到达时间域和上行始发时间域作为初始条件,代入按技术速度计算的区间运行时分和各站停站时间,反推出最优下行始发时间域和上行终到时间域,最终迭代结果如图5所示。实际运行图中的时间域(其中D939次等同于下行先发列车,D930等同于上行先到列车)在输出结果的时间域范围内,输出结果如表4所示。表明模型求得的最优解是满足当前天窗开设时长要求的合理可行的始发终到时间域。
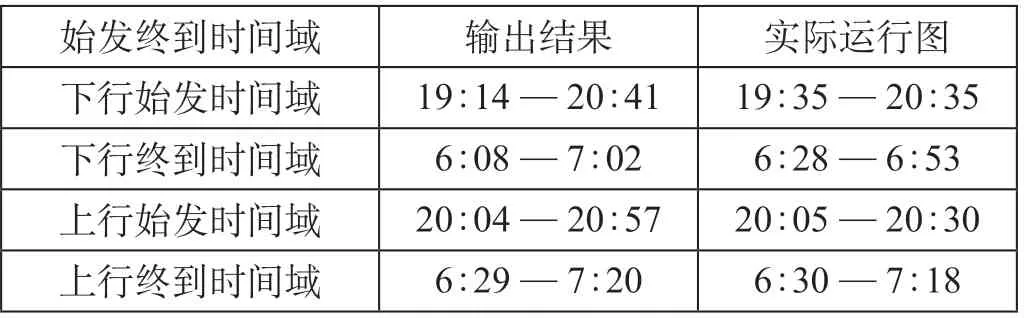
表4 输出结果Tab.4 Output results
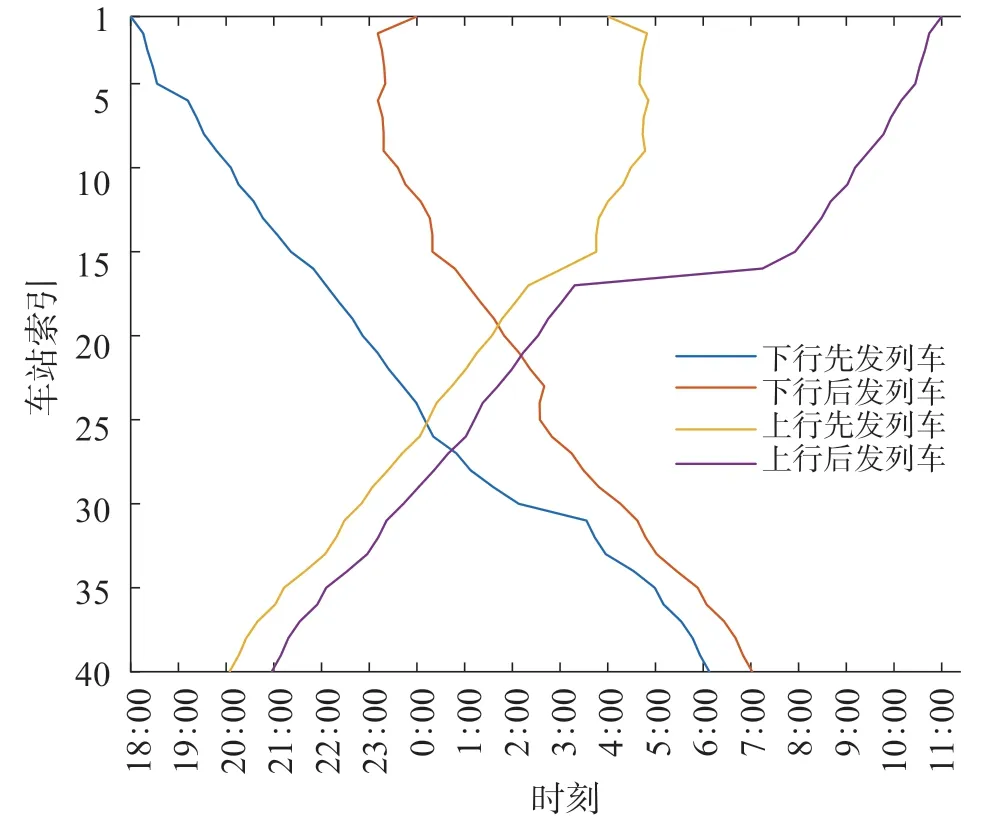
图4 第一轮迭代结果Fig.4 Results of the first iteration
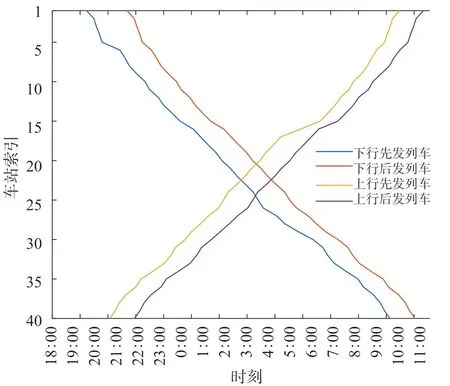
图5 最终迭代结果Fig.5 Results of final iteration
高速铁路采取分段矩形天窗的开设形式,对越靠近始发或终到的区间影响越小,算例中可以看出靠近两端的部分区间和车站可以满足连续4 h的天窗开设时间要求,中间部分区间和车站仅能满足 3 h左右的天窗开设时间要求,因而全线天窗最低开设时长要求受限于中间部分区间和车站。
通过模型,计算不同天窗开设时长要求下的始发终到时间域如图6所示。基于当前停站方案进行计算,最多能够满足全线分段矩形天窗开设时长最低为3.4 h时的要求,且上下行终到时间域长度分别为8 min和19 min,在天窗开设时长分别超过3.5 h 和3.6 h时,上行和下行列车的终到时间域长度为负值,表明计算结果已经呈现出发散的特征,即图6中的无效时间域。
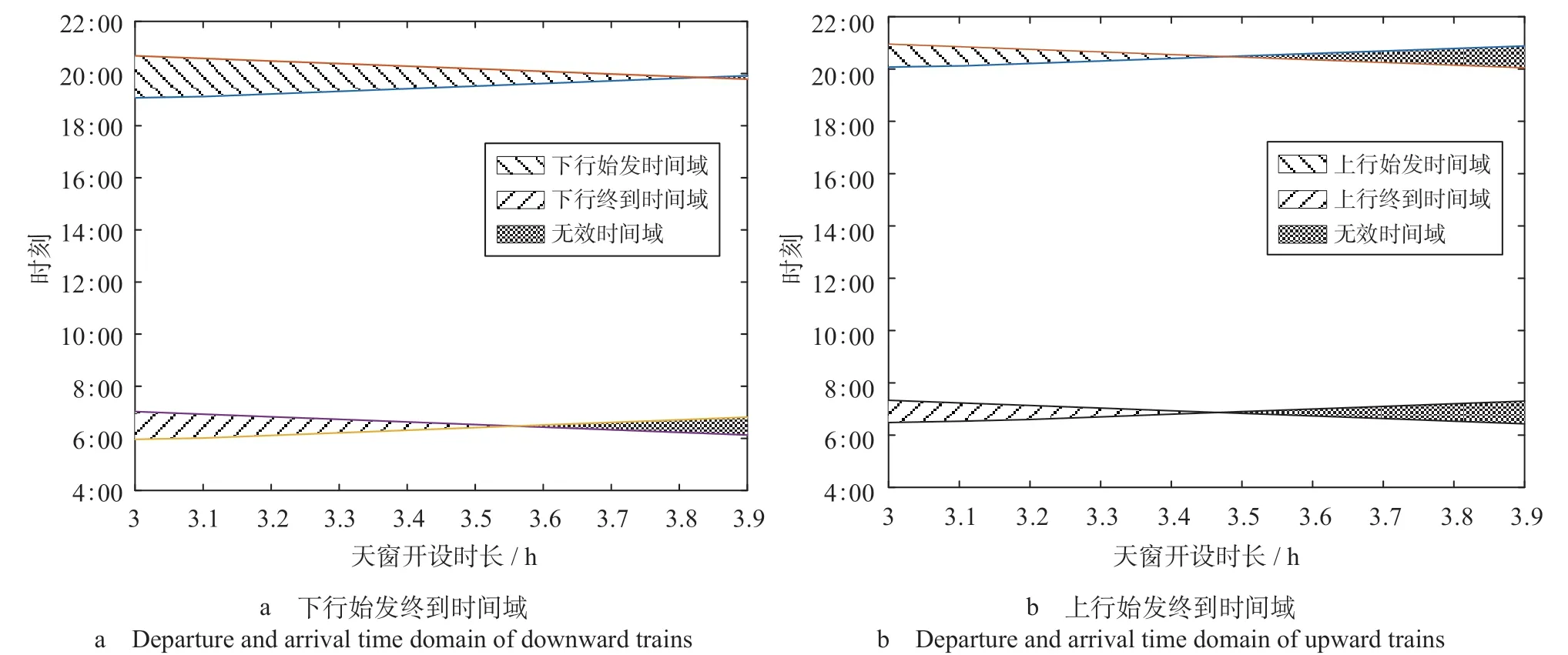
图6 不同天窗开设时长要求下的始发终到时间域Fig.6 Departure and arrival time domain for different time requirements of maintenance windows
根据计算结果,结合图3所示的模型求解过程可知,在既定的停站方案下,如果设定的天窗开设时长要求过大,算法将在步骤3和步骤4之间陷入死循环。这表示无法在分段矩形天窗的开设区域间铺画连续的运行线,导致算法无法收敛至最优解,此时需要调整停站方案或开行模式。
综上所述,输入各阶段天窗开设时长要求,在给定的停站方案下,可以通过模型和算法计算出合理的始发终到时间域。因此,该计算模型和求解算法可以有效地解决开设分段矩形天窗时的高速铁路夕发朝至列车始发终到时间域的计算问题。
4 结束语
高速铁路夕发朝至列车始发终到时间域,直接影响列车开行方案与列车运行图的编制质量。模型通过输入停站方案和各区间天窗开设时长要求,输出满足要求的列车合理始发终到时间域,可为需要开行夕发朝至列车的高速铁路列车运行图编制提供参考。计算模型是依据既有停站方案并在满足分段矩形天窗开设时长要求的约束下求解的,在实际编制列车开行方案过程中,列车的始发终到时间域还应考虑旅客的出行需求、出行时段特征等因素,这也是今后需要进一步深入研究的方向。

