鲁棒边缘粒子滤波及在目标跟踪中应用

王宗原，周卫东

(1.哈尔滨工程大学 数学科学学院，哈尔滨 150001; 2.哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001)

0 引言

滤波是基于从初始时间到当前时间的噪声测量对当前状态进行估计的一种方法。已经被广泛应用于许多领域，如目标跟踪、导航、机器人控制和信号处理[1-4]等。粒子滤波是利用加权粒子求和方法进行非线性状态空间模型状态估计的高效方法。但是高维状态如果直接用粒子滤波求解会产生维数灾难，导致粒子滤波崩溃而无法应用[3]。为了提高粒子滤波广泛的实际应用性，目前普遍关注的是从系统模型结构出发探究其是否具有条件线性子结构，从而通过状态降维方法进行状态估计。通过查阅已有文献可知，这一类模型在导航和目标跟踪领域广泛存在。目前估计最有效方法是利用Rao-Blackwellised思想设计的粒子滤波(RBPF)，或称为边缘粒子滤波[5]，它将粒子滤波与线性最优的卡尔曼滤波巧妙融合完成整体状态估计。

边缘粒子滤波由于其更优异的滤波设计方案，一经出现在导航和目标跟踪及动态贝叶斯网络中就取得成功应用，而且为适应不同系统模型及量测出现的各种新问题，近几年来研究人员对RBPF及其不同改进形式进行了广泛研究，例如，文献[6]中提出用递推期望最大化方法开发具有跳跃马尔科夫链和系统结构分解的Rao-Blackwellised粒子滤波算法；同时文献[7]利用Rao-Blackwellised准则结合RBPF平滑解决混合线性状态空间模型具有量测失序的RBPF算法性能下降问题，通过标准常加速模型的仿真结果，表明所提算法精度具有超过RBPF精度10%的性能；再有文献[8]考虑了混合线性模型线性状态方程噪声之间及状态方程噪声与量测噪声相依赖的情况，利用格莱姆-施密特解耦方法实现全部噪声协方差矩阵的对角化形式，并在常速目标跟踪模型仿真中取得优于标准RBPF精度的结果；进一步文献[9]将RBPF框架扩展到系统全部为非线性方程的模型中得到分散粒子滤波(DPF)，不同于卡尔曼滤波粒子滤波混合求解过程，DPF通过两次权值及两次重采样计算得到两次粒子混合估计结果。由以上的文献描述可见RBPF算法适用各种新出现系统问题的改进形式已被广泛探究，并且得到优于标准RBPF的结果。但据作者所知，RBPF量测噪声参数未知的改进形式还没有被涉及。

虽然模型参数未知的贝叶斯滤波已通过状态扩维法[10]或交互式多模型(IMM)法[11]进行了研究，但它们对噪声参数未知情形还无法解决。近期文献[12-13]针对噪声异常情况通过变分推断理论给出鲁棒高斯近似滤波算法，并在目标跟踪模拟中得到成功应用，但标准无迹卡尔曼滤波(UKF)或扩展卡尔曼滤波(EKF)由于样本点有限或线性化误差原因对于相同导航或目标跟踪问题精度低于边缘粒子滤波或其变形的DPF[14-15]。另外，水下运载器地形辅助导航[16]、重力梯度辅助导航等组合导航估计方法也均采用RBPF[17]，这是因为这些基于数据库图的地球物理场导航只能通过粒子表示载体全部可能位置，而且随着粒子数增加，导航精度还可能继续提高。

RBPF的另一个重要应用是在目标运动分析(TMA) 领域，也即目标跟踪，这属于通过方位测量对运动目标状态进行估计的范畴[18]。由单运动观测器收集量测形式已在无源传感领域(如声纳或雷达)具有广泛应用[19]，过去几年成为研究热点。现在关注的是用递推贝叶斯方法得到状态后验概率密度函数(PDF)。TMA的特点通过观测平台的运动对目标距离进行观测。下面将讨论贝叶斯TMA的平面跟踪问题，它将从一维方位量测集获得四维状态后验PDFs，状态包含目标位置和速度。但高机动目标跟踪通常会产生量测噪声异常问题[12-13]，影响量测噪声因素有接触实际角度、目标的距离和相对速度、信噪比、接收阵列形状、传播信道等等，这些因素很少能准确知道并且随时间推移而变化，因此工程实际中精确知道量测方差几乎是不可能的，这就造成 TMA量测噪声方差时变未知且包含异常值的特性。

注意到现有边缘粒子滤波及其各种改进形式都没对量测噪声时变的目标跟踪问题给出有效解决方案，这或许是由于如何在RBPF引入噪声参数实时估计的方法还没有被探究。为了设计具有量测方差自适应估计能力的混合系统模型的鲁棒边缘粒子滤波算法，本文将探究使用Rao-Blackwellised原理及变分推断公式对混合系统量测噪声异常问题进行状态估计，并在典型TMA的平面跟踪模型中进行仿真验证。

1 混合模型及边缘粒子滤波

1.1 目标跟踪模型

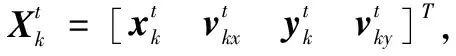
Xk+1=FkXk-Uk+1,k+Gkwk

(1)

纯角度观测模型为:

zk=atan2(xk,yk)+vk

(2)

atan2(·)表示四象限反正切函数，此处得到k时刻目标真实角度。观测噪声vk～N(0,Rk)，Rk可能是时变且未知的。

1.2 混合模型及滤波

对式(1)、(2)组成目标跟踪系统模型进行一般化引申，得到与组合导航及定位相同的如下线性非线性状态混合模型表达式：

(3)

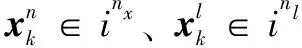
先忽略量测噪声变化的情况，RBPF的状态估计推导如下，联合状态的后验可分解为：

(4)

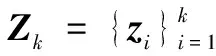
依据chapman-Kolmogorov公式，并根据高斯分布引理[12]：

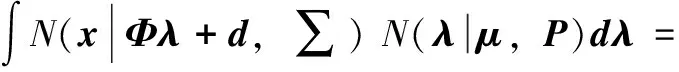
N(x|Φμ+d,ΦPΦT+∑)

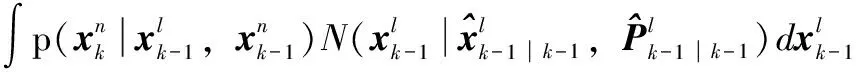
(5)

可见前一时刻线性状态后验对非线性状态预测是附加噪声，由于高斯过程噪声，非线性状态预测是如下高斯分布形式：

(6)

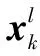
(7)

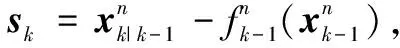
(8)

其中参数为:

(9)

(10)

(11)

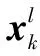
(12)

2 量测噪声鲁棒RBPF推导

下面考虑量测噪声方差未知的情形。采用将量测噪声方差视为先验分布已知随机变量，并把它应用到递推模型中，假定状态与量测噪声方差相互独立有：

p(xk,Rk|xk-1,Rk-1)=p(xk|xk-1)p(Rk|Rk-1)

(13)

其中:p(xk|xk-1)状态递推式，p(Rk|Rk-1)方差递推式。利用贝叶斯滤波公式和Rao-Blackwellised法则，可用两种方式同时求解状态和方差后验，第一种是如下分解:

(14)

(15)

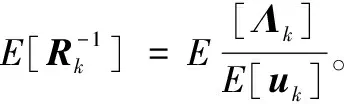
变分推断得到的后验近似分布公式:

q(Θi)∝exp{Eq(Θj≠i)[lnp(Θ|Z)]}

(16)

其中:Eq(Θj≠i)[lnp(Θ|Z)]表示条件联合PDF对异于Θi的其它参数求期望[2]。下面给出适用于所提混合模型的具体推导过程，利用贝叶斯公式，非线性状态及量测噪声参数条件联合分布表示为：

(17)

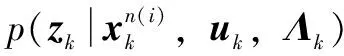
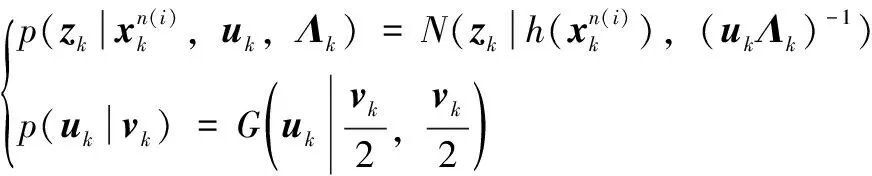
(18)

G(·|α,β)表示超参数为α,β的伽马分布，伽马分布与高斯分布一样都属于具有封闭性质共轭指数族。式(17)右端第一个表达式为高斯分布。第二个表达式噪声参数即尺度矩阵、隐变量及自由度的联合分布p(Λk,uk,vk)，设为伽马分布连乘积，又根据概率乘法公式及式(18)的第二个式子，有如下表达形式：

其中：上角标jj表示对角尺度矩阵第jj个分量,jj∈{1,2,…,m}。注意此时状态粒子权值计算式:

(19)

注意权值计算时右面量测似然是用估计的尺度矩阵与自由度的t分布表示。由于参数粒子依赖状态粒子，因此这也是参数粒子权值表达式。

为了表示噪声参数的变化情况，噪声参数预测引入波动参数ρ∈(0,1)，噪声超参数预测[2.20]表达式为:

(20)

变分推断得尺度矩阵、隐变量及自由度参数变分后验如下。

在(16)中令Θi=Λk，计算尺度矩阵变分后验PDF对数为：

(21)

可见尺度矩阵更新的超参数中包含隐变量的期望E[uk]。

在(16)中,令Θi=uk，计算隐变量uk变分后验PDFq(uk)的对数为：

(22)

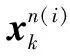
自由度变分后验计算与线性模型自由度变分后验计算相同，具体过程及结果参见文献[2]。上式超参数递推可见超参数更新过程会出现参数耦合情况，通过使用设置初始超参数值的固定点迭代方法[2]可以解决这个问题。通过概率分布的期望公式，量测噪声分布的参数期望计算为：

(23)

所提算法一步运行过程总结如下：

鲁棒边缘粒子滤波算法:

2)对每一个αk|k-1：

(1)从式(6)的建议分布提取非线性状态预测αk|k-1，用(20)预测超参数αk|k-1，βk|k-1，

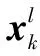
(24)

如果迭代没终止，令k=k+1, 从步骤1开始重复上述过程。

3 仿真分析比较

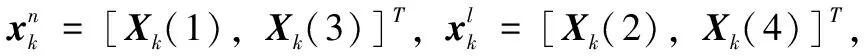
(25)

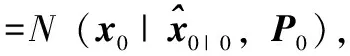
1)Rk=Rk-1+εk，εk表示量测噪声方差递推式的过程噪声被建模为高斯噪声，即：

εk～N(0,ζ2)

(26)

ζ2=0.012，单位deg2。

2) 异常时变:

(27)

实验通过一次独立实验真实位置和估计位置比较，及20次蒙特卡洛仿真均方根误差来衡量不同算法的性能。均方根误差(RMSE) 定义式为：

(28)

对于所给量测噪声方差设置，此时标准RBPF算法运行经常有失效情况发生，具体为RBPF算法在迭代几个时间步后算法失效，原因是粒子滤波运行崩溃，从而导致整个滤波失效。而所提量测鲁棒边缘粒子滤波算法则始终在每次蒙特卡洛仿真时正常稳健运行。

下面将RBPF能正常运行情况下x-y面轨迹图及东向与北向RMSE图进行比较。图1～2为第一种噪声情况下与标准RBPF算法比较的RMSE图及轨迹图。

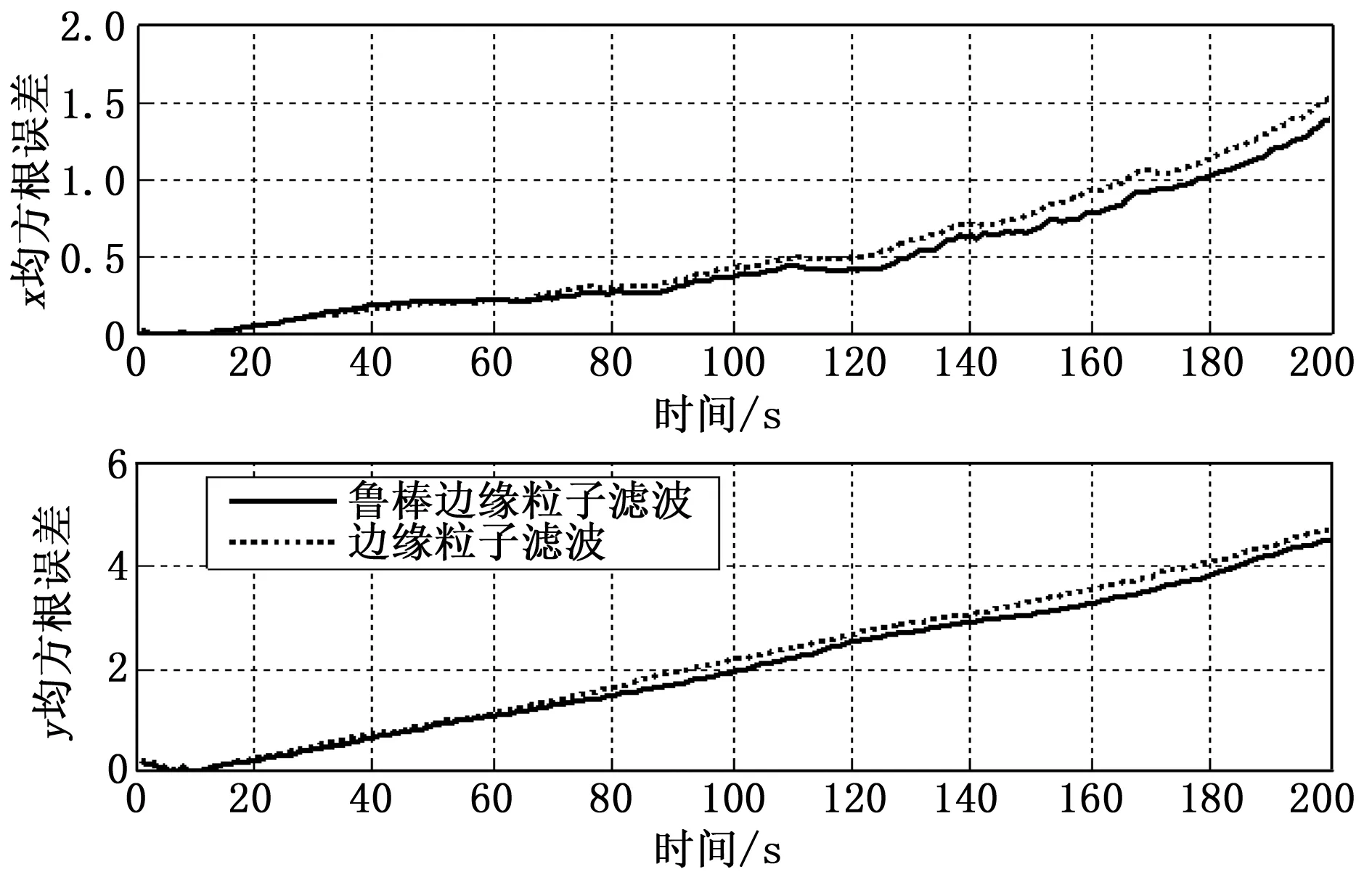
图1 噪声1下所提算法和RBPF算法估计轨迹RMSE比较图

图2 噪声1下真实轨迹与RBPF算法和所提算法轨迹比较

表1 噪声1下所提算法和RBPF算法目标跟踪性能比较

从位置的具体数值上可以看到两种算法对问题描述的目标跟踪问题都有较高的估计精度，即使所选择的粒子数仅为100。而所提算法在X、Y方向的RMSE精度上要略高于所比较的RBPF，说明在此种量测噪声方差缓慢变化的情况下，所提具有方差自适应鲁棒边缘滤波算法更具有状态估计优势。

图3～4为第二种噪声情况下两种算法的东向与北向RMSE及轨迹比较图。从图3～4可见，在x轴方向所提算法状态估计精度略高于RBPF算法的精度；对于y轴方向精度可见除个别时间点外，所提算法的状态估计精度对已有RBPF算法有较大提高；相比于RBPF位置估计，所提算法位置估计更靠近真实位置。具体数值如表2所示。

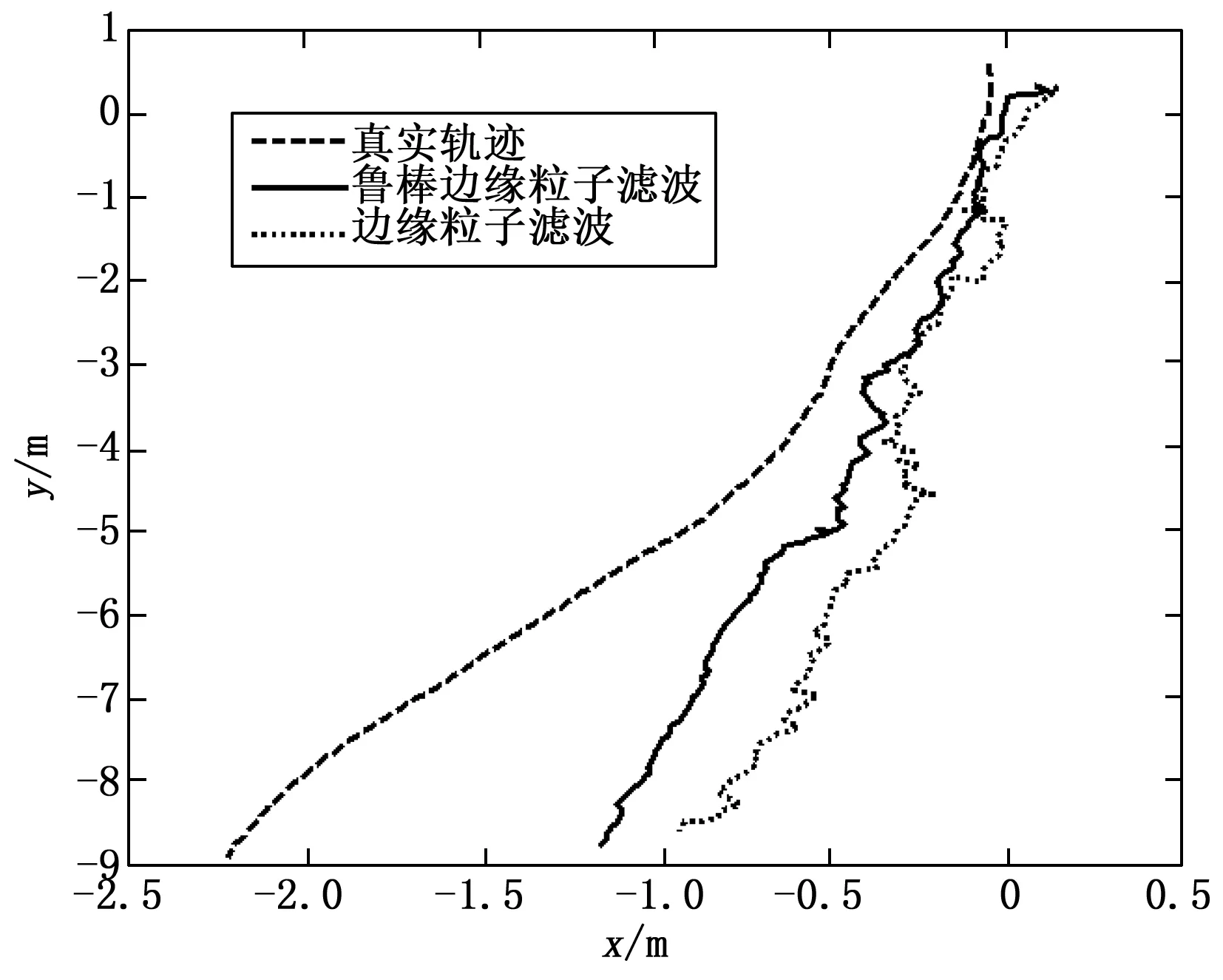
图4 噪声2下真实轨迹与RBPF算法和所提算法估计轨迹比较

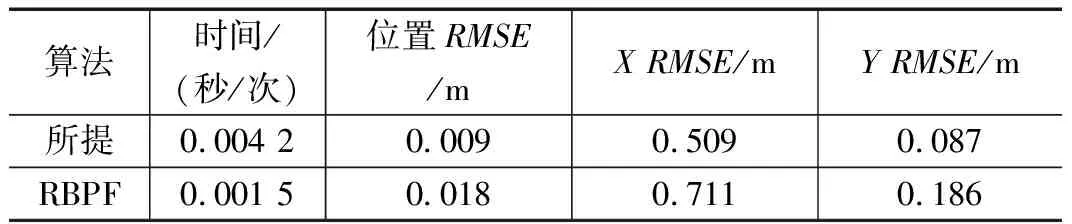
表2 噪声2下所提算法和RBPF在目标跟踪性能比较

第二种噪声情况下，即使RBPF算法能够正常运行，所提算法的精度更高，相比于第一种噪声结果优势更加明显，说明第二种噪声情况下所提算法更具有适用性。

当然，如果噪声方差是恒定不变且事先精确已知的情况下，已有RBPF算法精度略高于所提算法，因为所提算法的方差是用算法实时估计的方差计算，而RBPF算法是用精确已知的方差，这也解释了为什么第二种噪声情况某小段时间内RBPF精度高于所提算法。

另外虽然所提算法在CV模型中仿真验证，可以验证对常加速度CA的目标跟踪问题也同样具有优异性能。另外所提算法单次仿真时间近似为RBPF算法单次运行时间的2.5倍。

4 结束语

由于边缘粒子滤波在导航和目标跟踪中的不可替代性，本文对现有边缘粒子滤波无法解决量测噪声方差未知的问题进行研究，通过将学生t分布加入混合模型，利用Rao-Blackwellised思想分别实现状态条件降维及参数与状态的同时估计，由此开发出一种鲁棒边缘粒子滤波。文中推导了噪声参数及含有噪声参数状态的递推计算公式，并把所提算法在典型目标跟踪模型中及设置的两种不同量测噪声下进行仿真分析，结果表明这两种情况下都具有更优越的估计性能。