基于电路控制的梯度折射率曲面声学透镜研究

陈 峰,廉 盟,曹 暾,

(1.大连理工大学 生物医学工程学院，辽宁 大连 116024;2.大连理工大学 光电工程与仪器科学学院，辽宁 大连 116024)

0 引言

声学超材料可以实现自然界中不常见的材料声学性能，为新型声学器件研发提供了可能，如隐身斗篷[1-3]，波前转换器[4-5]，声学聚焦透镜[6-9]等。其中，声学梯度折射率(GRIN,gradient index)透镜[10-14]是一种特殊的声学超材料，因其折射率在介质中的空间分布状态不断变化，可改变声束的传播路径，具有衍射极限以下超声成像等应用潜力，为医疗器械、秘密通信、声学检测等领域提供了无限可能。国内外相关研究机构已经利用声子晶体与声学超材料设计多种类型的声学GRIN透镜，通过改变单元的结构参数, 实现不同的梯度折射率的声学效果。如2016年袁保国[15]等人提出了一种二维声学麦克斯韦鱼眼透镜，该透镜采用空间螺旋形声学超材料，成功地将声波从其表面的点源辐射到透镜直径相反的一侧。2020年J. Hyun等人[16]提出了一种由填充分数不同的圆柱体组成的对称GRIN声子晶体结构，以调整空间声折射率，从而使声波向目标中心区域的任何方向聚焦。

尽管声学GRIN透镜具有新型而奇异的特性，但由于其梯度折射率的实现全部依赖于几何阵列结构的渐变，制造复杂、成本较高。相比于以上基于声子晶体和卷曲空间的结构型变折射率材料来实现声学透镜的方式，近年来，在电磁波，水面波，弹性波等领域已经提出了采用不同常规材料组成非均匀介质的GRIN透镜装置。2015年王振宇等人[17]将通过逐渐改变水深来控制水面波传播，实现线性水面波所需的梯度折射率，以控制水波的弯曲、定向发射和聚焦。2016年Mitchell-Thomas等人[18]利用在金箔表面不同厚度的有机玻璃在GHz波段制作了表面电磁波隐身斗篷。通过合适的折射率曲面修正了由于曲率引起的面波阵面形状的畸变。然而上述GRIN透镜模型只能实现一种特殊的波导现象，不具备功能调谐性。如果一种透镜能够在人为操纵下实现两种及以上的声学现象，将为复杂的声波成像器件提供新思路。

本文提出了一种基于折射率可调谐材料的声学透镜，采用有限元数值方法，基于多层变折射率爱因斯坦环形的RineHart曲面壳体结构[19]，建立RineHart曲面折射率模型，调控外部电路控制改变材料折射率的梯度分布[20]状态，实现声波传播路径的操控，形成功能可切换的波形转换声学器件。

1 三维声学GRIN透镜结构设计

变换声学理论提出一种二维平面声学透镜，通过改变二维平面空间声学折射率分布来控制声波的传播路径。受爱因斯坦环的启发，本文采用不同声折射率层介质弯曲声束代替引力场环弯曲光束的方式，构造三维曲率空间声学透镜，实现声波的重汇聚。三维曲面声学透镜的结构如图1(a)所示，由一系列直径不同的圆环层沿z轴叠加组成，圆环材料声折射率沿z向发生梯度变化，实现波形操控。

图1 Rinehart曲面声学透镜几何和数学模型

三维声学透镜的梯度折射率N(ρ)分布如图1(b)所示，其中ρ是截面圆环的半径，球形表面上任意临近的A、B两点之间距离dL，根据微分三角形可表示为：

dL2=ds2+ρ2dθ2

(1)

式中，s是z向顶点到沿母线C任意点S对应的弧长，θ是S点对应截面圆环的中心角。将dL乘以折射率n，得到A、B两点之间的声程dφ：

dφ2=n2(ds2+ρ2dθ2)

(2)

以自定义曲面坐标系代替柱面坐标系，将便于曲面上声程的计算，其中曲面坐标系的3个自变量为s，ρ和θ。如果以曲面坐标系的ρ和θ作为自变量，公式(2)可写为:

dφ2=N(ρ)2(s'(ρ)2dρ2+ρ2dθ2)

(3)

如果以曲面坐标系的s和θ作为自变量，公式(2)可写为:

dφ2=n(s)2(ds2+ρ(s)2dθ2)

(4)

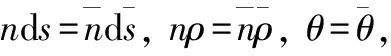
(5)

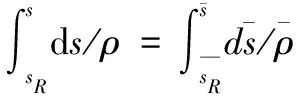
(6)

式中，R为RineHart曲面底部边界(z=0)上的点，sR为z向顶点到R点对应的弧长。

Nρ=n(r)r

(7)

(8)

N(s)=n(r)[f(s) ]f(s)/ρ(s)

(9)

(10)

将公式(10)代入式(9)中，可以得到三维曲面透镜的折射率分布为

N(ρ)=n(r)[F(ρ) ]F(ρ)/ρ

(11)

本文中三维曲面透镜采用了RineHart曲面，对应的s与ρ关系为s=0.5ρ+0.5sin-1ρ。将s代入公式(10)，则曲面的折射率分布是与ρ和n(r)有关的变量，n(r)是二维平面透镜各种声学现象对应的梯度折射率分布，如表1所示。ρ是归一化变量，相当于r/R。因此，根据二维透镜的梯度折射率分布状态即可以设计出具有相同功能的三维声学透镜折射率分布状态。

表1 平面声学透镜折射率分布公式

2 声学GRIN透镜性能调控方法

根据上文曲面声学透镜的理论设计，证明了不同声学器件效果可以通过改变曲面壳体不同层段的折射率实现，而折射率又可以通过介质间的声速比值表示。因此本文将关注于如何实现制备材料声速可调控的曲面声学透镜。琼脂糖水凝胶材料是一种温敏材料，当温度发生变化时琼脂糖水凝胶中的结合水和自由水会相互转换，材料特性会变化，实现了声速可控。通过在低温区域对含水量为65%的琼脂糖水凝胶的声速进行测试，获得对应的声速与温度的变化关系。测试方法如下：预先将含水量为65%的温敏水凝胶用液氮进行低温冷却至-30 ℃；然后，在温敏水凝胶材料侧壁粘贴温度传感器；最后，停止液氮喷射，在20 ℃室温环境下，实时测量温敏水凝胶材料升温过程中的声速，声速曲线如图2所示，为了获得合适的仿真数据，采用最小二乘法对超声声速曲线进行了拟合，拟合公式如下：

图2 低温区域水凝胶的声速变化曲线

v=0.693 7t2-12.782t+2 054.1

(12)

根据上文的平面透镜折射率分布和公式(11)、(12)，将不同声学功能对应的梯度声速和温度分布通过电路装置调控在曲面声学透镜上实现对应的声学器件。考虑到琼脂糖水凝胶的低温梯度调控的可实现性，需要先将制备好的曲面声学透镜统一降温处理，再按梯度声速分布对不同位置的片段升温，形成低温区域的温度梯度分布。本文选取了室温20 ℃条件下温敏水凝胶的声速作为曲面声学透镜的梯度分布下界值vb，其数值为2 000 m/s，对应折射率分布上界值nb为0.74。

电路温控方法如图3所示，首先，将曲面声学透镜放置在内置温度传感器的可拆卸封闭腔内中，PLC控制器通过开关电磁阀来控制液氮管道中液氮的流通。预设环境温度为-35 ℃，腔内温度传感器将温度转换为电信号发送至上位机对PLC控制器进行反馈[22]。

图3 曲面声学透镜的调控测试图

然后，为控制曲面声学透镜的温度分布，本文在不同温敏水凝胶片段内表面上粘贴了导电电极片和温度传感器，利用热电阻电路对声学透镜材料进行加热。通过电路控制器改变恒流源的电流值[23]，使热电阻电路末端的导电电极片独立加热相连的水凝胶片段。最后，我们根据测试所得的低温区域水凝胶材料声速变化规律，在软件系统设置曲面声学透镜需要的温度参数。PLC控制器会预先设定好环境参数，电路控制器会将温度输入转换为电流输出，使曲面声学透镜在电路系统控制下实现低温区域的声速梯度分布。

3 仿真结果

本文采用有限元多物理场耦合软件COMSOL Multiphysics模拟三维曲面透镜的声学特性。透镜几何参数分别为：衬底采用长方体结构，长为400 mm，宽为300 mm，高度为4 mm。底板上方有近似于椭球形的壳体，半径为100 mm，高度为63.2 mm，层厚为4 mm。仿真主要实现3个声学现象，即隐身斗篷、吕内堡透镜、鱼眼透镜。

3.1 隐身斗篷

根据二维隐身斗篷声学器件的折射率分布以及公式(11)，计算得到三维声学透镜折射率分布公式为:

(13)

计算得出的N(ρ)离散分布值对应的梯度声速分布如图4(a)所示。图4(b)显示了平面波在70 kHz时隐形斗篷的性能。由于该折射率梯度分布，声束在曲面透镜上两点之间传播的声程与对应平面透镜上投影点之间的声程相同，可以发现经过曲面透镜左右的平面波传播方向、振动相位均不发生改变，声波在传播过程中因材料特性与传播方式会有些许能量衰减。经仿真分析波长越大，衰减程度越低。即以俯视视角看三维曲面透镜上的声波传播路径，与平面波在二维平面上的传播效果保持一致，证明了在此梯度折射率分布下曲面透镜可以将物体隐藏在凹凸处而不被发现。

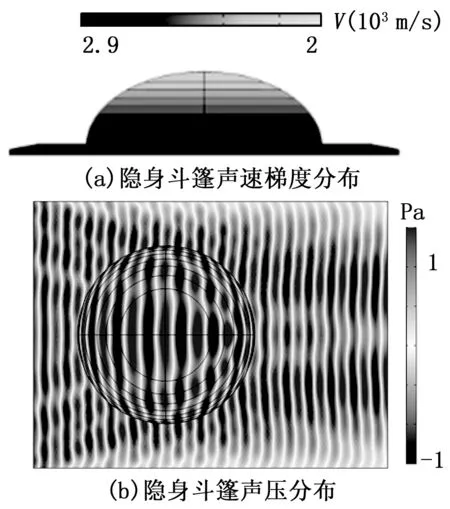
图4 70 kHz隐身斗篷的仿真结果

3.2 吕内堡透镜

由于设计的RinHart曲面的特殊性，根据二维吕内堡声学透镜的折射率分布以及公式(11)，计算得到折射率分布N(ρ)恰好为常数，因此本文三维透镜折射率分布N(ρ)统一设置为nb，得出对应的梯度声速分布如图5(a)所示。图5(b)显示了平面波在70 kHz转换为柱面波的现象，RineHart曲面结合材料折射率会对平面波的传播方向与振动相位进行调控，经过曲面透镜后的声波能量聚焦在曲面边界的一点上，以柱面波的方式向右侧传播。证明了在此梯度折射率分布下曲面透镜可以实现平面波与柱面波的波前变换，且保证振动声压近乎不变。同样的，如果以柱面波源在此曲面透镜上进行传播，也会得到相应的平面波。

图5 70kHz吕内堡透镜的仿真结果

3.3 鱼眼透镜

针对柱面波特性，本文根据鱼眼功能二维声学透镜的折射率分布以及公式(11)，计算得到三维鱼眼透镜折射率分布公式为:

(14)

计算得出的N(ρ)离散分布值对应的梯度声速分布如图6(a)所示。图6(b)显示了柱面波在70 kHz时的对称鱼眼现象。由于该折射率梯度分布，RineHart曲面结合材料折射率分布会对柱面波的传播方向与振动相位进行调控，使经过曲面透镜后的声波波前汇聚成点，在曲面透镜底部右侧边界产生一个对应左侧点声源的伪点声源，并以此在透镜右侧以柱面波方式传播，在传播过程中因聚焦伪点声源导致曲面透镜左右两侧振动声压一致，证明了在此梯度折射率分布下曲面透镜可以实现两侧对称的鱼眼幻像。

图6 70 kHz鱼眼透镜的仿真结果

4 透镜效果的影响因素分析

为了验证RineHart曲面透镜梯度参数分布的离散化程度对上述曲面透镜功能的影响，本文以鱼眼透镜为例探究了声速梯度离散水平对该现象的影响，图7(a)、(b)、(c)左侧图分别为6、9、12层离散化鱼眼透镜的梯度声速分布，右侧图则分别说明了入射声波(f=70 kHz时)在被分为6、9、12层的曲面透镜模型上的声波传播效果。可以观察到，当声速梯度以图6(a)左侧图分布时，6层结构的离散水平也可以实现鱼眼效果，但曲面透镜上两点之间的声程与由N(ρ)计算得到的声程存在一定误差，柱面波波前畸变严重。反之层数越多波形畸变越小，柱面波波前越趋近于平滑，呈现的鱼眼透镜效果也越好。特别当层数达到9层以上时，效果改善程度较不明显。因此，所以综合考虑9层梯度折射率声学曲面透镜是一个较合理的选择。

图7 梯度声速分布离散化对曲面透镜的影响

此外，本文还探讨了不同频率的声波在RineHart曲面透镜上的传播效果，计算了透镜的宽带。同样以鱼眼透镜为例，本文探究了不同频率的超声对鱼眼透镜的影响，图8(a)、(b)、(c)说明了入射声波在9层模型上频率分别为35 kHz、70 kHz和105 kHz的声束传播轨迹。当入射声波的频率低于23 kHz时，声波波长不再远小于空间特征尺寸，无法明显观测声学透镜的呈现效果，估算频率宽带的下界为23 kHz。当入射声波的频率高于115 kHz时，柱面波的波前也不再平滑，声能量损失过多，呈现效果低于预期。依照此思路对透镜适用的频率宽带上界进行了估计，约为118 kHz左右，验证了其频率宽带特性。如果将三维梯度折射率声学透镜应用于其他频率声波操控中，可以通过改变透镜模型几何尺度或者改变梯度折射率分布的上下界范围来实现。

图8 Rinehart曲面透镜在不同频率下的仿真结果

5 结束语

综上所述，本文提出了一种基于电路控制的三维Rinehart曲面声学透镜。通过电路控制系统与液氮控制器的温度控制技术实现曲面声学透镜上折射率与声速的梯度分布呈不同规律时，可控制透镜具有不同的声学功能效果，为声学路径操控提供了新的方法，仿真实现了隐身斗篷，吕内堡透镜，鱼眼透镜等功能。此方法不同于以往的基于声子晶体或声学超材料的传统梯度折射率透镜，声学透镜结构简单、制造难度低，且具有快速可调换的多功能特性，为多功能声学透镜的设计制造提供了新思路。