基于声光阵列的炸高测量技术研究

王 永，宋玉贵

(西安工业大学 光电工程学院，西安 710021)

0 引言

炸高测量是现代武器效能评估的重要内容，如末敏弹、枪榴弹和空爆弹的炸高，就是衡量该类武器性能的重要指标之一。国内采用的炸高测量方法主要有CCD交汇测量法[1]、卫星雷达测量法[2]和大视场电视经纬仪测量法[3-4]，此类测量方法虽然测试精度较高，但是测量原理非常复杂，成本高昂，只局限于特定的的武器系统，而且测量时受气象和电子干扰的影响较严重。利用测量爆炸声源到声传感器的到达时间差[5-8]( TDOA, time difference of arrival)来确定炸点的位置，不仅可以快速确定炸点位置，而且极大地降低了成本、提高了定位精度，同时还具有隐蔽性。研究基于无源被动式探测原理的空中炸点定位算法具有较好的理论意义以及很高的实际应用价值。张晓光[9]等人提出一种基于四元十字麦克风阵声源定位系统,该系统的定位坐标偏差在7%之内，应用在炸高测量上无法满足要求。王洋[10]等人提出的3个五元十字阵列的弹丸落点定位满足靶场对弹丸落点的全域定位精度要求，其结构较复杂，布局比较繁琐，导致对测量距离要求比较高，并且只是在理想环境下进行的仿真实验。

目前，应用于靶场炸高测量的的探测方式主要分为有源主动式定位和无源被动式定位两种[11-12]；其中，有源式主动式定位技术是通过发射高功率的信号波来实现定位，定位精度较差。而无源被动式定位系统是通过采集目标本身发射的声光等信号来实现定位，不需要跟踪武器弹药的飞行轨迹，也不受被测目标特性以及电子干扰等影响，定位精度高。当然，基于无源被动式定位的声学测量技术也有需要改进的地方。例如，使用单基阵麦克风阵列无法精确测量炸点高度，采用多基阵测量炸点高度时，结构比较复杂，布阵繁琐费时，并且需要进行数据融合，增加了计算量。

针对上述问题，本文提出一种基于立体六元声光阵列的新型炸高测量系统，引入改进的广义二次互相关时延估计算法可以在低信噪比下准确获取TDOA，并根据列出的数学模型计算声源的高度，实验结果表明，该设计可以实现单基阵测量炸高，并有效提高了时延估计的精度与抗噪性能。

1 立体六元声光阵列定位原理

声源定位系统根据测量目标的不同要求采用不同的定位模型。当声源信号在二维平面上时，只需确定目标在二维空间上的信息，当声源信号在三维空间上时，就需要使用比较复杂的立体定位模型来确定声源的位置[13]。由数学原理可知，若要在三维空间里确定一个点，至少需要3个距离差，4个观测点。

本文主要研究远场三维空间中的炸高测量，提出了一种立体六元声光阵列测量结构，如图1所示，该结构由一个声光组合传感器(ML)和5个声传感器(Mic1-Mic5)组成，其中，光传感器位于坐标原点处，声传感器分别位于坐标轴上，且距离原点距离为d。设待测炸点S的坐标为(x,y,z)，到声光组合传感器件ML的距离为r，到声传感器Mic1-Mic5的距离分别记为r1、r2、r3、r4、r5。

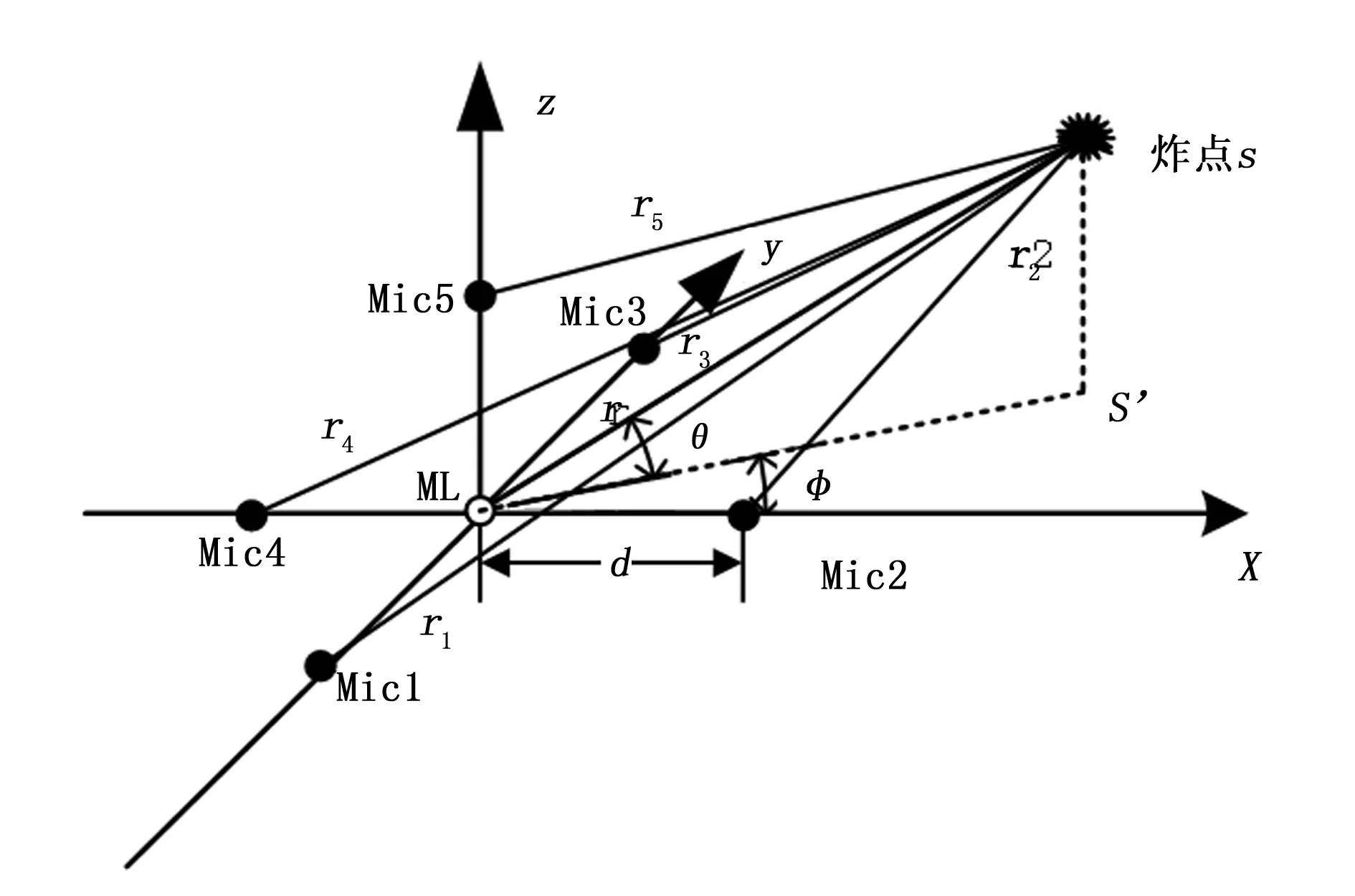
图1 立体六元声光阵列模型

根据声波到达各个声传感器的时延差可以列出以下方程组：

(1)

ri-r1=τ1iC,(i=2,3,4,5)

(2)

声波在空气中传播时，声速C与环境温度T、压强P的关系为:

(3)

式中，τ1i表示声源信号到Mic1和Mici之间的时延差，Pw为相对湿度与对应温度饱和蒸汽压的乘积。

联立式(1)、(2)可得：

(4)

(5)

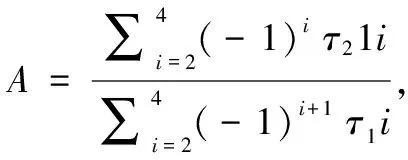
(6)

炸点位置的俯仰角θ为：

(7)

炸点到光传感器的距离r为：

(8)

最终计算的炸点高度h为：

h=r· sinθ+b0=

(9)

式中，△t为声光信号到达基阵的时延值，V表示光在空气中传播的速度，b0为基阵原点到地面的距离。

2 声光阵列测量炸高误差分析

由第一节的数学模型可知，炸点位于基阵中心的的俯仰角θ与时延估计值τ1i有关，通过测量爆炸火光与爆炸声音到达测量基阵的时延差△t以及空气中的声速C便可以算出炸点距离r。最终通过公式(9)可以算出炸点高度h。因此，影响声光阵列炸高测量精度的主要因素为时延τ1i、爆炸声光信号到达基阵的时延估计值△t和空气中的声速C。

使用Matlab软件[14]仿真炸点位于阵元中心的俯仰角θ受阵元间距d以及时延τ1i的影响程度。仿真过程中取测试环境中的声速为340 m/s，炸点分布范围为200 m *200 m *100 m；由于信号采集卡的分辨率固定，为了保证时延估计的有效性，阵元间距不宜过小，但若阵元间距过大，会对系统的便捷性和可实现性产生一定的影响，故仿真时选取的阵元间距在0.6～3 m范围内，引入时延估计误差，采用蒙特卡洛[15]方式，进行300次重复试验，最终获得在不同阵元间距下，时延估计误差导致的炸点俯仰角误差，结果如图2所示。

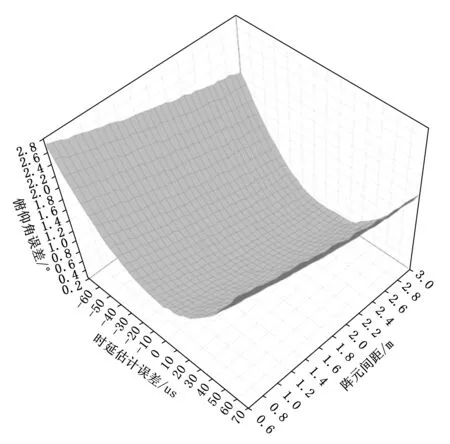
图2 不同阵元间距下时延估计误差导致的俯仰角误差

采用上述同样的方法进行150次仿真试验，图3是炸点的平面位置分别在(10 m,10 m)、(50 m,50 m)和(100 m,100 m)处的炸点距离相对误差与炸点高度的关系。

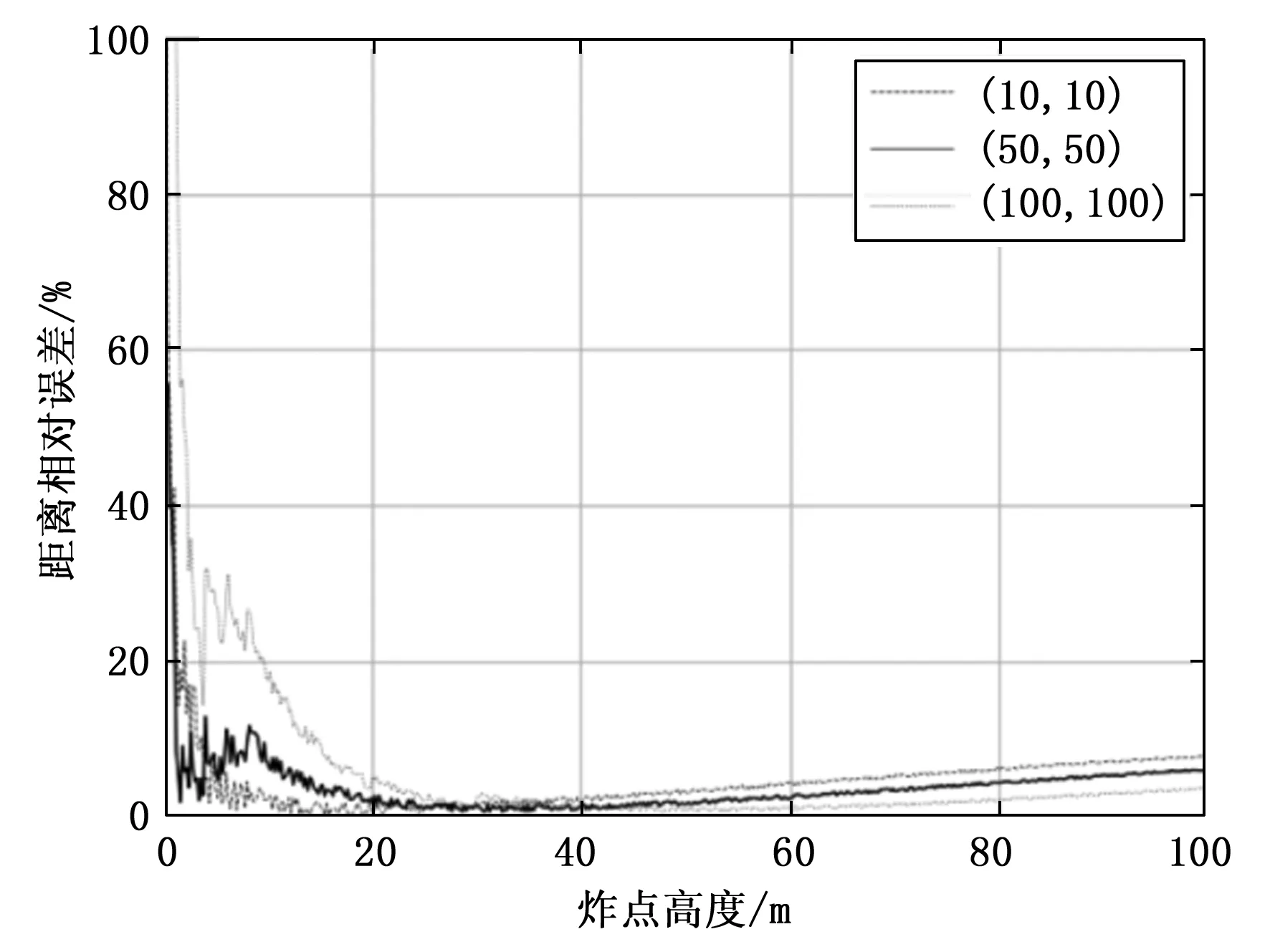
图3 炸点距离相对误差与目标距离之间的关系

由图3可知，炸点平面位置为(5 m,5 m)、(50 m,50 m)和(100 m,100 m)时，离地距离较近的区域距离误差较大，误差波动较大，随着炸点高度的增加，距离误差逐渐减小，在高度为30 m时误差最小，误差波动较稳定；不同平面位置的炸点在25～60 m高度处的距离误差小于4%，误差相对较小。

图4为炸点位置到测量基阵原点的距离r受声速变化及爆炸声光信号到达基阵的时延估计值Δt误差的影响图。

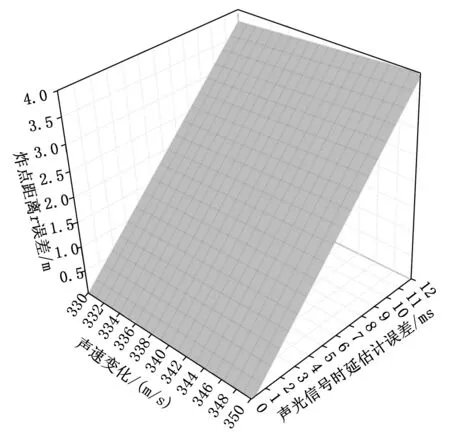
图4 炸点距离误差与声速变化和声光信号时延估计误差的关系

由图4得，炸点距离误差与声速变化和声光信号时延估计误差呈正比，声速变化为20 m/s时导致得炸点距离误差不大于0.5 m,对炸点距离的影响较小；声光信号时延估计误差为12 ms时导致的炸点距离误差范围为3.8 m附近，对炸点距离影响较大。因此测量炸点距离时应该尽可能减小声光信号时延估计误差。

综上分析，本文所提测试方法适用于高度范围为25～50 m的炸高测量，最佳测量声信号延估计误差绝对值不高于20 μs，声光信号到达基阵时延估计误差不高于4 ms；为了确保声光阵列炸高测量的精确度，阵元间距不应小于2 m。时延估计精度取决于时延估计算法的性能，声光信号到达基阵时延估计误差的精度取决于硬件电路(本文暂不讨论)。

3 时延估计算法

在声信号处理放大电路性能完全一样的情况下，时延估计算法性能决定了时延估计的准确率。在众多的时延估计算法中，通过广义互相关算法[16-19](GCC, generalized cross correlation)分析的时延估计原理最简单，运算量小、易于实现，实际应用最为广泛。文献[20]提出相位变换加权广义互相关算法(GCC-PHAT)对于宽带准周期的语音信号，相关峰尖锐，时延估计效果最好，但随着信噪比的下降，估计性能下降很快。除此之外，在对两路信号进行广义互相关计算时应用的快速傅里叶变换(FFT,fast fourier transform)存在栅栏效应, 降低了频谱的精度，得到的时延值总是采样间隔的整数倍，时延估计精度为TS/2[21]，反应不出精确的信号的频谱特性。

采用MCZT(MCZT,modified chirp z transform)算法代替FFT计算音频信号细化的频谱，不仅可以提高频谱分辨率，而且可以降低干扰噪声的影响，通过计算两信号的自功率谱、互功率谱以及二次互功率谱，采用相关峰精确插值[22-24]( FICP， fine interpolation of correlation peak)对二次互功率谱进行补零来提高频域采样率，提高时域相关函数的分辨率，接着对二次互相关函数做归一化运算和指数运算，使得峰值突出，易于读取峰值，经过峰值检测最终得到时延估计值。算法流程如图5所示。

高分方案数代表来自外部评价指标的设计师产出质量(本实验采用外部专家组评价每一款方案)，被引用次数则代表设计师的作品在团队内部的认可度。内外两个指标结合起来可以作为设计师产出质量的一个较全面的表征。

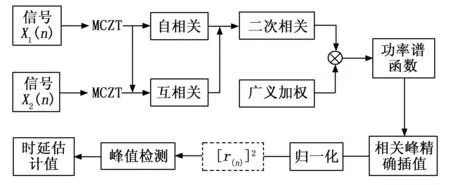
图5 改进的广义二次互相关算法流程

图5中虚框内的公式可表示为：

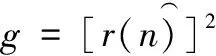
(10)

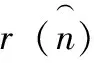
假设两个声传感器接收到的声信号的时域序列分别为x1(n)和x2(n)，用MCZT变换分别计算两路信号的细化频谱X1(k)和X2(k),接着计算其自功率谱R11(k)和互功率谱R12(k)。

(11)

式中，k=0，1，…，N-1。

自功率谱R11(k)为：

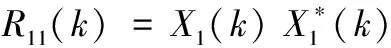
(12)

互功率谱R12(k)为：

R12(k)=X1(k)X*2(k)

(13)

二次相关处理可以进一步减少噪声的影响，提高信噪比，其互谱为：

R(k)=φ12(k)R11(k)R*12(k)

(14)

其中：φ12(k)是加权函数，该算法采用的加权函数为改进的ECKART加权函数，表达式为：

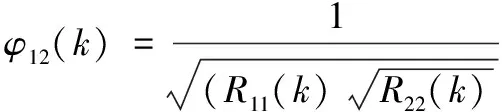
(15)

由于使用ECKART加权函数时需要预先知道噪声的自功率谱，这在实际中很难获得，因此本文对ECKART加权函数进行了改进，由谱的共轭对称性可得N1点的完整互谱R1(k):

(16)

为提高时域相关函数分辨率，对频域互谱R1(k)补零加长，周期延拓成N2点的序列，其分辨率提高N2/N1倍。

(17)

式中，N为初始信号序列长度，N1和N2需满足N2≥N1≥2N-1,n=0,1,…,N2-1。

对R2(k)进行IMCZT逆变换得到二次互相关函数r(n):

(18)

对二次互相关函数做归一化处理得：

(19)

式中，ε是为了避免除数为0时所使用的微小正数，取值为0.000 001。

4 改进后的算法仿真分析

为了验证改进算法的时延估计性能，利用MATLAB给两段时延估计值为1 ms声源信号添加不同信噪比(SNR=-15 dB、-5 dB、0 dB)的随机噪声来进行模拟噪声实验，分别使用广义二次互相关算法和改进的广义二次互相关算法分别对两路声源信号做互相关求其时延估计值，通过相关结果的峰值来判断时延估计的精确度，主峰越凸显,其时延估计性能越好。图6为时延估计值为1 ms的两路声源信号。互相关函数结果如图7～9所示。

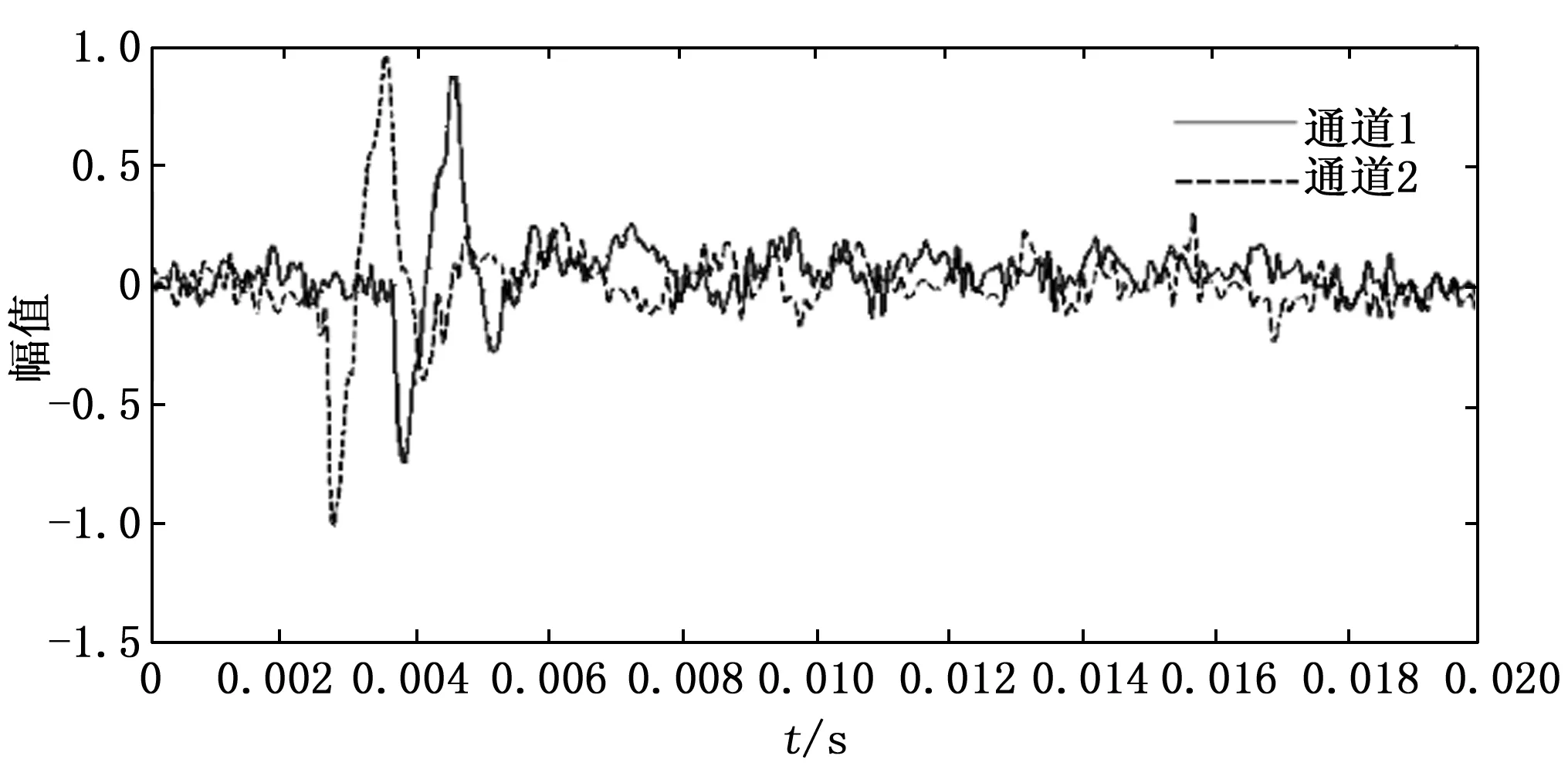
图6 时延估计值为1 ms的两路声源信号

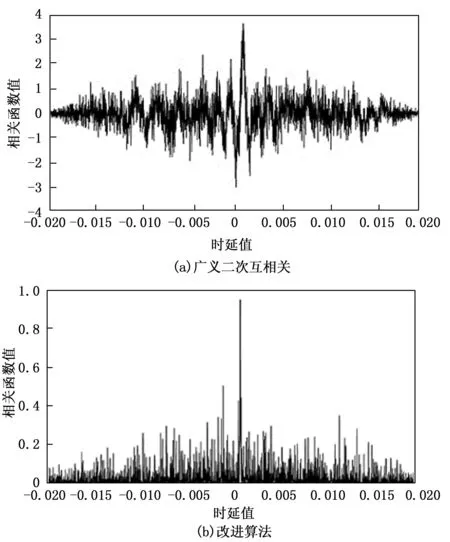
图7 SNR=-15 dB时两种算法的时延估计结果

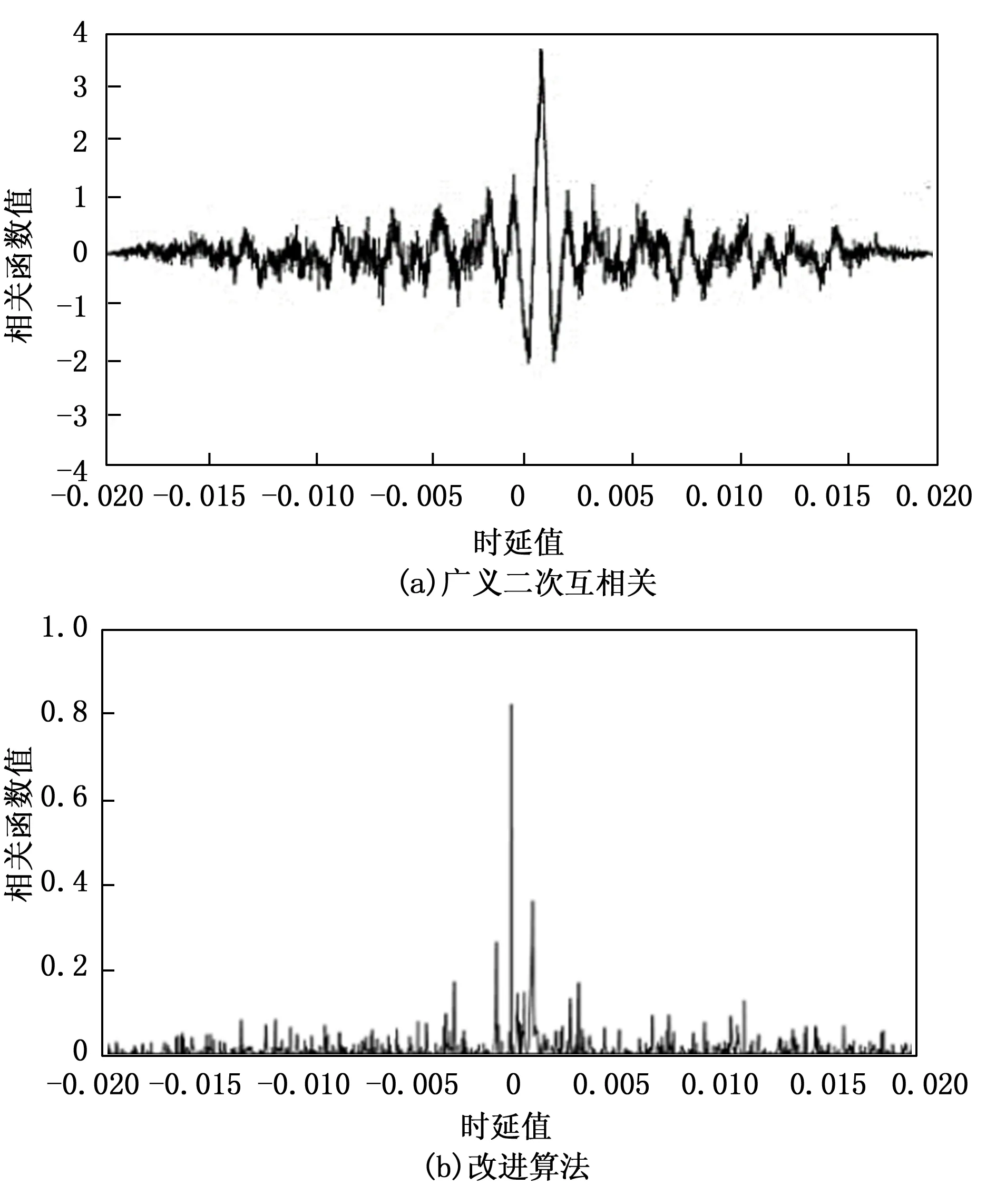
图8 SNR=-5 dB时两种算法的时延估计结果

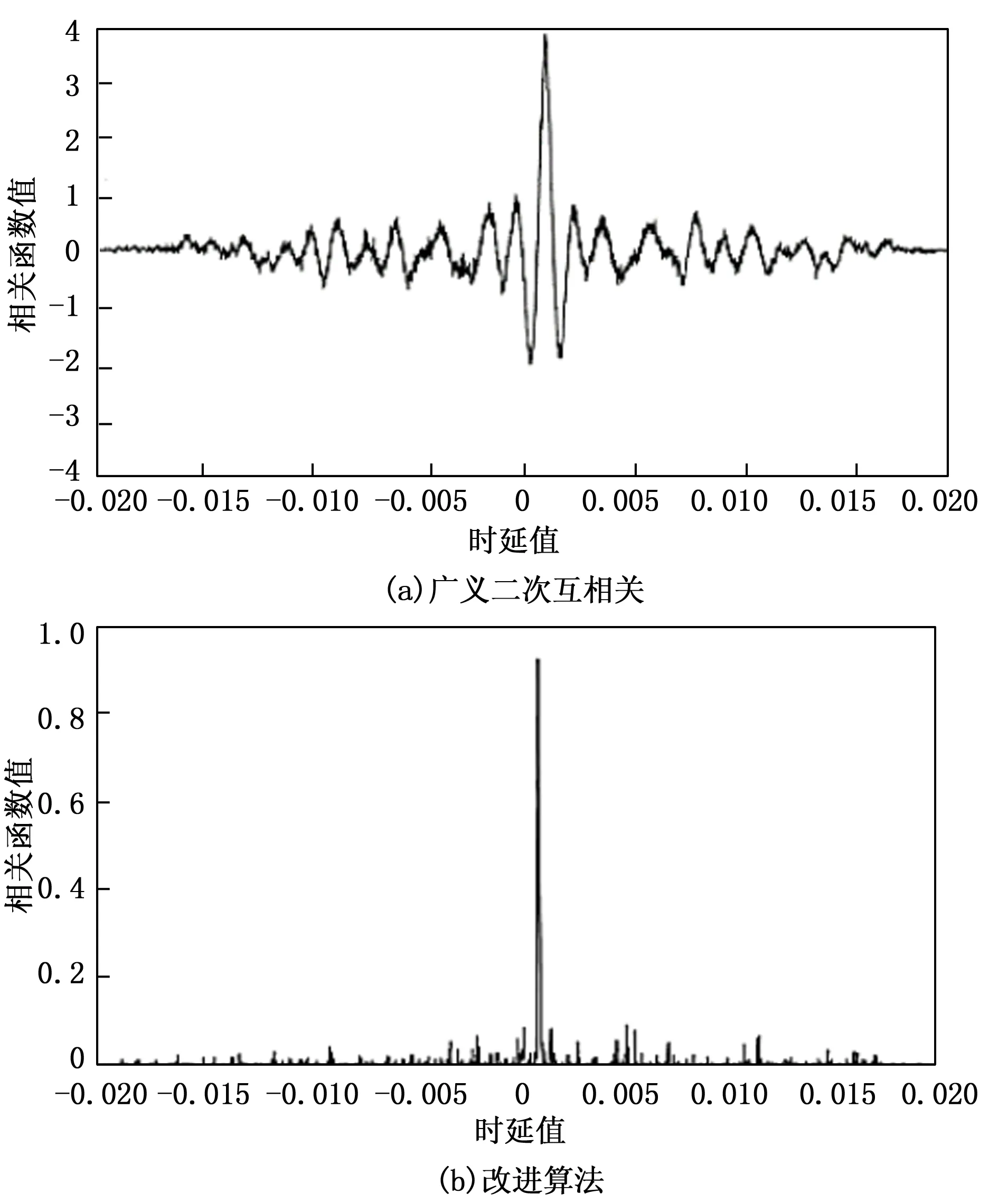
图9 SNR=0 dB时两种算法的时延估计结果

由图6可知，当信噪为0 dB时，广义二次互相关和改进的广义二次互相关算法计算的相关函数都有明显的主峰，时延估计的性能基本相同，都可以精确地估算出时延值；当信噪比为-5 dB时，广义二次互相关获得的互相关函数图出现多个干扰峰，主峰不够突出，改进算法的相关函数图主峰依旧明显；当信噪比为-15 dB时，广义二次互相关算法的真实峰值已经被淹没，广而使用改进的广义二次互相关算法获得的互相关函数仅出现了少许干扰峰，最大干扰峰值不到主峰值的1/2,主峰依然很明显。两种算法分别在不同信噪下获得的10次时延估计均值如表1所示。

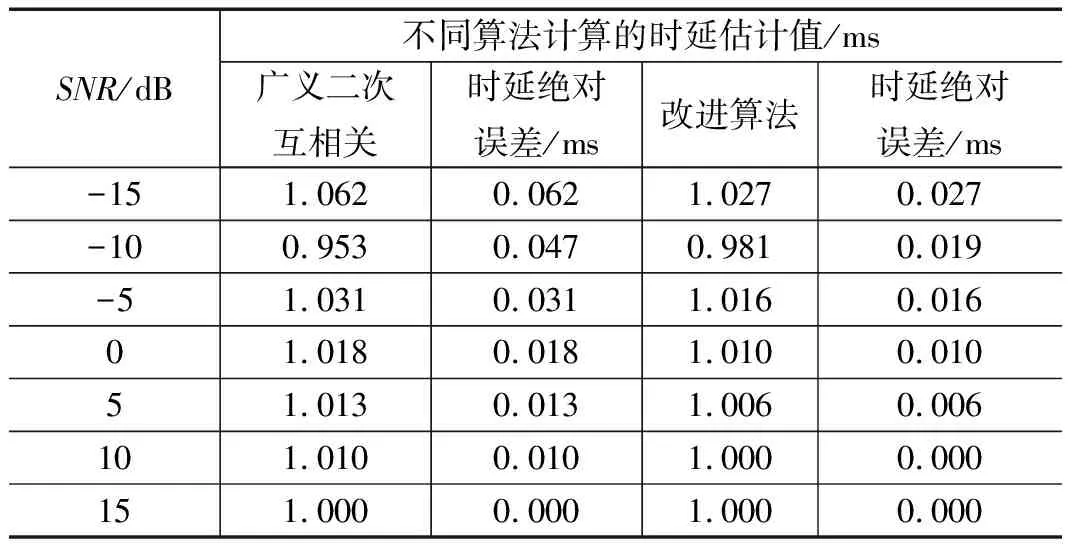
表1 不同信噪比下的时延估计值

由表1可知，相比广义二次互相关算法，改进算法在低信噪比情况下的时延估计性能明显提升，当SNR大于-10 dB时,时延估计误差小于20 μs，该算法可以满足立体六元声光阵列在低信噪比的情况下具有较高的俯仰角测试精度。

为了进一步验证声光阵列结构的实用性以及改进后的广义互相关算法的有效性，在空旷的户外对声光阵列以及算法进行炸高测量实验验证，声光阵列实物如图10所示。

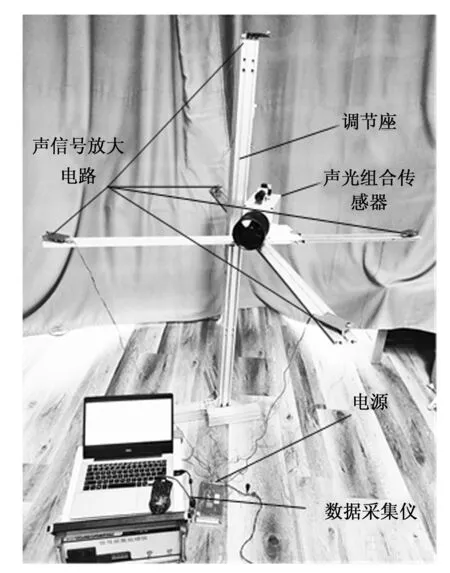
图10 声光阵列实物图

以全站仪测量值作为炸点高度得真值，为了避免因全站仪的不确定因素导致的实验结果存在误差，故选用两套全站仪同时测量炸点高度值取其平均值，在同一环境下使用声光阵列测量炸点高度，阵元间距设为2.2 m，数据采集卡的采样频率设置为1 MHz,采样位数为16位，采样点数设为1×106个，选取10个不同高度的位置进行炸高测量，每个位置做3次试验取平均值，最终测量的炸点的俯仰角及高度等数据如表2所示。

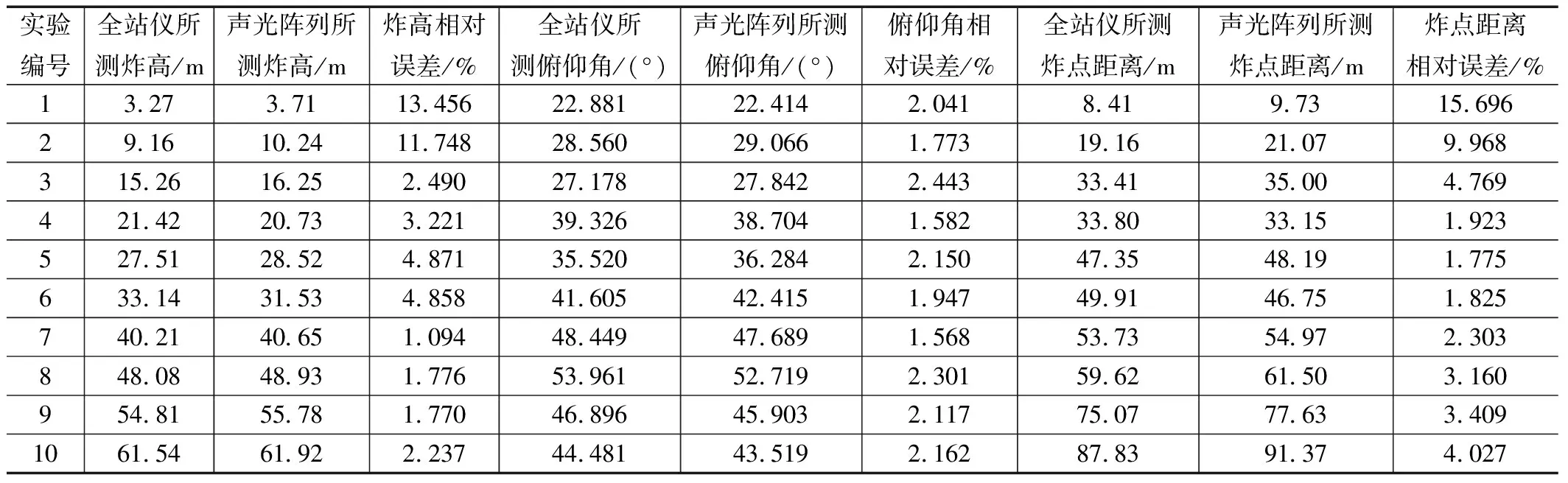
表2 声源高度测量实验数据

对表2数据进行分析可知，使用立体六元声光阵列测量炸高范围为(20 m,60 m)的炸点距离误差小于4%，与上述仿真结果一致；同时该基阵测试的声源位置的俯仰角相对误差小于2.5%、炸高测试误差小于5%，实验验证本文所提立体六元声光阵列可以有效的应用于炸高测量中。

5 结束语

本文提出了一种基于声光阵列的炸高测量技术，该方法通过测量爆炸声音到达不同传感器的声程差和声光信号到达测量基阵的时延估计值，实现单基阵测量炸点高度。经仿真分析，该声光阵列适用于测量高度范围为20～60 m内的炸点高度，测量时应确保阵元间距大于2 m，时延估计误差小于20 μs，声光信号到达基阵时延估计误差绝对值不高于4 ms。

除此之外，本文对广义二次互相关算法进行了改进，通过理论分析与实验验证了改进后的广义二次互相关算法在高信噪比的环境下可以得到精确的时延值，在低信噪比下，该算法获得时延估计相对误差小于3%，相比改进前时延估计提高了一倍,最终实现炸高测量偏差在5%之内，具有较高的测试精度,可以应用于靶场炸高测量中。