边界非线性结构的随机振动响应线性估计
彭扬林,刘洪英,董 睿,蔡红华,赵亚雄,石 蒙
(中国航天员科研训练中心,北京 100094)
1 引言
机械结构在工程应用过程中,存在大量受随机载荷作用的场合。所以在随机载荷作用下,结构的强度、刚度以及疲劳等问题,在结构设计阶段都需要高度重视。目前,利用有限单元法分析复杂结构的随机振动响应,已成为结构工程实践中广泛使用的一种数值计算解决方法。常见的商用数值计算软件均可计算结构的随机振动响应,其随机振动分析是一种基于概率统计学的谱分析技术,但是这种谱分析运算只能进行线性系统的数值计算。
机械结构中,含有各种非线性因素:材料非线性、几何非线性以及边界非线性等。自然界不存在绝对的线性系统,不同系统中,只是非线性特性强弱不同。非线性特性强时,多数情况下和线性模型的预测结果差异较大。
对于非线性随机振动响应分析已有较多的研究,主要集中在理论解法、近似解法和数值模拟解法三个方面,如FPK方程法、随机平均法、等效线性化方法、蒙特卡罗(Monte-Carlo)模拟法、马尔可夫(Markov)方法和摄动法等。大多数的研究方法,或者以理论分析为主,或者难以适用于多自由度系统。相应的算法,并未应用于成熟的工业软件中,在工程实践中的应用有限。
针对某航天组件结构的边界非线性,采用极限边界条件进行线性化数值模拟及估算,并进行相应的振动试验验证,解决了设计过程中非线性随机振动的响应估算问题,保障了产品的研制进度,有效地推进产品的设计改进过程。
2 产品结构及问题描述
本文所探讨的结构如图1所示,该结构包括腔体、组件A、组件及法兰连接件。该组件右端和腔体通过法兰连接,左侧和腔体上的定位环为间隙配合,如图1右下角的局部视图,其余区域组件和腔体之间沿径向存在间隙。

图 1 结构整体三维模型剖视图
该组件的三维模型如图2所示,产品研制初期,通过随机振动力学环境试验考核后发现,图2中关注的M2螺钉出现明显弯曲。也就是原有的M2螺钉的强度不够,随机振动试验过程中,螺钉截面上受到的应力较大程度上超过材料的屈服强度。为了解决这一问题,提出将原有M2螺钉更换为M3螺钉的方案,减少其他零部件的改动。

图 2 组件三维模型图
航天产品由于研制成本高、研制周期长的特点,导致试验验证的机会较少。仅评估将原有M2螺钉更换为M3螺钉,也会导致图2中桶2、连接法兰以及内部部分零部件的更改。为了加快验证周期、减少试制成本、降低改进风险,决定通过数值计算的方式来进行随机振动激励下的强度评估。
3 分析建模
锁紧螺母外圈和腔体定位环之间为间隙配合,间隙配合如图1所示,单侧设计间隙约为 0.035~0.080mm。由于间隙较小,在随机振动激励作用下,锁紧螺母和定位环之间在时间历程上,可能会不断出现接触和分离的情况,这是一个强非线性过程,常见的基于频域谱分析的随机振动响应分析难以模拟这种非线性的过程。这个非线性过程存在两种极限边界,极限边界1是锁紧螺母和定位环始终接触,存在轴向和切向的自由度,当振动幅度较大时符合这种情况;极限边界2是锁紧螺母这一端完全处于自由状态,定位环对其无约束,当振动幅度较小时符合这种情况。实际的振动过程应该介于这两者之间。
(1)模型简化
为了兼顾计算效率、模型规模和计算准确度,必须对现有结构进行合理的简化。
有限元建模方式及主要简化内容如下:
1)组件中非承力零部件删除;
2)除关注的螺钉采用实体建模,其他的螺钉均采用线体建模;
3)组件内部的薄壁零件采用壳单元进行建模;
4)对于工艺上考虑的结构倒角、圆角和微孔等局部细小特征进行删除处理;
5)对于零件删除、结构简化引起的质量差异采用分布质量附加在模型上。
(2)网格划分及边界条件
网格划分以四面体网格为主,形状规则的零部件采用六面体网格划分,面体采用四边形网格划分;对于不影响关注螺钉受力的零部件采用粗网格,关注螺钉附近区域的网格进行加密处理。网格划分后的有限元模型如图3所示。

图 3 组件有限元模型图
如前文描述,锁紧螺母一端的边界条件存在不确定性,所以对两种极限的边界条件均进行数值计算。极限边界1:锁紧螺母端受约束时,定位环外圈固定约束,定位环内圈和锁紧螺母之间沿径向约束,保持轴向和切向的自由度,法兰局部区域固定约束。极限边界2:锁紧螺母端处于自由状态时,模型的边界为法兰局部区域固定约束。
4 计算结果及讨论
该组件安装位置处,三个方向上的随机激励功率谱密度曲线如图4所示,对应的均方根加速度值分别为10.2g
、10.1g
和12.2g
。在进行数值模拟计算时,分别以图4中的曲线作为输入激励。
图 4 随机振动响应计算输入激励
为了能够定量估算随机振动激励下,产品的响应及应力水平,对关注螺钉使用M3和M2螺钉连接以及对两种极限边界情况下的四种工况进行计算。
(1)M2螺钉计算
在如图4所示的激励条件下,M2螺钉连接时,关注螺钉截面上的3σ
准则平均等效应力,M2螺钉截面的平均等效应力见表1。表 1 M2螺钉截面的平均等效应力(单位:MPa)
?
由表1可知,两种极限边界条件下,X
向和Z
向的应力值差异很大,这就是该边界非线性不能用线性计算去代替的原因。极限边界2条件下计算得到的锁紧螺母上位移在三个方向上的最大值分别为:0.208 mm、0.001 mm和0.118 mm。X
向和Z
向位移值均大于锁紧螺母和定位环设计公差0.08 mm,边界的两种极限状态在振动过程中均会发生。(2)M3螺钉计算
在如图4所示的激励条件下,M3螺钉连接时,关注螺钉截面上的3σ
准则平均等效应力,M3螺钉截面的平均等效应力见表2。表 2 M3螺钉截面的平均等效应力(单位:MPa)
?
相比于M2螺钉连接状态,M3螺钉连接时螺钉上的平均等效应力有较大幅度的下降。
(3)等效应力分析
螺钉材料的屈服强度为170 MPa,抗拉强度为485 MPa。M2螺钉在两种极限边界条件下,仿真计算得到的平均等效应力的最大值分别为115.9 MPa和869.9 MPa。由于实际试验中,M2螺钉发生弯曲,但并未出现断裂的裂纹,所以实际试验中,螺钉截面的平均等效应力应位于170~373 MPa(上文计算结果中,截面上的应力范围约为平均应力的±30%,局部达到抗拉强度即有可能出现裂纹。根据平均应力的范围和抗拉强度的安全系数约为1.3,所以按照485 MPa除以1.3得到373 MPa)。所以,试验中的实际应力值,位于两种极限边界条件下的仿真值之间。
由表2可知,M3螺钉两种极限边界计算得到的最大平均等效应力为47.4 MPa和349.5 MPa。不同螺钉及边界条件下的仿真计算应力值和实际应力之间的关系如图5所示。可以近似认为,随机振动过程中M3螺钉截面上的实际平均等效应力位于图中σ
和σ
之间。根据图中的几何关系,可以计算得到σ
=69 MPa,σ
=150.4 MPa,也就是M3螺钉截面上的平均等效应力范围为69~150.4 MPa。另外,3σ
准则的等效应力评估本身偏保守,所以,根据等效应力分析可知M3螺钉随机振动过程中的应力小于其屈服强度,满足设计的使用要求。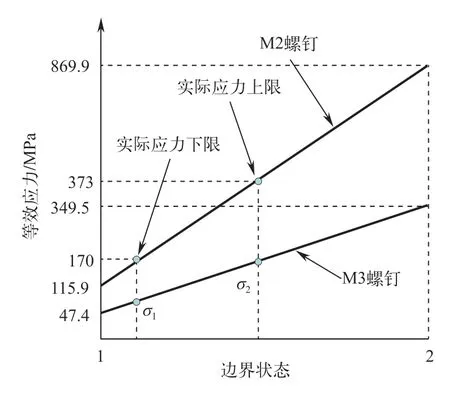
图 5 不同螺钉及边界的等效应力关系
5 试验验证
为了验证数值计算的结果,对改进后的组件及腔体结构进行随机振动力学试验。试验过程中组件安装在腔体内,通过专用试验夹具安装于振动台的水平滑台上,试验实施过程如图6所示。

图 6 随机振动试验验证
组件在进行随机振动试验之后,对其所在系统的性能和结构外观进行检查。检查结果显示,系统性能运行良好,组件和关注螺钉外观完好未发生变形。充分验证了改进设计方案的有效性,以及数值计算结果的有效性。
6 结束语
通过数值计算方法,使用线性随机振动响应分析对非线性随机振动响应进行估算,达到了改进方案验证的目的。得到如下结论:
1)有限元数值计算方法,可以有效地计算结构的随机振动响应,加快设计效率,减少研制成本。
2)非线性随机振动响应计算成本高、应用要求高,工程应用中可以通过线性近似或估算的方法结合试验验证来进行。
3)通过已有的试验数据和边界极限条件,可以对类似改进的工程应用进行有效的数值估算。本文的数值计算和振动试验,充分验证了该计算方法用于改进后结构响应预测的有效性。

