基于RBF 神经网络的四旋翼无人机姿态控制

甘顺顺，许宝杰，黄小龙

（北京信息科技大学机电工程学院，北京 100192）

0 引言

四旋翼无人机作为一种可垂直起降的无人机设备，具有灵活性强、成本低、易于操控等特点。随着集成电路技术、通讯、导航等新技术发展，近年来四旋翼无人机在军事、消防、救援、物流等领域得到了广泛的应用。四旋翼无人机作为一种典型的多输入、多输出、强耦合、欠驱动的非线性系统，且由于外界扰动和系统建模不确定部分的影响，难以建立精确的数学模型[1]。

针对上述四旋翼无人机的特点，国内外研究者在无人机控制上提出了多种控制策略，主要有PID 控制[2]、滑模控制[3]、反步控制[4]、自扰抗控制[5]、预测控制[6]等等。终端滑模控（Terminal Slide Mode Control，以下简称TSM）在标准滑模控制（Slide Mode Control，以下简称SMC）基础上，通过在滑模面引入非线性函数，使得追踪误差在滑模面上能够在有限时间内收敛至零，达到对期望状态的完全追踪[7]。TSM 在远离稳态时，无法保证控制系统在短时间内快速收敛，且在接近稳态时存在有奇异性问题。Yu X，Man Z 等人提出一种快速终端滑模控制（Fast terminal sliding mode control）方法，可使控制系统以更快速度收敛[8]。Yu X基于TSM，提出一种非奇异终端滑模控制（Nonsingular Terminal Slide Mode Control）方法，解决终端滑模控制在接近稳态的奇异性问题，但系统收敛速度与TSM 类似[9]。李升波等人基于NTSM 提出了一种非奇异快速终端滑模控制（Nonsingular Fast Terminal Slide Mode Control，简称NFTSM）方法，保证控制系统能在有限时间内收敛至期望状态，同时避免出现奇异性问题[10]。

神经网络具有很强的自学习能力、非线性映射能力，可以逼近任意非线性函数，被广泛应用于复杂系统的控制中。径向基神经网络（Radial Basis Function Neural Network，简称RBF 神经网络）是一类特殊的神经网络结构，在应用于系统控制时，可基于Lyapunov稳定性定理设计自适应率，用以迭代更新RBF 神经网络的链接权重。相对于采用梯度下降法调整神经网络权重，可有效避免RBF 神经网络陷入局部最优解，保证控制系统的稳定性[11]。Wang S 利用RBF 神经网络逼近机械臂系统不确定部分及外界扰动，对机械臂的控制取得较好的控制效果[12]。韩壮业等人利用RBF 神经网络对四旋翼无人机模型进行逼近，以实现自适应控制，达到较好轨迹追踪控制和抑制扰动的效果[13]。

针对四旋翼无人机姿态系统存在难以建立精确动力学模型及外界未知扰动的问题，本文提出一种基于RBF 神经网络自适应非奇异快速终端滑模控制方法（简称ANFTSMNN），利用RBF 神经网络对系统不确定部分及外界扰动组成的总扰动进行实时在线逼近，并将逼近结果反馈给控制器，使控制系统具有强自适应性。通过Matlab/Simulink 仿真验证ANFTSMNN 方法在无人机姿态控制系统的稳定性和性能优势。

1 无人机动力学模型

以十字形四旋翼无人机姿态系统研究对象，将四旋翼无人机模型简化为如图1 所示的结构示意图。四旋翼无人机在飞行过程中，四旋翼无人机通过让电机产生转速差，产生驱动力矩，进而改变无人机的位姿。

图1 四旋翼无人机结构简图

四旋翼无人机姿态系统模型满足如下假设：

假设1：（1）四旋翼无人机为刚性结构且结构对称，其质心与机体坐标系重合；（2）每个旋翼产生的升力和受到的反扭矩都与旋翼的转速平方成正比力；（3）四旋翼无人机角速度为姿态角的导数。

如图1 所示，建立惯性坐标系E=（ex，ey，ez）与无人机机体坐标系B=（bx，by，bz），用以描述无人机在空间中的位姿。φ、θ、ψ分别无人机的翻滚角、俯仰角、偏航角，Ω1、Ω2、Ω3、Ω4为电机M1、M2、M3、M4的转速。根据牛顿-欧拉方程建立四旋翼无人机姿态系统的数学模型，如式（1）所示。

式（1）中Ixx、Iyy、Izz分别为无人机绕机体坐标系E的bx、by、bz轴的转动惯量；l为四旋翼无人机质心到各旋翼中心的距离，d1（t）、d2（t）、d3（t）表示外界扰动，且≤dimax，i=1，2，3。U2、U3、U4为翻滚角、俯仰角、偏航角通道控制量输入，其具体表达式如下式（2）所示：

式（2）中，b、d分别为无人机旋翼升力系数和反扭矩系数。

由于在四旋翼无人机姿态系统中，翻滚角、俯仰角与偏航角通道相对独立，在考虑无人机模型不确定部分及外界扰动的前提下，将无人机姿态系统表示为如下式（3）所示的状态空间表达式。

式（3）可视为三个相对独立的二阶SISO 系统构成，其中将系统不确定部分和外界扰动之和定义为系统的总扰动，定义各个通道的总扰动为：Di（X，t）=△fi（X）+di（t），t=1，2，3，其中△fi（X）为系统不确部分，总扰动Di（X，t）满足如下假设：

假设2：外界扰动di（t）有界，则总扰动Di（X，t）有界，即≤Dimax。

2 自适应控制器设计

以下式（4）中典型二阶SISO 系统为研究对象，设计ANFTSMNN 控制器，并通过Lyapunov 稳定性定理，设计自适应律，证明该控制方法的稳定性。

式（4）中，D（x，t）=f（X）+d（t）为系统总扰动，由系统不确定部分△f（X）及外界扰动d（t）构成。D（x，t）满足假设2，即≤Dmax。基于RBF 神经网络的非奇异快速终端滑模控制器对二阶SISO 系统进行控制的原理图如图2 所示。

图2 ANFTSMNN 控制原理图

ANFTSMNN 控制器根据期望状态xd与当前状态x的追踪误差，利用RBF 神经网络对总扰动D（x，t）进行实时逼近，并将D（x，t）的估计值反馈给滑模控制器，用以补偿总扰动对系统的影响，实现对期望状态的自适应完全追踪。以下，将详细介绍ANFTSMNN控制器的设计过程。

2.1 非奇异快速终端滑模控制控制器初步设计

结合式（4）中的阶SISO 系统，定义追踪误差：

式（5）中，yd为系统期望输出。根据式（5），可将式（4）表示为：

式（6）中，F（x）=f（x）-=b。定义非奇异快速终端滑模面（简称，NFTSM 滑模面）：

式（7）中k1、k2＞0，1 ＜β ＜2，且α＞β。NFTSM 滑模面的子项在系统状态远离稳态时，能够保证系统以较高速度收敛至系统稳态，在系统趋近于系统稳态时，子项起主导作用，能够保证系统在有限时间内收敛[14]。结合式（6），对式（7）求导得：

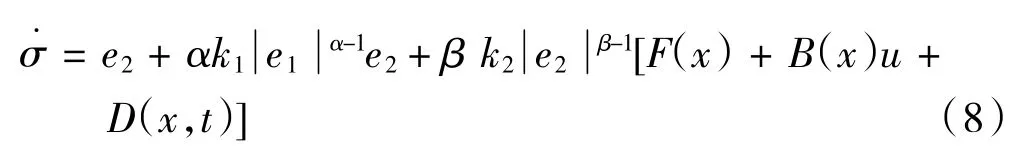
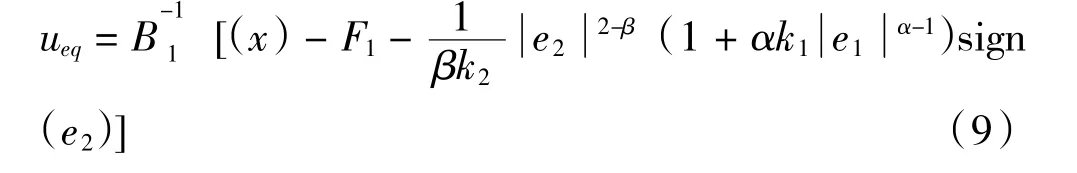
为保证系统在外界扰动以及系统不确定项的影响下系统的鲁棒性，设计切换控制率usw：

式（10）中η1、η1＞0，可得该系统的控制率为：

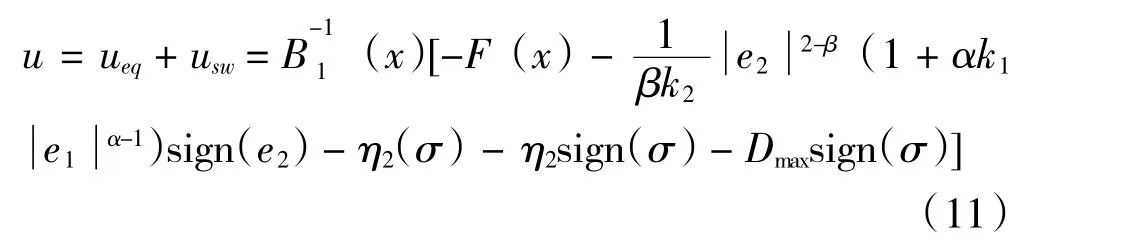
其中ueq为等效控制项，用以保证系统的追踪误差快速收敛至0，使得系统的状态始终在滑模面上；usw为鲁棒控制项，用以抑制总扰动对系统的影响，保证系统的状态不离开滑模面[15]。

定义Lyapunov 函数：

结合式（8），对式（12）求导得：

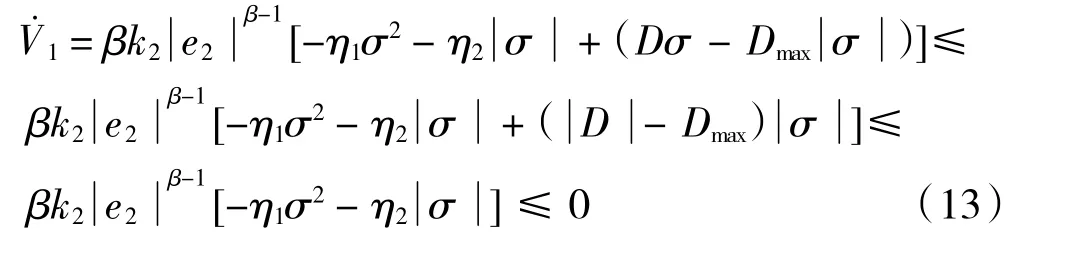
由V1≥0 且≤0，根据Lyapunov 稳定性定理，可知该控制系统渐进稳定，系统追踪误差渐进收敛于0。

2.2 ANFTSMNN 控制器设计

RBF 神经元网络结构如图3 所示，其基本结构由输入层、隐含层、输出层构成。其中，RBF 神经网络的输入层有m个节点，输入层的输入向量为x=[x1，x2，…，xm]；RBF 神经网络的隐含层有n个节点，RBF神经网络的隐含层的激活函数为高斯基函数，隐含层输出为h（x）=[h1（x），h2（x），…，hj（x），…，hn（x）]T，RBF 神经元网络输出层与隐含层之间的连接权重W=[W1，W1，…，Wn]T。RBF 神经网络逼近位置模型算法为：

图3 RBF 神经网络结构

根据Lyapunov 稳定性定理设计自适应率，用以迭代调整更新RBF 神经元网络连接权重和神经元网络逼近误差，其自适应率为：

对式（25）两边同时进行积分，设为误差由初始状态e1≠0，V2（0）≠0 收敛至e1=0，V2（tr）=0 状态所用时间。对式（25）两边进行积分得：

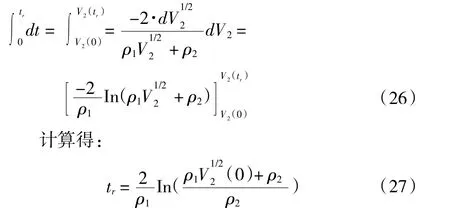
综上所述，基于RBF 的神经网络的非奇异快速滑模控制方法能，保证控制系统渐进稳定，使得系统的追踪误差在有限时间tr内收敛至0。

3 仿真实验

在Matlab/Simulink 环境中，搭建四旋翼无人机姿态控制系统模型，分别设置两组对照实验：一组用于研究ANFTSMNN 控制方法在不同参数配置下，对RBF 神经网络逼近未知模型的能力的影响；另一组用于研究基于3.1 中NFTSM 方法、3.2 中的ANFTSMNN 方法和SMC 方法对无人机姿态系统进行控制的性能表现。

3.1 仿真实验条件设定

仿真实验中四旋翼无人机系统基本参数如表1。

表1 无人机模型参数

定义翻滚角、俯仰角、偏航角初始状态为X=（0，0，0，0，0，0），各姿态角轨迹追踪期望值为：

式（28）中，t为当前时间。定义四旋翼无人机姿态系统的初始总扰动为：

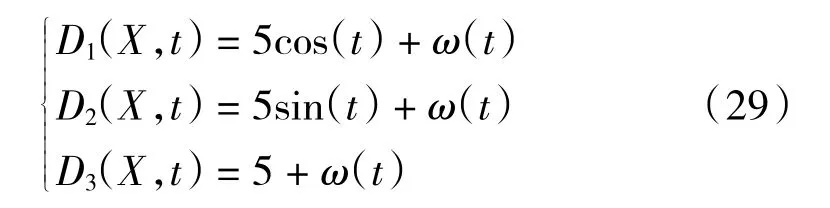
式（29）中，ω（t）幅值为0.5，均值为0 的高斯白噪声，用以模拟外界不规则扰动。4.2 RBF 神经网络逼近未知模型研究

文献[12]、[13]中，利用RBF 神经网络对未知模型进行逼近时，不对神经网络逼近误差δ进行估计，仅以神经网络输出作为估计值。利用该方法，根据3.2中的控制设计过程，对式（4）中D（x，t）中进行逼近，其估计项及自适应律如下：

根据4.1 中表1 仿真参数设置，保持其他条件基本不变，以偏航通道为研究对象，研究神经网络逼近误差项及γ1、γ2对逼近未知模型能力表现的影响，具体取值如表2 所示。设置仿真时间t=15 s，为便于研究分析，保持式（28）中总扰动初始D1（X，t）、D2（X，t）不变，令初始D3（X，t），在t=10 s 时，在俯仰通道上再施加5 rad/s2的外界突变扰动。不同参数条件下的实验结果如图4 所示。

根据图4，对其进行定量分析，其具体结果如表2 所示。其中所示逼近初始所用时间，表示在t=10 s时，突变外界扰动影响下逼近所用时间。

图4 不同参数下逼近未知模型仿真结果

表2 总扰动逼近时间

根据图3 和表2 实验结果可知，相对于式（29）中逼近未知模型的方法，神经网络逼近误差估计项能有效提升RBF 神经网络逼近未知模型的速度。取参数γ1=600，γ2=600 相对于γ2=600 但无误差逼近估计项，t1缩短了48.33%，t2缩短了15.00%。γ1、γ2分别取不同值，研究γ1、γ2对神经网络逼近未知模型的影响。取γ2=600，分别取300 和600，由仿真结果可知，逼近D3（X，t）的所用时间的随γ2的增大而缩短。其中，取γ2=600 相较于γ2=300 的逼近时间t1缩短了43.89%，t2缩短了10.52%。取γ2=600，γ1分别取600 和1000，仿真结果表明增大γ1可有效缩短逼近D3（X，t）所用时间，其中t1缩短了60.59%，t2缩短了29.41%。

3.2 无人机仿真实验分析

根据4.1 中无人机仿真条件，设置仿真时间t=30 s，在t=15 时，在翻滚角、俯仰角、偏航角通道上分别施加0.2 N/m、0.2 N/m、0.5 N/m 的阶跃响应作为突变外界扰动，研究控制系统在外界突变扰动的下的鲁棒性及稳定性，以下对仿真结果进行分析。

3.2.1 总扰动逼近效果分析

根据上述仿真条件，对翻滚角、俯仰角、偏航角通道上的总扰动D1（X，t）、D2（X，t）、D3（X，t）逼近的估计值效果进行分析，其仿真结果图像如图5所示。

图5 各通道总扰动逼近仿真实验

根据图5 可知，ANFTSMNN 控制器对无人机在翻滚角、俯仰角、偏航角通道的总扰动逼近时，即使在有较强白噪声干扰下，在出现短暂的超调量后，快速的逼近真实总扰动。对于外界白噪声干扰，呈现出一定滤波能力，使得ANFTSMNN 控制器能够有效补偿白噪声造成的干扰。

3.2.2 期望值追踪效果分析

对式（29）中的无人机期望姿态轨迹进行追踪，基于SMC、NFTSM、ANFTSMNN 三种不同控制方法的姿态角追踪效果如图6 所示。

图6 三种不同控制方法的资态角追踪效果

结合图6 对姿态角追踪进行综合分析。根据图5翻滚角通道轨迹追踪图（a），由左侧放大图可知，由初始状态收敛至期望轨迹，SMC 方法耗时约1.18 s，NFTSM 和ANFTSMNN 方法收敛速度近似，在t=0.78 s 时收敛，ANFTSMNN 方法相较于SMC 收敛时间缩短了33.90%。且收敛后ANFTSMNN 方法收敛后追踪误差最小，追踪效果优于NFTSM，远好于SMC方法。在t=15 s 时，突变外界扰动的影响下，由图6（a）右侧放大图，可见ANFTSMNN 方法对外界扰动影响不明显，且在一定时间后重新收敛至期望值，SMC 及NFTSM 均受到外界扰动影响明显，且SMC方法受到突变扰动影响着很大。

翻滚角追踪的初始误差为0°，三种控制方法初始时便可实现控制系统的快收敛。由图6（b）左上方的放大图可知，ANFTSMNN 目标追踪效果优于SMC及NFTSM，即使在后两者出现最大追踪误差处，ANFTSMNN 依旧可以很小的追踪误差近似完全拟合。由图6（b）右侧的放大图可知，在突变外界扰动影响下，ANFTSMNN 方法近似拟合于期望轨迹曲线，而其余两种方法则出均现轨迹追踪误差。

偏航角追踪期望值为固定值，由图5（c）可知SMC 控制方法在t=1.65 s 收敛于期望值，收敛后存在约-0.1148°的稳态误差，在t=15 s，0.5 N/m 的阶跃响应扰动影响下，在轻微波动过后收敛，但会产生静态误差。相对于SMC 方法，由于ANFTSMNN 及NFTSM 方法参数基本相同，二者收敛速近似，在t=1.18s 实现收敛，相对于SMC 所用时间缩短了28.48%。但NFTSM 方法与SMC 方法类似，由于在控制器，设计建模中存在未知部分及外界扰动存在，因而引起一定静态误差。而ANFTSMNN 方法在出现约0.01°超调量后，于t=16.64 s 重新收敛至期望轨迹，接近于完全拟合。

综上所述，ANFTSMNN 控制方法，相对于SMC、NFTSM 方法，在无人机姿态系统控制中具有明显优势。能够保证无人机姿态角的追踪误差快速收敛至0，具有很强的鲁棒性，能有效抑制外界扰动和系统不确定部分对无人机造成的影响，具备强自适应能力。

4 结束语

针对四旋翼无人机姿态系统难以建立精确模型问题，其建模中存在不确定部分及外界扰动影响，将非奇异快速终端滑模控制方法与RBF 神经网络结合，设计基于RBF 神经网络的自适应非奇异快速终端滑模控制器，并将其应用于无人机姿态控制中。仿真实验结果表明，以RBF 神经网络输出及神经网络逼近误差估计值之和为未知模型的估计值的方式，可明显提升RBF 神经网络逼近未知模型的速度，同时有效抑制未知模型白噪声扰动影响，起到滤波的作用。相对于非奇异快速终端滑模控制器及标准滑模控制控制器，通过设置最大扰动上界保证控制系统的稳定性，基于RBF 神经网络的自适应非奇异快速终端滑模控制器，利用RBF 神经网络逼近系统中的不确定部分及外界扰动组成的总扰动，并将其估计值反馈给控制器，补偿总扰动的干扰，实现自适应控制。无人机姿态角追踪仿真实验结果表明，基于RBF 神经网络的自适应非奇异快速终端滑模控制方法具有鲁棒性强、响应速度快、自适应能力强、无稳态误差的特点。