改进灰狼算法及其在港口泊位调度中的应用
李长安,谢宗奎,吴忠强,张立杰
(1. 先进锻压成形技术与科学教育部重点实验室(燕山大学),河北 秦皇岛 066004;2 .燕山大学 电气工程学院,河北 秦皇岛 066004;3. 河北省重型机械流体动力传输与控制重点实验室(燕山大学),河北 秦皇岛 066004;4.神华天津煤炭码头有限责任公司,天津 300457)
港口在全球经济贸易中发挥着重大作用,是海上运输的枢纽. 当一个港口在进行船舶货物的装卸与运输时,泊位直接面向船舶作业,其数量是有限的,因此如何合理安排泊位,提高港口装卸效率,进一步降低成本成为当前的研究热点. Etsuko等[1]指出,传统的泊位分配方法已阻碍大多数港口的发展,提出了以船舶停泊时间最少为目标函数的非线性整数规划模型,并将遗传算法(Genetic Algorithm ,GA)引入泊位调度优化中,通过大量的实验证明了GA算法的可行性. GA算法是一种较早的群集智能算法[2],以其高效性和稳定性的优势得到广泛的应用,同时也存在过早收敛以致求解精度低的不足.
为提高算法的寻优精度和优化效率,近年来研究人员提出多种群集智能算法. 黎成[3]在2010年通过模拟蝙蝠的捕食行为特征提出了蝙蝠算法(Bat-inspired Algorithm,BA). 2011年,刘长平等[4]通过模拟萤火虫发光特性提出萤火虫算法(Firefly Algorithm,FA);Pan等[5]通过模拟果蝇觅食行为提出果蝇算法(Fruit Fly Optimization Algorithm,FOA). 2012年Gandomi等[6]受磷虾个体的群体特征启发,提出磷虾群算法(Krill Herd Algorithm,KH). 2014年 Mirjalili等[7]通过模拟灰狼捕食猎物的行为机制提出灰狼优化算法(Gray Wolf Optimizer,GWO); Cuevas等[8]通过模拟社会蜘蛛协作行为,提出蜘蛛群算法(Social Spider Optimization,SSO-C). 2015 年Meng 等[9]通过模拟鸟群的群体行为,提出鸟群算法( Bird Swarm Algorithm, BSA). 2016年 WU等[10]通过模拟海豚的群体捕食行为提出海豚群算法(Dolphin Swarm Algorithm,DSA). 2017年Mirjalili 等[11]提出樽海鞘群算法(Salp Swarm algorithm, SSA). 2018年刘生建等[12]模仿狮群捕食行为提出狮群算法(Lion Swarm Optimization, LSO). 这些算法已被广泛应用到各个领域[13-14].
GWO算法自出现起,就以其原理简单、易于实现、可调参数少等优点受到研究者们的广泛关注,在函数优化方面具有很好的稳定性和寻优精度. 文献[15]指出,在面对复杂的优化问题时,GWO算法与大多智能算法相似,也存在易早熟、收敛精度低等缺陷. 为进一步提升GWO算法的收敛速度和寻优精度,增强算法的可靠性,更好地解决港口泊位动态调度问题,本文提出一种改进灰狼算法(Improved Gray Wolf Optimizer ,IGWO). 在生成初始种群时引入Sin混沌初始化[16],增强初始种群的均匀性;引入头狼引领策略,加快算法收敛,提高算法效率;引入合作竞争机制,提高个体间有效信息的利用率;在灰狼种群位置更新时引入自适应权值,以满足不同时期的寻优要求. 为验证IGWO算法的有效性,将IGWO算法与SSA算法、DSA算法、SSO-C算法、DSA算法、LSO算法及标准GWO算法进行对比实验,并将IGWO应用于港口泊位调度中,以证明该算法在港口泊位调度优化中的实用性和有效性.
1 GWO算法
GWO算法的主要思想如下:从待寻优空间的任意位置开始,将具有最优适应度值的个体设置为头狼α,适应度值排第2和第3的个体设置为下属狼β和普通狼δ,其余为底层狼ω. 在捕食过程中,首先由α、β和δ判断猎物所在位置并进行追捕;当发现猎物所在位置时,α、β和δ带领ω对猎物进行围剿,通过不断迭代搜索得到最优值.
在捕食的过程中,α、β和δ据猎物最近,首先要确定灰狼个体与α、β和δ之间的距离:
(1)
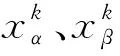
随后,狼群其他个体利用α、β和δ之间的位置判断猎物位置,对猎物进行围剿,该过程可描述为
(2)
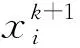
2 改进GWO算法
2.1 Sin混沌初始化
初始种群位置对算法的收敛速度和求解精度有很大的影响,甚至会导致寻优的失败. 在初始化的过程中,搜索空间的随机分布会使种群个体分布不均,多样性较差. 混沌映射是由确定性方程得到的具有随机性的运动状态,具有随机性、遍历性的特点. Logistic映射和Sin映射是混沌学中常用的两种映射,其映射表达式分别为
xn+1=μxn(1-xn),xn∈(0,1),
(3)
xn+1=sin(2/xn),xn∈(-1,1)∩xn≠0.
(4)
式(3)中,μ的取值范围是(0,4),在>3.6时产生混沌现象,产生的xn+1的范围为(0,1). 为比较上述两种混沌映射的混沌特性,利用式(3)和式(4)分别产生区间(-1,1)上的2维混沌解,如图1所示.
由图1可知,Logistic映射产生的混沌解遍历性较差,在空间中分布不均;与Logistic映射相比,Sin映射的混沌解在空间中分布均匀,具有更明显的混沌特性. 为使初始种群具有更好的遍历性和均匀性,引入Sin混沌映射进行初始化,以加快算法的收敛.
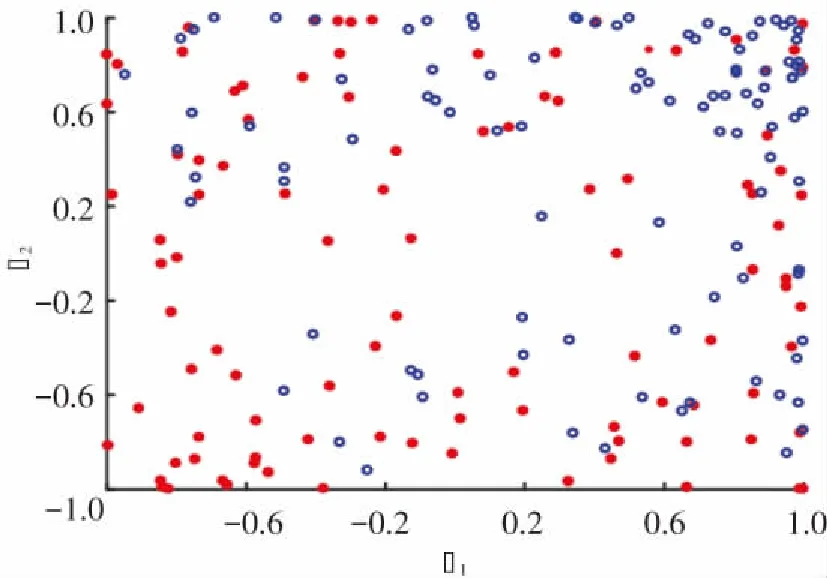
·Sin映射 ∘Logistic映射
2.2 头狼引领
由α、β、δ确定猎物所在位置后,底层狼ω随即对猎物进行围捕. 此时,狼群中头狼距猎物的距离最近,底层狼距头狼位置较远,包围过程中狼群围捕速度较慢. 若能缩短猎物与整个种群之间的相对距离,则能够加大猎捕的成功几率,提高算法的寻优速度,故引入头狼引领策略. 种群中每一只狼在围捕猎物前均按式(5)小步跟随头狼α进行移动,以缩短每只狼与猎物之间的距离.
(5)
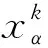
2.3 合作竞争机制
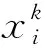
(6)
(7)

2.4 自适应惯性权值
为满足GWO算法在不同迭代周期的寻优要求,提高收敛速度和寻优精度,引入自适应惯性权值w,且
随着迭代次数的增大,w从1逐渐减小到0.
改进后位置更新如式(8)所示:
(8)
2.5 算法步骤
步骤1. 设置算法参数. 初始设置的参数主要有:种群数M,最大迭代次数T,维度D,求解空间的上限ub和下限lb.
步骤2. 进行混沌初始化,按式(4)生成初始种群.
步骤3. 计算种群中每个个体的适应度值,并选取适应值最小的3个个体的位置分别作为α、β和δ.
步骤4. 按式(5)执行头狼引领策略.
步骤5. 除α、β、δ的灰狼个体按式(6)、式(7)执行合作竞争机制.
步骤6. 根据式(1)计算其他灰狼与α、β、δ的距离. 根据式(8)和式(2)更新其他灰狼的位置.
步骤7. 若达到最大迭代次数,转至步骤9;否则转至步骤8.
步骤8. 每隔一定迭代次数,重新排序,确定灰狼的位置,转至步骤3.
步骤9. 输出当前最优解,算法结束.
3 IGWO算法的收敛性分析
为证明IGWO算法的有效性,采用Markov链对该算法的收敛性进行分析[18]. 设搜索空间为H,头狼引领、狼群互动和围攻等行为均会引起状态空间中的状态转移,设3个行为过程的转移矩阵分别为S、M和W,则定义IGWO的Markov链转移矩阵为
P=S×M×W.
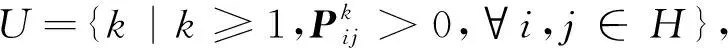
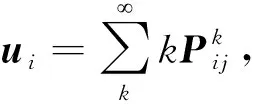
首先,证明IGWO的优化解序列是一个有限齐次Markov链. 设Qk={x1,x2,…,xN}为IGWO的第k代种群,N为灰狼种群大小,xi为第i只灰狼的状态. 因为灰狼种群Qk是有限的,所以该算法的解序列是有限Markov链. 其次,由于IGWO算法中头狼引领、狼群互动和围攻行为都是在独立随机过程中进行的,每次个体更新具有优胜选择的继承性,第k+1代种群的产生只与第k代群体有关,与各代群体之间的转移概率无关. 经过种群的位置更新,可以得到一组优化解序列. 因此,经过IGWO一系列独立随机的变换处理得到的优化解序列是一个有限齐次Markov链.
还需证明IGWO算法种群序列的Markov链是遍历链.
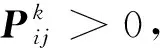
由于群体转移概率矩阵Pij=P{Qk+1=j|Qk=i,k≥1}只与状态i和j有关,且Qk>0,则群体转移概率矩阵P为正定矩阵. 由定义1可得,IGWO算法的种群序列为不可约的Markov链.
对于给定的k>0,由IGWO是不可约的Markov链可知,∃j∈H,使得Pij>0,又由定义2知k=1. 因此集合U的最大公约数为1,则IGWO为非周期不可约的Markov链.
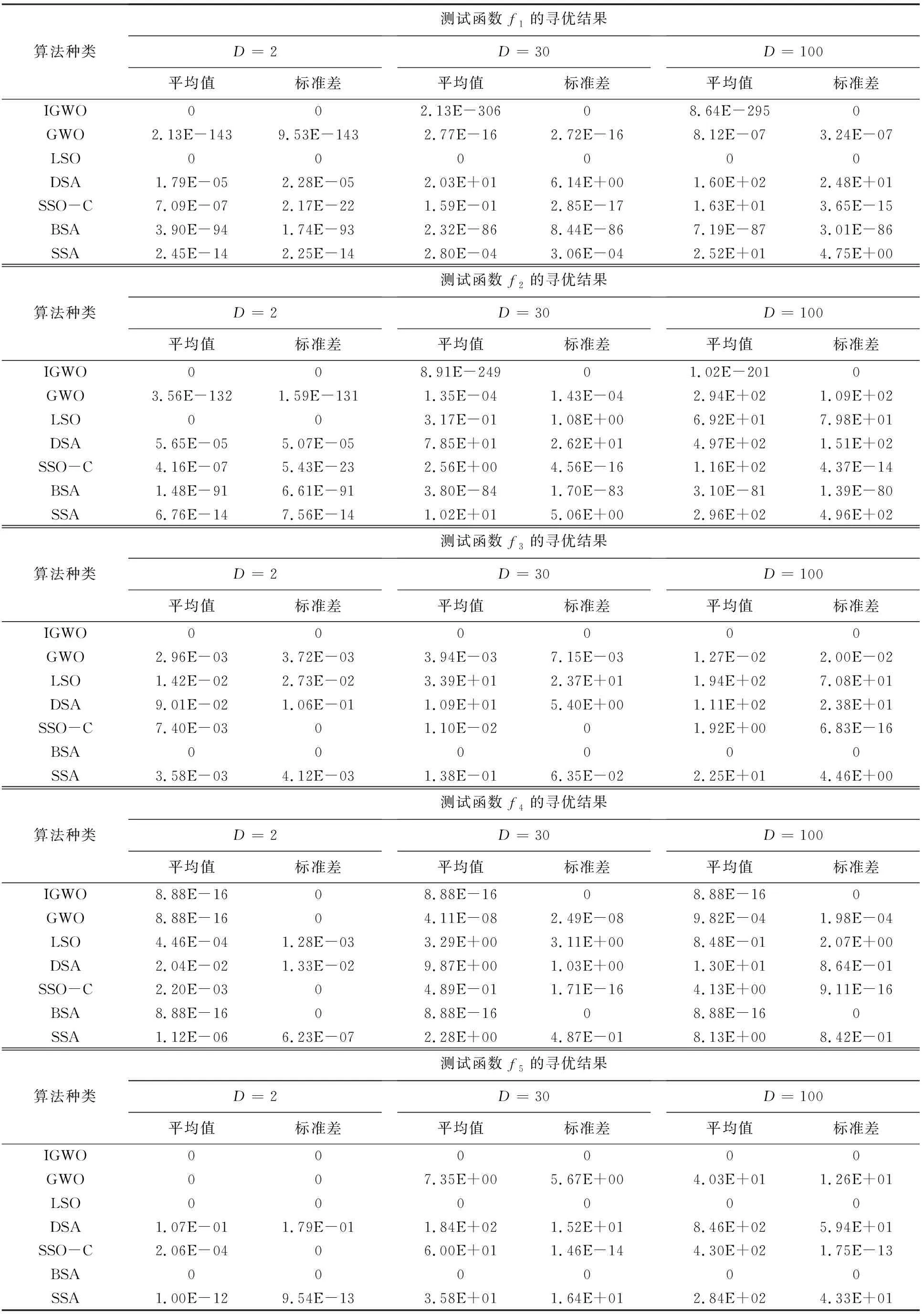
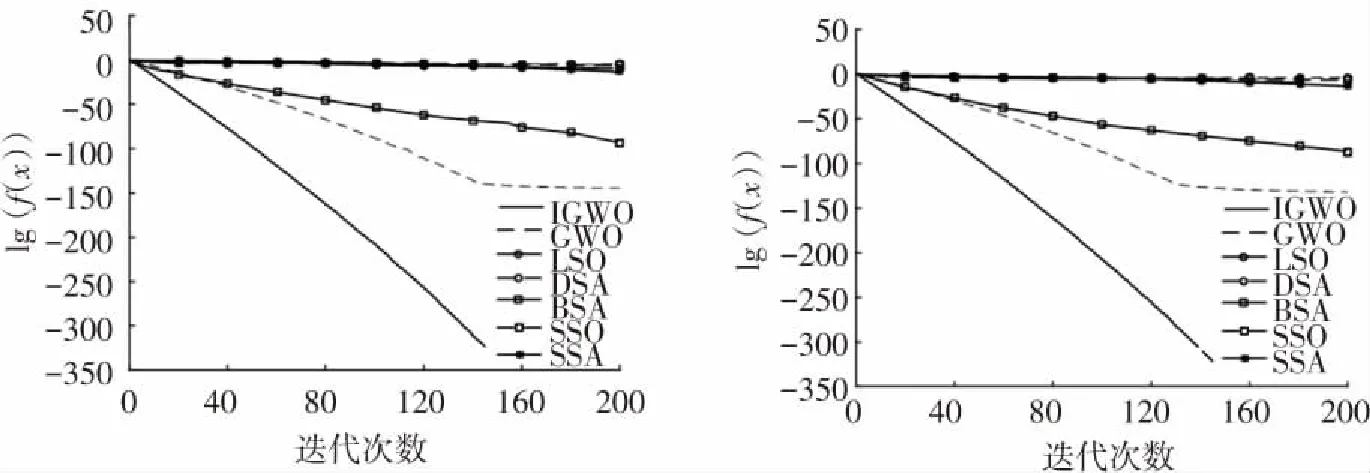
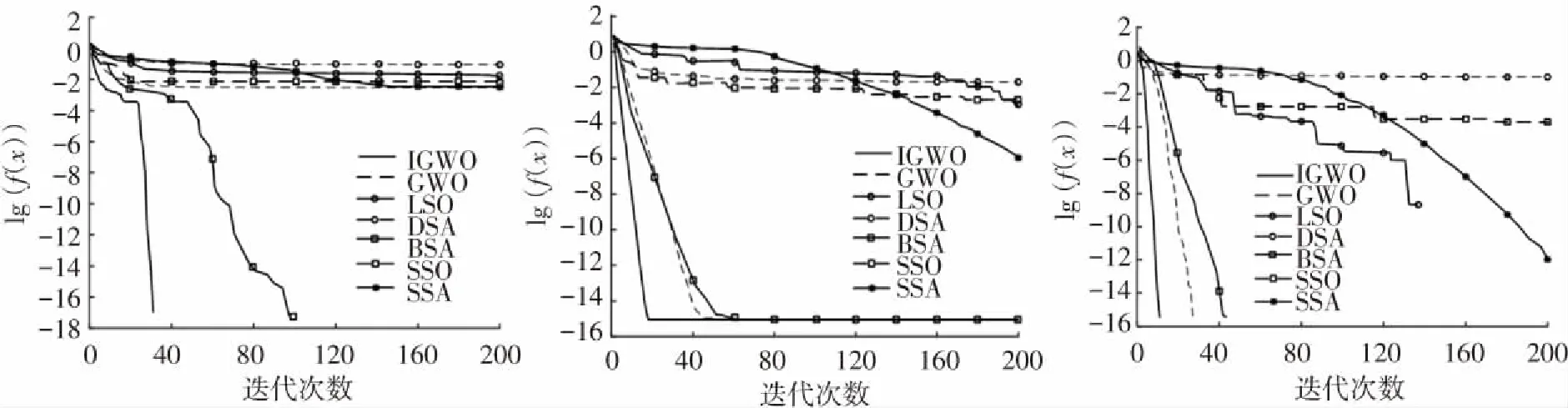
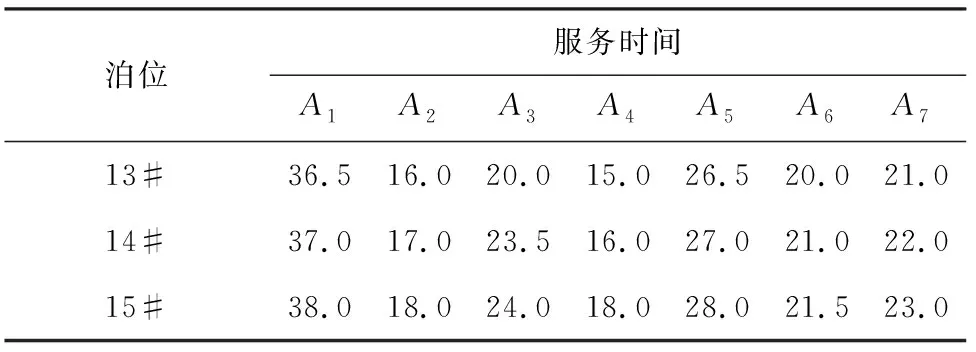
Pij为状态i经历各行为达到状态j的转移概率,由于转移矩阵S、M和W都处于(0,1)之间,则0 综上所述,IGWO算法的Markov链是遍历链. 文献[17]已经证明,若一个进化算法满足以下条件:1)对可行解空间中任意2点x1和x2,x2是x1由算法中各种算子可达的; 2)若种群序列Q1,Q2,…,QT是单调的,则此进化算法以概率1收敛于问题的全局最优解. 由于IGWO算法种群序列的Markov链是遍历链,条件1)显然是成立的. 由于IGWO算法中头狼引领、狼群互动和围捕行为的位置状态更新都体现出优秀解的保持策略,所以IGWO优化解序列是一个有限齐次Markov链,并且每次种群个体位置只有遇到更优解时才会更新. 因此,IGWO算法产生的子代Qk+1中的任意解都非劣于Qk,由此可得种群序列Q1,Q2,…,QT是单调的. 综上所述,IGWO算法以概率1收敛于问题的全局最优解. 为检验IGWO 算法的寻优能力,将本算法与SSA、BSA、SSO-C、LSO、DSA和标准GWO算法在同样的环境下进行仿真比较. 所使用电脑的详细设置:CPU为Intel(R)Pentium(R)CPUG2020;频率为2.90 GHz;内存为4.00 GB. 操作系统windows7,仿真软件为MATLAB2015b. 实验选取5个标准测试函数进行测试,如表1所示. 表1 标准测试函数 BSA算法中,c1=c2=1.5,a1=a2=1,FQ=10;SSO-C算法中,PF=0.65;LSO算法中成年狮的占比β=2%;DSA算法中,T1=3,T2=1 000,速度为1,A=5,M=3,e=4. 为保证测试的公平性,6种算法的种群数量均为100,最大迭代次数M=200,为避免单次运行的随机性带来的影响,各算法独立运行20次,取平均值和标准差. 5个测试函数分别在D=2、D=30和D=100这三种维度下进行仿真. 为验证IGWO算法的有效性,对各算法的寻优精度和收敛速度进行比较分析. 表2为7种算法对5个标准测试函数的寻优结果. 表2 7种算法的对比测试结果 由表2可知,在求解单峰f1、f2函数时,7种算法在D=2时均能找到精度较高的解,IGWO算法和LSO算法直接找到了最优解, DSA算法求解值精度相对较低;当维度增大到30或100时,IGWO算法和BSA算法依然能找到最优解,GWO算法和LSO算法随着求解维度的增大求解精度有所下降,SSA算法、DSA算法和SSO-C算法所得解误差较大,甚至找不到精度较高的解. 对于多峰f3、f4和f5函数,IGWO算法在几个函数上均得到了最优值,表明了该算法在低维和高维求解时都有很好的性能,适合求解多峰函数;GWO算法在D=2时能找到精度较高的解,但当求解维度增大时,求解性能有不同程度的下滑,甚至找不到精度较高的解,表明GWO算法不宜求解高维多峰函数;LSO算法在求解f5函数时,低维和高维情况下均取得了最优值,而在其他多峰函数的测试中表现一般,高维求解时所得结果偏差较大. DSA算法和SSO-C算法表现最差,求解精度相对较低,表明DSA算法、SSO-C算法存在一定缺陷,易陷入局部最优,不宜求解多峰函数. 此外,IGWO算法独立运行20次取得解的标准差均为0,表明该算法对不同维度的求解问题均具有很好的抗扰性. 图2为各算法在5个函数上的部分寻优曲线. 由图2可知,IGWO算法在单峰和多峰函数的寻优中,均具有较快的收敛速度,优于其他6种算法; GWO算法收敛速度较IGWO算法速度较慢,在f1、f2函数的寻优中,与IGWO算法相比收敛速度和收敛精度上都有很大的差距,但优于其他5种算法;BSA算法有较快的收敛速度,但差于GWO和IGWO;SSA算法在迭代前期收敛较慢,迭代后期收敛速度有所提升;LSO算法、DSA算法、SSO-C算法收敛速度较慢,在多峰函数的求解中很明显陷入了局部最优. (a)f1 (b)f2 (c)f3 (d)f4 (e)f5 采用文献[18]中的港口为研究对象,引入如下符号:B为泊位集合;l=1,2,3∈B,表示泊位;V为计划期内预计到港船舶集合;m=1,2,3,4…,表示船舶;O为每个泊位上船舶靠泊次序集合;n=1,2,3,4…,表示靠泊次序;Am为船舶到达港口的时刻;Blm为船舶开始靠泊位时的时刻;Clm为船舶在泊位上的待装时间;Wlm为船舶在泊位上的装卸时间. 船m的在港时间可以描述为:船舶开始靠泊时刻-到港时刻+泊位待装时间+装船时间. 即:Blm-Am+Clm+Wlm,所有泊位上船舶总的在港时间为 以船舶总的在港时间作为泊位调度问题的目标函数. 为得到优化目标的实际应用形式,令:xlmn={0,1},xlmn=1表示船舶m是在泊位l上的第n条被服务的船,xlmn=0,表示船舶m还在等待空闲泊位.ylmn表示在泊位l上第n条被服务的船到港时刻与同一泊位上第n-1条被服务的船离开时刻,如果ylmn<0,则让ylmn=0,即如果第n条被服务的船在第n-1条被服务的船离开之前到港,则它在第n-1条被服务的船离开时刻开始被服务. 假设在l泊位上有Pl条船被服务,Tl表示优化所选定的一段时间内泊位l变空闲的时刻,ms表示泊位l上第s条靠泊船的船号(s Wlm1+Wlm2+···+WlmPl+Tl-AmPl+ylm11+ylm22+ ···+ylmPlPl+Clm1+Clm2+···+ClmPl. 由所有船舶在港停泊时间相加,即可得到泊位l上所有船舶的在港停泊时间,将所有泊位的时间相加则为所有船舶总在港停泊时间. 目标函数是使所有在港船舶的总在港作业时间最短,即 约束条件: 1)每条船必须在某一泊位上被服务一次,即 2)每个泊位服务的船舶数应该等于总船舶数: 3)每条船必须在达到之后才能靠泊,即 (9) 在文献[19]的基础上,本文考虑7艘船的优化调度问题. 已知煤炭码头港口在2018年12月20日共有7艘船(A1、A2、A3、A4、A5、A6、A7)到港,到港时间分别为: 6:00、 8:00、 12:30、 17:30、18:00、 19:00、21:00; 港口有3个泊位可接待这些船舶:13号泊位12月21日23:00开始处于空闲;14号泊位12月20日20:12开始处于空闲;15号泊位12月21日16:36开始处于空闲. 按经验调度可根据船舶到港时间进行,安排1号、4号、7号船停靠13号泊位,2号、5号船停靠14号泊位,3号、6号船停靠15号泊位. 根据式(9)可得3个泊位总停时间为451.6 h. 现采用IGWO算法对该问题求解. 将第一条船到港的时间记为0:00时刻,则根据船舶在港口的时刻表可得表3、4. 表3 2018.12.20某煤炭码头船舶到港时间顺序表 表4 2018.12.20某煤炭码头船舶在港服务时间分布表 相应的13#、14#、15#泊位从第一条船到港至处于空闲的等待时间为41.0 、14.2、34.6 h. 采用IGWO算法求解,得到最佳靠泊方案为:(3、5、8、4、2、1、9、6、7),所有船舶在港停留总时间为385.3 h,较原来的451.6 h缩短了66.3 h. 可见利用IGWO算法求解能够得出相对较佳的调度方案,可实现泊位停靠最优化. 本文针对GWO算法存在的缺陷,提出一种改进灰狼算法(IGWO),经测试函数验证后应用到港口泊位调动中. 1)采用Sin混沌序列进行初始化,并引入头狼引领策略、合作竞争机制和自适应权值,增强了个体间的信息交流,提高了信息利用率,从而加快了算法的收敛速度. 2) IGWO算法在求解低维函数和高维函数时均能得到精度较高的解,且收敛速度明显快于GWO算法、LSO算法、DSA算法、BSA算法、SSO-C算法和SSA算法,说明该算法具有较快的收敛速度和较高的寻优精度. 3)在港口泊位调度中的应用,取得了满意的应用效果,结果表明,经过IGWO算法优化后,所有船舶停留总时间较优化前缩短了14.7%,大幅度缩短了船舶的在港时间,提高了生产效率,为实现船舶优化调度提供了有效方法.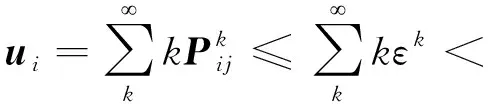
4 仿真测试
4.1 标准测试函数

4.2 参数设置
4.3 实验分析
5 IGWO算法在港口泊位调度中的应用
5.1 优化模型的建立
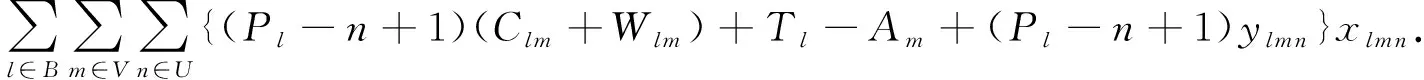
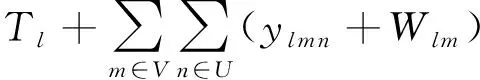
5.2 算例分析

6 结 论

