水泥稳定碎石材料孔隙特性研究

吕悦晶，刘 标，张 蕾，汤 文

(1.武汉科技大学 汽车与交通工程学院，武汉 430065； 2.交通运输部公路科学研究院，北京 100088)

水泥稳定碎石是一种具有强度高、整体性强等优点的半刚性材料，广泛作为公路工程的路面基层材料[1]. 水稳半刚性基层存在初始孔隙，初始孔隙经荷载与环境耦合作用导致孔隙结构发生变化从而形成孔隙裂纹，再经疲劳累积作用导致孔隙裂纹逐步发展使得路面基层出现开裂破坏，最后开裂的裂纹扩展至整个路面基层并延伸至路面顶层，形成反射裂缝，致使沥青路面损坏[2-5]. 荷载在水泥稳定碎石材料孔隙的发展、破坏这一过程中发挥着不可替代的作用，因此研究水泥稳定碎石材料中孔隙受荷载作用时孔隙结构的演化规律，非常有实际意义[6-8].

目前，不少学者采用CT技术与电镜技术获取材料内部的无损检测图像. 毛灵涛等[9]采用工业CT观测水泥稳定碎石材料孔隙发展、连通的全过程，把试件破坏分为弹性压缩、塑性变形和破坏扩容3个阶段，研究结论表明，裂缝不仅沿骨料边缘扩展，还会穿过骨料，文中研究虽能解释平面孔隙的变化过程，但缺少三维孔隙的研究；王一琪[10]采用X-CT技术结合VGStudio MAX 3.0软件，提取水稳材料孔隙参数，分析不同冻融循环条件对孔隙参数的作用，研究结论表明，改变冻融循环次数对孔隙参数影响很大，文中研究虽能解释冻融条件对孔隙参数的影响，但缺乏荷载作用对水稳材料孔隙的研究；孙亮等[11]结合扫描电镜技术与数字岩心技术，将孔隙连通域分为三级，研究结果表明，量化分级能有效区分材料孔隙特征，文中研究虽能量化区分连通孔隙，但对象是静态孔隙结构，缺乏力学变化作用下孔隙连通性的变化研究；Wang Y等[12]采用X-CT技术，研究养护时间、水泥用量对水稳材料孔隙结构的影响，研究结果表明，水泥掺量的增加与养护时间的延长会导致平均孔隙直径减小，文中研究虽能解释水泥掺量与养护时间对平均孔隙直径的关系，但缺乏平均孔隙直径与荷载的关系. 本文基于CT技术或电镜技术无损检测材料的特点，针对上述研究的不足，运用CT技术与获取不同荷载下水稳材料的CT图像，从细观尺度研究材料的孔隙结构.

在其他研究领域，不少学者基于细观尺度对材料的孔隙结构进一步研究，将孔隙结构演化为孔隙三网络结构[13-16]. 上述文献在其他研究领域，采用光学成像技术、原理编程技术，X-ray扫描技术建立孔隙网络模型，根据孔隙网络模型对材料孔隙结构深入分析，取得很好的效果，但孔隙网络模型在道路工程领域的运用则很少. 因光学成像技术或编程技术对设备和电脑要求高且不易实现，而X-ray与pore3D软件结合技术则缺乏pore3D平台，所以本文结合现有条件，将CT扫描与avizo软件结合，运用数值图像处理技术和中轴线原理建立水稳材料的孔隙网络结构，深入研究分级荷载下孔隙结构的体积、喉道、配位数等参数变化规律.

1 试验设计

1.1 材料设计

集料为石灰岩，水泥为32.5普通硅酸盐水泥，按幂函数间断级配设计4.75 mm通过率分别为30% 和45% 的2种级配，级配编号为N1和N2，每组级配6个试件，其水泥稳定碎石配合比设计构成见表1，石灰岩与水泥的相关参数分见表2、表3. 根据击实试验和抗压强度试验确定最佳含水率和水泥掺量.

表1 水泥稳定碎石试验配合比设计

表2 石灰岩相关参数

表3 水泥相关参数

1.2 试件成型

根据《公路工程无机结合料稳定材料试验规程》(JTG E51．2009)中水稳混合料试件制作方法，采用直径150 mm、高150 mm圆柱型试模，将预先配比的水稳碎石材料拌和、装模，最后采用静力压实成型试件. 静压成型试件后，在养生温度为20 ℃、湿度为95%的环境下，养生7天龄期，最后一天浸水，测试龄期也为7天. 强度满足要求后，钻取直径75 mm、高150 mm的芯样.

1.3 加载及CT扫描

试验采用工业CT扫描机同步加载试验装置，工业CT扫描机的理论最大密度分辨率0.2%，最大电压320 kV，扫描方式为锥束射线，单次扫描区域为扇形区域，加载方式为位移加载控制模式，加载速率为1 mm/min. 根据预加载试验，试件破坏峰值在[60 kN，70 kN]，大部分试件在荷载级为60 kN时已经出现明显的裂纹，且为获取水稳材料不同损伤程度的CT图像，将N1、N2级配荷载级位都设定为0 kN、20 kN、40 kN、60 kN. 结合CT扫描时外界环境干扰因素和试件损伤破坏程度的实际情况，先从两组级配中选出具有较好代表性的试件，后为避免人为因素干扰，再从两组级配的代表性试件中各随机选取一个试件作为研究对象，最后根据试件断面扫描效果，选取两个试件的同一区域400张CT图像，图像大小为1024×1024pix，CT图像分辨率为15 μm.

2 建立三维模型

avizo软件以多层图像连续贴合的方式导入400张CT图像，为保证后续建立的模型与实际试件尺寸一致，需将CT图像导入avizo后，设定计算单位，单位设定为微米(μm)，单体素为100.0 μm *100.0 μm *100.0 μm. CT图像经数值图像处理技术的中值滤波、锐化技术初步处理后，对图像体素的红、绿、蓝三基色合成与渲染，生成芯样三维模型如图1(d)所示.

经图像二值化，孔隙分割算法深度处理CT图像，凸显孔隙目标轮廓，求解孔隙信息，并运用形态学开、闭运算精细处理孔隙，效果如图1(e)所示[17]. 将提取的高精度CT图像的孔隙体素的三基色合成与渲染生成孔隙三维模型，如图1(f)所示，该孔隙三维模型中既有断层孔隙体素信息，也有三维孔隙体素信息.

(a)芯样 (b)图像原图 (c)中值滤波图 (d)芯样三维模型 (e)孔隙分割图 (f)孔隙三维模型

3 孔隙三维模型的断面孔隙率与三维孔隙率特性分析

图1(f)的孔隙三维模型能直观反映孔隙空间结构、孔隙分布状态，还能定性反映孔隙空间结构的复杂性，但缺乏孔隙信息的定量表征. 为定量表征材料宏观破坏和细观孔隙率变化规律，将上述模型的断面孔隙信息与三维孔隙信息以断面孔隙率和三维孔隙率形式量化，孔隙率量化计算原理[17]为

(1)

式中：若P表示断面孔隙率时，Vvoxel表示断面孔隙体素，VTOTAL表示截面总体素；若P表示三维孔隙率时，Vvoxel表示孔隙三维模型中整体孔隙体素，VTOTAL表示芯样的三维模型总体素.

3.1 断面孔隙率特性

不同荷载级对水稳材料的破坏损伤程度不同，损伤破坏过程中细观孔隙率变化过程也会有所差别，因此研究分级荷载与细观孔隙率发展规律有利于分析水泥稳定碎石材料的宏观破坏原因，基于此分别建立0 kN、20 kN、40 kN、60 kN各级荷载的孔隙三维模型，并采用式(1)求取连续断层的断面孔隙率. 将400张CT图像自上而下沿断面层位编号即断面层位数，以断面层位数为x轴，断面孔隙率为y轴，但为直观表示试件区域，x轴以上部、中部、下部显示，如图2所示.

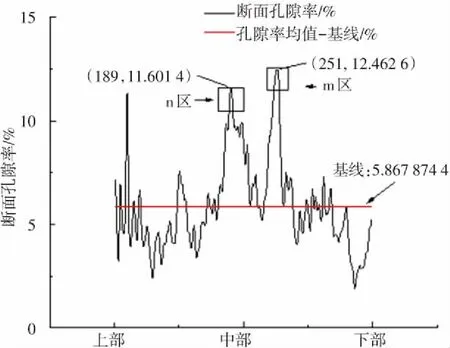
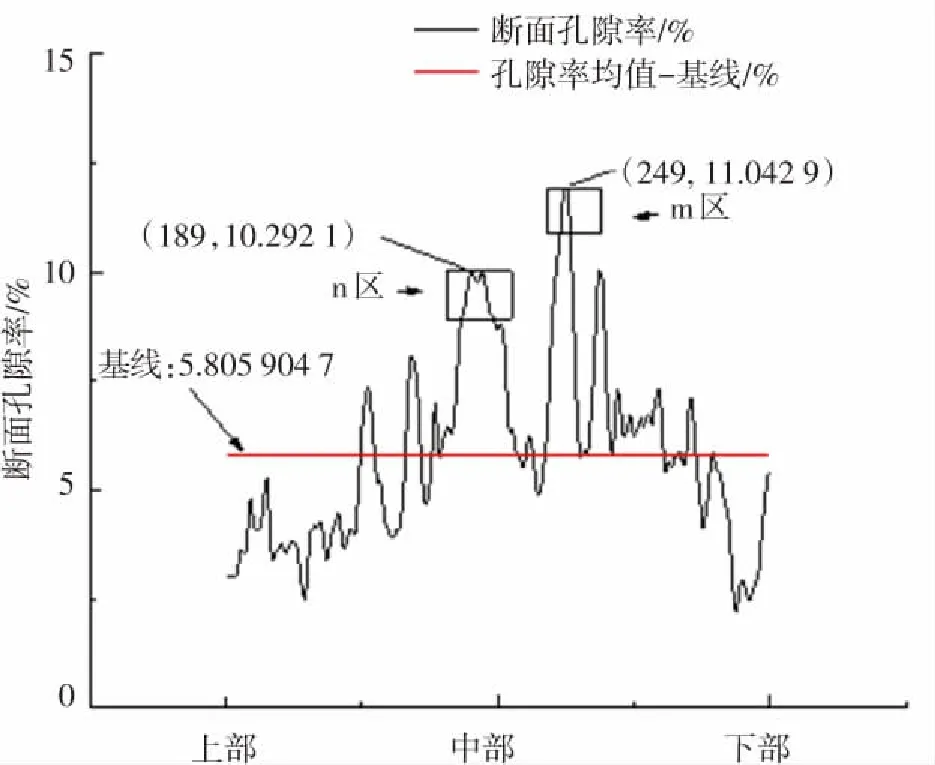
由图2知，各荷载断面孔隙率图形大致相同，都呈现两端小、中间大的分布趋势，且在一定断层区域内断面孔隙率有先增大后减小然后又增大的趋势，还有波形图的最大峰值与第二峰值都集中在中部，红色基线之上都有数个明显的波峰. 图中红色基线为断面孔隙率均值，均值能直观反映水稳材料在不同破坏程度时，内部孔隙结构平均变化规律，且将基线与断面孔隙率组合绘图，表达孔隙信息更丰富. 各荷载波形图也有不同之处，0 kN和20 kN图形基本上保持一致，40 kN、60 kN变化较大；40 kN 靠近上部出现突变值，该突变值发生的原因是40 kN的初始CT图像受环境和机器干扰较大，该值已失真，但因该区域为研究区域，为保证数据真实性没有将该区域舍弃；20 kN基线值小于0 kN基线值，40 kN基线值大于0 kN基线值，且60 kN基线值最大，0 kN到60 kN基线值变化趋势为先减小后增大；60 kN波形图对比其他波形图，其断面孔隙率最大值与最小值差值跨度最大.

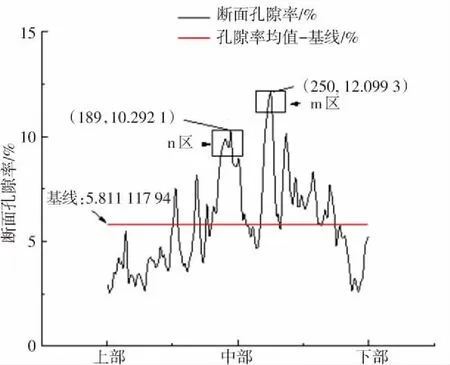
(a)0 kN波形图

(c)40 kN波形图

(b)20 kN波形图

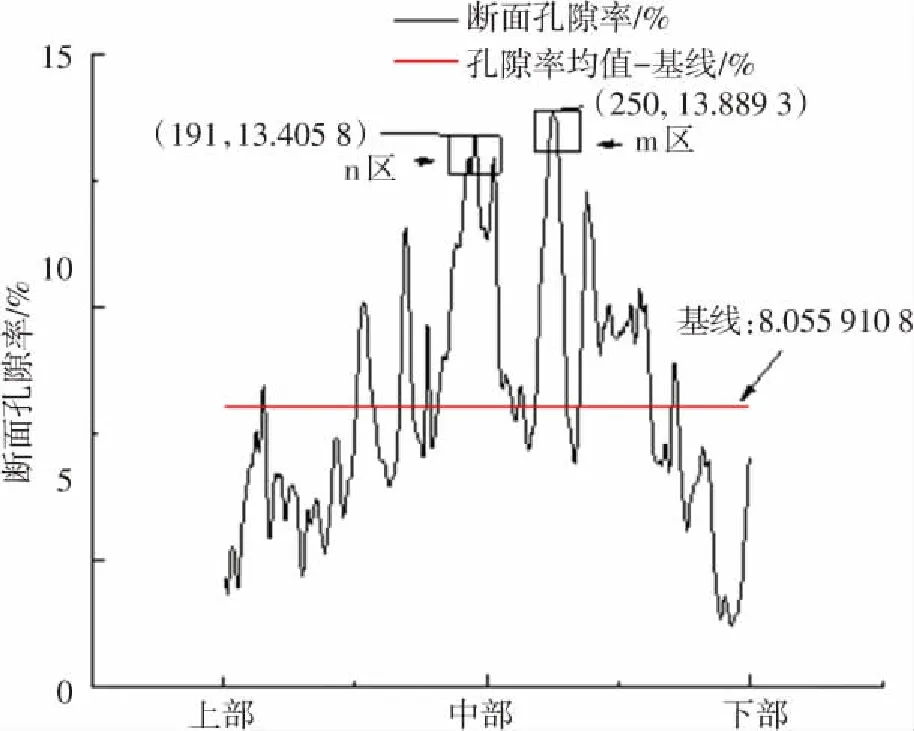
(d)60 kN波形图

定义最高峰值区域为m区，第二峰值区域为n区，这两区域为断面孔隙率极大值区域，能有效代表断面孔隙率变化规律，因此选取m区、n区来说明细观孔隙变化与材料宏观破坏的关系. 图2的4幅图中m区形状类似，都为凸起尖锐状，但峰值对应层位数略有变化，集中变化在249-251层位，最高峰值从0 kN的12.10%扩展到60 kN的13.89%；n区形状变化较大，20 kN的n区与0 kN对比，由尖锐变为平滑；20 kN到40 kN、60 kN，n区由20 kN的平滑演变为40 kN的尖锐单波峰和60 kN的多峰、多谷；峰值层位变化也较大，变化集中在180-191层位，层位跨度为11；而且60 kN的第二峰值由10.29%突变为13.41%，断面孔隙率波形图变化十分明显. 其他不少区域的波形、峰值、峰值层位数也如m、n区一样有较剧烈变化，这说明荷载作用导致孔隙细观结构改变剧烈.

分析上述原因，0 kN到20 kN，宏观荷载初步施加，材料内部孔隙被压实，断面孔隙收缩，断面孔隙率从尖锐过渡为平滑，20 kN增大至40 kN、60 kN，内部孔隙从压实状态变为细小孔隙积累状态最后突变为孔隙裂纹扩展状态，断面孔隙率则从平滑状态变为单波峰以及多波峰状态；这表明材料在宏观荷载逐级破坏过程中，断面孔隙细观结构会出现收缩聚拢然后细小孔隙积累最后孔隙连通、扩展等剧烈结构变化，孔隙细观结构剧烈变化促使材料内部结构破坏，进而材料出现宏观破坏，因此孔隙细观结构剧烈变化与材料宏观破坏有着必然联系.

3.2 三维孔隙率特性

断面孔隙率将细观孔隙率与宏观荷载相联系，但缺少三维孔隙率随荷载变化关系，因此运用上述已建立的孔隙三维模型，求取三维孔隙率. 以荷载级为x轴，相应荷载级的三维孔隙率为y轴，建立两组级配的荷载与三维孔隙率关系趋势图，如图3所示. 由图3知三维孔隙率随荷载先变小后增大，60 kN增至最大，图形变化规律与试验中孔隙率随荷载变化规律相似，说明采用孔隙体素与芯样体素比值表示孔隙率的方法能实际表征孔隙随荷载变化规律. 将0 kN的三维孔隙率与试件实际值比较，误差很小，说明该模型能重现试件. 图形变化规律继续研究，发现在荷载逐级增加过程中，三维孔隙率先减小后增加的规律与断面孔隙率最大峰值、第二峰值以及基线值的变化趋势一致，进一步表明细观孔隙变化与材料宏观破坏有必然联系.

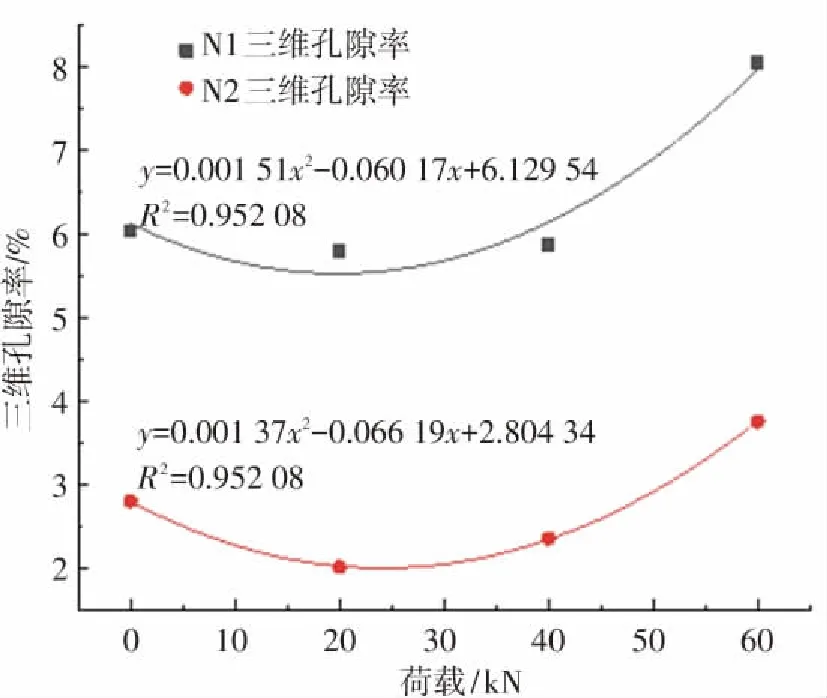
图3 荷载与三维孔隙率关系趋势图

4 孔隙三维网络结构及参数特性

断面孔隙率与三维孔隙率是以孔隙率量化的形式表征宏观荷载作用下细观孔隙与材料宏观联系，但尚不足表达材料内部孔隙空间结构如何演化. 本文将孔隙三维模型简化转换成孔隙三维网络结构，然后提取该网络结构的孔隙相关信息，再将孔隙信息与荷载级组合分析，进而探究材料内部孔隙空间结构变化过程.

4.1 孔隙三维网络结构

孔隙三维网络结构是运用球体、柱体等规则形状描述复杂孔隙空间的一种方法，主要由孔隙和喉道两部分构成[18]. 孔隙三维网络结构中孔隙表示水泥稳定碎石材料中较大的孔隙空间，喉道表示连接相邻孔隙的细长空间即孔隙与孔隙的裂隙，简称为孔间隙. 孔隙三维网络结构采用中轴线法构建，即孔隙空间中心位置的体素集合构成球度不一的球体，然后构建成孔隙三维网络结构.

以图4说明转换过程，图4(a)中蓝色部分为连通孔隙，蓝色连通孔隙基于等效替换原理转换为球体，实际孔隙越大，相对应替换球体越大；灰色部分为喉道，喉道简化一般以图4(b)[11]的孔隙三种连通形式简化替换，即相邻孔隙之间若存在着三种连通级别的一种，则将实际孔间隙替换成相应的喉道.

等效替换原理[19]为

(2)

式中：Dcq为等效孔隙直径，Vpore为孔隙体积.

将图1(f)的孔隙三维模型运用上述简化替换原理在软件中快速生成孔隙三维网络结构，如图5所示，图中红色球体为孔隙，黄色柱体为喉道即连接相邻孔隙的孔间隙，借助孔隙三维网络结构能直观反映材料孔隙空间特性.

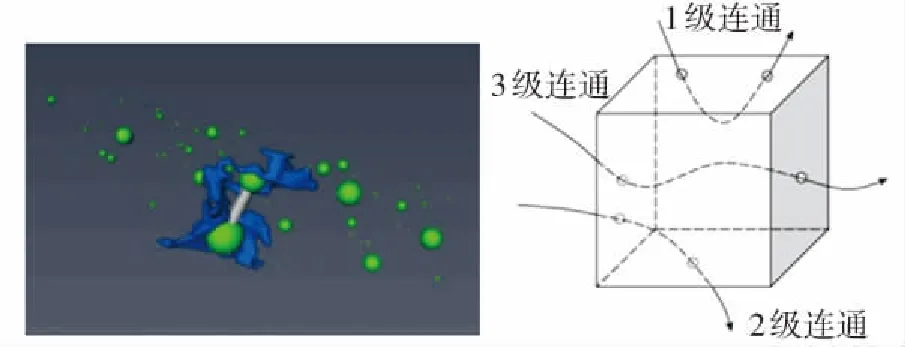
(a)孔隙替换图 (b)孔隙连通级图

图5 孔隙三维网络结构

4.2 孔隙三维网络结构参数特性

将各级荷载的孔隙三维模型都转换为孔隙三维网络结构，提取各级荷载的孔隙三维网络结构的孔隙配位数、孔隙体积、喉道长度等参数信息，并对参数信息进一步分析，探究孔隙三维网络结构中孔隙空间结构变化进而演化材料损伤破坏过程. 其中，孔隙配位数是指孔隙连通其他孔隙的喉道数量，喉道长度指连通孔隙的孔间隙长度.

4.2.1 孔隙配位数特性

表4列出各级荷载的孔隙数量、喉道数量、孔隙配位数，还有孔隙配位数的最大值、最小值、均值. 表中孔隙配位数指各级荷载下所有孔隙连通其他孔隙的喉道总数量，配位数最大值表示单个孔隙最多连通其他孔隙的喉道数量，最小值表示单个孔隙最少连通其他孔隙的喉道数量，配位数均值指单个孔隙连通其他孔隙的平均喉道数量，是由孔隙配位数与孔隙数量比值得到. 由孔隙配位数均值计算方式可知，配位数均值可表征材料孔隙空间连通程度，均值越大说明孔隙空间连通越强，进而推断出孔隙空间结构中连通孔隙比例越大；反之，孔隙空间连通越差，则孔隙空间结构连通孔隙比例越小；孔隙配位数的最大值与最小值则反映出孔隙结构的空间局部孔隙连通的强与弱.

表4中0 kN、20 kN、40 kN孔隙配位数均值都小于0.45，均值依次为0.4470、0.4367、0.4306，均值之间虽较接近，但呈现减小的趋势，但60 kN孔隙配位数均值则突变为0.5050；0 kN、20 kN、40 kN配位数最大值依次为9、9、8，与配位数均值变化趋势一样，呈现减小趋势，但60 kN配位数最大值则由8、9突变为11；配位数最大值变化趋势与配位数均值变化趋势具有一致性，这说明局部孔隙连通性程度与整体孔隙连通性程度保持一致，进一步说明局部孔隙空间结构变化规律与整体孔隙空间结构变化规律保持一致. 无论材料是否受到荷载作用或者材料在荷载作用下是否破坏，都有孔隙配位数最小值为0的情况. 将0 kN、20 kN、40 kN、60 kN的配位数其他数值绘制成柱状图，如图6所示，图中配位数数值在1-3区域的百分数比例60 kN明显小于0 kN、20 kN、40 kN，但配位数数值大于4后的百分数比例，60 kN明显大于0 kN、20 kN、40 kN.

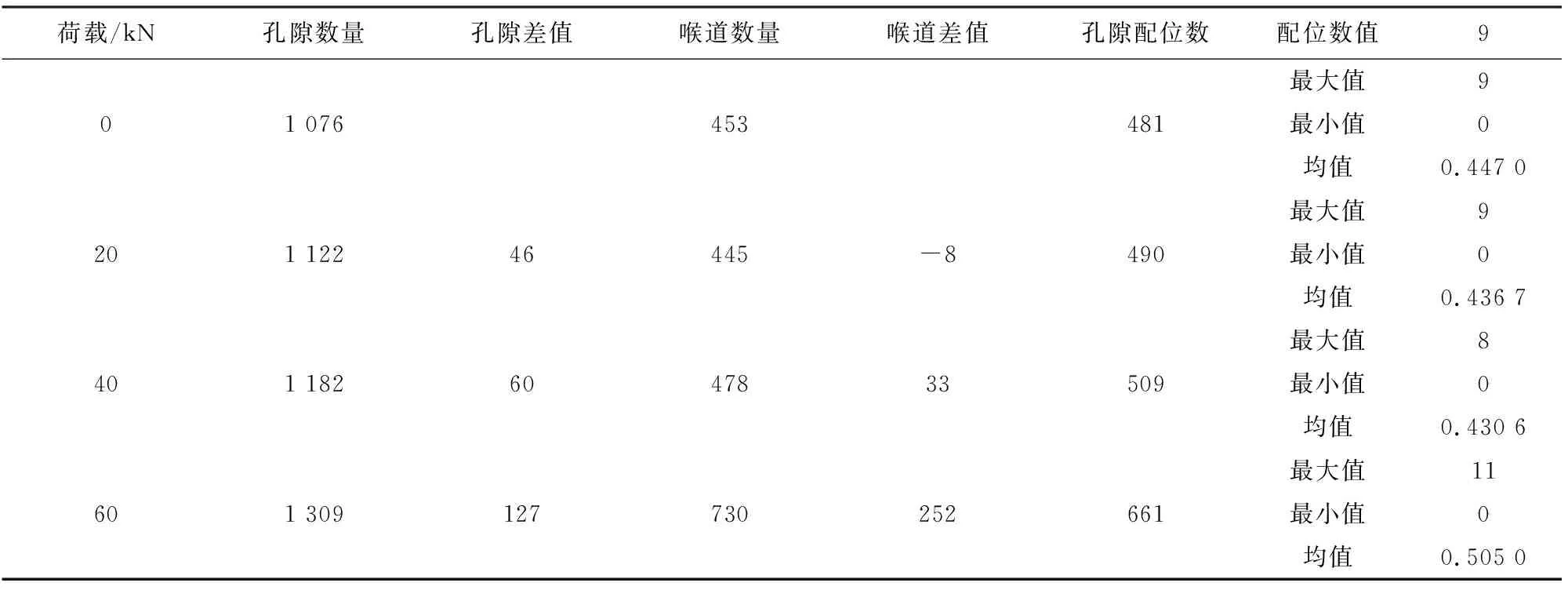
表4 孔隙三维网络结构参数

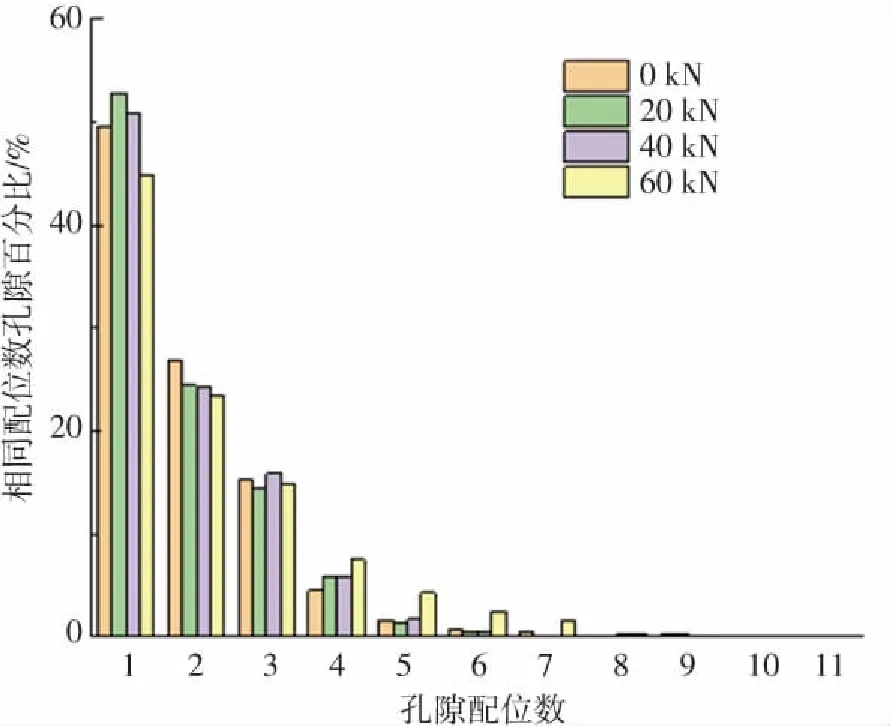
图6 荷载-孔隙配位数百分比

上述原因分析，水泥稳定碎石材料具有初始孔隙空间连通性，各级荷载下孔隙空间连通程度不一致，局部空间最大连通程度也不一致，但都存在局部空间不连通；随荷载逐级增加，材料孔隙空间连通程度先减小，但在材料破坏时，材料孔隙空间连通程度明显增强，孔隙空间结构中连通孔隙比例显著增加，导致配位数最大值和配位数数值大于4之后都出现明显的突变；这说明宏观荷载作用过程中，孔隙空间结构会有部分孔隙发生相互连通、连接的演变过程，此过程导致孔隙空间结构的连通孔隙比例会显著增加，促使材料破坏.

4.2.2 孔隙体积特性

孔隙体积特性有利于研究孔隙空间结构中孔隙大小演变过程，探究孔隙扩展机理，将孔隙体积随荷载变化规律以柱状图百分数形式表示，如图7所示.

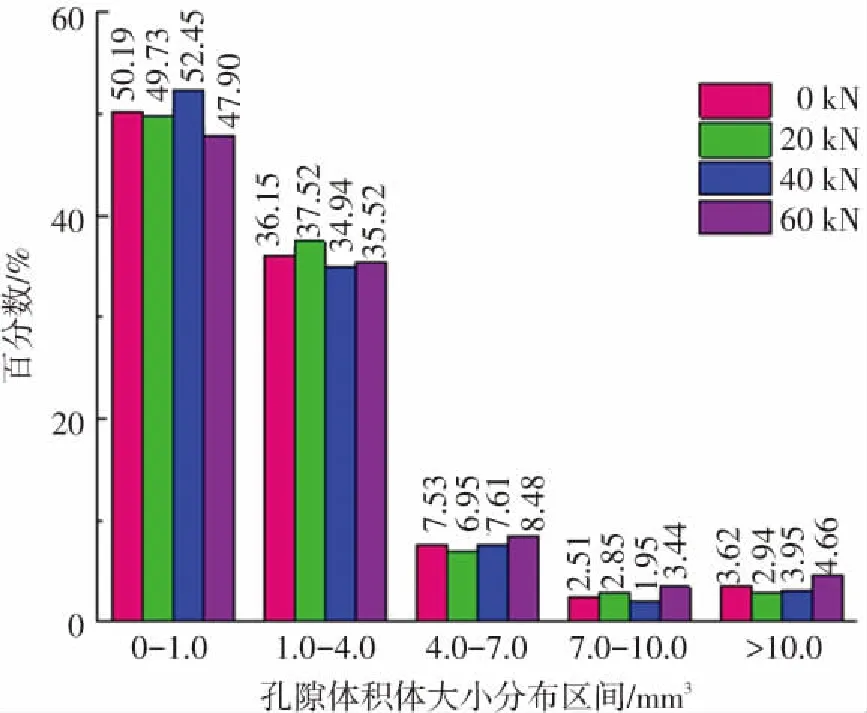
图7 孔隙体积区间分布图

图7中各级荷载的体积尺寸分布在0～1.0 mm3和1.0～4.0 mm3区域的孔隙百分数比例之和超过80%，因此以4.0 mm3为标准将孔隙分为小于4.0 mm3的小孔隙和大于4.0 mm3的大孔隙；60 kN的小孔隙的百分数之和小于其他荷载级，但20 kN、40 kN的小孔隙的百分数之和对比0 kN略有增加；大于4.0 mm3的大孔隙，60 kN的比例分数明显大于其他荷载的比例分数，且20 kN、40 kN的比例百分数对比0 kN、60 kN具有明显减小趋势.

图7图形变化规律分析，无论材料是否受到外界荷载作用，材料内部细小孔隙占比都超过80%，但因逐级荷载作用使得材料状态发生改变，特别是在荷载破坏前后，孔隙空间结构的孔隙体积发生明显变化；在材料破坏前，孔隙空间结构是以细小孔隙产生为主，但材料破坏后，孔隙空间结构则是以细小孔隙连通、扩展成大孔隙为主.

4.2.3 喉道特性

不同荷载的喉道变化规律可以反映荷载作用时材料的孔隙空间结构中孔隙裂纹演变过程，但表4的喉道差值信息只能简单反映出喉道数量具有先减小后急剧增加的规律，喉道长度实际如何变化还需进一步研究.

以各级荷载的喉道数量为x轴，喉道长度为y轴，绘制荷载喉道长度分布图，如图8所示.

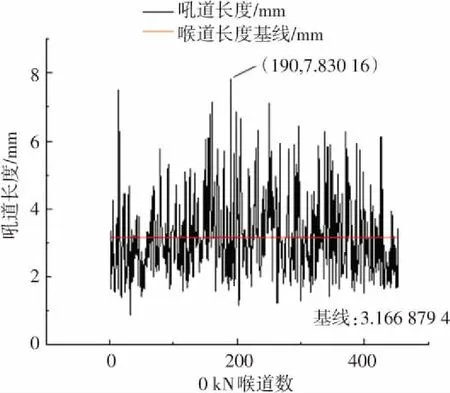
(a)0 kN喉道长度分布图

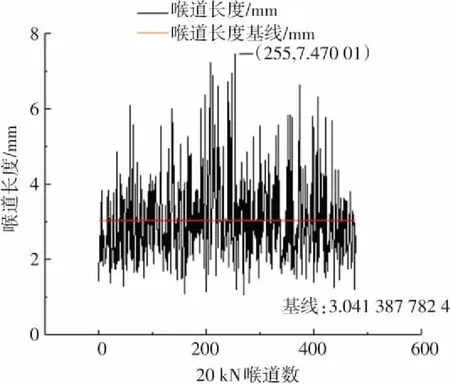
(c)40 kN喉道长度分布图

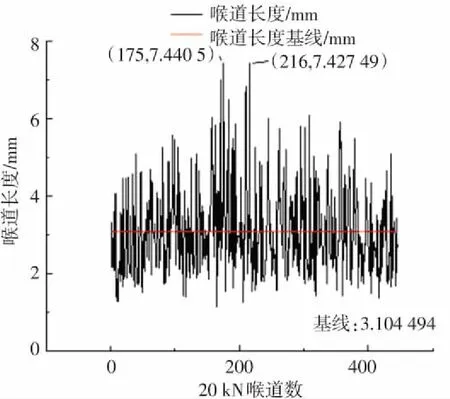
(b)20 kN喉道长度分布图

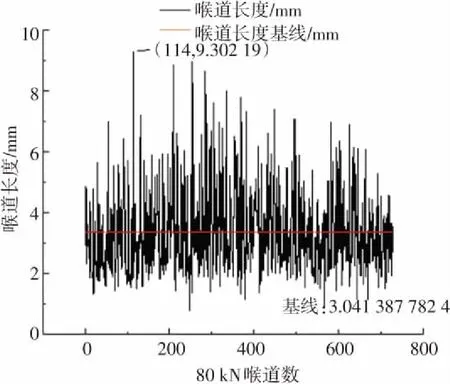
(d)60 kN喉道长度分布图

图8中0 kN、20 kN、40 kN喉道最大值分别为7.8 mm、7.4 mm、7.5 mm，都在7.5 mm左右，但60 kN最大值为9.3 mm，喉道长度扩大近2 mm；20 kN、40 kN对比0 kN，不仅喉道长度最大值减小而且红色基线所表征的喉道长度均值也减小，60 kN对比0 kN、20 kN、40 kN不仅最大值突变至最大，基线值也增至最大，喉道长度最大值与喉道长度均值变化保持一致.

上述原因分析，20 kN、40 kN时荷载施压使得芯样内部细集料逐渐被压实，导致材料喉道即细小孔间隙被填充，孔隙空间结构被压紧聚拢，材料中孔隙裂纹不仅没发生反而出现原有孔隙收缩，因此孔隙空间结构的孔隙裂纹呈现负向演变；但在60 kN时，荷载作用导致孔隙将周边集料撑裂形成孔隙裂纹，且孔隙空间结构会继续扩展延伸，导致孔隙裂纹呈现正向演变，孔隙裂纹正向演变促使材料加剧破坏，材料的加剧破坏又促使孔隙裂纹进一步正向演变，因此导致材料破坏时孔隙裂纹演变会突变为最大.

上述对孔隙配位数、孔隙体积、喉道长度特性研究可知，孔隙空间结构中配位数、孔隙体积、喉道长度等参数的剧烈变化，表明在荷载作用下孔隙空间结构改变剧烈，孔隙空间结构的剧烈变化促使材料内部结构改变，进而材料宏观破坏，这对揭示水泥稳定碎石材料在荷载受力时孔隙破坏机理具有重要理论意义.

5 结 论

1)孔隙三维模型以及转换为孔隙三维网络结构的方式，能演变荷载作用下孔隙细观结构和孔隙空间结构变过过程，孔隙结构剧烈变化促使材料内部结构改变，外部荷载作用与内部结构改变导致材料宏观破坏，因此材料宏观破坏与孔隙结构变化有本质联系.

2)孔隙三维模型中量化断面孔隙与三维孔隙的方式能表征水稳材料的孔隙细观结构变化；m、n区的波形较剧烈变化，m、n区峰值从12.10%、10.29%分别扩展到13.89%、 13.41%，峰值层位跨度为3、11个层位，三维孔隙率先减小后增大的规律，都从细观角度表明逐级荷载改变孔隙结构.

3)孔隙三维网络模型中配位数最大值由8、9突变为11，配位数均值由小于0.45突变为大于0.5，喉道长度由7.5 mm左右增加到9.3 mm，孔隙体积有孔隙连通、扩展过程，说明荷载作用导致材料孔隙空间结构剧烈变化.