一种从离散模拟到连续介质弹性模拟的过渡方法1)

宓思恩 刘小明 魏悦广，2)

* (中国科学院力学研究所非线性力学国家重点实验室，北京 100190)

† (中国科学院大学工程科学学院，北京 100049)

** (北京大学工学院力学与工程科学系，北京 100871)

引言

先进结构材料基于微纳米结构设计，其宏观力学性能依赖于微纳米结构，具有跨尺度力学特征[1-4].对其跨尺度力学性能的准确模拟，需要采用从微观的离散MD (molecular dynamics)模拟到宏观的连续介质表征.然而从离散体系到连续介质体系的过渡是面临的挑战性科学和技术难题.原子模拟理论和方法的发展使得材料在纳米尺度下的力学行为得到了充分的研究[5-9].如何将原子模拟方法与基于连续介质力学理论的表征相关联，把握先进材料的跨尺度力学行为，有效地建立先进材料的跨尺度力学理论，从而有效表征其在不同尺度下的力学性能成为一个重要的研究方向[10-13].其中，如何在离散原子体系中计算针对连续介质定义的力学变量也是亟需解决的一个重要的科学技术问题.由于在原子模拟中(如MD)，模型由离散的原子构成，体系中对于应力和应变等连续介质力学理论框架下的力学变量并没有统一的定义.许多研究都试图在原子模拟中定义与传统连续介质力学等效的应力和应变，由于原子结构及原子运动的多样性和离散特征，基于该过程给出的应力和应变的定义是难以直接与连续介质理论的应力-应变定义形成有效过渡的，在过渡区不可避免地引起非平衡“鬼力”.为此，本文试图建立一种从离散模拟(MD) 到连续介质弹性FEA (finite element analysis)的过渡方法.在介绍这一过渡方法之前，下面首先简要回顾一下若干MD 模拟研究中相关应力和应变概念的定义和原理.

在离散体系MD 方法中，人们也曾对应力和应变的概念进行过定义和相关研究，例如，Irving 和Kirkwood[14]在流体力学方程的推导中，根据统计力学原理定义了位力应力(virial stress)的概念，其中连续流体中的每一微小部分都被视为由N个微粒所组成的系统，应力则被描述为该系统所受的面力，其中包含动能项与微粒间的作用力项.这种方法在计算过程中引入了适当的时间和空间量的平均，并且在计算微粒间的相互作用力时，为了将统计力学与流体力学运动方程相联系，只考虑通过微粒中心的作用力项，因此在计算微粒间作用力项时，只计算了微粒的正应力.Hardy 等[15-16]注意到在Irving 和Kirkwood[14]的工作中，离散系统中守恒定律的准确性依赖于整体的平均，研究过程中引入了无穷级数和狄拉克δ函数，需要通过近似求解确定.Hardy 使用了一种局域函数来代替狄拉克δ函数，以克服Irving 和Kirkwood 的工作在数学上的复杂性.这种局域函数代表对一个空间原子的运动产生显著影响的所有原子所占有体积的特征尺度，Hardy 证明了这种局域函数的取值范围可以任意选择，通过取极限，获得稳定的位力应力值.Zimmerman 等[17]将Hardy 提出的计算方法与局部平均的位力应力作对比，显示Hardy 的方法在绝大多数情况下的精确性更优于局部平均的位力应力.在这两种表达式中，选取不同特征体积时计算得到的应力值不同，但其波动的幅度都可以通过适当扩大参与计算的特征体积，或引入适当的时间平均降到最低，以此得到一个稳定值.Tsai[18]提出了另一种计算应力的方法，该方法考虑了通过特定边界的力和动量通量，来计算边界所包含部分的应力.通过边界的合力的法向分量计算体内的正应力，边界面内的切向分量计算剪应力.Lutsko[19]进一步发展了Irving 和Kirkwood[14]的研究工作，通过局部的动量平衡方程和体积平均推导出应力张量.Zhou[20]在其理论中指出，传统的Cauchy 应力应该与原子的速度无关，只有分子间作用力部分才能真正对应于传统Cauchy 应力.位力应力的动能项依赖于原子的质量和速度，会违背动量守恒，且不具备明确的物理意义.Liu 和Qu[21]则从柯西应力的原始定义出发，论证了在经过合适的时间平均后，基本的拉格朗日原子应力与柯西应力等效，进一步提出了不含原子速度项的拉格朗日应力和欧拉应力，并证明经典的位力应力实际上对应欧拉位力应力.Falk 和Langer[22]在研究材料不可逆的剪切变形时，将局部的应变定义为一定范围内，邻近原子相对于中心原子的实际位移与发生均匀变形时的位移的均方差的最小值.Shimizu 等[23]在测量局部弹性应变时引用了其中均匀应变的计算.这是通过局部变形矩阵计算的拉格朗日应变，本质上反应原子与其邻近原子间的相对运动.虽然应变计算的形式简单，但是Gullett 等[24]指出，其中刚体的转动部分可能产生虚构的剪应变，导致计算错误.他们同时在文中介绍了变形梯度的计算，并与传统的连续变形梯度进行对比.同时，为了区分最邻近原子与稍远的原子的不同贡献，在变形梯度计算时引入了权函数.为了建立材料的原子运动离散体系与连续介质体系的应力和应变概念的关联，Mott 等[25]通过考虑原子结构特征给出了一种定义变形梯度的几何方法，以此获得对应变的定义.

由于原子的位置坐标本质上是离散的，计算所得的原子尺度的应力与应变值也是离散的，同时，以上所有的计算方法都需要选取一个合适范围来确定计算所包含的邻近原子(选取截断半径)，该范围的确定在一定程度上是任意的，其明显地对计算结果产生影响.在应力计算时采用的局域函数，以及计算变形梯度时的权函数也是通过不精确地拟合原子相互作用与原子间距离的关系所得，都会使计算结果受到人为因素的影响.因此，通过传统离散体系MD 模拟计算的应力与应变与连续介质力学框架下定义应力与应变之间存在一定的差异.

本文针对晶体材料的微观周期性结构特征，提出一种协同考虑材料原子结构、运动、模拟以及连续介质有限元分析的耦合计算方法，即MD-FEA 方法，将原子模拟结果直接转变为已知有限元节点位移的应力应变场的后处理问题，避免了在后处理过程中仍需选取截断半径的问题.该方法的显著优点体现在:既直接将原子运动离散体系转化为连续介质体系的力学场计算，又避免了传统原子模拟方法在后处理过程中由于选择截断半径而引起的误差.对于许多具有周期性晶格排布的材料(如FCC，BCC和HCP 等)，将基本原子结构选为连续介质有限单元十分容易，同时以原子位移作为单元结点位移，计算有限单元内的力学场也十分方便.因此，本文建立了一种结合了分子动力学与有限元分析的计算方法(MD-FEA)，针对典型FCC 晶体材料结构的力学问题(如，Al/Ni 双材料纳米杆的拉伸与纳米压痕)，开展新方法与MD 方法的比对研究，以验证新方法的有效性.

1 MD-FEA 方法

由于晶体材料中原子的排布具有周期性(如FCC，BCC 和HCP 等)，有利于将整个晶体材料的原子模型分割为有规律的单元体，进而整个模型的力学行为便可以运用有限元分析，通过各个单元的变形进行描述.以图1 中的面心立方晶体为例，分子动力学模型中的原子可以分割成若干有限元中的六面体单元，每个MD 模型中原子都可以视为单元中的节点.因此，每个FEA 六面体单元包含14 个节点，8 个位于六面体的顶点，6 个位于六面体的面心.每个顶点的原子同属于8 个单元，面心的原子同属于2 个单元.因此，通过MD 模拟得到每个原子的位移即为对应单元的节点位移，六面体单元的应变场可以通过属于该单元的14 个节点的位移进行插值计算.与传统FEA 方法不同的是，这种方法不需要计算模型的刚度矩阵，每个节点的位移都是通过MD 模拟获得的.

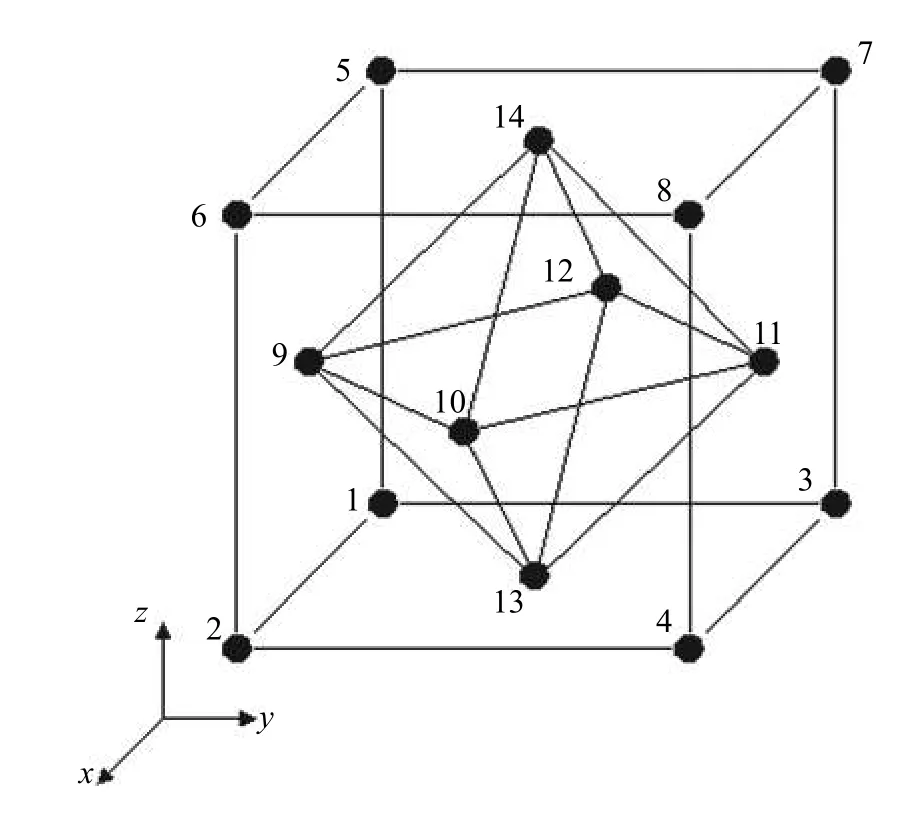
图1 14 节点单元示意图Fig.1 Schematic diagram of a 14-node element

1.1 MD 模拟的相关基本关系

求解原子的牛顿运动基本方程为

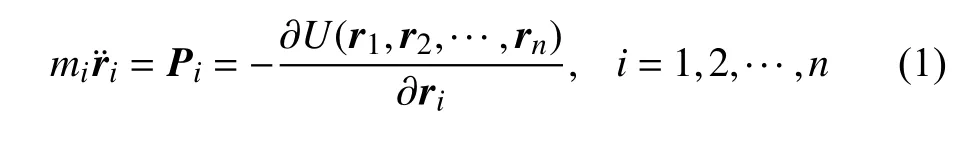
其中ri，mi，Pi分别为原子i的位置、质量和其受到的作用力，U为n个原子所组成的系统的总势能，由系统中每个原子的作用势求和得到.对晶体结构金属材料，常用的两种原子作用势为:Lennard-Jones(L-J)作用势和镶嵌原子势(EAM 势).

对于Lennard-Jones 作用势，单个原子的作用势Ei为

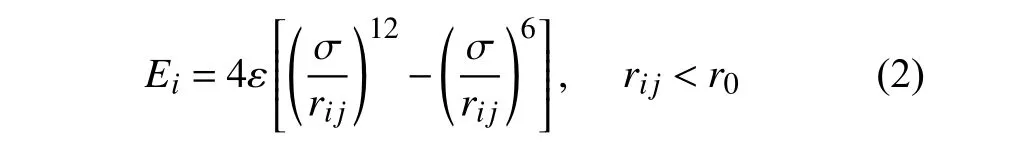
其中rij为原子i与j之间的距离，ε，σ和r0分别为两个原子的结合能，平衡距离和截断距离.

对于EAM 原子作用势[17-18]

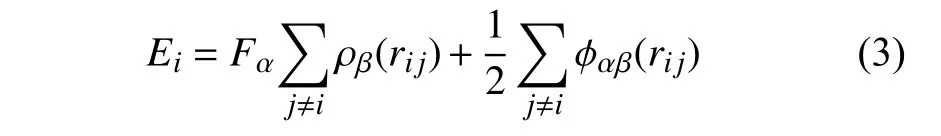
其中Ei是原子i的总势能，α和β分别为原子i和j的类别，F代表原子的镶嵌能，是该原子电子密度ρ的函数，rij是原子i和j之间距离，φ为对势.

1.2 FEA 相关基本关系

对于一个由面心立方晶体构成的14 个原子的结构，转换成有限元的单元结构即为由14 节点构成的空间六面体单元，其结构如图1 所示.常采用的等参元的位移场可以描述为

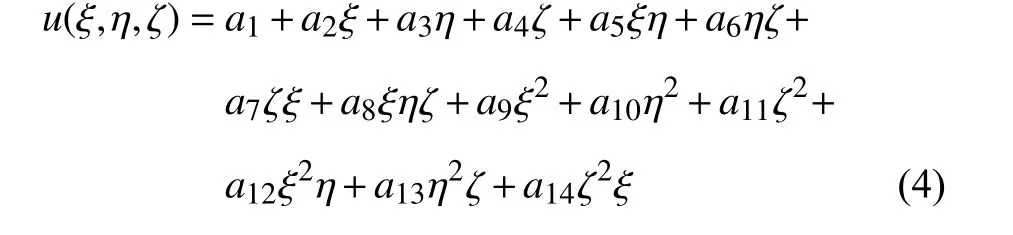
其中，- 1 ≤ξ，η，ζ ≤1 为等参元的坐标分量.

由此可以确定单元的形函数N为

因此单元内一点处的应变分量为

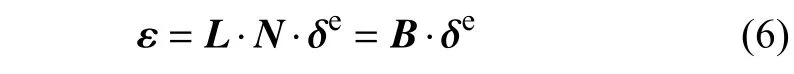
其中δe是由原子位移确定的节点的位移矢量，应变-位移矩阵B可以分割为

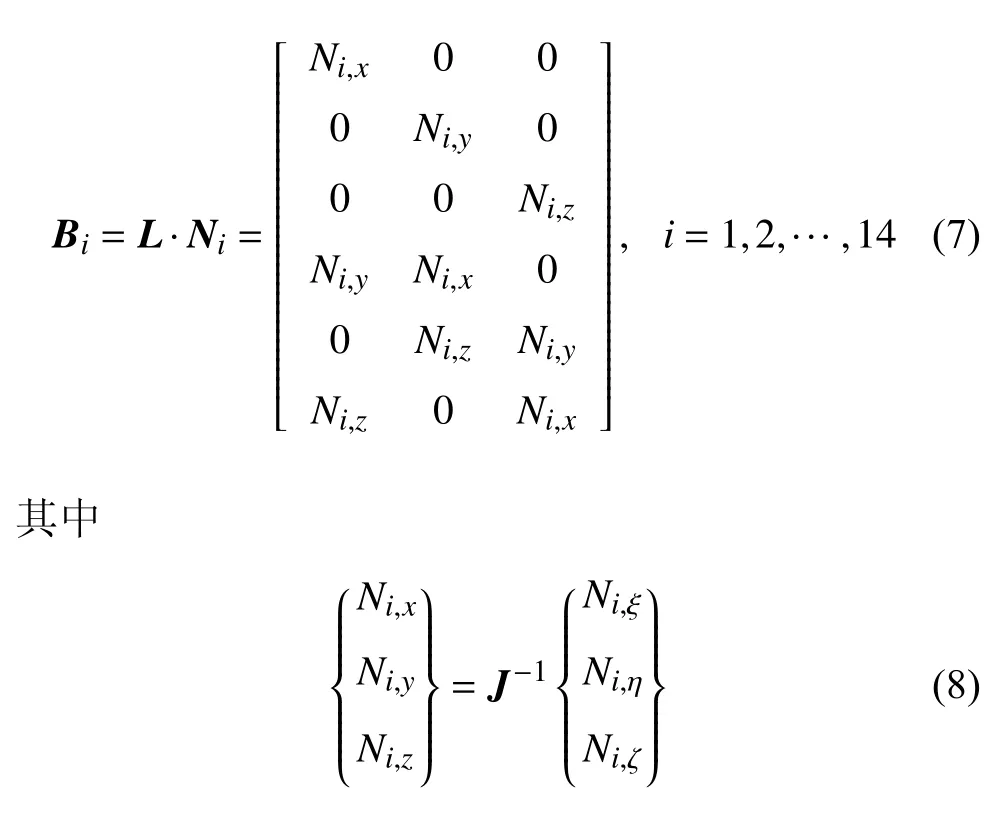
雅可比矩阵J描述了实际单元与等参元的坐标转换关系.

如果考虑材料为线性弹性情况，单元的应力场与应变能密度分别为

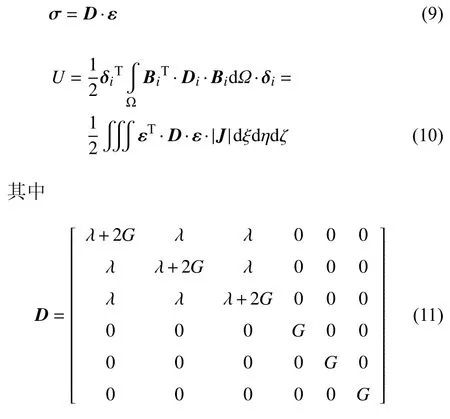
可应用式(4)、式(6)和式(9)通过节点位移插值直接计算单元内高斯点处的位移、应变和应力.若考虑3 × 3 × 3 的高斯积分点方案，则单元内有27 个高斯积分点(通常简称高斯点).

2 MD-FEA 方法的应用

下面通过两个典型物理问题的研究，通过比较本文MD-FEA 方法的结果与MD 模拟结果，以检验本文方法的有效性.

2.1 软硬两种金属(Al/Ni)等截面纳米杆串联结构的拉伸问题

研究的问题如图2 所示.

首先采用分子动力学软件LAMMPS[26]建立由Al 和Ni 构成的双材料纳米杆拉伸模型，原子间的相互作用采用EAM 势函数[26-27](见式(3)).整个系统由233 568 个原子(93 296 个Al 原子和140 272 个Ni 原子) 构成，模型在x方向上长为44 nm (Al 和Ni 段的长度各为22 nm)截面为边长8 nm 的正方形.模型的初始构型如图2 所示.Al 和Ni 晶体的[1 0 0]晶向与x轴平行，模型在x方向的两端设为刚体，y，z方向的4 个面为自由表面.整个系统在NVT 系综下保持温度为0.01 K.

图2 Al/Ni 双材料纳米杆拉伸分子动力学模型.界面及端部标注为黄色Fig.2 Molecular Dynamics model of the Al/Ni composite nano cylinder system.The interface layers and the boundaries are marked yellow

需要指出的是，许多研究[28-30]表明，实际情况下的Al/Ni 界面十分复杂，难以进行准确的原子模型建模.为了方便研究，Gurtin 与Murdoch[31]建立了简化的材料表/界面模型:假定材料的表/界面厚度为0 且具有一定的力学性质，并在连续介质力学框架下根据这个模型建立了材料的表/界面弹性理论.根据这个假设，同时也为了简化计算，在本模型中，Al 和Ni 在界面处各取一层原子层，并在x方向上进行固定，使得界面原子在运动中整体保持在同一平面内.界面处原子的相互作用采用L-J 势式(2)，以改变不同工况下的界面性能.另外，在纳米杆拉伸模型中，通常采用杆整体的应变变化作为外部载荷，由于计算规模的限制，应变率通常在106～ 108s-1之间.而在本模型中，为了保证界面在变形过程中保持平面，限制了界面原子在x方向的位移，Al 和NI 之间的变形无法通过界面进行有效地传递.因此，本模型采用力加载的方式，在模型x方向两端施加p=160.2 N/s 的外部载荷取代模型整体的应变加载，系统在整个加载过程中保持平衡.系统的时间步长设为0.001 ps.由图3 的应变-时间关系可知，Al，Ni 两相的应变率分别为4×107s-1和1.7×107s-1，并且在整个模拟过程中基本保持一致.

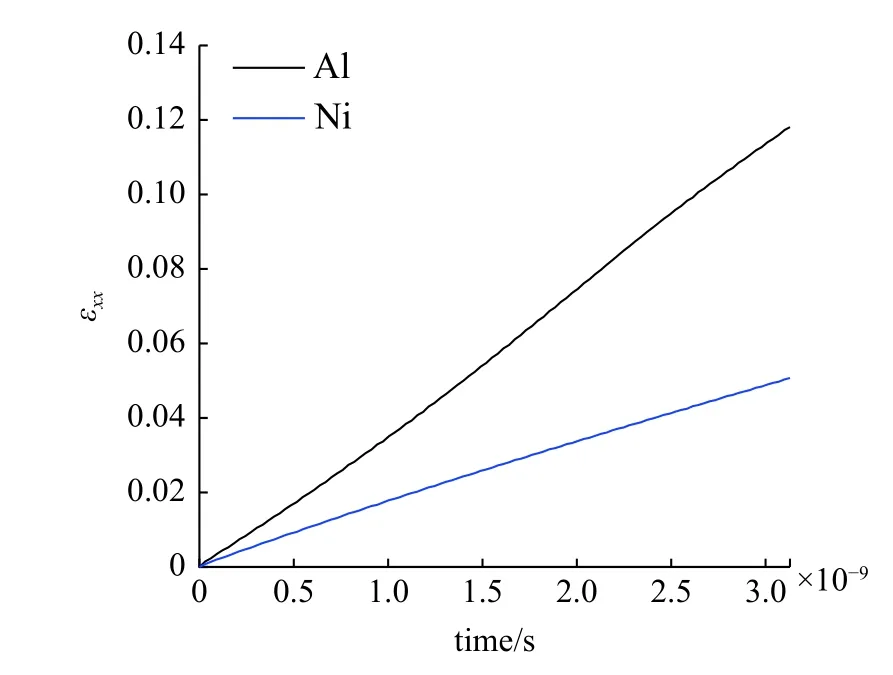
图3 拉伸载荷下Al 和Ni 的应变-时间曲线Fig.3 The strain-time relation of Al and Ni under uniform force loading

模型中Al 和Ni 的应力应变曲线如图4 所示.在达到极限应力σxx=7.56 GPa 之前，Al 和Ni 整体上都符合弹性变形.

达到极限应力后，Al 在界面附近发生破坏，如图5 所示.

图5 超过极限应力σxx=7.56 GPa 后Al-Ni 系统的变形Fig.5 Deformed Al-Ni system after the critical tensile stress σxx=7.56 GPa

根据模型的应力-应变关系，可知Al 和Ni 的杨氏模量分别为72.2 GPa 与134.6 GPa，这与其他研究[27，32]中，根据EAM 势的下的Al 和Ni 体积模量分别为79 GPa 和181 GPa，泊松比分别为0.35 与0.385计算所得的弹性模量分别为71 GPa 和125.3 GPa 相近.整个模型在弹性阶段的杨氏模量为92.1 GPa.

通过MD-FEA 方法计算模型每个单元高斯点处的拉伸应变εxx代表整个模型的连续应变场.在极限应力σxx=7.56 GPa 下，模型在z=4 nm 处的x-y截面的拉伸应变εxx如图6 所示，界面位置为x=0 nm，边界位置分别为x=-22 nm 和x=22 nm.材料Al内部的拉伸应变为0.12，材料Ni 内部拉伸应变为0.05，与图4 的结论一致，而在材料的界面和端部，由于边界条件的影响，拉伸应变与材料内部有所区别.

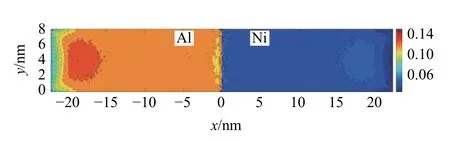
图6 拉伸载荷σxx=7.56 GPa 下，Al 和Ni 在中截面处的应变εxx，界面位置为x=0 nmFig.6 εxx at the middle section of Al and Ni under σxx=7.56 GPa.The interface at x=0 nm

图6 为材料在z=4 nm 处的中截面的拉伸应变εxx.在截面上，材料Al 和Ni 从模型底部(y=0 nm)到模型中部(y=4 nm)的应变分布如图7 所示.应变在刚体边界附近趋向于零，并朝着材料内部急剧增加，并经过少许的降低后，在材料Al 和Ni 的体内分别稳定在0.122 和0.053.在材料的界面附近，材料Al 处的应变随着与界面距离的减少整体上有少许的降低，而材料Ni 处的应变有少许增加，且与体内应变相比具有较大的分散性.界面附近应变的变化集中在距离界面4 nm 内的区域中.

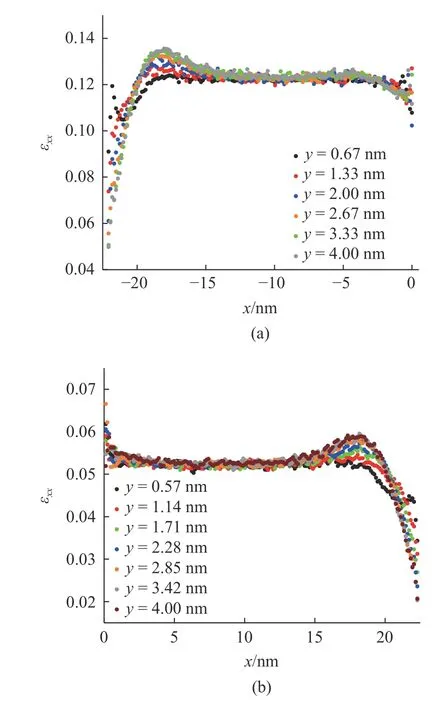
图7 材料中截面内不同位置的拉伸应变.(a) Al，(b) NiFig.7 Tensile strain in (a) Al and (b) Ni at the different location of the middle section

在相同的拉伸应力下，界面附近的拉伸应变εxx在材料Al 处的降低和材料Ni 处的升高主要是由于材料性能的不同引起的.根据EAM 势函数的结论与应力应变关系曲线，可知Al 和Ni 在[1 0 0]晶向上的杨氏模量分别为72.2 GPa 和134.6 GPa，泊松比分别为0.35 和0.385.因此，Al 和Ni 在y方向平行于界面的正应变分别为

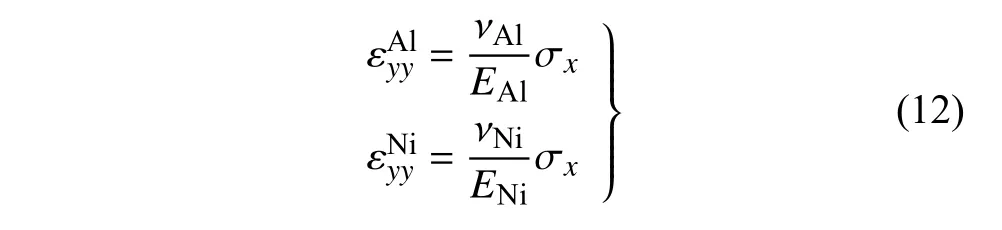
设Al 和Ni 在界面处平行于界面的正应变的差值为失配应变

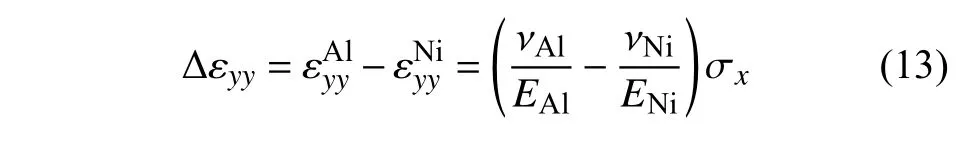
根据界面处的无滑移边界条件，需要在界面处引入额外的平行于界面的正应力，以保证在x=0 的界面处，满足

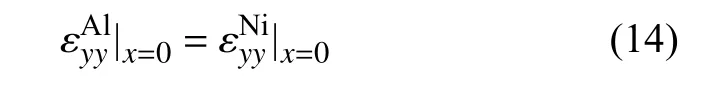
假设界面处完全是弹性变形，且界面两边材料中额外引入的应力使得界面整体保持平衡.因此

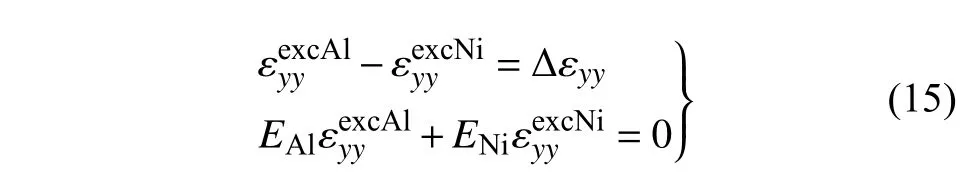
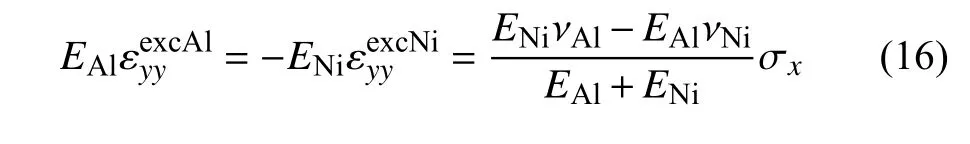
在z方向上同理.由此可得Al 和Ni 在x方向上的拉伸应变

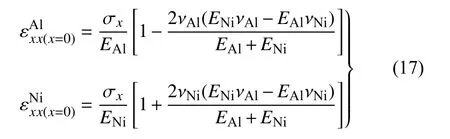
由式(18)计算可得，模型中Al 在x 方向上的拉伸应变在界面处减小6.5%，Ni 的拉伸应变在界面处增大7.2%，这与图7 的结论一致.

在分子动力学模拟中可以得到模型的原子应变.根据文献[16-17]的研究，原子的应变可以通过变形梯度计算得到

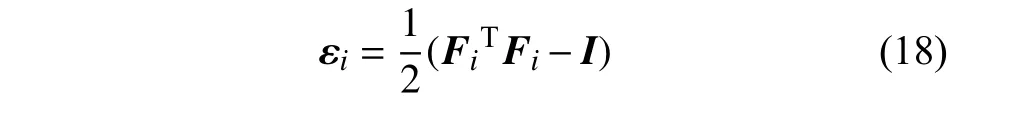
变形梯度Fi通过求下式的最小值得到

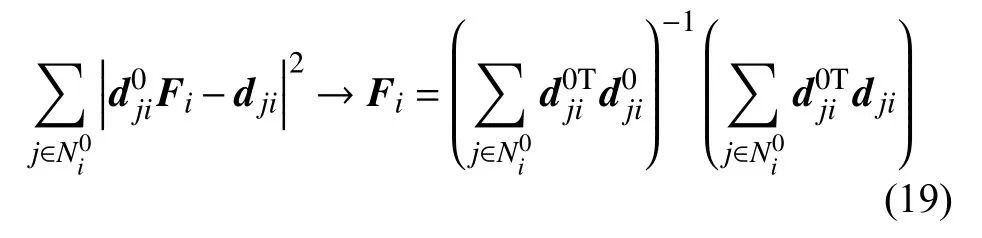
其中dji和分别为即时构型和初始构型下原子j到原子i的矢量.计算原子应变的截断半径设为0.7 nm，且不设置加权函数.拉伸载荷下，在模型的整体拉伸应变从0.02 到0.08 的变形过程中，通过两种方法计算得到的模型中心(y=z=4 nm)处沿x方向的拉伸应变εxx如图8 所示.使用MD-FEA 方法计算得到的材料内部的拉伸应变(MF)与通过变形梯度计算的原子应变(AS)在模型整体应变达到0.12之前基本相同.在之后的变形过程中，原子应变计算的拉伸应变大于使用MD-FEA 方法得到的拉伸应变.这主要是由于MD-FEA 计算了在弹性变形中常用的小应变张量，而原子应变基于变形梯度计算的是格林-拉格朗日应变张量.这两种应变在变形较小时的差异可忽略不计，但对于计算应变达到0.12 的材料Al，其结果有明显的差异.

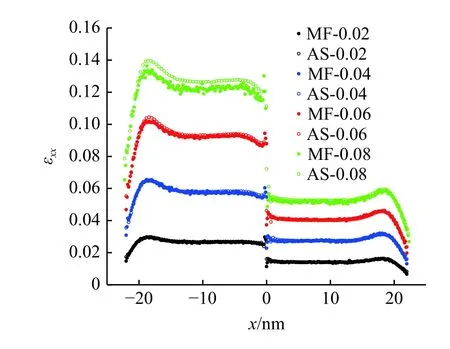
图8 模型整体应变0.02～0.08 的变形过程中MD-FEA 方法计算的应变与原子应变的对比Fig.8 Strain computed by MD-FEA method and deformation gradient with the system strain from 0.02 to 0.08

同时，本文计算了7.56 GPa 拉伸载荷下，模型中心在截断半径0.4～0.7 nm 下原子应变计算的拉伸应变值，如图9 所示.不同截断半径下，计算的原子拉伸应变在模型端部和体内基本保持一致，但在距离界面2 原子层内产生明显的差异.考虑到图7 所示的两种材料的拉伸应变在界面附近的横截面内有较大的分散性，可以认为这种复杂的应变分布是导致不同截断半径下计算得到的界面处的拉伸应变有较大差异的主要原因.

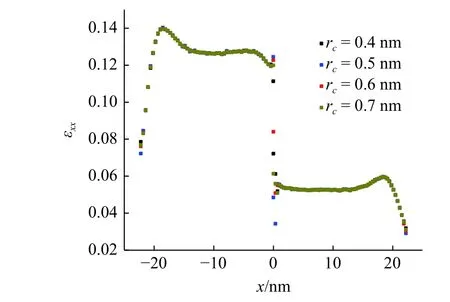
图9 不同截断半径下计算的原子应变Fig.9 Atom strain computed in different cutoff radius

在模型两端均匀的拉伸载荷下，材料Al 和Ni 在界面附近的拉伸应变在同一横截面内表现出一定的周期性变化，如图10 所示.除了由于应力集中出现在4 个角落的最大应变外，在材料Al 界面附近第2 层原子处，中心附近的拉伸应变大于四周边界附近的拉伸应变，边界附近的部分区域有着较大的拉伸应变，并在靠近材料内部时急剧减小.第2 层Ni 原子处，四角附近的拉伸应变大于材料中心区域，并且有规律地，在某些位置的拉伸应变明显减小.在两种材料界面附近的第4 层原子处，大致能观察到与各自第2 层原子处相反的应变分布，且应变在横截面内的变化幅度明显减小.这表明界面附近的拉伸应变场在平行与垂直界面方向上都有波动，且随着与界面距离的增加，波动幅度逐渐降低.在距离界面第6 层原子处，应变波动基本消失，除边界附近应变与内部稍有变化外，材料内部的应变与远离界面的应变基本相同.

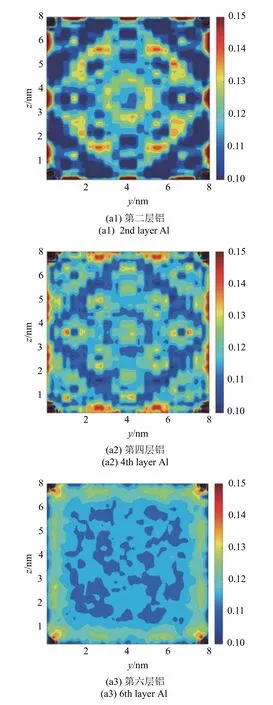
图10 (a) Al 和(b) Ni 在距界面第2，4，6 层截面原子处的拉伸应变Fig.10 Tensile strain of the 2nd，4th and 6th layers of the cross section near the interface for (a) Al and (b) Ni

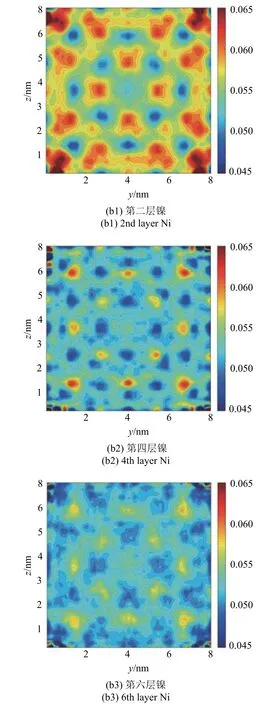
图10 (a) Al 和(b) Ni 在距界面第2，4，6 层截面原子处的拉伸应变(续)Fig.10 Tensile strain of the 2nd，4th and 6th layers of the cross section near the interface，for (a) Al and for (b) Ni (continued)

界面原子在弛豫过程中发生重构时，在对其应力应变的研究中也观察到了类似的波动现象[33].但是，本文选择了弛豫后的构型为参考构形，消除了弛豫过程中残余应变的影响，这表明界面处的应变波动也会由外部施加的拉伸载荷引起.材料Al 在横截面上有20 × 20 个晶格，材料Ni 有23 × 23 个晶格.界面处的晶格失配与应变波动的周期相吻合.因此可以认为界面的原子失配不仅仅引起界面处的残余应变，同时也改变了界面处的材料性能，使得界面截面的不同位置在相同的拉伸载荷下产生不同的拉伸应变.

拉伸应变在界面附近处的剧烈变化是原子应变在不同的截断半径下得到的结果产生巨大差异的主要原因之一.图11 展示了Al 在距界面第2 层原子处的原子应变在不同截断半径下的分布，作为与MD-FEA 方法得到的结果(图10(a1))的对比.截断半径rc设置在0.35～0.38 nm 之间.结果显示截断半径rc=0.36 nm 和rc=0.37 nm 下的原子应变分布与MD-FEA 方法的结果有相似之处，而rc=0.35 nm和rc=0.38 nm 的结果却截然不同.同时，相比于MD-FEA 方法，原子应变的分布规律显得较为粗略，忽略了许多细节.对于FCC 晶体，每个晶体单元拥有4 个原子，因此每个单元根据原子位移得到4 个原子应变值，而MD-FEA 方法准确计算了每个单元在27 个高斯点处的应变，因此能够提供更多的应变细节，得到的应变场也更加精确.

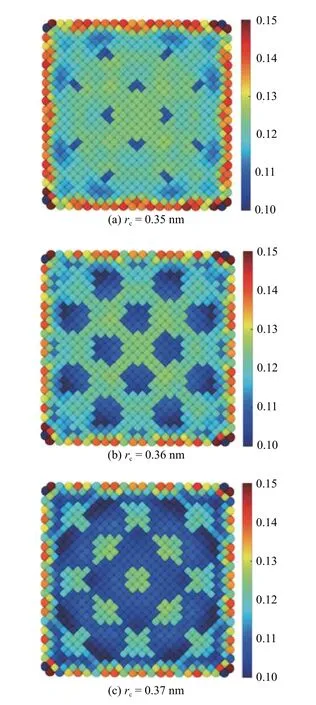
图11 截断半径为0.35～0.38 nm 时，距界面第2 层Al 原子截面处的拉伸应变分布Fig.11 Atom strain at 2th layer in phase Al with the cutoff radius rc from 0.35 to 0.38

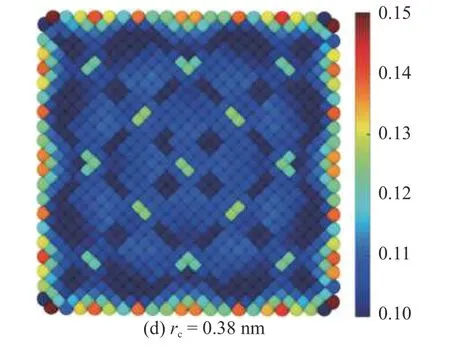
图11 截断半径为0.35～0.38 nm 时，距界面第2 层Al 原子截面处的拉伸应变分布(续)Fig.11 Atom strain at 2th layer in phase Al with the cutoff radius rc from 0.35 to 0.38 (continued)

当计算一种材料的原子应变时，截断半径内可能同时包含其他材料的原子，这也会明显影响计算的结果.如图12 所示，当计算界面附近Al 原子的应变时，截断半径内参与计算的不仅有附近的Al 原子，同时也包含了部分Ni 原子.随着截断半径的增大，使得界面附近的Al 原子计算结果误差也随之增大.在相同的拉伸载荷下，材料Al 的应变明显大于Ni 的应变，这使得界面附近Al 原子的应变随着截断半径的增大而减小，Ni 的原子应变随截断半径的增大而增大.

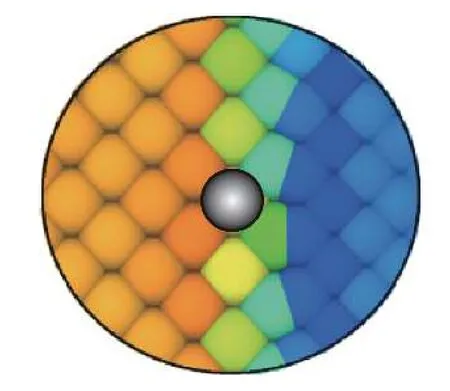
图12 rc=0.8 nm 下，界面原子附近参与原子应变计算的Al 原子(黄色和橙色)和Ni 原子(绿色和蓝色)数量示意图Fig.12 A schematic diagram of the number of atom Al (yellow and orange) and Ni (blue and green) that participated in the calculation of the atom strain of the selected atom near the interface with rc=0.8 nm

以距界面第2，4，6 层原子层截面处中线上(z=4 nm)的拉伸应变为例，在7.56 GPa 的拉伸载荷下，由MD-FEA 方法计算的结果与不同截断半径下原子应变的结果如图13 所示.

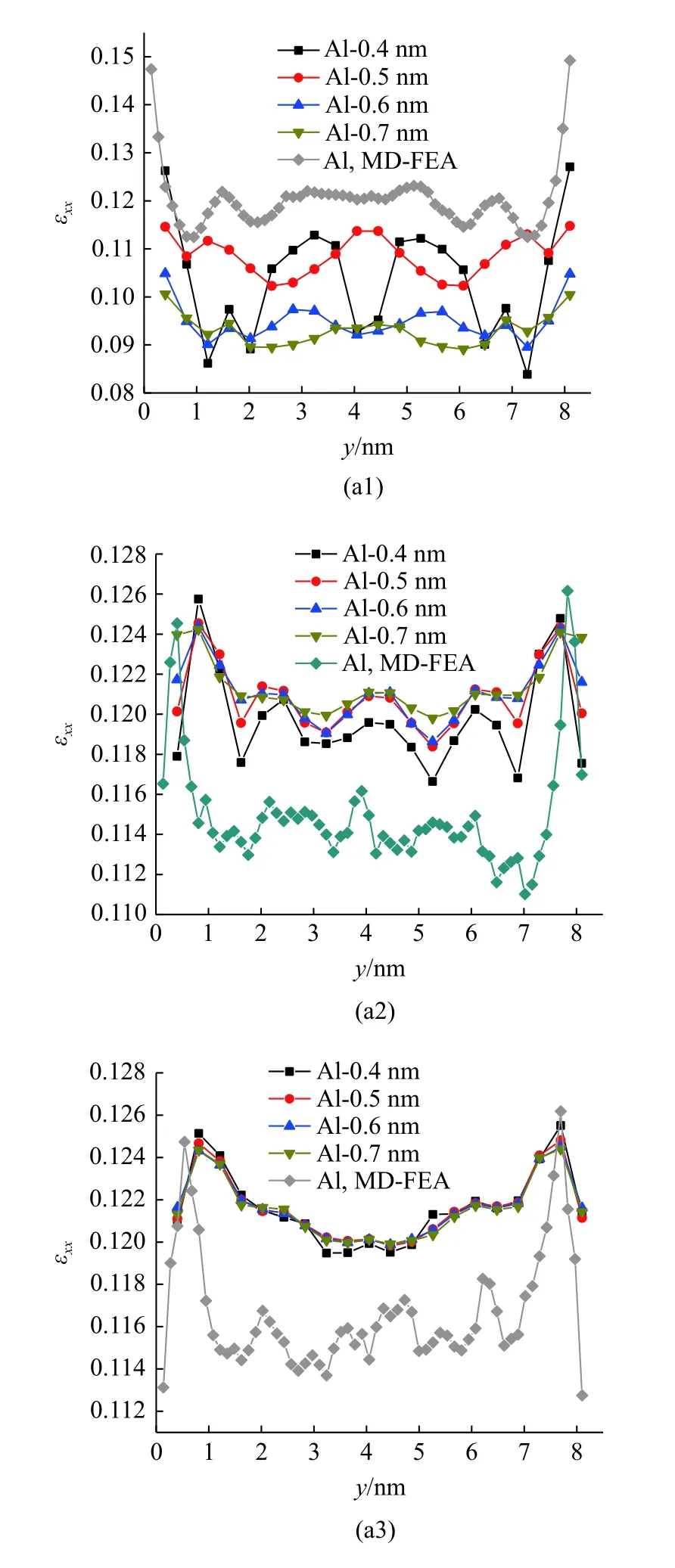
图13 不同截断半径下，距离界面第2，4，6 层原子层截面中线上的(a1)-(a3) Al 原子和(b1)-(b3) Ni 原子的原子应变分布以及同一位置下MD-FEA 方法计算的应变Fig.13 MD-FEA strain and atom strain of the 2nd，4th and 6th layers of (a1)-(a3) Al and (b1)-(b3) Ni in the middle line of interface section computed by different cutoff radius

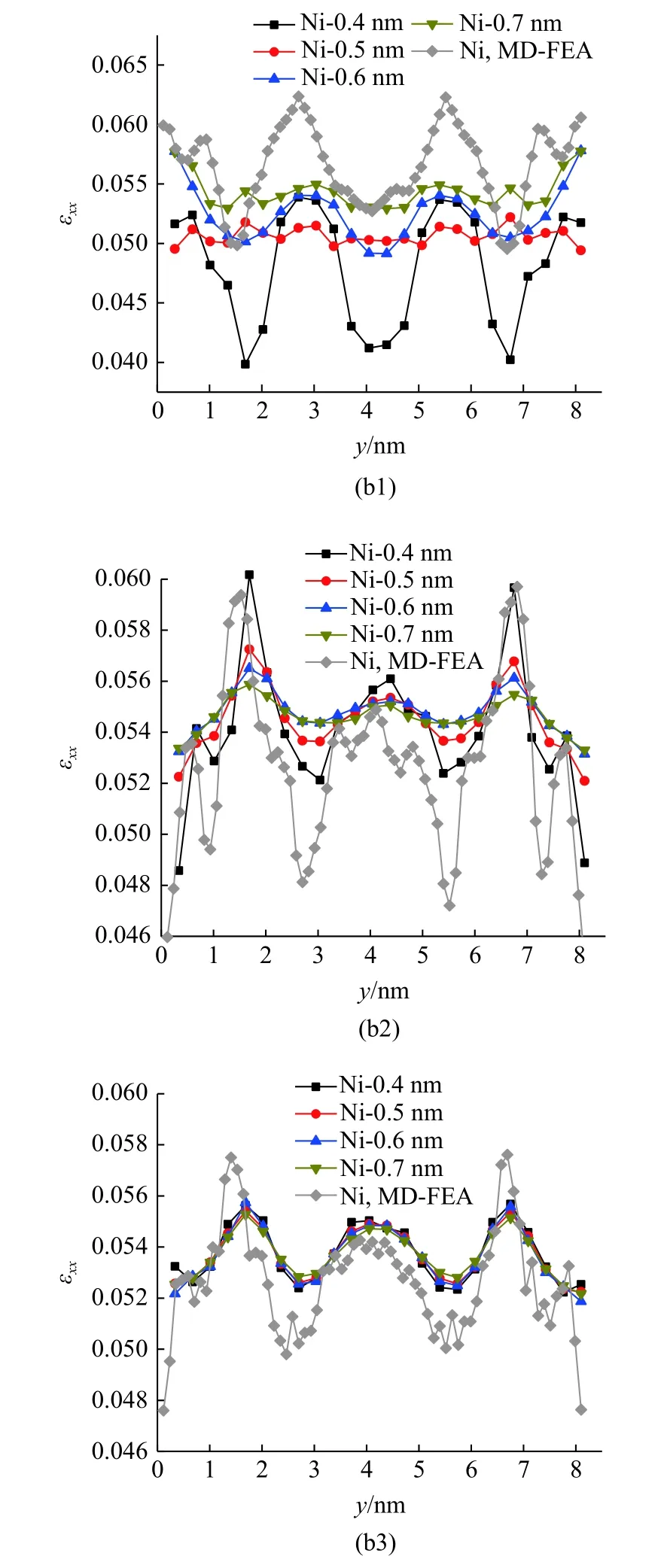
图13 不同截断半径下，距离界面第2，4，6 层原子层截面中线上的(a1)-(a3) Al 原子和(b1)-(b3) Ni 原子的原子应变分布以及同一位置下MD-FEA 方法计算的应变(续)Fig.13 MD-FEA strain and atom strain of the 2nd，4th and 6th layers of (a1)-(a3) Al and (b1)-(b3) Ni in the middle line of interface section computed by different cutoff radius (continued)

在截断半径为0.4 nm 时，距离界面第2 层原子层的截面内计算的Al 和Ni 原子应变表现出明显的波动，并且随着截断半径的增大，这种波动幅度明显减小.同时，随着截断半径的增大，Al 的平均原子应变呈现逐渐减小的趋势，而Ni 的平均原子应变逐渐增大.在此截面上，通过MD-FEA 方法计算的应变大于原子应变的计算值，且在截面中线上，应变的变化趋势也与某一特定截断半径下的原子应变类似(rc=0.6 nm 的Al 与rc=0.4 nm 的Ni).而在距离界面第4 层原子层处，不同截断半径下计算的原子应变较为一致，随着截断半径的增大，Al 和Ni 原子的原子应变计算值均稍有增大，在距离界面第6 层原子层处，不同截断半径下计算的原子应变基本相同.在第4 层与第6 层原子层处，原子应变的计算值均大于MD-FEA 方法的计算值，而这两种方法计算的应变沿着截面中线的变化趋势较为一致，且原子应变的变化幅度明显小于MD-FEA 方法计算的应变.随着与界面距离的增加，不同方法计算的Al 原子的应变稍有增大，Ni 原子的应变稍有减小，这与图7 和图8的结论相吻合.

在MD-FEA 方法中，应变是以参考构型中的一个单元为基本单元计算的，这种方法消除了人为选取的截断半径的影响.单元的体积由材料的晶格常数确定，每个单元的节点(原子)数量相同，且单元的体积足够小，从而能得局部的精确结果.在MDFEA 方法中，每个单元都只包含了同一种原子，界面附近的Al 原子只能通过相互作用改变界面另一边Ni 原子的构型来间接反应对Ni 原子的影响，而不能Al 原子构型的变化直接参与Ni 原子处应变的计算，反之亦然.用这种方法计算界面附近的应变场更加合理.

图14 展示了模型在1.26 GPa 的拉伸载荷下中截面的应力分布.位力应力由下式计算得到

其中mi，vi分别为原子i的质量与速度，rij，fij分别为原子i与原子j之间的距离与作用势，V为原子体积.

根据图14(a)和图14(b)可知，MD-FEA 方法计算的应力明显大于原子的位力应力.在加载的拉伸应力为1.26 GPa 时，MD-FEA 方法计算的Al 和Ni 在模型体内的应力为1.32 GPa 见图14(a)，而位力应力计算的应力值明显较小，且在两种材料中并不一致见图14(b).这主要是由于在MD-FEA 方法中，选择弛豫后的构型为参考构形，而在参考构形中计算的位力应力有一定残余的压应力存在见图14(c).

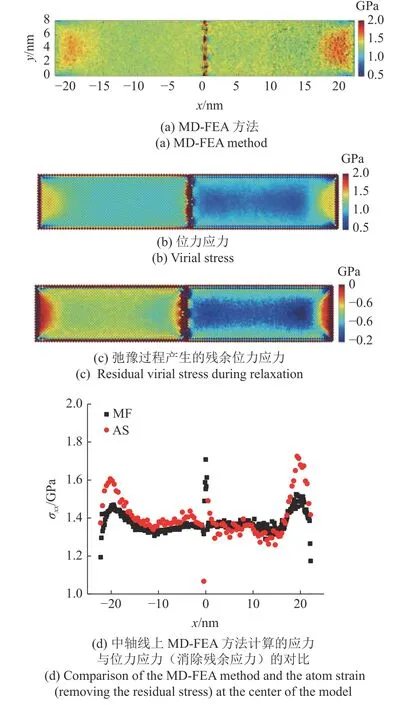
图14 拉伸应力为1.26 GPa 时，不同方法计算的模型中截面应力分布Fig.14 Distribution of the stress on the cross section computed by different methods under the applied tensile stress 1.26 GPa

图14(d)展示了MD-FEA 方法与消除了残余应力的位力应力在模型轴心处的对比，可见两种方法计算的结果较为一致.在使用MD-FEA 方法计算应力时，假设模型的杨氏模量和泊松比在变形过程中保持不变，而通过模型的应力-应变关系可知，材料的杨氏模量在变形较大时有轻微的变化.因此，鉴于选取的材料参数为小变形下的参数，可以认为用MD-FEA 方法计算的应力在模型的变形较小时较为精确.同时，MD-FEA 方法计算的应力在模型的表面与内部较为一致，而位力应力的结果显示了由于邻近的原子构型的差异，在同一拉伸载荷下，模型表面原子和内部原子计算的应力有显著的差异.因此，MD-FEA 方法更能准确地计算模型的应力分布.

2.2 金刚石压头/Al 基体的纳米压痕实验分析

使用分子动力学软件LAMMPS 建立纳米压痕模型，基体长和宽分别为40 个晶格，高为15 个晶格的Al，压头为由半径为10 nm 的金刚石球形压头.初始构形中压头尖端与基体表面距离为1.156 nm，并在每时间步中对压头施加0.05 晶格的位移(约0.02 nm) 后，对整个模型弛豫.模型中的Al 基体采用EAM 势[27]，金刚石压头采用tersoff 势[34]，Al 和金刚石之间的相互作用使用L-J 势描述，其中，结合能ε=31.5×10-3eV，平衡距离为2.976 Å，截断半径为10 Å[35].基体的底部与四周为固定边界，整个系统采用NVE 系综.温度设定为0.01 K.模型的初始构型见图15(a).图15(b)展示了载荷与压入深度D之间的关系.

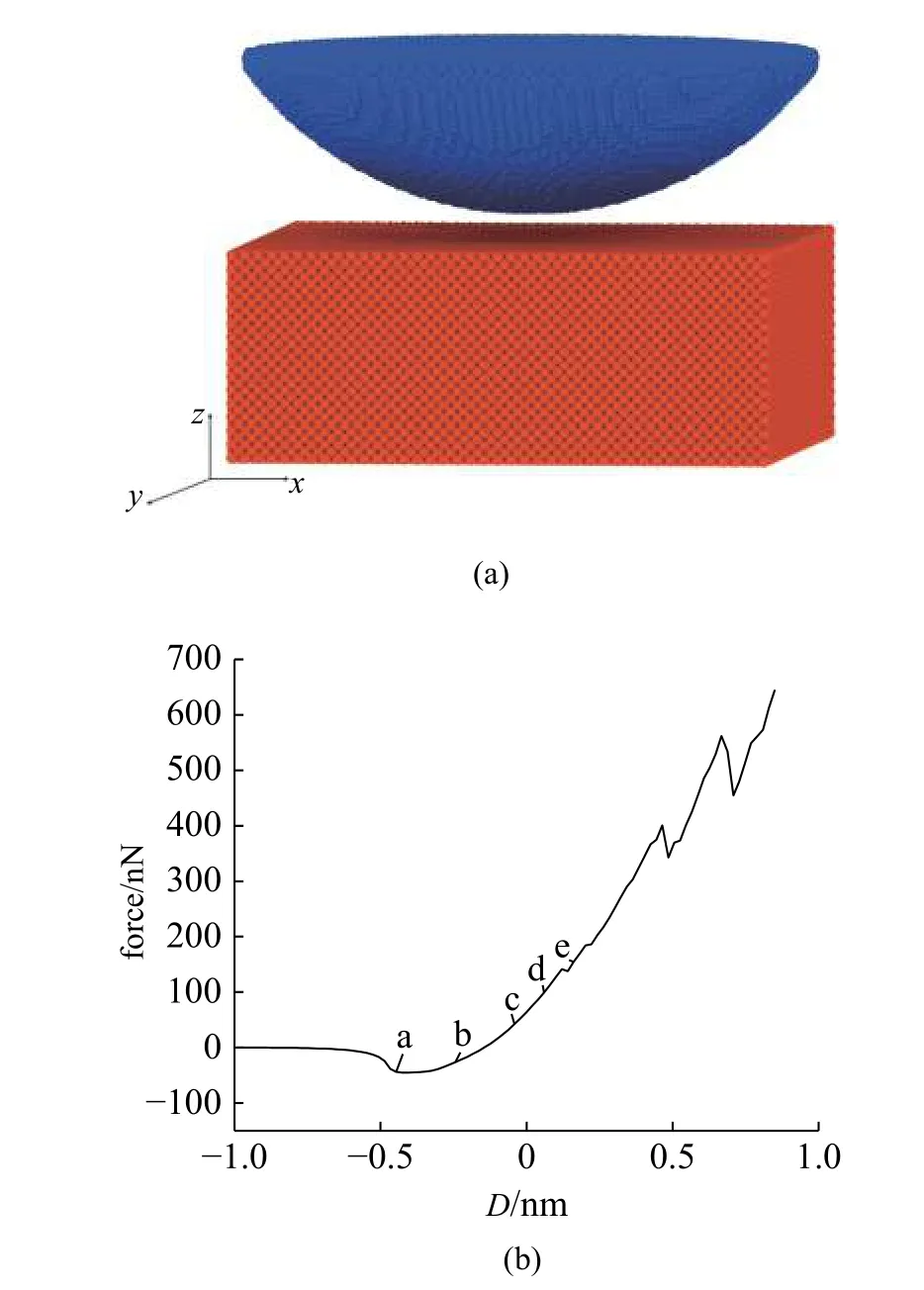
图15 (a)纳米压痕的分子动力学模型和(b)载荷-压入深度曲线Fig.15 (a) Molecular dynamics model of the indentation and (b) the force-depth relation during the simulation

从D=-0.55 nm 开始，基体和压头之间表现出相互吸引，压头受到基体向下的拉力，并在D=-0.4 nm 时达到最大值.直到D=-0.1 nm 时，拉力转变为压力，且在D=0.15 nm 之前不断增大，在D=0.15 nm时压力出现第一次波动，基体开始出现位错，此时压力为150 nN.

基体的应变分量εxx和γxz在临界压入深度下的分布如图16 所示.在这两种计算方法中，εxx的影响区域较为接近，而MD-FEA 方法计算的反对称的剪应变γxz的大小和影响范围都明显大于原子应变的结果.

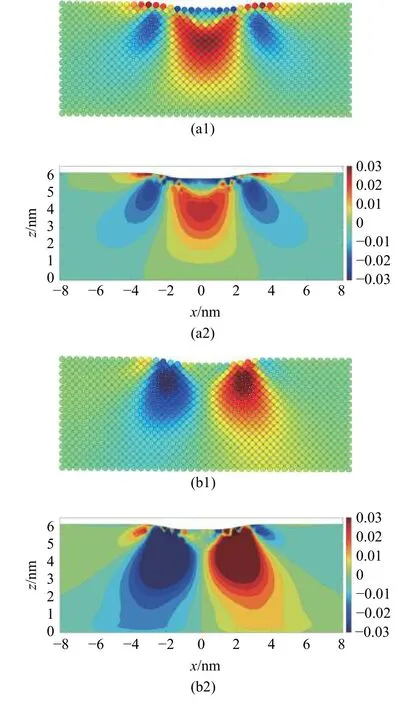
图16 MD-FEA 方法计算的应变分量(a1)-(a2) εxx 与(b1)-(b2) γxz 和对应原子应变的对比Fig.16 Comparison of (a1)-(a2) εxx and (b1)-(b2) γxz computed by the atom strain and MD-FEA method

图17 展示了用MD-FEA 方法计算的基体中截面在压痕过程中，位错出现前的各个阶段(图15(a)-图15(e))的应变场，并与原子应变进行了对比.计算原子应变的截断半径取为rc=0.45 nm.

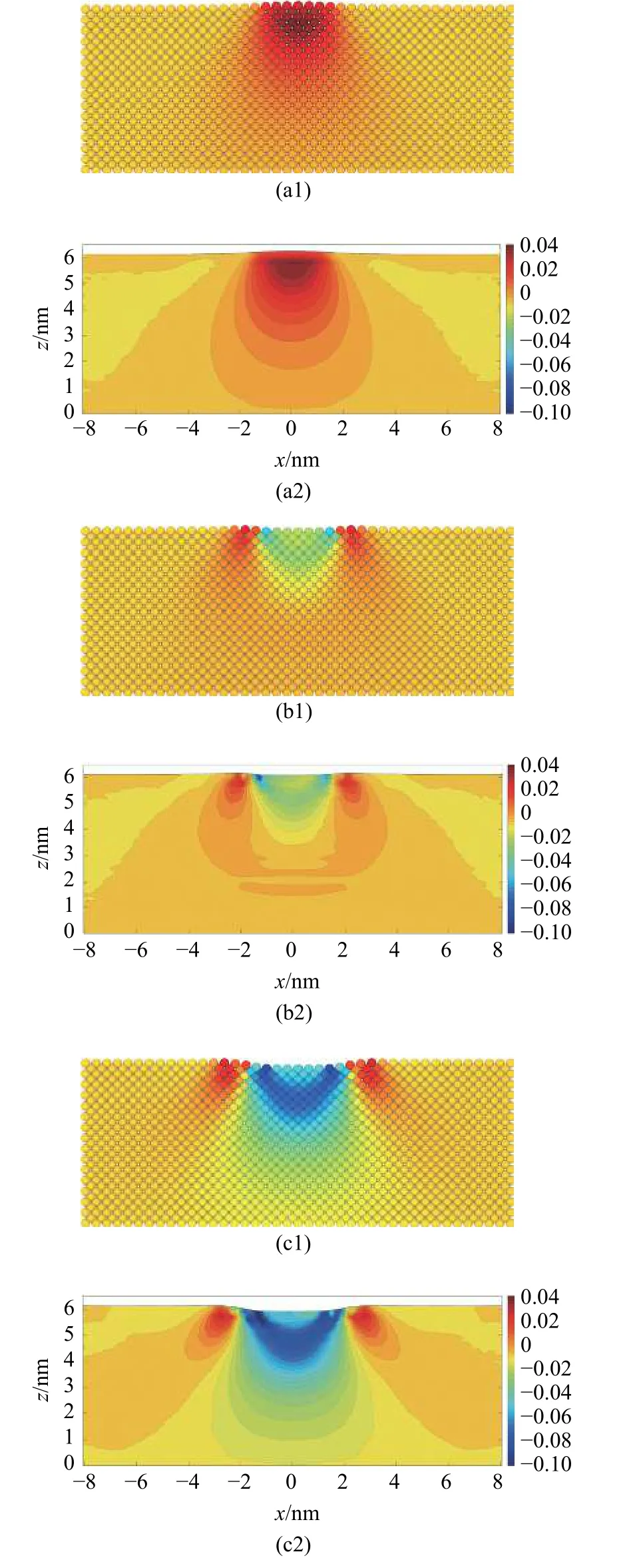
图17 压痕过程中(a1)-(e1)原子应变与(a2)-(e2) MD-FEA 应变分量εzz 的对比Fig.17 (a1)-(e1) Atom strain and (a2)-(e2) the strain field computed by MD-FEA method of εzz during the indentation

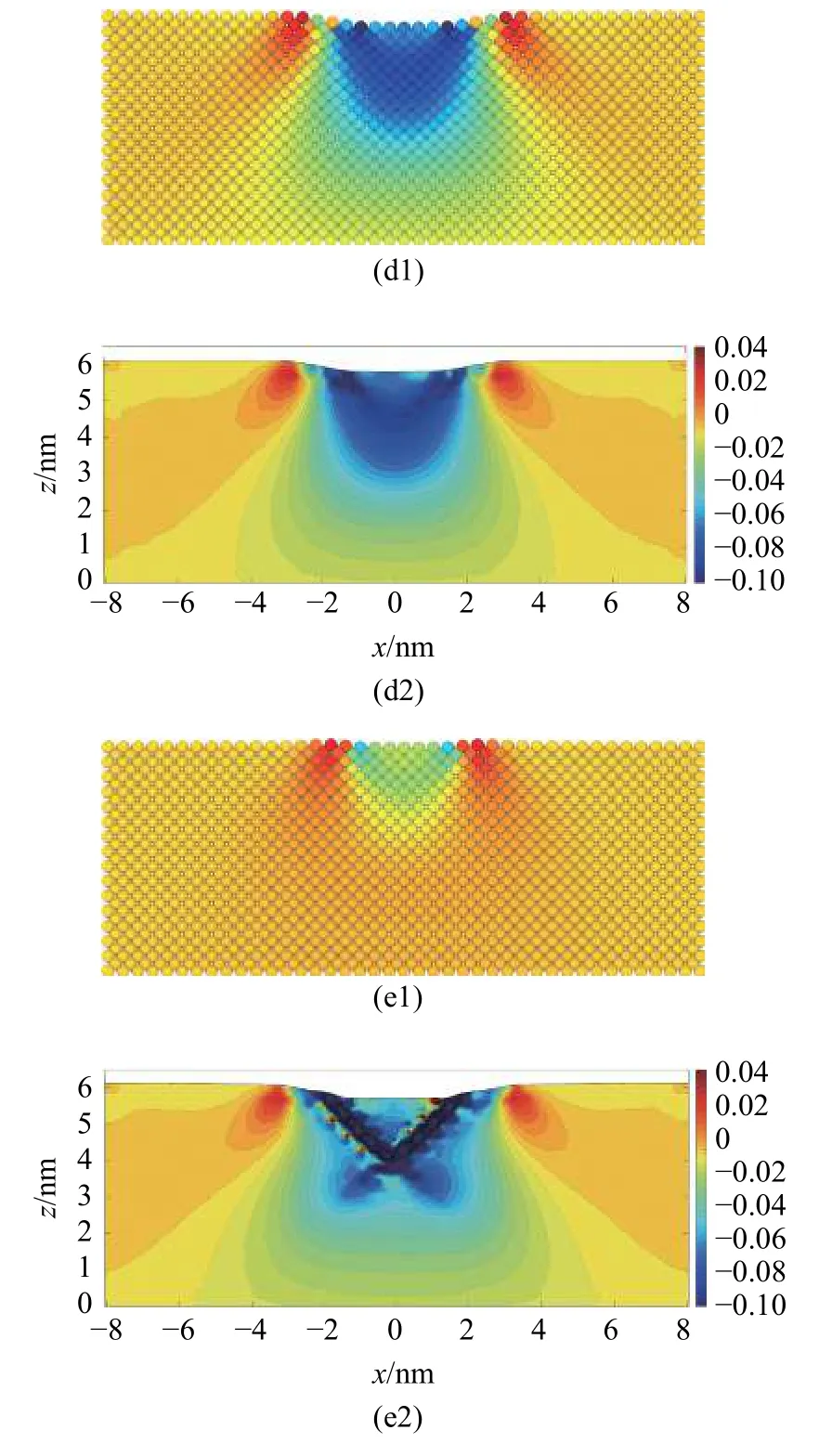
图17 压痕过程中(a1)-(e1)原子应变与(a2)-(e2) MD-FEA 应变分量εzz 的对比(续)Fig.17 (a1)-(e1) Atom strain and (a2)-(e2) the strain field computed by MD-FEA method of εzz during the indentation (continued)

由MD-FEA 方法计算得到的基体内部的应变场εzz和原子应变的结果基本相同.基体的应变主要集中在压头下方，并随着压入深度的增加不断扩大.压坑周围出现一圈拉伸应变区域，并随着压入深度的增加不断往外扩张，这与其他研究的结论类似[36].在压入深度为0.1 nm 位错出现之前，压缩应变主要分布在压痕表面下方约3.5 nm 的区域内，压缩应变的最大值并不在压痕与基体的接触表面，而是出现在压痕表面下方约1 nm 的区域中.在出现位错时，位错位置计算得到的应变值显著增大，因此能明确判别出位错产生的位置.

由两种方法计算得到的基体中心的应变分量εzz和εxx的在压痕过程中的对比如图18 所示.在应变较小时，MD-FEA 方法计算得到应变值和原子应变完全一致，在应变较大时，MD-FEA 方法计算的压应变εzz较原子应变稍大.应变分量εzz和εxx的最大值都出现在压头下方的基体内部而不是压痕表面，且这两者出现的位置并不一致.εzz的最大值出现在压痕表面约1 nm 的位置，而εxx的最大值出现在压痕表面约1.5 nm

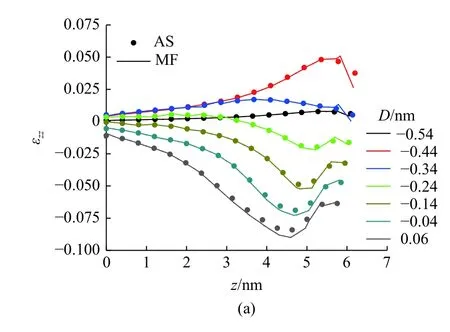
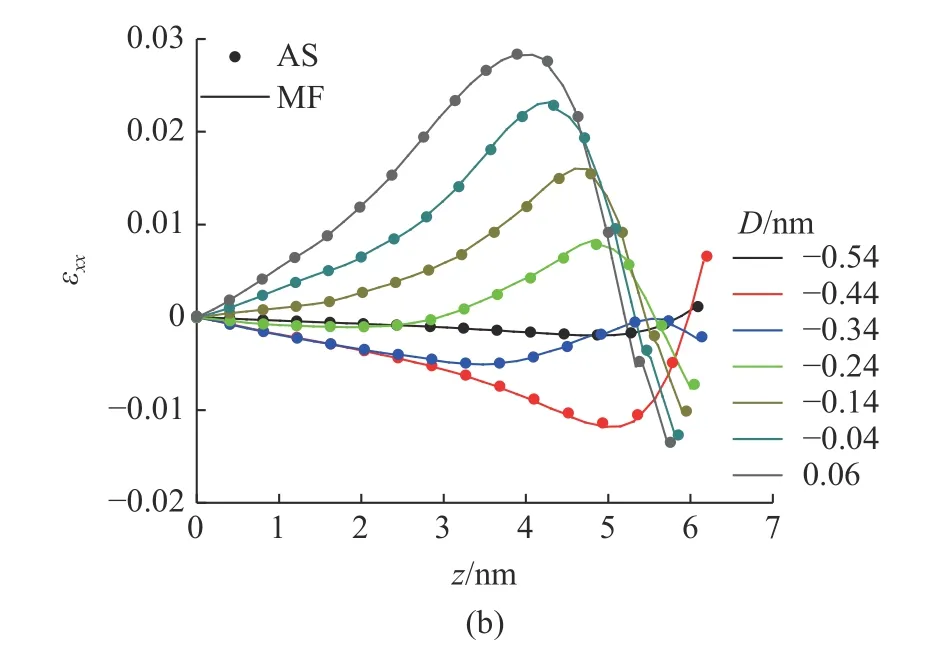
图18 由MD-FEA 应变和原子应变在基体中心处的应变分量εzz 和εxx 的对比Fig.18 Comparison of εzz and εxx at the center of the substrate between MD-FEA method (MF) and atom strain (AS) during the indentation

截断半径在计算压痕过程中基体原子应变的影响较小.在截断半径rc=0.4 nm 和rc=0.8 nm 下计算的基体中截面的应变分布如图19 所示，应变分量εzz和εxx在不同截断半径下的结果在基体内部基本一致，仅在压痕表面的原子处有所差异.rc=0.8 nm 下计算的应变分量εzz在压痕表面的值较rc=0.4 nm 时稍大，而分量εxx在压痕表面的值则较rc=0.4 nm 时稍小.这种差异在分析压痕过程中基体的整体变形时可忽略不计，但在关注压痕表面的变化时必须加以考虑.

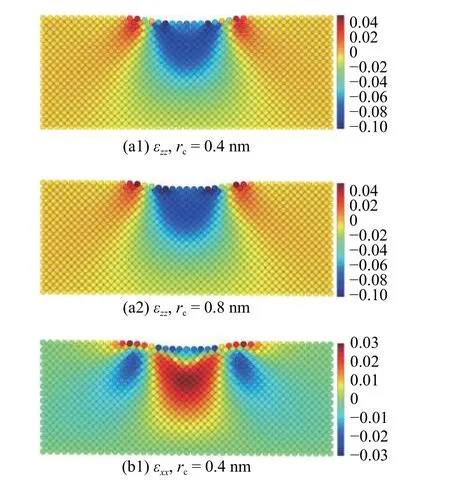
图19 截断半径rc=0.4 nm 和rc=0.8 nm 下中截面上的原子应变分量(a1)-(a2) εzz 与(b1)-(b2) εxx 分布图Fig.19 Atom strain of (a1)-(a2) εzz and (b1)-(b2) εxx with the cutoff radius rc=0.4 nm and rc=0.8 nm

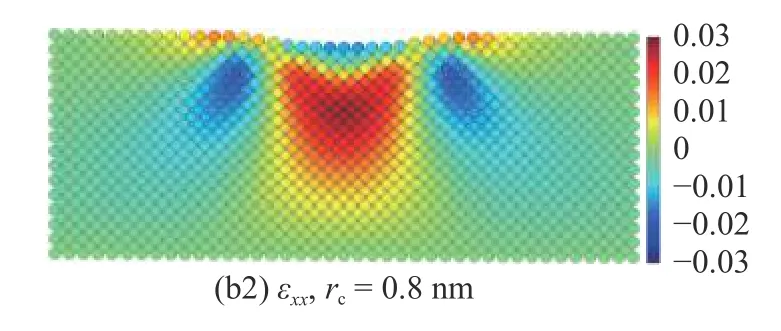
图19 截断半径rc=0.4 nm 和rc=0.8 nm 下中截面上的原子应变分量(a1)-(a2) εzz 与(b1)-(b2) εxx 分布图(续)Fig.19 Atom strain of (a1)-(a2) εzz and (b1)-(b2) εxx with the cutoff radius rc=0.4 nm and rc=0.8 nm (continued)

图20 展示了由两种方法计算的基体中心不同深度的应力分量σzz和σxx在压痕各阶段的对比.在位力应力的计算中，基体的杨氏模量设为72.2 GPa，泊松比为0.35.σzz在基体不同深度均有体现，σxx则主要影响了距离压痕表面2 nm 以内的区域.除了基体表面位力应力计算不准确的部分，两种方法计算的基体内部的应力在变形较小时基本一致，在变形接近产生位错的临界状态时，计算的位力应力值略大于MD-FEA 方法计算的结果.

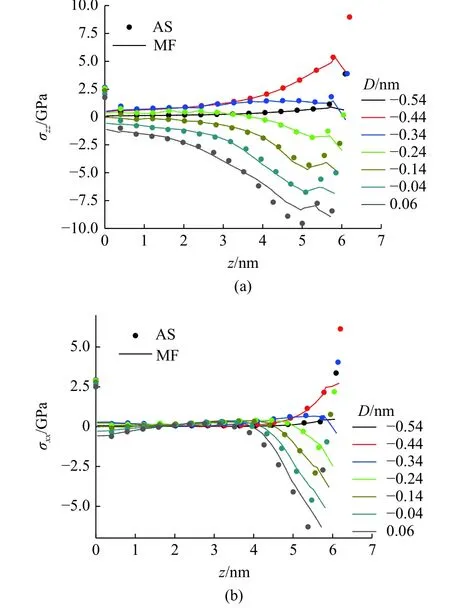
图20 压痕过程中由MD-FEA 方法(MF)计算的应力分量与位力应力(AS)分量σzz 和σxx 的对比Fig.20 Comparison of σzz and σxx between MD-FEA method (MF) and atom virial stress (AS) during indentation

图21 展示了由MD-FEA 方法计算的图15(b)中从a～e 状态下的正应力σzz在中截面处的分布，并与对应位置处原子的位力应力进行了对比.由于原子构型的差异，基体表/界面处原子的位力应力结果与体内原子有明显差异，因此明显影响了压痕表面的应力结果.忽略起始阶段由于压头与基体相互吸引产生的拉应力，基体最大压应力出现在压痕表面下方，且比同一状态下最大压应变εzz出现的位置更接近压痕表面.在产生位错的临界状态下，压应力σzz的最大值达到10 GPa.

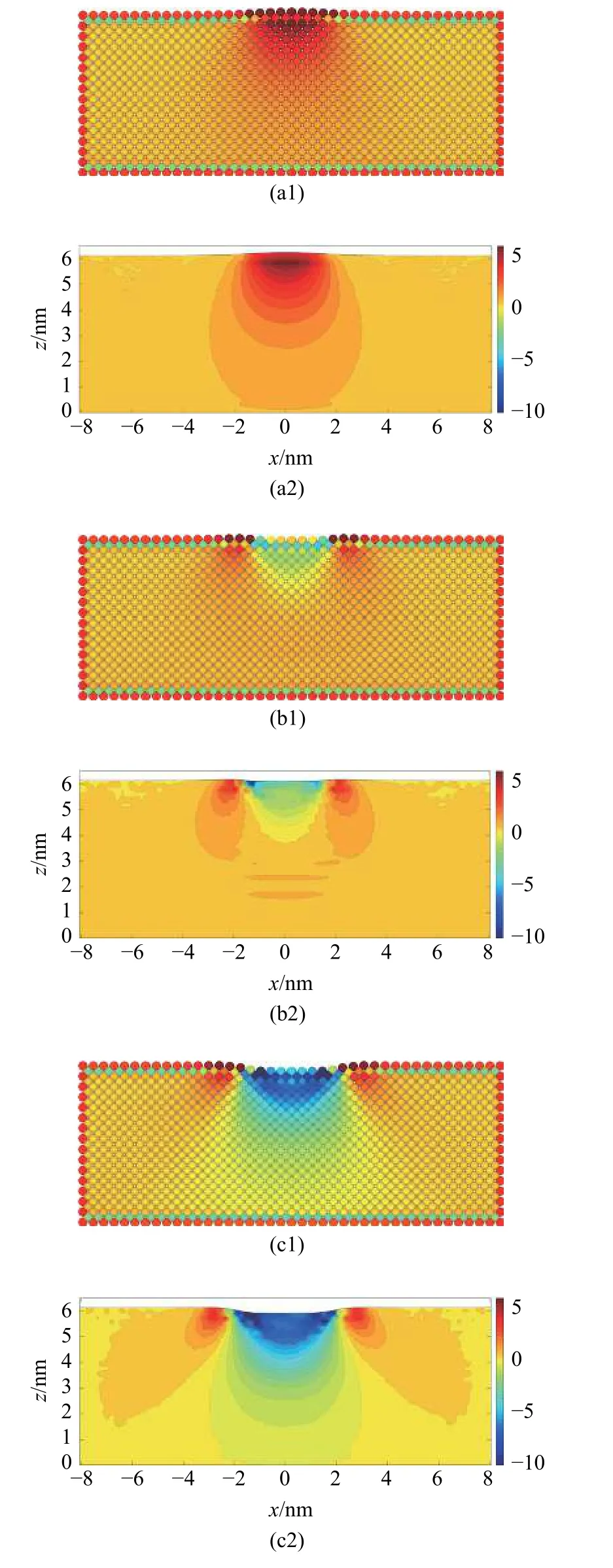
图21 压痕过程中基体截面处(a1)-(e1)原子位力应力与(a2)-(e2) MD-FEA 应力场的对比Fig.21 (a1)-(e1) Virial stress and (a2)-(e2) the stress field computed by MD-FEA method on the middle section of the substrate during indentation

图21 压痕过程中基体截面处(a1)-(e1)原子位力应力与(a2)-(e2) MD-FEA 应力场的对比(续)Fig.21 (a1)-(e1) Virial stress and (a2)-(e2) the stress field computed by MD-FEA method on the middle section of the substrate during indentation (continued)

3 结论及讨论

本文提出了一种通过结合分子动力学(MD)和有限元分析(FEA)来计算原子模型中的应力和应变的新方法(MD-FEA).这种方法通过离散的原子坐标和位移数据，计算连续介质力学框架下的计算连续的应力和应变场.本文通过建立Al/Ni 双材料纳米杆拉伸模型和金刚石压头/铝基体的纳米压痕模型，将MD-FEA 方法计算得到的应力/应变场和在传统的原子模型中广泛使用的位力应力，以及通过离散的变形梯度计算得到的原子应变进行对比.结果显示，在模型体内，MD-FEA 方法计算的应变分量和原子应变相一致，但在原子位移急剧变化的模型表/界面上有明显的差异.这主要是由于原子应变在计算过程中平均了邻近原子的应变，且包含了截断半径内不同类型，材料参数有差异的原子.除了模型表/界面处由于原子构型的差异，位力应力计算不准确外，MD-FEA 方法计算的应力与位力应力在模型体内变形较小时完全一致.由于MD-FEA 方法通过杨氏模量和泊松比将原子模型中的应力和应变相联系，在大变形下，由于材料参数可能发生变化，计算的应力不精确.因此通过这种方法计算应力时应限定在小变形下.

结果显示:在应变较为均匀的区域，MD-FEA 方法计算的应变场与基于MD 变形梯度计算的原子应变相一致，而在界面附近应变变化剧烈的区域，MDFEA 方法能够提供精确的应变场，而原子应变只能得到较大范围内的平均值.用MD-FEA 方法计算的应力场与位力应力在模型体内相一致，但在模型界面与表面区域，由于邻近原子的构型发生变化，位力应力的计算有很大的误差，而MD-FEA 方法仍能得到准确的应力场.MD-FEA 方法避免了用应变梯度算法计算原子应变时截断半径的选取，以及计算位力应力时原子体积的确定，也不需要引入加权函数，消除了人为因素对应力应变结果的影响.同时，MDFEA 方法得到的是原子模型中连续的应力应变场，将离散的原子模型和传统连续介质力学理论框架之间建立了联系.

需要指出的是:按本文提出的计算模型，原子的位置完全是按照MD 计算给出的，所以本文方法与MD 计算结果对于原子的位移来说完全相同，而应变和应力则不同;本文将一个晶格处理为一个有限元单元，事实上这里的有限单元可以扩大至一个单元代表多个晶格的情况，只要初始划分的单元的节点能够与原子的初始位置对应即可，但此时由两种模型给出的应力和应变结果的差异将会更大一些，这个将在后续研究中作进一步研究和讨论.