双柱墩倒T 型钢盖梁结构设计及计算探析

■毛文浩

（福建省交设工程试验检测有限公司，福州 350007）

在城市高架桥梁设计中，在满足桥下净空要求前提下，降低桥梁设计标高能有效降低设计和施工难度，节约投资。 倒T 型盖梁以其能有效利用上部梁高范围内的结构高度的优势，在城市桥梁设计中被广泛采用。 目前，倒T 型盖梁以混凝土盖梁为主，但其设计较复杂、施工难度大，现浇施工周期长，对下部交通影响大。 钢盖梁结构较轻，能够在工厂分段预制，现场拼接后整体吊装施工，尤其是在跨越地面道路时，能有效缩短封闭交通的时间，减缓施工给交通带来的压力，因此，钢结构盖梁具有一定的优势。

钢盖梁作为一种新型的盖梁形式，目前对其研究较少，但其构造复杂，与混凝土盖梁有较大差异，因此，有必要对其进行分析研究。 以某市政桥梁双柱墩倒T 型钢盖梁为研究对象，采用有限元分析软件Midas 对其进行总体计算， 以及软件Ansys 对小箱梁和组合梁支座位置局部加劲、钢混结合段位置局部构造进行了分析，为类似钢盖梁的设计提供了借鉴。

1 钢盖梁设计概况

某城市高架桥梁一处钢盖梁，对应桥面宽度为33.0 m， 其下地面辅道宽为15.5 m。 小里程侧接30 m 预应力砼小箱梁， 大里程侧接50 m 钢混简支组合小箱梁。

桥墩采用混凝土双柱墩， 立柱中心距19.5 m，盖梁悬臂长度约5.5 m。 立柱尺寸为1.6 m×2.2 m（横桥向×顺桥向）。钢盖梁截面采用倒T 形，中心高3.6 m，宽3.64 m。 倒T 高1.9 m，宽1.5 m，双向2%横坡。立柱上部2.6 m 为钢混结合段。支座位置根据上部结构进行布置。 钢盖梁构造见图1。

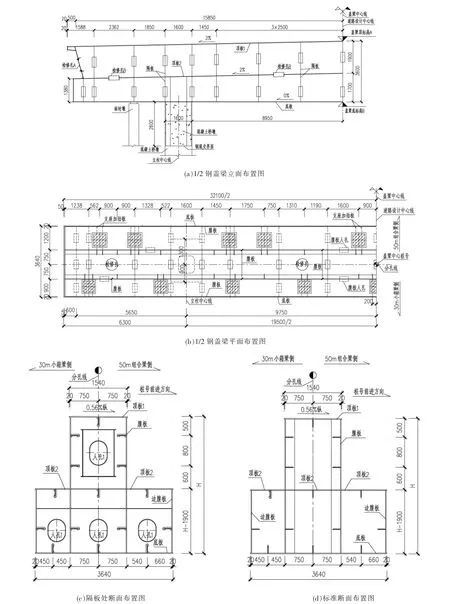
图1 钢盖梁构造

盖梁采用Q345qD 钢材， 立柱采用C50 混凝土。 各板件厚度根据受力需要，在不同位置分别为：顶板厚度为16、25 mm，中间顶板厚度为12 mm，中腹板厚度为16、22 mm，边腹板厚度为16 mm，底板厚度为12、16、22 mm。受压加劲板采用刚性加劲肋。

钢盖梁主要施工步骤如下：（1）立柱施工，并设置临时墩；（2）钢盖梁在工厂预制后，现场整体吊装，由临时墩支撑；（3）钢盖梁与混凝土立柱连接处施工，连接处施工完成后拆除临时支墩；（4）施工二期恒载，施工上部结构。

2 钢盖梁总体计算

钢盖梁总体计算采用有限元分析软件Midas按平面梁单元，建立有限元模型进行计算。 其计算方法与上部结构计算方法类似，但在活载的处理上略有不同。

2.1 设计荷载

钢盖梁所承受的恒载包括：盖梁自重、上部梁体恒载、桥面铺装、防撞栏杆、声屏障、中央分隔带荷载。 汽车荷载为城-A 级，以上部结构单车道荷载纵向布载在盖梁产生的支反力为集中力，在盖梁上按八车道横向加载， 并考虑多车道横向折减系数。整体升降温参照 《公路桥涵设计通用规范》(JTG D60-2015)[1]第4.3.12 条取用。 梯度温度按照英国桥梁规范（BS5400）计算。 沉降按5 mm 考虑。 荷载组合按 《公路桥涵设计通用规范》(JTG D60-2015）进行组合验算。

2.2 计算模型

在Midas 中， 将整个盖梁结构划分为50 个单元，53 个节点。 盖梁单元与桥墩单元刚接， 墩底固结。 截面上、下翼缘考虑局部稳定和剪力滞影响下的有效分布宽度。 钢盖梁计算模型图见图2。

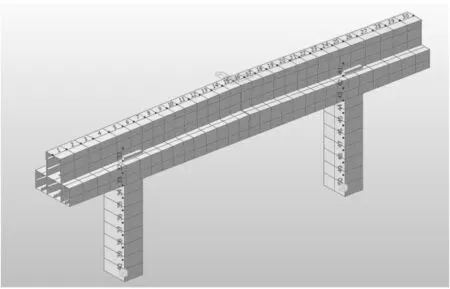
图2 钢盖梁计算模型图

2.3 应力计算结果

根据计算结果，将各施工阶段顶、底板正应力结果列于表1。

表1 各施工阶段板件最大正应力(单位：MPa)

对于剪应力计算， 假设剪力全部由中腹板承担，得基本组合下剪力最大处剪应力和腹板变厚处剪应力分别为89.4、86.4 MPa。 根据以上结果，计算基本组合下顶、底板组合应力（表2），可见钢盖梁强度满足规范要求。

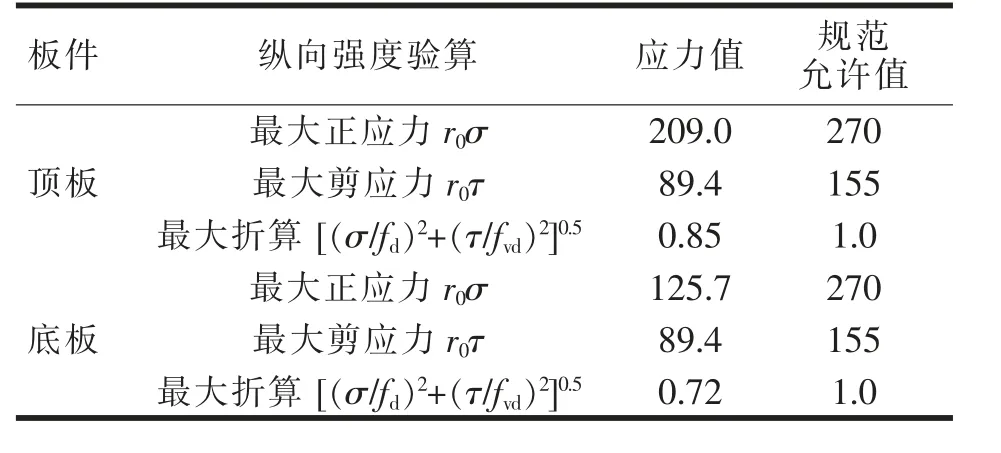
表2 钢盖梁各板件应力单位:MPa

2.4 稳定验算

2.4.1 整体稳定

倒T 盖梁在使用阶段侧向受上部结构和铺装约束，不存在整体稳定问题。 施工阶段受压翼缘自由长度L1与宽度B1之比为8.95/1.54=5.81＜13，满足《公路钢结构桥梁设计规范》（JTG D64-2015）[2]第5.3.2 条规定，不存在整体稳定问题。

2.4.2 板件局部稳定

针对顶板、底板、腹板局部稳定验算参照《公路钢结构桥梁设计规范》（JTG D64-2015）第5.1.5 条、5.1.6 条和5.3.3 条进行验算，结果均满足要求。

2.5 疲劳验算

根据 《公路钢结构桥梁设计规范》（JTG D64-2015）[2]第5.5.2 条规定，取疲劳模型I 进行疲劳计算。

盖梁小里程侧接30 m 预应力砼简支小箱梁，大里程侧接50 m 钢混组合简支小箱梁， 可偏保守取0.7Pk=0.7×360=252 kN，0.3qk=0.3×10.5=3.15 kN/m，可得单车道在盖梁处的作用活载值为：3.15×30/2+3.15×50/2+252=382.9 kN。 车辆荷载以集中力形式在盖梁按车道进行横向布置，可得疲劳效应值。 疲劳抗力根据疲劳细节由规范附录C 查的。疲劳验算根据规范第5.5.4 条计算（表3），可见盖梁顶、底板疲劳验算满足要求。

表3 钢盖梁疲劳验算结果

2.6 总体计算结果分析

根据以上计算结果，可得到以下结论：（1）钢盖梁强度、稳定性和疲劳性能满足规范要求。 （2）现有板厚条件下，恒载作用下顶、底板上下缘应力水平接近，说明已充分利用钢材拉压特性，板厚设置合理。 （3）与混凝土盖梁相比，钢盖梁安装完成即达到预期承载力，不存在预应力钢束分批张拉问题。 然而，总体计算只能根据规范要求对主要板件（顶板、底板、腹板）的局部稳定进行验算，对支座处及钢混结合段还需做深入分析。

3 支座位置局部构件测算分析

上述采用平面梁单元模型进行的总体计算仅能针对盖梁整体进行强度和稳定性分析，而对于局部构件的验算，需采用更加精细的有限元模型做进一步计算。

盖梁作为承上启下的重要构件，主要承受由支座传递的上部结构荷载。 因此，支座部位的可靠性尤为关键。 为较好地模拟支座位置附近相关板件的受力情况及局部稳定， 使用有限元分析软件Ansys建立支座位置局部板壳+实体模型。

3.1 有限元模型

3.1.1 计算长度

在选取计算节段时，应选取刚度较大的隔板截面作为局部模型边界条件的支承截面，以免支承截面畸变导致分析结果错误。 盖梁最大隔板间距为2.5 m， 故分别选取了L=2.5 m 及L=7.5m 两个节段进行了建模分析，结果表明两者分析结果一致。 因此，有限元模型计算长度可取2.5 m。

3.1.2 计算模型

模型采用三维实体+板壳有限元方法计算，其中钢构件用板壳单元（Shell63）模拟，支座垫板用实体单元（Solid95）模拟。 有限元模型共计约3.4 万个单元，3.4 万个节点。

3.1.3 荷载与边界条件

上部结构自重及二期荷载由每个支座平均分担。 防撞栏杆、声屏障、中央分隔带及车辆荷载应由相应梁片支座承担。 荷载以面荷载形式作用在支座垫板上。 有限元模型采用简支边界条件，在腹板底部约束。 有限元计算模型见图3。 图中X 方向为纵桥向，Y 方向为竖向，Z 方向为横桥向（下同）。

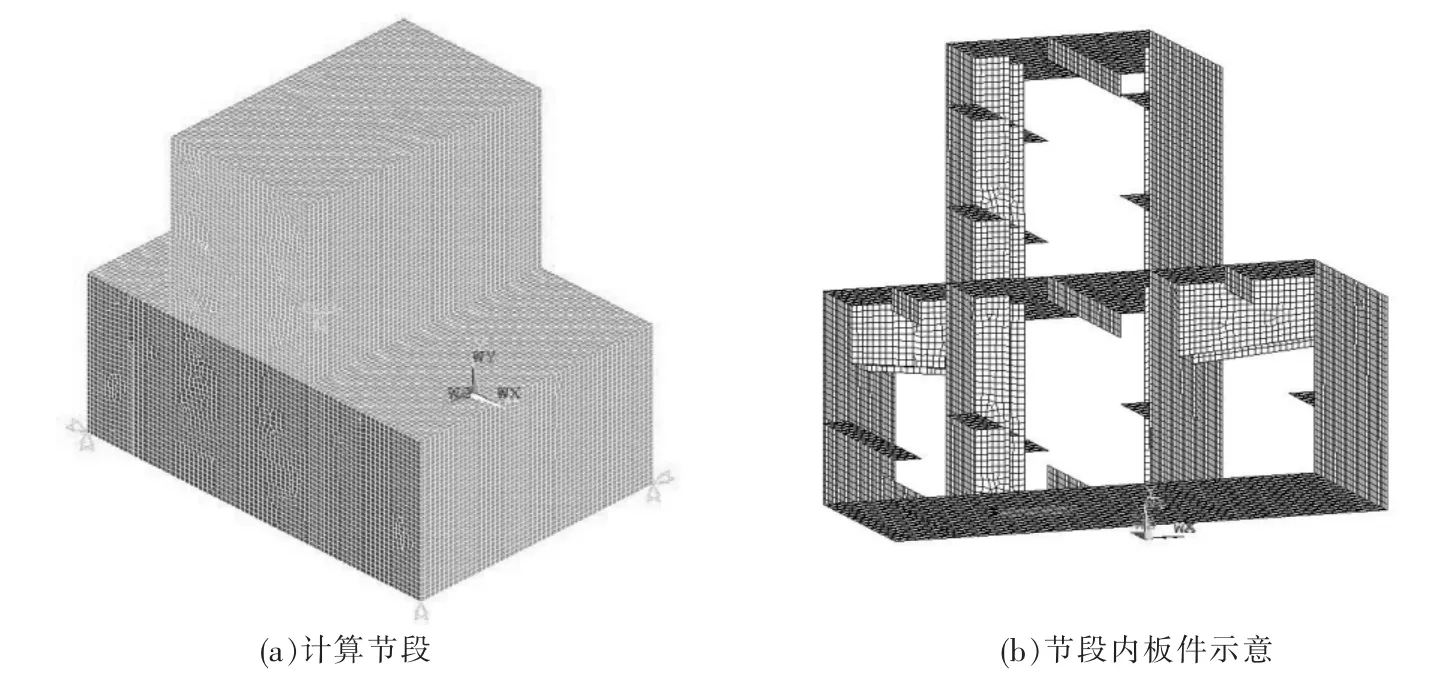
图3 支座位置局部分析计算模型

3.2 局部构造拟定

根据盖梁构造，可以初步判定支座所承受的荷载应通过最近路径传递，即荷载传力路径应是由支座垫板通过顶板2 及顶板加劲肋传递给两侧腹板。因此，拟定支座位置局部加劲构造见图4，包括2 块厚度为16 mm 的支座加劲板、2 块厚度为24 mm 的腹板横向加劲（考虑腹板局部稳定要求）以及1 块厚度为16 mm 的顶板2 加劲。

对于支座加劲板的布置， 除考虑受力需求外，还应考虑钢结构制造和焊接空间要求，以及满足后期检修时人员的通过性需要。 因此，本研究分别比较了不同支座加劲板间距B（图4a），以及不同顶板加劲尺寸h1和h2（图4b）对结构受力的影响，为设计提供参考。

图4 支座位置局部加劲构造

3.3 支座加劲板尺寸对局部受力的影响

本研究针对支座加劲板加劲间距B=300 mm时，不同h1和h2情况下的局部受力情况进行分析。分析工况包括： 工况1：h1=300 mm，h2=400 mm；工况2：h1=350 mm，h2=450 mm； 工况3：h1=400 mm，h2=500 mm；工况4：h1=450 mm，h2=550 mm；工况5：h1=500 mm，h2=600 mm； 工况6：h1=550 mm，h2=650 mm；工况7：h1=600 mm，h2=700 mm；工况8：h1=650 mm，h2=750 mm；工况9：h1=700 mm，h2=800 mm。

根据计算结果，各工况应力图相似，且组合梁侧应力较大。 因此， 仅给出工况1 组合梁侧各板件Mises 应力图（图5），由此可进行初步的定性分析。由应力图可见，支反力的传力路径与3.3 节所述一致，即支座加劲板为主要受力构件，其次是顶板2和腹板，腹板横向加劲及顶板2 加劲受力较小。 因此，本研究仅对顶板2、腹板及支座加劲板应力进行进一步分析。

图5 工况1 板件的Mises 应力图

3.3.1 支座加劲板应力分析

对于支座加劲板， 各工况Mises 应力图基本相似， 本研究给出工况2 和工况3 支座加劲板的Mises 应力图，分别见图6、7。

根据应力图可见，支座加劲板受力较大位置共4 处，详见图6。 其中，①②点为加劲板与支座垫板交接处应力集中点，③点为与腹板交接处应力集中点，④点为最大受力点。

由图6 和图7 可以看出，（1）荷载主要由支座垫石边缘开始，由顶板2 和支座加劲板向两侧腹板传递；（2）腹板受力变形引起加劲板底部受拉，即点④为加劲板受力最大处；（3）点③存在较大应力集中现象；（4）工况三中应力最大点由工况二的点④变化为点③，即加劲板尺寸的增大能把荷载更多地传递给腹板，减小加劲板受力，同时，也能减小应力集中的数值。

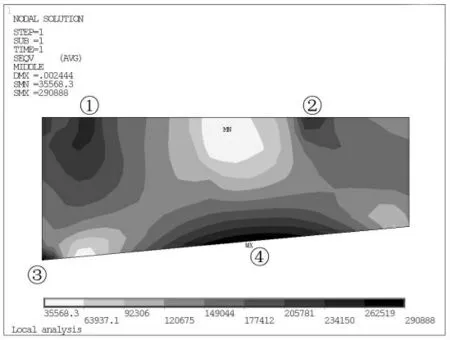
图6 工况2 支座加劲板Mises 应力图

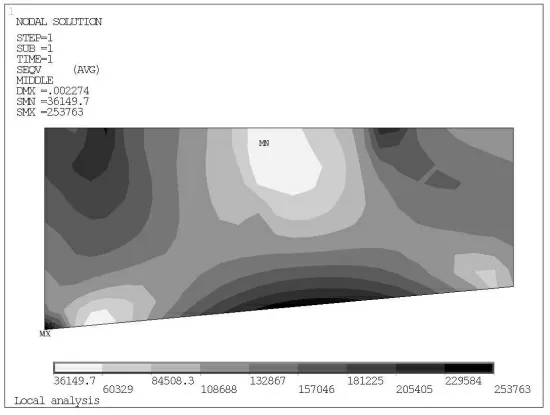
图7 工况3 支座加劲板Mises 应力图

图8 给出各工况下点④位置的Mises 应力值。可见，板件尺寸的增大在一定范围内对应力的影响最大（图中工况1～工况4），随着板件尺寸增大，对应力的影响效应减小。 根据应力计算结果，板件尺寸可取工况4 尺寸设计，即h1=450 mm、h2=550 mm。

图8 各工况点④Mises 应力曲线及稳定系数

3.3.2 稳定计算结果对比

稳定系数表示屈曲荷载系数，屈曲荷载等于该系数乘以所施加的荷载值。 各工况下的稳定系数见图8。 可见，对于支座位置局部模型，最小稳定系数为6，即当实际荷载达到设计荷载6 倍时，才会发生失稳现象。 因此，支座部位结构局部稳定性较好。

3.3.3 顶板2 及腹板Mises 应力

根据以上分析， 工况4 顶板2 及腹板Mises 应力图分别见图9 和图10。各工况下板件最大应力变化曲线见图11。

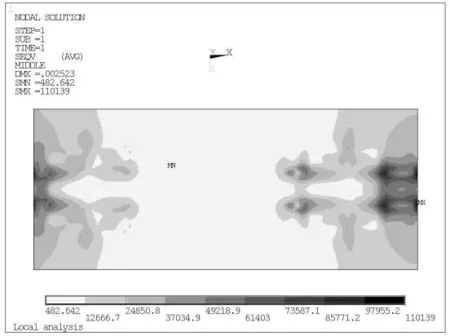
图9 工况4 顶板2 Mises 应力图

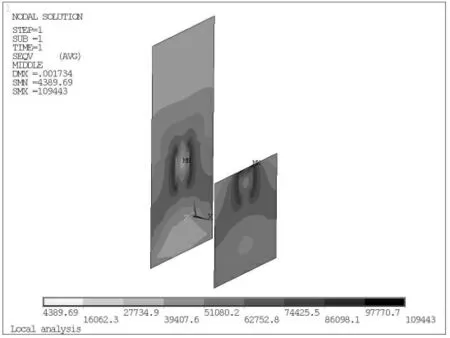
图10 工况4 腹板Mises 应力图

图11 各工况顶板2 及腹板最大Mises 应力曲线

由图9～11 可知，（1） 随着支座加劲板尺寸增大，顶板2 及腹板应力逐渐减小；（2）顶板2 及腹板最大应力均较小， 其应力不作为设计的主要控制因素。

3.4 支座加劲板间距B 对局部受力的影响

根据3.4 节分析，取支座垫板尺寸为h1=450 mm、h2=550 mm 时，不同垫板间距B 情况下的局部受力进行分析。

考虑到支座垫板尺寸为0.7 m×0.7 m， 选定7 个工况进行分析，包括：工况1：B=250 mm；工况2：B=300 mm；工况3：B=350 mm；工况4：B=400 mm；工况5：B=450 mm；工况6：B=500 mm；工况7：B=550 mm。

各工况各板件Mises 应力图同3.4 节给出的各板件应力图相似，各工况下板件最大Mises 应力变化曲线如见12。可见，不同垫板间距B 对结构受力的影响较小，应力变化幅度在10%以内。 因此，对于间距B 的设计仅需考虑制造时的操作空间需求即可。

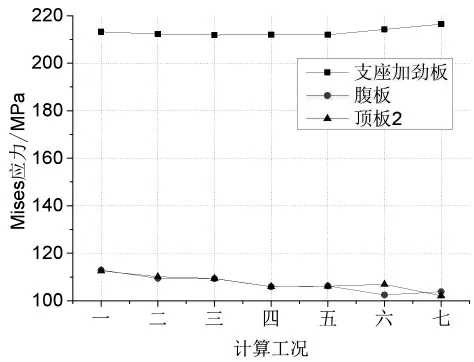
图12 各工况下板件最大Mises 应力曲线

各工况下的稳定系数见图13。 可见，随着垫板间距B 的增大，局部稳定系数缓慢增大，最小稳定系数为7.78，支座部位结构局部稳定性较好。

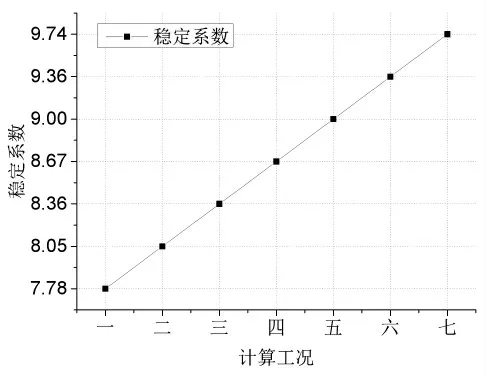
图13 各工况稳定系数

3.5 支座位置局部构件结果分析

根据以上分析，主要结论如下：（1）支座加劲板尺寸可取h1=450 mm、h2=550 mm 作为最合理的设计尺寸；（2）荷载主要由支座垫石边缘开始，由顶板2 和支座加劲板向两侧腹板传递；（3）两侧腹板受力变形引起加劲板底部受拉；（4）加劲板尺寸的增大能把荷载更多地传递给腹板， 减小加劲板受力，同时，也能减小应力集中的数值；（5）支座部位结构局部稳定性较好；（6）顶板2 及腹板最大应力均较小，其应力不作为设计的主要控制因素；（7）加劲板间距B 对板件应力影响小，可仅需考虑制造时的操作空间需求。

4 钢混结合段局部分析

与混凝土盖梁不同，钢盖梁与混凝土立柱交接处的钢混结合段是设计的关键点和难点。 此处板件复杂，且存在钢与混凝土两种不同材料之间的共同受力， 为较好地模拟钢混结合段各板件的受力情况，使用有限元分析软件Ansys 建立钢混结合段局部板壳+实体模型。

4.1 构造拟定

钢混结合段设置于混凝土立柱顶部区域。 参考桥塔钢混结合段的设计方法，钢与混凝土之间采用开孔板连接件形式连接，结合段长度根据开孔板连接件承载力要求， 取为2.6 m （计算方法详见4.4节）。结合段的构造见图14。其中，主要受力板件包括混凝土外包钢板G2、G3， 开孔板连接件KB1、KB1a、KB2、KB2a，角隅处连接件G4、G5，以及相应的加劲板。 板件尺寸和布置根据有限元模型计算确定。

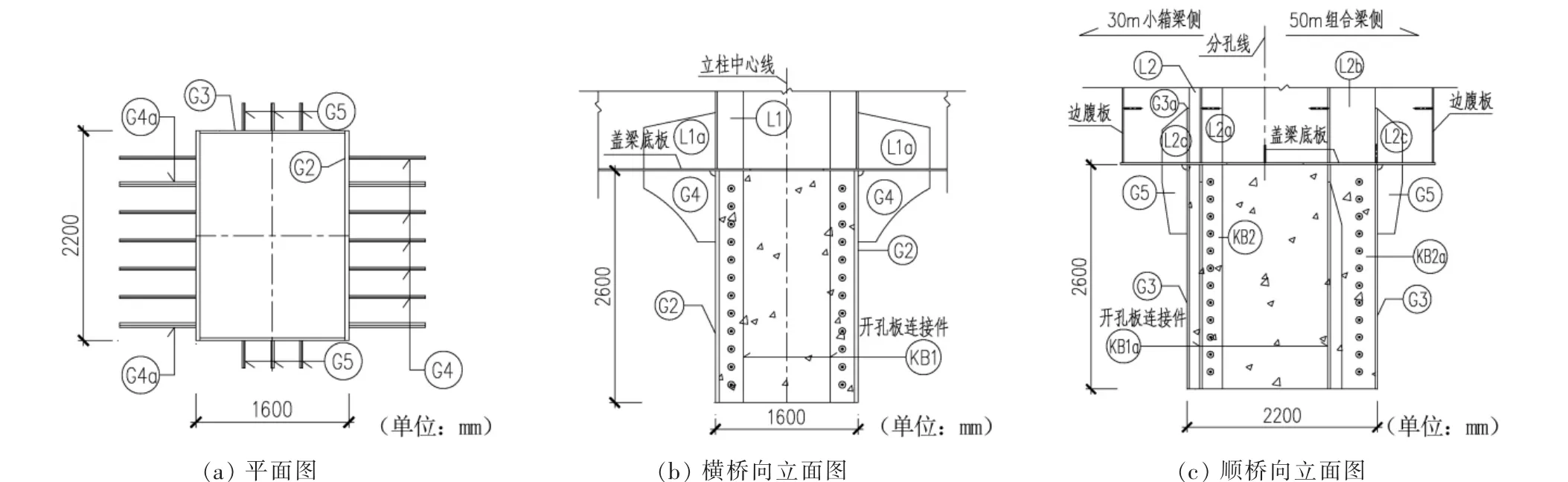
图14 钢混结合段构造图

4.2 有限元模型

4.2.1 计算长度

计算模型应截取桥墩附近局部节段，以避免端部施加集中荷载对连接处的影响。 有限元模型根据隔板位置截取，取节段总长为9.762 m。

4.2.2 计算模型与边界条件

模型采用三维实体-板壳有限元方法计算，其中钢结构用板壳单元（Shell63）模拟，混凝土结构用实体单元（Solid65）模拟，支座垫板采用实体单元（solid95）模拟。 开孔板连接件用非线性虚拟三维弹簧（Combin39）单元模拟。 不考虑焊钉的作用，不考虑钢与混凝土之间的摩擦传力。 有限元模型共计约11 万个单元，11 万个节点（图15)。

图15 钢混连接处有限元模型

4.2.3 边界条件

（1）位移边界条件。 有限元模型中，混凝土桥墩底部固结。G2、G3 板件与混凝土桥墩侧面之间仅约束钢结构板件法线方向的水平约束， 不考虑摩擦。墩顶与盖梁底板之间的考虑接触约束。 开孔板连接件圆孔直径75 mm，孔中贯通钢筋采用HRB400级钢筋，直径30 mm。 开孔板单孔刚度根据《公路钢混组合桥梁设计与施工规范》(JTG/T D64-01-2015)[3]第9.3.2 条计算，可得垂直于钢筋方向刚度为802.4 kN/mm， 平行于钢筋方向连接件刚度为刚性连接。（2）荷载边界条件。除在节段内施加结构自重、二期恒载、上部结构传递的荷载、车辆荷载（根据不同工况对应的荷载和最不利位置施加） 外，还需施加在节段边界处的荷载边界条件。 由Midas 总体计算结果得两工况下力的边界条件，即混凝土墩顶所受最大轴力和最大弯矩两种工况下的节段两侧轴力、剪力和弯矩，作为荷载边界条件。

4.3 应力计算结果

轴力最大工况与弯矩最大工况板件计算结果相似， 本研究仅列出轴力最大工况下各板件Mises应力（图16）。

图16 轴力最大工况板件Mises 应力图

由应力图可知，（1）G4 连接件为最主要的受力构件，将盖梁的变形传递给桥墩；（2）除G4 板件角点位置及内腹板与G4 接触位置出现应力集中外（但超过270 MPa 的范围极小），其余板件应力均较小，可见，板件设计合理。

4.4 稳定计算

稳定系数计算时， 设定稳定系数计算范围为-7～9。 计算结果见表4（负值表示与施加荷载方向相反），节段未出现整体性失稳。 最低阶的稳定系数为6.2845，稳定系数较高，稳定性较好。其中，第8阶为连接处附近失稳，其模态见图17。

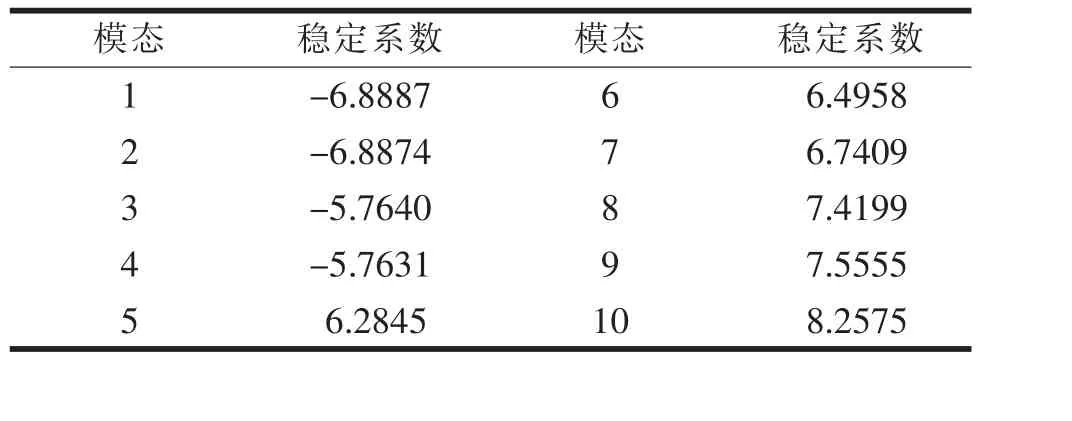
表4 稳定系数表

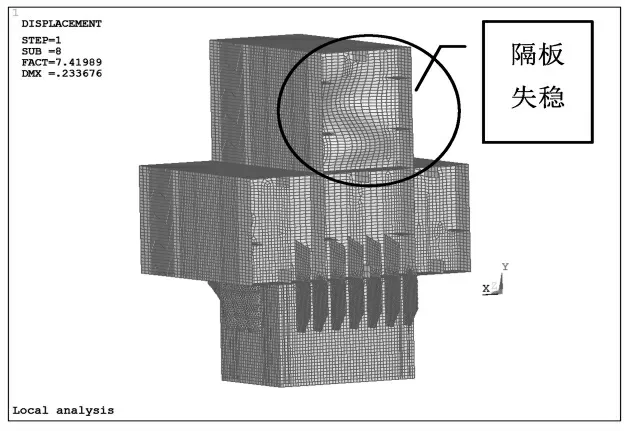
图17 第8 阶失稳模态（连接处附近上隔板）

4.5 开孔板连接件承载能力验算

根据 《公路钢混组合桥梁设计与施工规范》(JTG/T D64-01-2015)[3]第9.3.4 条，开孔板连接件承载能力设计值可按下式计算：

其中，钢筋直径为30 mm，开孔板连接件圆孔直径为75 mm，代入公式可得故开孔板连接件单孔抗剪承载力为478.1 kN。

基本组合下，开孔板连接件单孔最大竖向力发生在开孔板连接件下方位置，为264.57 kN，小于单孔抗剪承载力478.1 kN，开孔板连接件承载力满足规范要求。

4.6 钢混结合段局部分析结果

根据以上分析，主要结论如下：（1）现有设计能满足规范要求；（2）G4 连接件为连接盖梁与桥墩的最主要的受力构件；（3）钢混结合段可通过开孔板连接件进行不同材料之间的传力，但需验算开孔板的承载力；（4）开孔板连接件单孔最大竖向力发生在开孔板连接件下方位置。

5 结论

根据上述分析，针对双柱墩倒T 型钢盖梁的具体设计方法和研究结论如下：（1）倒T 型钢盖梁应进行总体计算和局部分析，支座及钢混连接处分析尤为重要。 （2）支座位置荷载主要通过最近路径传递， 本研究盖梁是由支座垫石边缘开始， 由顶板2和支座加劲板向两侧腹板传递，两侧腹板受力变形引起加劲板底部受拉。 （3）支座加劲板为主要受力构件，应根据实际荷载拟定合理尺寸。 顶板2 及腹板最大应力均较小，其应力不作为设计的主要控制因素。（4）加劲板间距B 对板件应力影响小，可仅需考虑制造时的操作空间需求。 （5）G4 连接件为连接盖梁与桥墩的最主要的受力构件，其尺寸和外形对整体影响大。 （6）钢混结合段可通过开孔板连接件进行不同材料之间的传力，开孔板连接件单孔最大竖向力发生在开孔板连接件下方位置，应根据规范验算开孔板的承载力。

本文通过对倒T 型钢盖梁的总体计算和局部分析，对钢盖梁设计提出了建议。 基于本文的分析方法，可为类似工程提供借鉴和经验。