岩溶区桩基稳定性影响因素数值模拟分析

■尹志芳

（福建省交通规划设计院有限公司，福州 350004）

随着我国高速公路建设和国省道干线改造工程的不断推进，由于建设选线的特殊要求或现有勘探手段有限，桥梁选址难以避免穿越岩溶地区的可能性，岩溶区发育的土洞、溶洞严重威胁桥梁基础安全。 嵌岩桩具有承载力高、群桩效应小、沉降收敛快、抗震性能好的特点，因此是目前岩溶地区桥梁基础设计时的首要选择。 但溶洞跨度、溶洞高跨比对嵌岩桩顶板安全厚度影响如何； 不同嵌岩桩尺寸、嵌岩深度对嵌岩桩承载性能影响如何，目前尚无针对性的研究。 针对以上问题，本文运用FLAC-3D 软件建立研究区典型溶洞和桩基的力学模型，采用有限元方法计算溶洞稳定性并分析其影响因素，以期为研究区实际施工提供理论指导。

1 工程实例概况

连接东肖高速公路与政永高速公路的龙岩南枢纽互通，位于福建省龙岩市新罗区，拟设6 座匝道桥，桥梁总长约1.5 km，总桩基数量300 余根。 互通场区上伏第四系全新统冲洪积层（Q4al+pl），其下为二叠系童子岩组炭质粉砂岩（P1t）、栖霞组灰岩（P1q）及风化层。 该场区岩溶较发育，局部灰岩面上有土洞发育，岩溶、土洞部分有充填，部分无充填，最小埋深5.8 m， 最大埋深92.6 m， 溶洞垂高以0.4～10.8 m 为主，个别可达到24.9～27.7 m，如表1 所示。

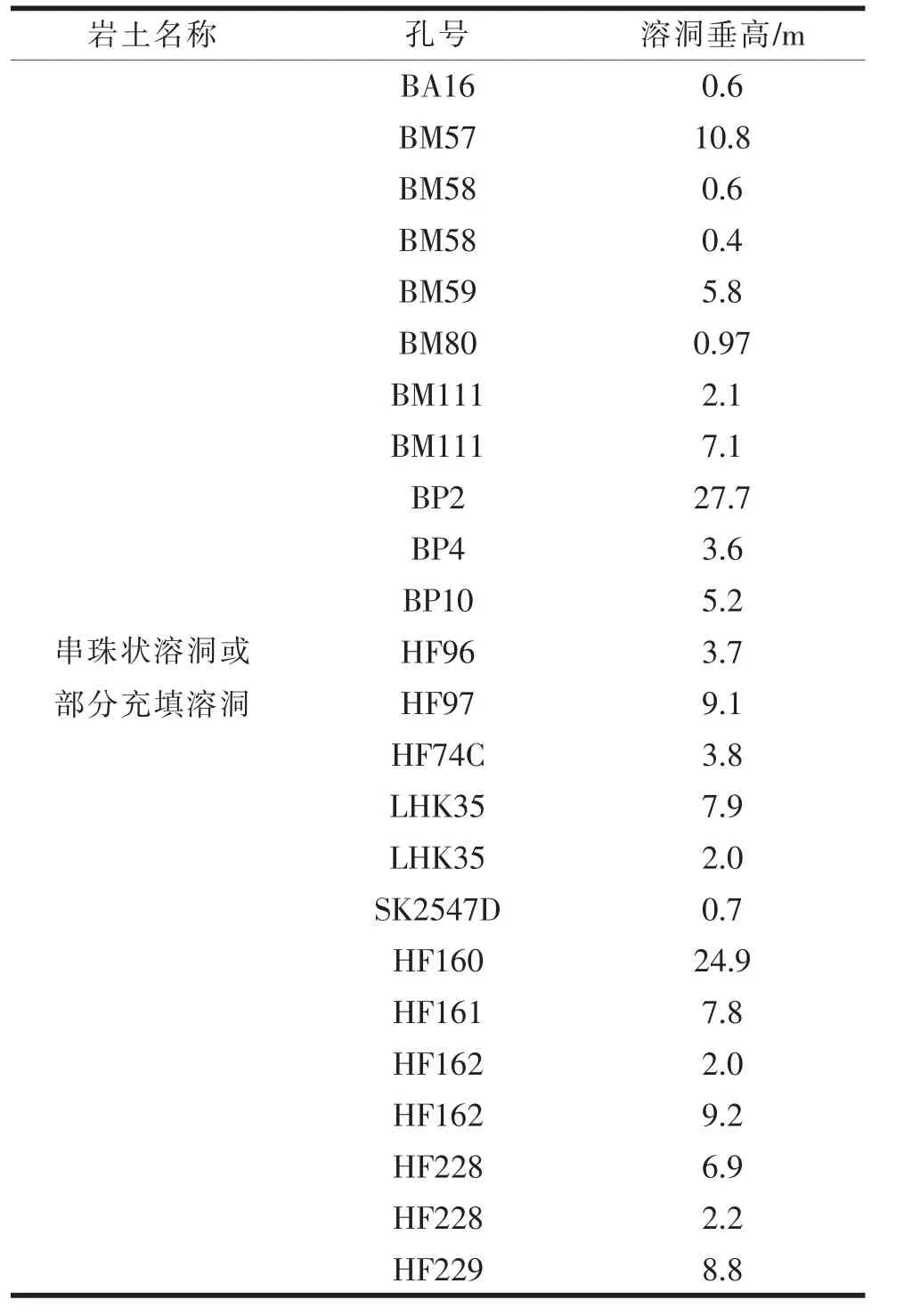
表1 互通区溶洞特征

2 桩基溶洞稳定性模拟基础

2.1 FLAC-3D 软件简介

FLAC-3D 软件即连续介质快速拉格朗日差分分析软件，具有强大的计算处理功能，可以通过不同初始单元模型组合、连接建立三维工程地质模型来模拟岩溶区溶洞结构位移及受力情况[1]。

2.2 计算模型及参数指标的选取

本次数值模拟分析在龙岩南枢纽互通岩溶发育原型的基础上进行适当的简化，并假设溶洞周边岩体是理想的各向均等的，岩土体的物理力学参数指标主要根据试验成果，并结合当地类似工程可靠经验进行适当调整， 采用摩尔-库仑 （Mohr-Coulomb）屈服准则，通过ANSYS 进行数据转换处理后导入FLAC-3D 软件生成溶洞模型。

由表1 可知，溶洞平均垂高值为6.7 m，大部分数值在2～11 m，占总数的75%左右，结合场区经验及模型的建立，综合考虑选取溶洞垂高值分别为3、5、7、9、11 m；按照类球形或方形溶洞计算，所选溶洞计算宽度及高度在3～11 m。 根据互通区典型钻孔揭露的地层资料、试验成果及历史经验，场区土层、灰岩及桩体的参数取值如表2 所示。

表2 土层、灰岩及桩体的参数取值

2.3 桩基荷载、桩径及嵌岩深度的选取

根据施工现场收集的工程资料分析，现场嵌岩桩桩基成孔工艺主要为人工挖孔灌注桩或冲孔灌注桩[4]，单桩承载力特征值一般为6000～18000 kN，桩径范围一般为0.6～2.0 m， 本文采用的计算模型选取桩径为2.0 m 进行计算分析。 岩溶地区的桩基嵌岩深度的选择，现行规范尚未统一，根据《公路桥涵地基与基础设计规范》第9.4.4 条要求[5]，在满足最小嵌岩深度要求的条件下，应尽量减小基桩嵌岩深度，以保证溶洞顶板完整性。 因岩溶区发育程度差异较大，且岩面起伏不定，实际施工中一般要求嵌岩深度不宜小于1.0 m；同时考虑经济合理性，最大嵌岩深度一般不大于2 倍桩径，基于以上考虑且为方便计算，本次数值模拟分析嵌岩深度取值分别为1、2、3、4 m。

2.4 模型基本参数

FLAC 模型基本参数如下：5 级加载：6000～18000 kN；桩径：2 m；桩长：55 m；嵌岩深度：1～4 m；跨度：2～6 m；模拟范围从地表到溶洞发育区下伏较完整的中风化～微风化灰岩， 一般取地下55 m 左右。 桩侧土层分为两层，上层为含角砾粘土层，厚度为25～30 m，下层为5～10 m 厚的碎卵层。

2.5 模拟范围及边界条件

溶洞的几何形状对顶板的稳定性及极限承载力有一定的影响，结合工程实际情况，溶洞形态一般可分为两类：一类为因地下水抬升或下降潜蚀形成的类球形；另一类为受地下暗河冲刷而形成的长通道形。 为简化计算，本次模拟计算采用球形和方形溶洞模型进行对比分析，以找出实际工程中更危险的溶洞形态。

为提高计算的精确性并尽量使计算接近实际情况，本次数值模拟计算采用摩尔-库仑本构模型，取桩基影响宽度为20 m，桩长为55 m。考虑到研究区溶洞平均垂高为6.7 m，取球形溶洞直径为7 m，方形溶洞尺寸为7 m×7 m×7 m，桩径取2 m，桩底距顶板为4 m， 分5 级（6000、9000、12000、15000、18000 kN）逐级加载。

在嵌岩桩顶施加初级荷载为6000 kN 时，对比分析球形溶洞与方形溶洞的数值模拟结果（图1、2）可知，球形溶洞顶板的塑性区域明显小于方形溶洞顶板的塑性区域范围，表明方形溶洞在荷载的作用下受到应力集中的影响，在相同荷载下更易产生塑性变形。 出于安全考虑，在后文的计算中均采用方形溶洞模型进行数值模拟分析。

图1 球形溶洞顶板塑性区域（桩顶荷载6000 kN）

图2 方形溶洞顶板塑性区域（桩顶荷载6000 kN）

3 模拟结果分析

按前述取方形溶洞尺寸为7 m×7 m×7 m，嵌岩桩径取2 m， 桩底距顶板为4 m， 分5 级（6000、9000、12000、15000、18000 kN）逐级加载，模拟分析计算得出的桩基及溶洞顶板竖向应力、位移及顶板塑性区域分布范围如图3～5 所示。

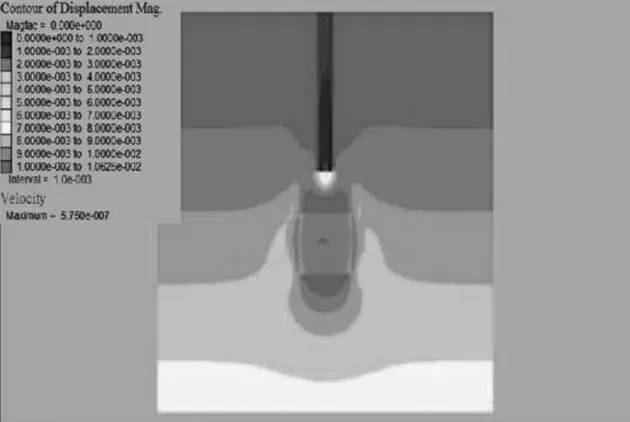
图3 桩基及溶洞顶板的竖直方向应力图

由图3～5 结果分析可知，本次数值模拟分析的嵌岩桩桩顶在竖向集中荷载作用下，桩底及溶洞周边岩体应力、 应变范围均未超出模拟的边界范围，可知本次模拟计算边界条件的选取有效，分析结果可靠。

3.1 位移与应力分析

（1）由图3 模拟结果可知，因桩体强度明显高于桩周岩土层，在桩端底部与溶洞顶板之间形成了应力集中现象；并且受溶洞形状影响，在方形溶洞的四角也大体产生了应力集中现象。 （2）由图4 模拟结果可知，受桩侧土层摩阻力的影响，桩侧位移明显比桩端以下基础范围内的位移更小；而嵌岩桩桩端直接作用在变形模量较大的中风化灰岩上，明显造成桩端以下溶洞顶板位移小于桩顶位移。 由图3 所示的溶洞周边应力分布结果可知，溶洞顶板位移将呈现出两侧小中间大的趋势， 从而形成图4所示的铃铛形或钟形。 （3）由图5 模拟结果可知，嵌岩桩桩端下岩体已产生了塑性应力并形成了塑性变形， 但与溶洞顶板上部岩体的塑性区域尚未连通，由此可以判定此时溶洞顶板处于极限应力平衡的稳定状态。

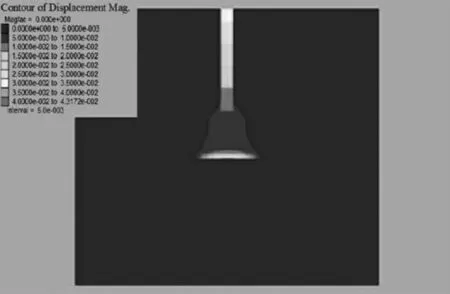
图4 桩基及溶洞顶板的竖向位移

图5 溶洞顶板塑性区域

3.2 影响溶洞顶板安全厚度的单因素分析

3.2.1 溶洞跨度因素影响分析

按照摩尔-库仑模型计算本构模型， 选取参数如表2 所示，方形溶洞尺寸为7 m×7 m×7 m，溶洞位于桩端底面中心下4 m 处。 当桩顶荷载设置为设计荷载的6000 kN 时， 此时溶洞及四周形成了如图5 所示的类似的塑性区域，而溶洞顶板处只出现了小范围的塑性变形， 同样未与嵌岩桩端底面贯通。 一般情况下小范围的塑性变形并不影响溶洞顶板整体稳定性， 此时溶洞顶板仍处于基本稳定状态。 但当桩顶荷载超过设计荷载，达到9000 kN 时，溶洞顶板的塑性区域范围已明显扩大，并与嵌岩桩端底面连通，判定此时溶洞顶板已经处于易产生溶洞塌陷或造成桩基失稳的状态。

结合上述模拟分析结果，考虑到现场实际情况可能与模型选取的参数指标存在一定差异，同时考虑桥梁属该互通区的重要构筑物，桩基设计时安全度水准应适当提高，故溶洞顶板在极限平衡下的厚度应乘以一个安全系数。 根据工程经验，建议安全系数取值在1.05～1.25；当溶洞跨度较小时（小于或等于3 m），则取安全系数取值1.05；当溶洞跨度较大时（大于或等于11 m），则安全系数取值1.25；其它溶洞跨度下安全系数采用线性插值法确定。 根据选取的计算模型，溶洞跨度为7 m，则安全系数值应为1.15，溶洞顶板安全厚度应为4.6 m。

由此分别对3～11 m 的溶洞跨度进行数值分析， 计算其相对应的顶板安全厚度及厚跨比，结果如表3 所示。 由表3 可知，溶洞顶板安全厚度随溶洞跨度增大而增大，但增大幅度是逐渐收敛的，即顶板安全厚度与跨度比值随溶洞跨度增大而减小。

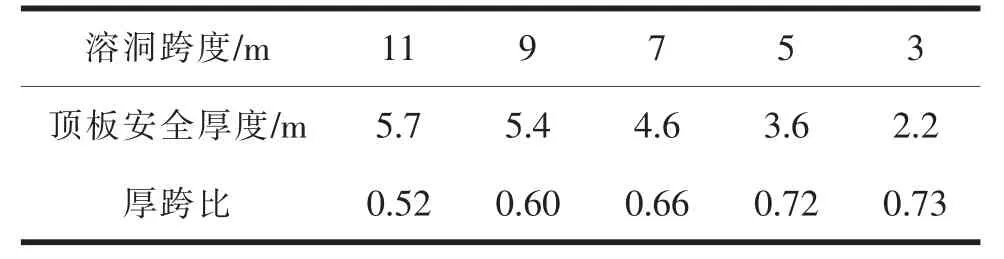
表3 溶洞跨度与顶板安全厚度计算结果

3.2.2 溶洞高跨比因素影响分析

前述模拟采用的模型均是在理想的方形溶洞情况下（即溶洞高跨比为1 时），计算的顶板安全厚度。但工程实际也有大部分溶洞高跨比并不等于1，为此取溶洞顶板跨度为固定值9 m， 溶洞高度取值范围为3～11 m， 桩顶荷载为6000 kN 进行数值模拟分析不同溶洞高度、 相同跨度下的应力分布，结果如图6～8 所示。

图6 溶洞顶板塑性区域（高度3 m）

图7 溶洞顶板塑性区域（高度7 m）

图8 溶洞顶板塑性区域（高度11 m）

由图6～8 可知，当取溶洞顶板的跨度为固定值时，溶洞高跨比与溶洞顶板安全厚度呈反比。 这是由于当溶洞高度较小时，高跨比小于1，此时溶洞呈水平向扁平状，上部荷载传递到溶洞顶板时，上覆压力基本全部由顶板承担，即形成所谓的应力集中现象；当溶洞高度逐渐增大时，高跨比大于或等于1，此时溶洞呈方体状或竖向条块状，上部荷载局部由溶洞侧壁承担，即形成所谓的应力扩散现象。

3.2.3 桩径尺寸因素影响分析

仍按照前述的摩尔-库仑模型计算本构模型，竖向桩顶荷载取固定值6000 kN， 桩径取值范围为0.6～2.0 m，进行模拟分析计算，得出相应的溶洞顶板安全厚度，并以安全厚度为纵轴，以桩径尺寸为横轴，按最小二乘法进行拟合计算分析，得出两者关系如图9 所示。

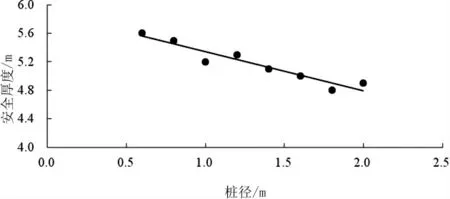
图9 桩径与安全厚度的关系

从图9 显然可以看出，在桩顶荷载远大于桩身自重时，桩径尺寸越大，桩底面积越大，受应力扩散影响，溶洞顶板上覆应力越小，溶洞稳定性越高，则顶板安全厚度越小。 但当桩径增大到一定时，桩身自重已增大到足够影响溶洞顶板应力分布，此时桩径继续增大，溶洞顶板压力仍将持续减小，但减小幅度是逐渐收敛的，相应的溶洞顶板安全厚度减小幅度也是收敛的。

3.2.4 嵌岩深度因素影响分析

根据近20 余年嵌岩桩工程和试验研究积累的相关资料，参考《建筑桩基技术规范》(JGJ 94-2008)[6]中嵌岩桩极限承载力计算公式和条文说明，嵌岩桩端阻分担荷载比随嵌岩深径比增大而减小，也就是说，由于嵌岩段岩层桩侧摩阻力的存在，桩顶荷载传递到溶洞顶板的附加应力会随着嵌岩深度的增加而减小。

取嵌岩深度分别为1、2、3、4 m， 桩顶荷载设置为9000 kN，按程序软件进行数值模拟，得到桩体周围及溶洞顶板塑性区域分布如图10～13 所示。

图10 溶洞顶板塑性区（嵌岩1 m，桩顶荷载9000 kN）

由图10～12 可知，随着嵌岩深度的增加，桩体和溶洞顶板的塑性区域逐渐减小，所需的溶洞顶板安全厚度也是逐渐减小的。 但当嵌岩深度超过3 m后（图12～13），塑性区域并没有明显减小，由此说明，嵌岩深度值和所需的溶洞顶板安全厚度值并不是持续成反比的， 存在一个最适宜的安全厚度值，按照本文的计算模型和实际工程情况，一般取嵌岩桩直径的1.2～1.5 倍比较经济合理。

图11 溶洞顶板塑性区（嵌岩2 m，桩顶荷载9000 kN）

图12 溶洞顶板塑性区（嵌岩3 m，桩顶荷载9000 kN）

图13 溶洞顶板塑性区（嵌岩4 m，桩顶荷载9000 kN）

4 结论

本文在龙岩地区龙岩南互通桥梁桩基原型的基础上进行一定的简化和理想化处理，运用FLAC-3D 软件进行分析计算时，模拟范围以地表为上界，以溶洞发育区下较完整的中风化灰岩为下界；位移约束边界采用约束模型四周及底部的位移值，地面为自由边界，对溶洞桩基进行位移分析并计算了单因素影响下顶板的安全厚度。 主要结论如下：（1）由位移分析可知，受桩侧土层摩阻力的影响，溶洞顶板位移将呈现出两侧小中间大的铃铛形或钟形。 （2）溶洞顶板安全厚度随溶洞跨度增大而增大，但增大幅度是逐渐收敛的，即顶板安全厚度与跨度比值随溶洞跨度增大而减小。 （3）当溶洞顶板的跨度一定时， 溶洞顶板安全厚度随溶洞高度的增加而递减，由此可以得出溶洞高跨比与溶洞顶板安全厚度呈反比。 （4）一般而言，桩径尺寸越大，桩底面积越大，受应力扩散影响，溶洞顶板上覆应力越小，则溶洞稳定性越高，则顶板安全厚度越小。 但桩径增大到一定时，桩身自重已增大到足够影响到溶洞顶板应力分布，此时桩径继续增大，溶洞顶板压力仍将持续减小，但减小幅度是逐渐收敛的，相应的溶洞顶板安全厚度减小幅度也是收敛的。 （5）随着嵌岩深度的增加， 桩体和溶洞顶板的塑性区域逐渐减小，所需的溶洞顶板安全厚度也是逐渐减小的，但嵌岩深度值和所需的溶洞顶板安全厚度值并不是持续成反比， 按照本文的计算模型和实际工程情况，一般取嵌岩桩直径的1.2～1.5 倍比较经济合理。

5 结语

本文所建立的数值分析模型虽然以龙岩地区龙岩南互通桥梁桩基为原型，但不可避免仍经过一定的简化处理。 互通区实际岩溶发育程度差异较大，上部土层起伏变化大，并不是如模型所示的均匀分布，实际下伏的中风化灰岩受层理和节理裂隙影响存在应力分布不均匀等情况，可能会造成模拟分析计算结果与实际情况有一定出入，但这并不妨碍对岩溶区桩基溶洞稳定性影响因素数值模拟研究的方法探讨。 在实际运用中，可以根据现场施工及运营期的实际情况，充分收集后期检测监测数据成果后进行对比分析，对数据参数及边界条件进行修正，建立更符合现场实际地质情况的数值分析模型，从而得到更接近实际工况的结论，为其他类似工程设计和施工提供借鉴。