基于小波分析的长江南京段分级水位研究

于慧 仲跻文 李强 蔡璇 蔡磊 肖仲凯

摘要：为研究长江南京段高低潮水位的分级等问题，采用Mann-Kendall检验、复Morlet小波分析法分析了南京潮水位站1950～2020年潮水位的变化趋势、周期。采用滑动平均序列提取趋势项法量化潮位的变化趋势，对南京潮水位站的年最高、最低潮位进行修正。采用频率分析方法推求对应频率90%下的高水位、50%下的中水位及10%下的低水位。计算思路及成果为长江南京段高低潮水位的分级研究、生态水位及水资源的保护利用等提供一定的科学依据。结果表明：南京潮水位站年均潮水位变化趋势不明显，年最高潮水位、年最低潮水位序列存在明显的增加趋势;年均潮水位、年最高潮水位、年最低潮水位周期为10，15，14 a，且南京潮水位站年最高潮、最低水位序列的次周期均同为9 a，年最高潮水位与年最低潮水位的变化波动尺度比较接近。

关键词：潮水位;趋势;小波分析;一致性修正;长江南京段

中图法分类号：P332 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2021.12.006

文章编号：1006 - 0081（2021）12 - 0038 - 06

0 引 言

传统的工程水文计算理论和方法以不变概率分布为假定，然而近期由于人类活动和气候变化的双重影响，不同时期的水文要素发生了一定程度的渐进性变化，导致实测水文资料的一致性不满足计算要求，因此在采用频率分析方法推求设计潮位之前，需要对水文要素序列进行修正。

本文考虑多年来径流来水变化、天文气象变化、河床边界条件以及大型水利工程运行等人类活动的综合影响，将南京潮水位站1950～2020年水位资料作为研究对象，采用多种水文分析方法，系统完整地研究了南京潮水位站1950～2020年潮水位的趋势和周期。本文采用小波分析周期修正方法对南京潮水位站1950～2020年年最高潮位序列、年最低潮位序列进行了序列修正，采用年特征值频率分析法确定了高、中、低水位级标准。研究成果对深入认识长江南京段潮水位年际变化规律、水位等级划分等具有一定意义，可为长江南京段防洪管理、生态水位等提供一定依据。

1 研究背景

长江下游河段上起九江（锁江楼）下迄江阴鹅鼻嘴。下游部分河段受海洋潮汐影响，水位每日两涨两落，就平均情况而言，潮区界在大通附近，负流界在南京附近[1]，潮流界在江阴至镇江附近，南京至江阴段潮汐影响较为明显，长江南京段河道示意如图1所示。

2 分析方法

2.1 趋势分析方法

本文趋势性分析方法采用Mann-Kendall[3]检验法（简称M-K检验）和Spearman[4]秩次相关系数法。采用M-K检验法分析南京潮水位站特征水位序列的趋势性。Mann-Kendall检验法是世界气象组织推荐并已广泛使用的非参数检验方法，最初由Mann和Kendall提出。M-K检验不需要样本遵从一定的分布，也不受少数异常值的干扰，适用于水文、气象等非正态分布的数据。

原假设H0序列未发生趋势变化。采用如下统计量：

[S=i=1n-1j=i+1nsign（xj-xi）] （1）

式中：[sign（xj-xi）=1，xj-xi>00，xj-xi=0-1，xj-xi<0]

当N ≥ 10时，统计量近似服从正态分布，其标准化后的量由下式计算：

[Z=（S-1）/N（N-1）（2N+5）/18，S>00，         S=0（S+1）/N（N-1）（2N+5）/18，S<0] （2）

式中：N為序列长度，在给定的显著性水平[α]下，查标准正态分布表，可做出接受或拒绝H0的判断。若[Z>0]，则认为有上升趋势;若[Z<0]，则认为有下降趋势;若[Z>Uα2]，则认为序列存在明显的趋势变化。

采用Spearman秩次相关系数法检验时间序列的趋势性，统计检验用的秩相关系数按下式计算：

[Rs=1-6i=1Nd2i/（N3-N）]  （3）

[di=Xi-Yi]                         （4）

式中： [Xi]为周期1～N按水位值从小到大排列序号;[Yi]为按时间排列的序号;[di]为变量[Xi]和变量[Yi]的差值;N为周期数，本文以年为周期。

构造统计量[T]如下：

[T=Rs（N-41-Rs2）0.5]              （5）

统计量[T]服从自由度为[（N-2）]的[t]分布，若[T]小于0，则序列呈上升趋势，若[T]大于0，则序列呈下降趋势。根据给定的显著性水平[α]，可查出[ta2]。如果[T>ta2]，则序列随时间有相依关系，从而推断序列趋势明显，[T]越大，在一定程度上可以说明序列的趋势性变化越显著;[T<ta2]，序列趋势不显著。

2.2 周期分析方法

本文周期分析采用小波分析[5]。小波分析是一种时、频多分辨率分析方法，具有时频局部化功能，可以对函数和信号系列进行多尺度细化分析，以分析不同尺度（周期）随时间的演变情况。小波分析能将水文时间系列的频率特征在时间域上展现出来，分析出其主要周期[6]。

对于给定的小波函数[ψ（t）]（本文选用复Morlet小波，形式为： [ψ（t）=eicte-t2/2]，时间序列[f（kΔt）]的离散小波变换系数[Wf（a， b）]为

[Wf（a，b）=a-12Δtk=1Nf（kΔt）ψ（kΔt-ba）]     （6）

式中：[a]为尺度因子，反映小波的周期长度;[b]为时间因子，反映时间上的平移。

将时间域上关于[a]的所有小波变换系数的平方进行积分，即为小波方差

[Var（a）=-∞∞Wf（a，b）2db]               （7）

小波方差随尺度[a]的变化过程称为小波方差图，通过小波方差图，可以确定一个水文序列中存在的主要时间尺度，即主周期。

2.3 潮位序列的一致性修正方法

水文时间序列[Z（t）]，一般由趋势项[A（t）]、周期项[P（t）]和随机项[R（t）]组成，表达式为：

Z（t）=A（t）+P（t）+R（t）                  （8）

实测潮位序列由趋势项、周期项和随机项综合组成，直接对实测序列提取的趋势项，很可能受到周期项和随机项的干扰[7]。本文基于小波分析的主周期为长度，推求实测序列Z（t）的滑动平均序列Zma（t），则Zma（t）中周期变化可使序列的随机波动得以部分抵消，在一定程度上克服随机波动的影响，所以对滑动平均序列Zma（t）提取趋势项A（t），可有效避开序列周期变化和随机波动的干扰。采用最小二乘法将趋势项[A（t）]从时间序列中分离出来，则已知[A（t）]，[t]=1，2，…，[n]，而一致性修正的目的正是要消除序列中的趋势项，因此潮位序列可按下式修正至现状水平[8]：

[Z（t）=Z（t）+[A（n）-A（t）]]，[t]=1，2，…，[n]     （9）

式中：[Z（t）]为修正后潮位;[Z（t）]为实测潮位;[A（n）]为序列第[n]项（现状水平年）的趋势值;[A（t）]为序列第[t]项的趋势值。

趋势项[A（t）]可用多项式描述，即：

[A（t）=a0+a1t+a2t2+]…[+aktk]           （10）

式中：[k]为多项式阶次;[aj]（[j]=0，1，2，…，[k]）为待定系数。

2.4 潮位分级划分方法

本文采用年特征值频率分析法[9]划分高、中、低水位级标准。具体步骤如下。

以频率分析计算作为水位级划分的基本依据，频率可计算为

[P=mn+1×100%]                      （11）

式中：P为频率，%;m为排队位数;n为数据序列数。

选取南京潮水位站1950～2020年的年最高潮水位、年最低潮水位和年均潮水位这3个序列作频率分析计算，分别得到[Zmax-P]，[Zmin-P]及[Zm-P]三条频率曲线。在这3条曲线中分别截取P=90%的[Zmax]为高水位，P=10%的[Zmin]为低水位，P=50%的[Zm]为中水位，借以划分水位级。

3 南京潮水位分级

3.1 趋势性分析

根据南京潮水位站1950～2020年实测潮水位资料，南京潮水位站1950～2020年多年平均潮水位为5.30 m，年均潮水位最大值出現在1954年，为6.65 m，年均潮水位最小值出现在2011年，为4.41 m;年最高潮水位最大值为2020年的10.39 m、年最低潮水位的最小值为1956年的1.54 m。

表1为南京潮水位站特征水位统计表。从表中统计数据可知：20世纪50时代是长江南京段高水期，而后进入低水期，枯水期持续到20世纪70年代末，从80年代初至2002年，长江南京段又进入高水期。2003年后长江南京段进入低水期。年最高水位在60年代较低，60年代后呈增加趋势，在2003至2020年有所回落;而年最低水位在年代统计值呈增加趋势，在2003年后尤其明显[10]。

图2为南京潮水位站特征水位逐年变化图，从图2可以看出， 年平均水位变化比较平缓，线性趋势不明显;而年最高水位、年最低水位的线性趋势均呈现一定的增加趋势，但其趋势的显著性有待检验。

上述时间序列的趋势是依据序列数据线性趋势性判定的，其趋势的显著性需要进一步的检验。表2为南京潮水位站1950～2020年特征水位序列趋势性检验统计表。在[α=0.05]的显著水平上，由检验结果可知：①年均潮水位序列基本无变化趋势;②年最高潮水位和年最低潮水位序列呈现明显的增加趋势，其趋势性通过[α=0.05]的显著性检验。

3.2 周期分析

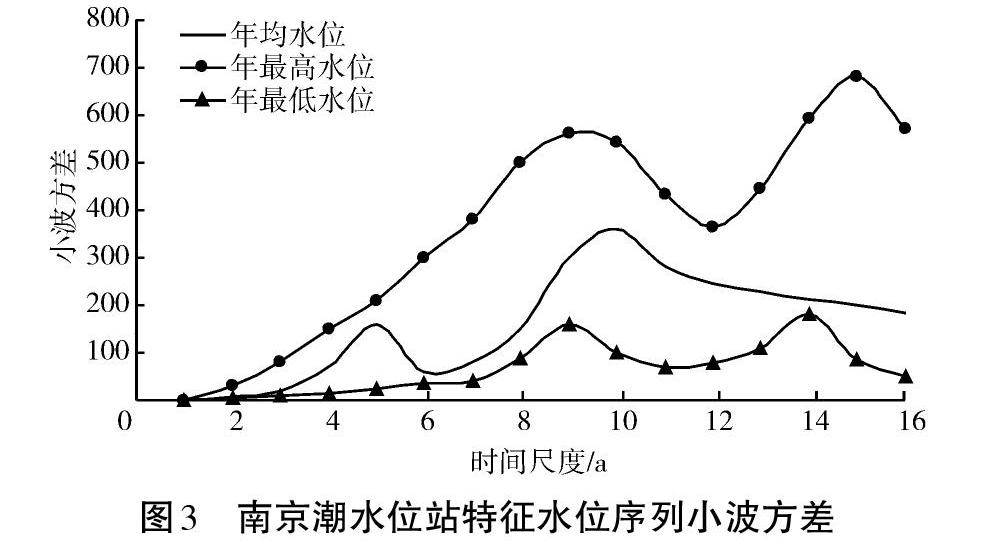
图3为南京潮水位站1950～2020年特征水位序列小波方差图，小波方差反映波动的能量随尺度的分布，小波方差图的峰值为序列存在的主要时间尺度。表3为对应的分析序列的主周期（最高峰）和次周期（次高峰）。由图2及表3可知：①南京潮水位站年均潮水位序列的主次周期为10 a和5 a;②南京潮水位站年最高潮水位序列的主次周期为15 a和9 a;③南京潮水位站年最低潮水位序列的主次周期为14 a和9 a。

南京潮水位站年均潮水位10 a主周期与中国近百年来降水7～14 a的长周期对应[11]。长江南京段潮水位的主要影响因素有径流来水变化、海洋潮汐变化、河床边界条件以及大型水利工程运行等人类活动。对于长江南京段年最高潮水位和年最低潮水位，海洋潮汐的影响同样很重要，由潮汐理论知，受月球的影响，外海潮汐具有18.6 a的长周期[12-14]，但外海的潮波在进入长江口以后，由于地形、径流的影响会发生变形，其周期与天然径流周期相互作用后介于二者之间[15]。

3.3 潮位序列的一致性修正

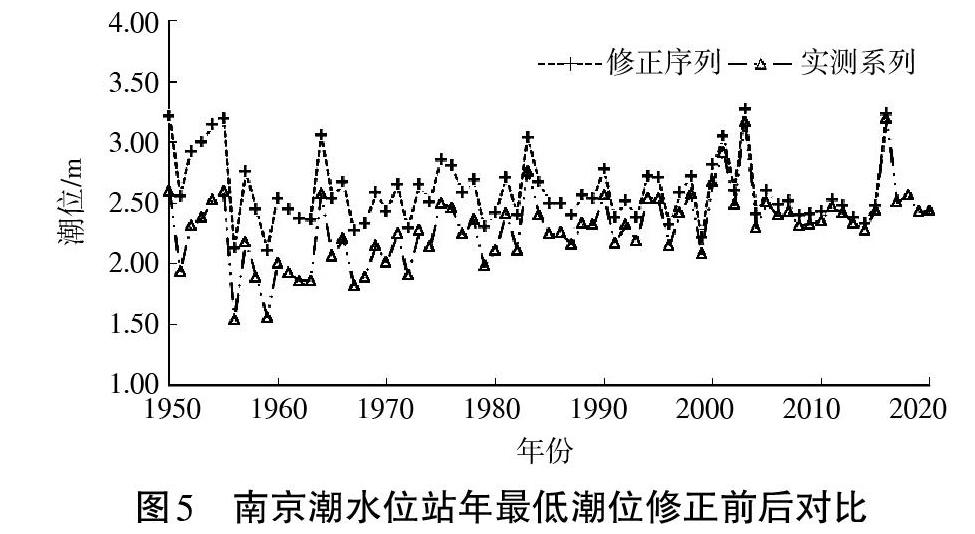
本文采用滑动平均序列提取趋势项法量化潮位的变化趋势，基于前文分析的南京潮水位站年最高潮、最低水位序列的次周期均为9 a的结论，对南京潮水位站的年最高、最低潮位序列求9 a滑动平均，所得滑动平均序列与实测序列相比首尾各少4项。对滑动平均序列，采用最小二乘法确定趋势项中的待定系数[a0]，[a1]和[a2]，得南京潮水位站的年最高、最低潮位滑动平均序列的趋势项，以滑动平均序列确定的趋势项为基础，对南京潮水位站的年最高、最低潮位进行修正。

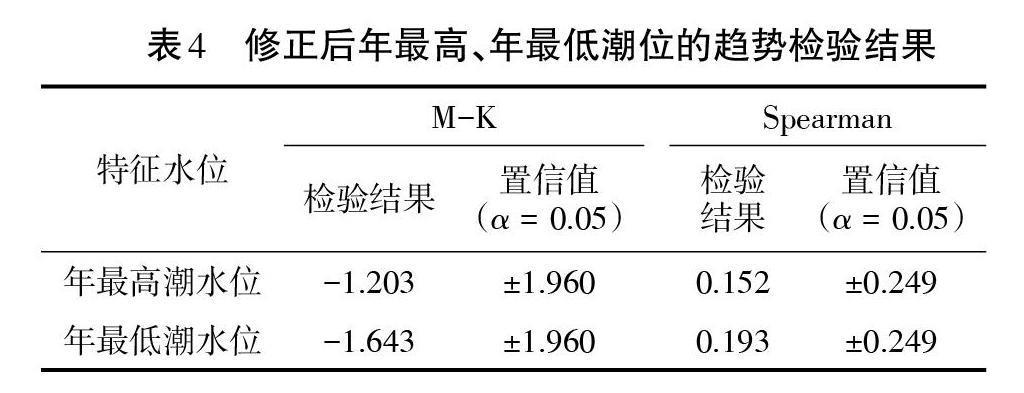
通过对南京潮水位站的年最高、最低潮位实测序列求滑动平均，可使序列的随机波动得以部分抵消，在一定程度上克服随机波动的影响，可见图4和图5。对南京潮水位站年最高、年最低潮位修正序列进行Mann-Kendall检验和Spearman秩次相关系数法检验，结果列于表4。由检验结果可知修正后的年最低潮位序列满足独立同分布条件[16]。

3.4 潮位分级划分计算

根据GB 50179-2015《河道流量测验规范》规定：对于一类精度的水文站，水位级的划分可采用年特征值法，并应符合下列规定：①根据测站各年瞬时最高水位[Zmax]，计算频率和绘制频率曲线，当频率P为90% 时，其对应的水位，为高水位;②根据测站各年瞬时最低水位[Zmin]，计算频率和绘制频率曲线，当频率P为10% 时，其对应的水位，为低水位;③根据测站各年日平均水位[Zm] 計算频率和绘制频率曲线，当频率P为50% 时，其对应的水位为中水位。

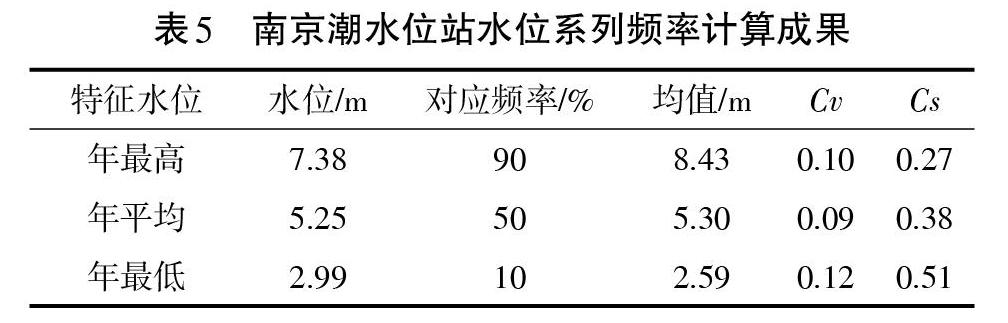
本文采用南京潮水位站1950～2020年修正后年最高水位系列，采用频率分析方法推求对应频率90%下的高水位;依据南京潮水位站1950～2020年实测年平均水位系列，采用频率分析方法推求对应频率50%下的中水位;依据南京潮水位站1950～2020年修正后年最低水位系列，采用频率分析方法推求对应频率10%下的低水位。

采用数学期望公式计算样本的经验频率、选择P-Ⅲ线型为各序列的总体分布线型、通过计算机适线确定参数，对年最高水位、年平均水位、年最低水位3个序列进行频率计算，结果见表5，频率曲线图见图6。

4 结 语

（1）本文采用多种水文分析方法研究了南京潮水位站1950～2020年年均潮位、年最高水位、年最低水位序列的趋势性、周期结果表明：年均潮位序列变化趋势不显著，而年最高潮位、年最低潮位序列呈现明显的增加趋势。

（2）基于小波分析的3个潮位序列周期，对年最高、最低潮位序列进行了系列修正，对修正后的潮位序列再作趋势性检验，结果表明：潮位趋势性变化不再显著，说明对潮位数据的一致性修正达到了预期的效果。根据修正后的潮位序列数据继而进行了潮位分级划分计算。本文分析计算思路及成果可为长江南京段高低潮水位的分级研究、防洪规划、生态水位及水资源的保护利用等提供一定依据。

参考文献：

[1] 邹振华，李琼芳，夏自强，等. 人类活动对长江径流量特性的影响[J]. 河海大学学报（自然科学版），2007（6）：622-626.

[2] 陈钢，程和琴. 长江下游河道河床阻力分布特征及影响因素分析[J]. 长江科学院院报，2019，36（8）：10-16.

[3] 秦年秀，姜彤，许崇育. 长江流域径流趋势变化及突变分析[J]. 长江流域资源与环境. 2005，14（5）：589-594.

[4] 王盼成，贺松林. 长江大通站水沙过程的基本特征I. 径流过程分析[J]. 华东师范大学学报（自然科学版）. 2004（2）：72-80.

[5] 王文圣，丁晶，李跃清. 水文小波分析[M]. 北京：化学工业出版社，2005.

[6] 韦立新，于慧，汪周园，等. 鄱阳湖入江径流变化规律及成因分析[J]. 人民长江，2014，45（23）：88-91，97.

[7] 肖淼元，李国芳，王伟杰.  长江口潮位一致性检验与修正方法研究[J].  长江科学院院报，2013，30（4）： 6-10.

[8] 姚思源，李国芳，钱睿智，等. 南水北调东线工程源头长江潮位预报[J/OL]. 南水北调与水利科技（中英文）：1-12[2021-08-09]. http：//kns.cnki.net/kcms/detail/13.1430.TV.20210729.1721.006.html.

[9] 董胜，廖振焜，焦春硕. 乘潮水位估计的逐时潮位统计法[J]. 水运工程，2018（1）：29-34.

[10] 张景瑞，季小梅，张蔚，等. 三峡工程对长江下游感潮河段极值水位的影响[J]. 水道港口，2021，42（1）：78-83.

[11] 严华生，万云霞，邓自旺，等. 用正交小波分析近百年来中国降水气候变化[J]. 大气科学，2004，28（1）：151-157.

[12] HAO Y，LU J. Teleconnection between climate oscillations and riverine nutrient dynamics in Southeast China based on wavelet analysis. [J].  Environmental science and pollution research international，2021.

[13] 庄圆，纪棋严，左军成，等. 海平面上升对中国沿海地区极值水位重现期的影响[J]. 海洋科学进展，2021，39（1）：20-29.

[14] 解朝娣，吴小平，雷兴林，等. 长周期潮汐与全球地震能量释放[J]. 地球物理学报，2013，56（10）：3425-3433.

[15] 魯盛，吴志龙，童朝锋. 基于实测资料的长江口潮波演变规律研究[J]. 人民长江，2019，50（9）：86-93.

[16] 周宏，李卫东，欧淑芳，等. 滁河中下游暴雨与长江潮位频率组合分析[J]. 人民长江，2016，47（14）：36-39，63.

（编辑：李 晗）

Research on graded water level of Nanjing section of Yangtze River based on wavelet analysis

YU Hui， ZHONG Jiwen， LI Qiang， CAI Xuan， CAI Lei， XIAO Zhongkai

（Lower Changjiang River Bureau of Hydrological and Water Resources Survey， Bureau of Hydrology ， Changjiang Water Resources Commission， Nanjing 210011， China）

Abstract： In order to classify the high and low tide levels in the Nanjing section of the Yangtze River， Mann-Kendall test and complex Morlet wavelet analysis were used to analyze the trend and cycle of the tide level at the Nanjing tide station from 1950 to 2020. The moving average sequence is used to extract the trend item to quantify the trend of the tide level， and the annual maximum and minimum tide levels of the Nanjing tide level station are corrected. The frequency analysis method is used to calculate the high water level at 90% frequency， the medium water level at 50% frequency， and the low water level at 10% frequency . The calculation ideas and results can provide a certain scientific basis for the classification study of the high and low tide water levels of the Nanjing. The analysis showed that the annual average tidal level change trend at Nanjing tide water level station is not obvious， and the annual highest tide water level and the annual lowest tide water level sequence have an obvious increasing trend; the annual average tidal water level， annual highest tide water level， and annual lowest tide water level cycle are 10 years ， 15 years， 14 years， and the sub-periods of the annual highest tide and lowest water level sequence at the Nanjing tide water level station are all 9 years， and the fluctuation scales of the annual highest tide water level and the annual lowest tide water level are relatively close.  Section of the Yangtze River， the ecological water level and the protection and utilization of water resources.

Key words：  tide level; trend; wavelet analysis; consistency correction;Nanjing section of the Yangtze River