壤中暴雨流机制耦合遥感地表蒸散量在山洪模型中的应用

王濂 王力 张革联 匡威 张艳军

摘要：山区小流域产汇流模式的研究成果较少，且现有模型计算精度不高。对山洪产汇流机理进行了研究，初步确定山洪过程的主要产流方式是壤中暴雨流机制。进行了山洪模拟模型的比选和研发，根据壤中暴雨流机制具备对洪水进行调蓄的功能，提出从微观角度对壤中流进行分析，進一步做Boussinesq假设，发展了基于壤中暴雨流机制的山洪模拟模型。将模型应用于云南省清水河流域的洪水模拟，结果表明，与传统方法相比，本方法的计算结果的精度提高显著。

关键词：壤中暴雨流;遥感地表蒸散量;TOPMODEL模型;DTVGM模型

中图法分类号：P426.62 文献标志码：A DOI：10.15974/j.cnki.slsdkb.2021.12.001

文章编号：1006 - 0081（2021）12 - 0008 - 08

1 研究背景

水文过程模型作为流域水文模型的基础，一直推动着水文模型的发展，该类模型包括：坡面产流模型、汇流模型以及河道汇流模型[1]。坡面产流模型是在19世纪后期开始发展，并随着霍顿（Horton）《地表径流现象》的发表开始取得重大突破。20世纪60年代开始，在大量野外观测的基础上，Dunne等[2]发现：除超渗产流外还存在另一种产流机制——蓄满产流。而以赵人俊为代表的学者通过大量实验发现，在湿润地区主要发生蓄满产流，而在干旱地区主要是超渗产流。在1972年，Kirkby[3]等进一步推动了产流机制的研究，使对产流的认识更为深入。

目前，对于山区小流域产汇流模式的研究成果较少，除了传统的产汇流理论外，较为经典的一个理论是壤中暴雨流理论。根据Dingman[4]的定义，壤中暴雨流（Subsurface Storm Flow）是壤中流（Subsurface Flow）的一种，也称壤中水径流[5]、暴雨快速壤中流或快速壤中流[6]。壤中暴雨流主要指在降水过程中，由于山坡表层透水性很强，降雨会快速下渗并蓄积在相对不透水层或者土壤-基岩界面上，形成了土壤暂态饱和区，进而产生饱和（或近饱和）侧向流动现象。区别于水体在土壤非饱和区的流动。

在比较上百个不同流域的研究成果后，Mirus等[7]总结了湿润山区小流域产流模式的重要特点：径流主要来源于壤中暴雨流，传统的饱和地表径流（Saturation Overland Flow）和超渗地表径流（Hortonian Overland Flow）占河道径流的比重很小。这也是山区小流域的场次洪水洪量和降水量相关性低，经常出现“降雨大、洪量小”或“降雨小、洪量大”现象的原因之一。根据Mirus对蓄满产流机制的总结改进，壤中暴雨流通常发生在土壤-基岩界面上，是湿润、陡峭、植被覆盖良好山区的主要产流机制，也是山区流域径流的最主要组成部分。

基岩地形和土壤深度对壤中暴雨流的存储、运动和出流具有重要的影响。在陡坡，土壤较薄层和土壤下渗率大于降雨量的区域，水流垂直移动到深层处，在土壤-基岩界面上或在相对不透水层上形成暂态饱和区，然后往侧向较低处移动。降雨期间暂态饱和流主要在基岩上运移，因此，相较地表地形而言，基岩地形更直接地控制着水流的方向和存储[8]。自“国际水文十年计划”（IHD）以来，壤中暴雨流对降水的非线性响应研究也取得一定进展，尽管壤中暴雨流是山区流域产流的最重要控制因素，但由于其机理复杂，数据难以获取，集成该产流机制的水文模型十分困难且稀少。

壤中暴雨流机制具备对洪水进行调蓄的功能，本文提出了从微观的角度对壤中流进行分析，进一步做Boussinesq假设。考虑到地表上层土壤含水量对土壤蒸发的不同响应和深层根区土壤含水量对植被蒸腾的不同响应，模型首先将土壤-植被系统的净辐射分为土壤和植被两部分，分别考虑了直接短波辐射和漫射短波辐射的传输以及长波辐射通过林冠的传输，然后，利用土壤和植被净辐射的差异，计算出土壤/植被的4个干/湿端元，最后根据两相ET动力学和4个端元温度将土壤蒸发和植被蒸腾分离[9]。加入双源遥感地表蒸散量估算方法，为模型的构建提供理论基础，模拟结果精度大幅显著提高，具有很强的鲁棒性。

2 研究方法与基础资料

2.1 研究方法

对于流域降雨径流特征的分析以及对该流域洪水过程的模拟，应该采用壤中暴雨流机制[10]。而该机制应具备对洪水进行调蓄的功能，且随着土壤含水量的增加，壤中暴雨流流速增加，即当饱和含水层厚度较小时，即使降雨量很大，壤中暴雨流流速依然很小;反之，当饱和含水层厚度较大时，即使降雨量很小，壤中暴雨流流速却很大[11]。假设坡长为L，土壤厚度为D（基岩深），即

[V1-V2Δt=iL-q2-q12] （1）

式中：V1，V2为不同暂态下单宽饱和区可排放水的体积，m2;q1，q2为不同暂态下单宽排水率，m2/s;i为非饱和区向饱和区的输水速度，m/s。

在此基础上，假设在该土壤单元上饱和土壤水水面存在一恒定的坡度，且该水力坡度等于基岩的坡度，于是有：

[V=H0ωdL/2q=H0Kssinα] （2）

当饱和地下水面抬升到土壤表面后，该式可为

[V=DωdL+Ls/2q=DKssinα+iLs] （3）

式中：[H0]为饱和地下水厚度，m;α为基岩坡度;[ωd]为土壤有效孔隙度;[Ls]为饱和坡长，m;[Ks]为饱和渗透系数，m/s。

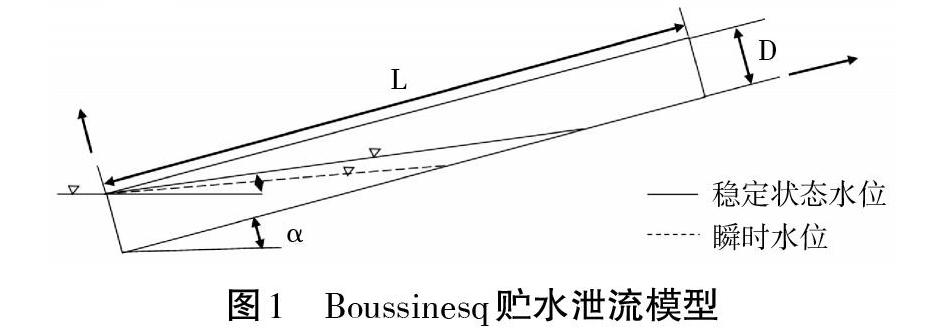
在这个模型的基础上，进一步做Boussinesq假设（图1），即：饱和土壤水面的坡度是恒定的，且等于水力坡度。模型结构如图1所示，于是有：

[V=D2ωd2tanα-βq=H0Kssinβ] （4）

当饱和地下水面抬升到土壤表面后，该式可为

[V=LDωdD-tanα-β2q=i+DKssinβ] （5）

式中：β为自由水面坡度，即水力坡度。

对该公式进行分析，假设该土壤单元的基岩坡度α、山坡坡度β、土壤孔隙度ωd以及饱和渗透系数Ks等是稳定的，即土壤性质及形状不变，随着降雨的不断发生，土壤中饱和地下水厚度在不断上升，此时壤中暴雨流的单宽排水率在不断变大，且该排水率与饱和地下水厚度成正比。当地下水饱和后，速度发生一个突变，并且稳定。

由图2可知，当饱和地下水厚度较小时，壤中暴雨流流速较小，此时q小于非饱和区排水速率i，研究单元处于蓄水状态。此时会出现“降雨大而流量小”，甚至长时间测不到洪水的情况;当达到一定蓄水量时，q大于i，研究单元开始泄水，且流速不断变大。此时会出现“降雨小而流量大”的情况，整个过程与壤中暴雨流机制完全吻合，可以用来对其进行模拟。

2.2 1973～1987年洪水模拟计算

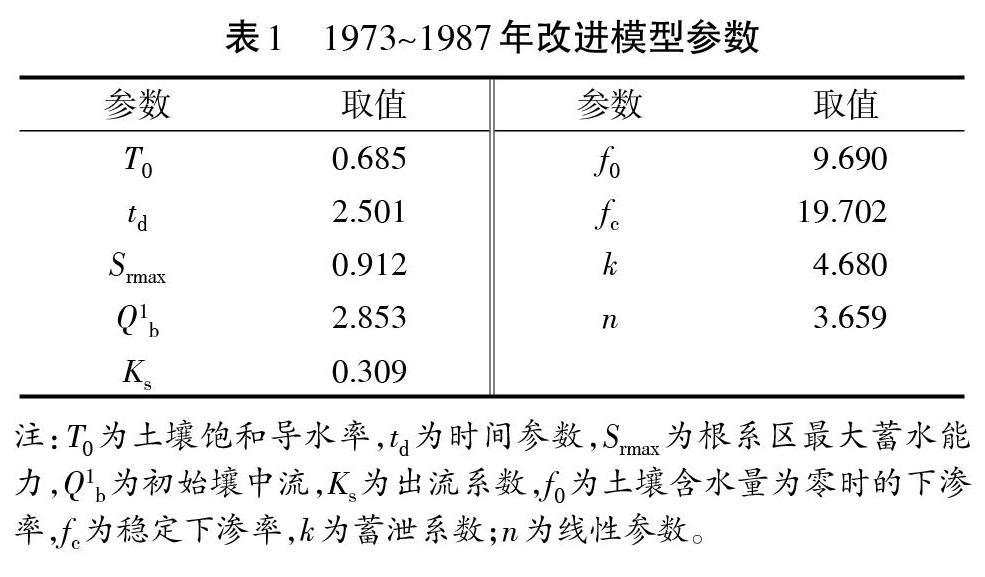
使用基于壤中暴雨流机制及双源遥感地表蒸散量估算方法的山洪模拟模型，以清水河流域（位于云南省红河哈尼族彝族自治州红河县，属于元江水系，是元江右岸的一级支流）1973～1987年的降雨径流数据进行模型参数的率定与检验，结果见表1。

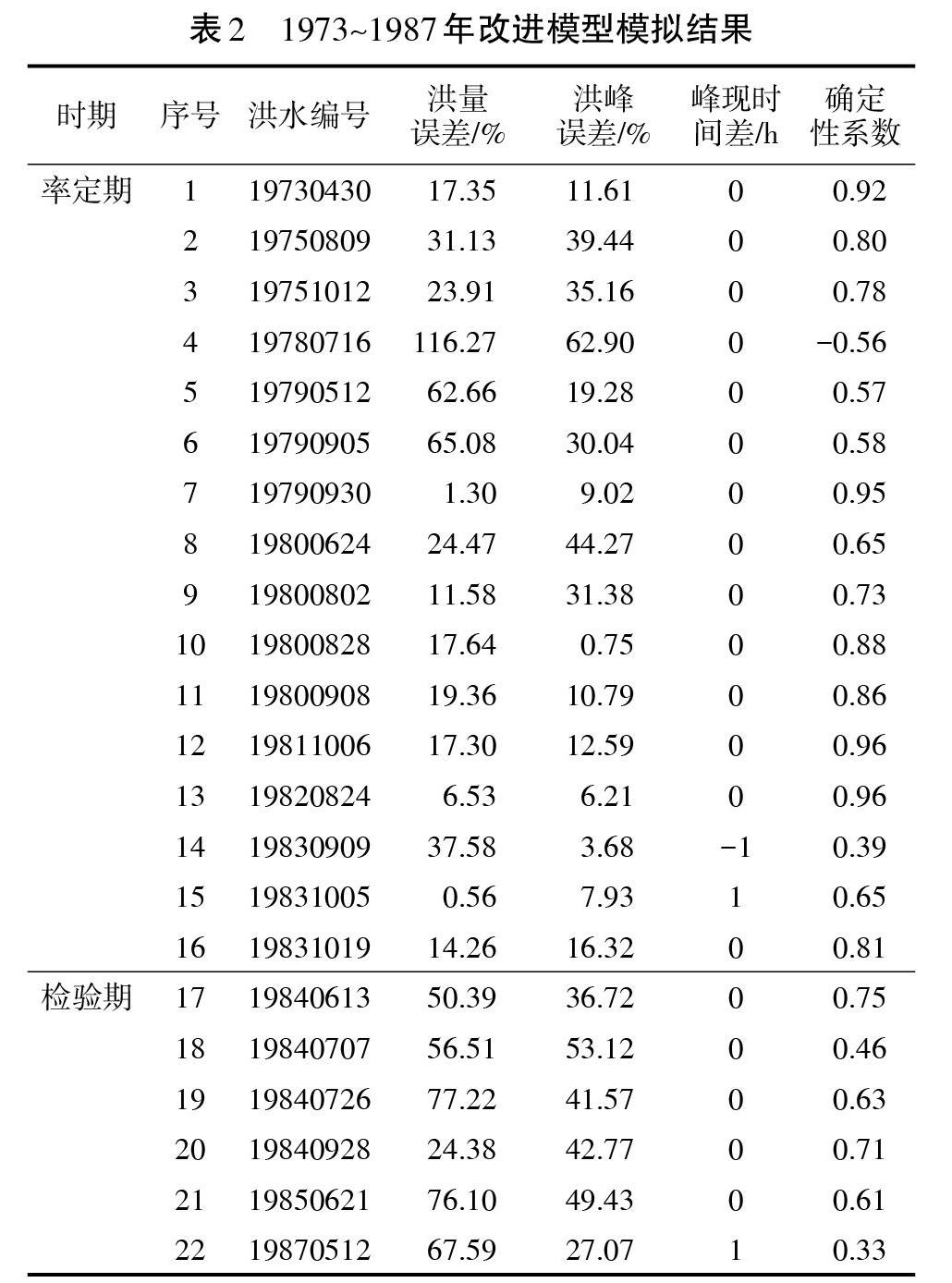
对率定期与检验期的运行结果进行统计，结果见表2。使用改进模型对该流域1973～1987年的洪水进行模拟，其中，包括率定期场次洪水16场，检验期6场。

率定期结果的总确定性系数为0.74，而检验期的确定性系数为0.69。除去一场负值，各场次确定性系数的变化范围为0.39～0.96。从具体各场次的洪水模拟结果来看，率定期效果普遍好于检验期。根据水文情报规范，若以确定性系数为评价标准，合格的模拟次数为16次，合格率为72.7%，预报精度为乙等。其中，有4场洪水模拟的确定性系数大于0.9，说明模拟的洪水过程与实际的洪水过程很接近。

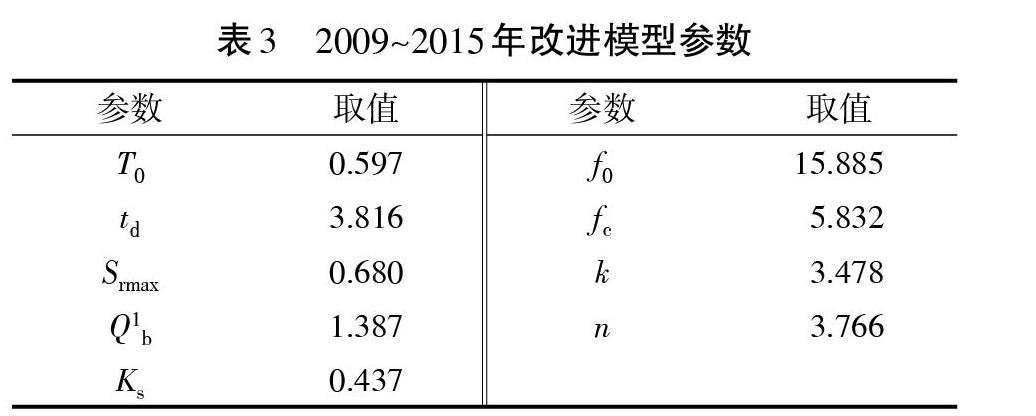
对于洪量误差以及洪峰误差，两者的误差范围跨度较大，最小洪量误差仅为0.56%，而最大的洪量误差有116.27%;最小洪峰误差0.75%，而最大洪峰误差为62.90%。就具体场次洪水来看，若以20%为限制标准进行评价，合格有8场，合格率为36.4%，模拟精度较低。仔细观察发现，这8场合格的洪水模拟均在率定期。这表明，就洪量以及洪峰误差而言，这套参数模拟效果较好，但是预报精度很差。峰现时间的模拟结果精度同样较高，22场预报的峰现误差均在一个计算时段内，合格率100%。使用改进模型以及该流域2009～2015年的降雨径流数据进行模型参数的率定与检验，结果见表3。

2.3 2009～2015年洪水模拟计算

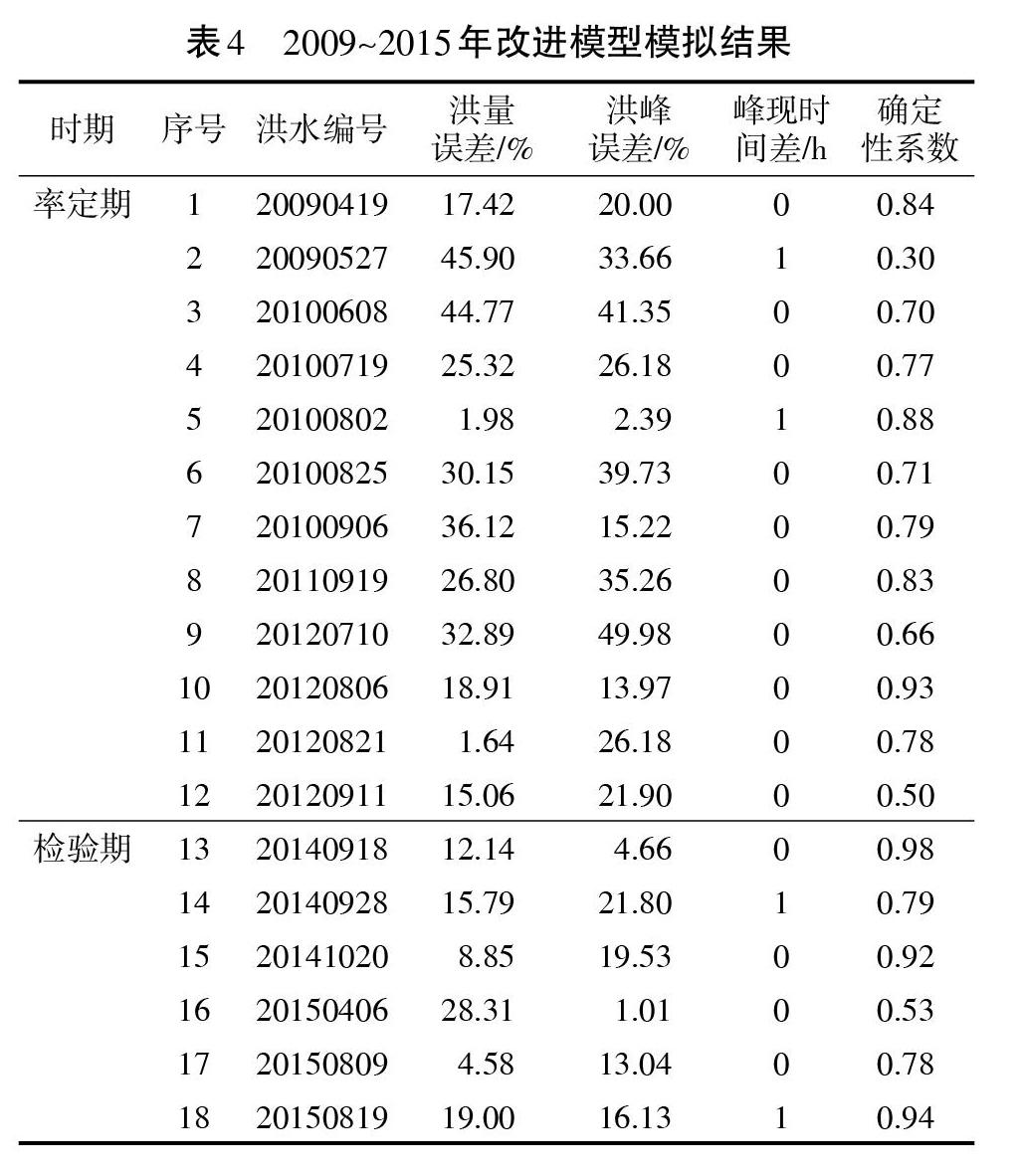
使用基于壤中暴雨流机制及双源遥感地表蒸散量估算方法的TOPMODEL模型，对清水河流域2009～2015年洪水进行模拟，包括率定期洪水12场，检验期6场（见表4）。

对于确定性系数，率定期结果的总确定性系数为0.84，检验期的总确定性系数为0.80，此次模拟与预报的各场次洪水的确定性系数均为正值，最大确定性系数为0.98。从具体各场次的洪水模拟与预报的结果来看，率定期与检验期的效果均较好。根据水文情报规范，以确定性系数为评价标准，合格的模拟次数有14次，合格率达77.8%，精度达到乙级，而检验期6场洪水中有3场洪水确定性系数达到0.9以上，预报效果较好，基本达到预期目标。

对于洪量以及洪峰误差，模拟结果一般，平均的洪量误差以及洪峰误差在23%左右。若以20%为限制标准进行评价，合格的模拟仅有7场。但是，相较于传统模型的模拟结果，模拟精度已经有所提升。对于峰现时间的模拟，18场预报的峰现误差均在1个计算时段内，合格率100%。

3 结果与讨论

对比分析上述两次模拟结果，基于壤中暴雨流机制及双源遥感地表蒸散量估算方法的TOPMODEL模型，应用于该流域的模拟效果有以下几个特点：

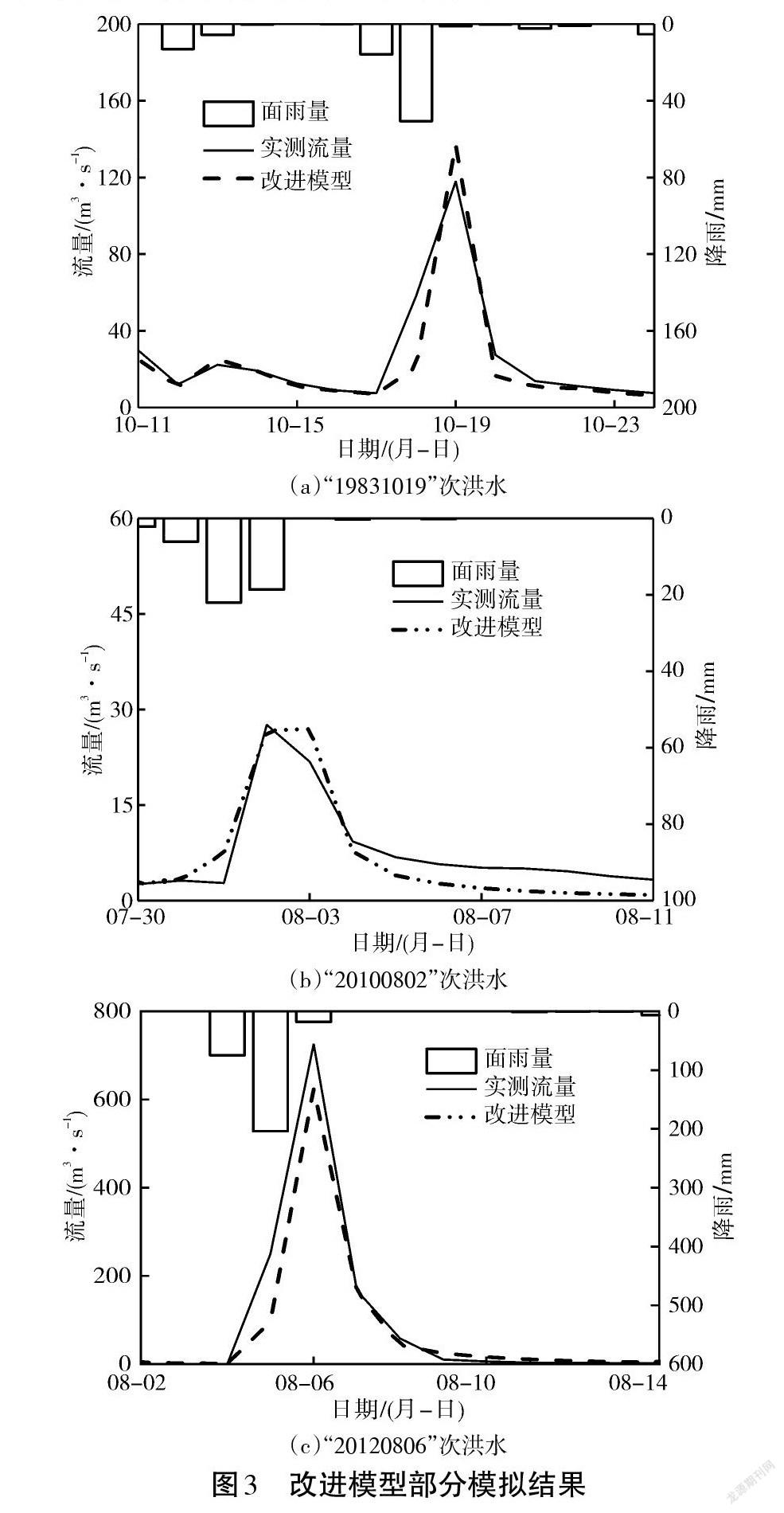
（1）从总体模拟效果看，使用改进的TOPMODEL模型对清水河流域进行洪水模拟的效果较好，比如洪号为“19831019”次洪水，该次洪水确定性系数为0.81;洪号为“20100802”以及“20120806”次洪水，相应的确定性系数分别是0.88和0.93（图3）。同时，2009～2015年检验期的确定性系数为0.80，说明预报精度较高，基本达到预期目标。

（2） 不同的前期气候条件下，模型的适用性均较好。比如洪号“19730430”以及“20140918”次洪水，洪水过程分别见图4。前期流域持续降雨，土壤含水量较高，产流机制偏向于蓄满产流。两次模拟的确定性系数分别为0.92和0.98，模拟精度较高。

对于洪号“20150819”次洪水，洪水过程见图4（c），该次洪水前期流域降雨较少，而且突然降雨，降雨量达75.1 mm。而且从实测的洪水过程来看，洪水陡涨陡落，且洪峰形状对称性好，此时产流机制更偏向于超渗产流，基于壤中暴雨流改进的模型模拟结果确定性系数为0.94，模拟效果较好。

（3）改进后的模型模拟部分场次的洪峰流量比实际流量偏低。改进的模型除了增加壤中暴雨流过程，也增加了植被截留过程，加强了调蓄作用，使降落在流域的水量减少，故洪峰流量下降。比如洪号“20120821”次洪水，洪水过程见图5。由图5可知，模拟的洪峰流量小于实测流量。

4 改进前后模型对比

将传统模型与改进模型的模拟结果绘于同一张图进行对比分析，部分的場次洪水模拟结果对比见图6。通过对比分析，可以得到以下几点结论：

（1） 与传统TOPMODEL模型相比，含有壤中暴雨流机制及双源遥感地表蒸散量估算方法的TOPMODEL模型对于洪峰的模拟更接近于实测洪峰流量值。如洪号“20140918”“20141020”“19831005”以及“19850505”次洪水，洪水过程见图6。由图6可知，改进的TOPMODEL模型模拟的洪峰和洪量与实测流量过程更加接近。这是增加了壤中暴雨流机制及双源遥感地表蒸散量估算方法结构的结果。改进的模型使用实测的基岩深度代替传统模型中的非饱和区最大蓄水深度。此时，下渗到土壤中的水量与实际情况更为接近，径流的主要来源变为壤中暴雨流。而土壤中的径流过程与坡面径流过程差异较大，这种情况下，传统的蓄满产流模型模拟的效果会出现偏差，改进模型模拟的洪水过程与实际情况更为接近。

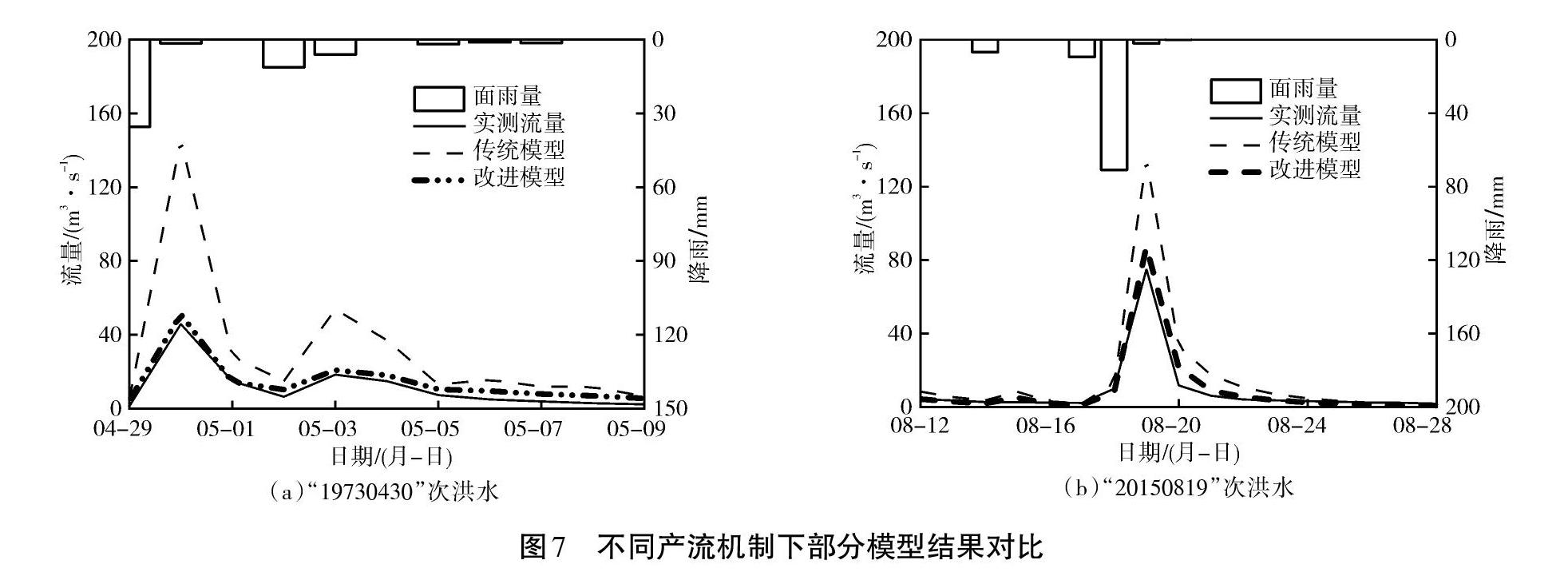
（2）含有壤中暴雨流机制及双源遥感地表蒸散量估算方法的TOPMODEL模型对不同的产流机制適应性更强。比如“19730430”以及前述“20150819”次洪水，洪水过程见图7。这些场次洪水很可能发生超渗产流。传统模型洪峰流量的模拟值与实测流量偏差较大，模拟精度较差，但改进后的模型模拟结果与实测流量过程拟合较好。

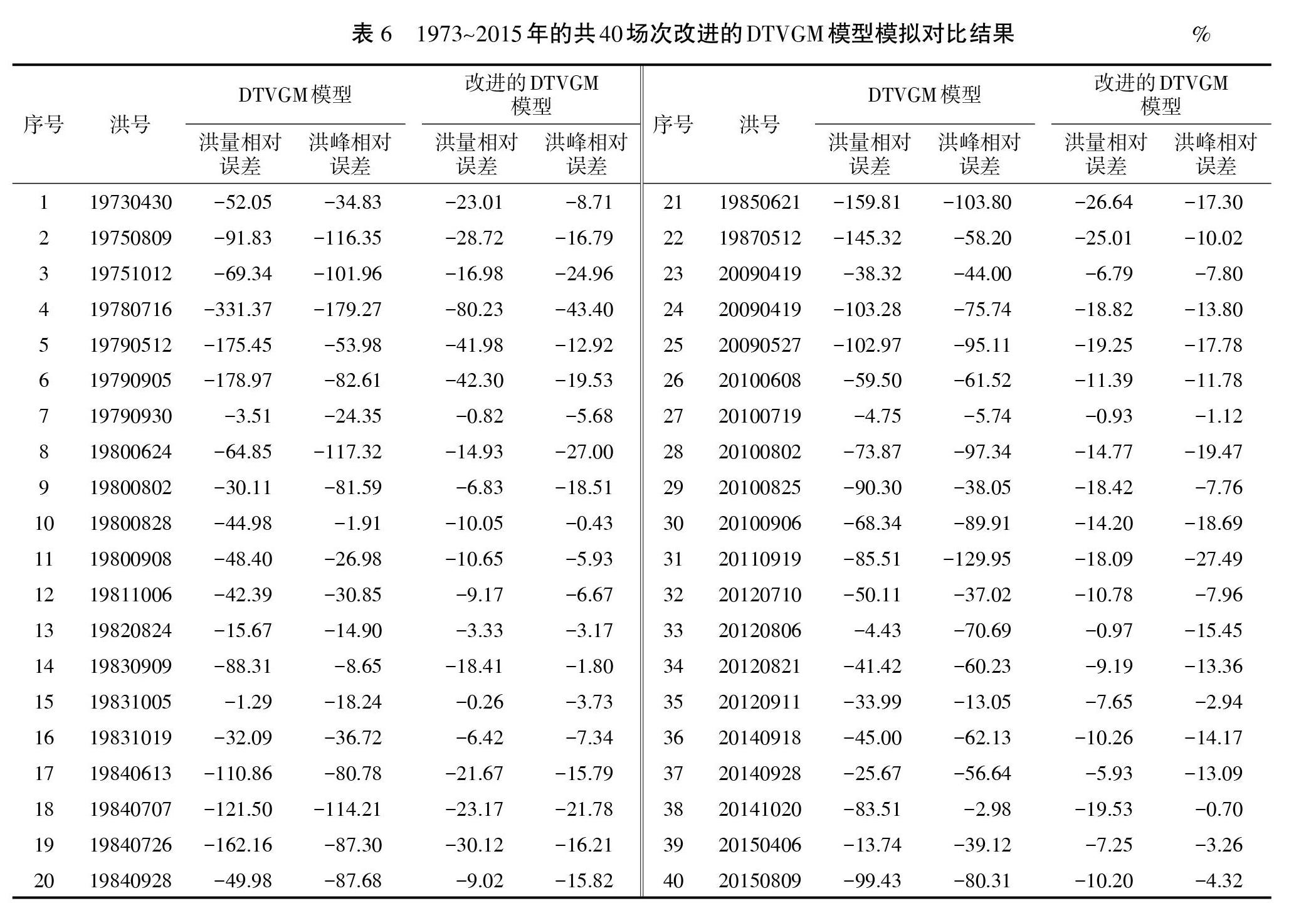
分别对1973～2015年的共40场次洪水的改进模型对比分析，包括半分布的改进TOPMODEL模型和集总式的改进DTVGM模型，基于壤中暴雨流机制及双源遥感地表蒸散量估算方法，配合雷达定量估测降水方法（QPE），对模型改进前后的洪量相对误差和洪峰相对误差进行了对比分析，见表5～6。

分析结果表明，改进后的半分布TOPMODEL模型和改进后的集总式DTVGM模拟结果精度均大幅显著提高。后续工作中，可继续融合云计算技术，加强壤中暴雨流机制及双源遥感地表蒸散量估算方法在不同地区的应用研究。

5 结论与展望

根据研究流域地形地势复杂等特点，选择多种模型进行改进，对其结构以及相关计算方程进行修正，增加了壤中暴雨流机制特征，并加入双源遥感地表蒸散量估算方法，为模型的构建提供理论基础。选用TOPMODEL模型和DTVGM模型对清水河流域多场次洪水进行模拟，对模型模拟的洪水三要素与实测值进行误差对比分析，并绘制出部分场次洪水模拟过程图，结果表明，改进后的模型模拟效果较好。

（1）山区小流域的地下结构较为复杂，因此其产流规律也相对复杂，传统产流模型难以实现准确模拟。

（2）山区小流域的降雨具有很强的空间异质性，有限的雨量站测到的降雨可能无法反映真实降雨分布。

（3）应继续对改进模型加以完善，提高模型的模拟精度。

（4）伴随着全球气候变暖和水资源短缺的趋势，引来云端“活水”，高效利用空中云水资源将有助于改善生态环境。

（5）在未来的工作中，应尝试在长江流域及其他受山洪灾害影响地区选择有特点的典型小流域进行模型检验。同时，对地表气象学、植被和遥感数据进行广泛研究。建议在气候、土壤湿度和植物功能类型不同的地区，对基于壤中暴雨流机制及双源遥感地表蒸散量估算方法进行更深入的评估和验证。

参考文献：

[1] 何长高， 董增川， 陈卫宾. 流域水文模型研究综述[J]. 江西水利科技， 2008，34（1）：20-25.

[2] DUNNE T. Field studies of hillsope flow processes[J]. Hillslope Hydrology， 1978：227-293.

[3] KIRKBY M J， CARSON M J. Hillslope Form And Process[M]. Cambridge： University Press， 1972.

[4] DINGMAN S L. Physical hydrology[M]. Illinois：Waveland Press， 2015.

[5] 芮孝芳. 径流形成原理[M]. 南京. 河海大学出版社， 1991：156-197.

[6] 文佩. 基流分割及基于改进TOPMODEL径流模拟[D]. 南京：河海大学， 2006.

[7] MIRUS B B， LOAGUE K. How runoff begins （and ends）： Characterizing hydrologic response at the catchment scale[J]. Water Resources Research， 2013，49（5）：2987-3006.

[8] DICKSON B L. Recent advances in aerial gamma-ray surveying[J]. Journal of Environmental Radioactivity， 2004， 76（1）： 225-236.

[9] DOW C L， DEWALLE D R. Trends in evaporation and Bowen ratio on urbanizing watersheds in eastern United States[J]. Water Resources Research， 2000， 36（7）： 1835-1843.

[10] DUFFIE JONE A， BECKMAN WILLIAM A. Solar Engineering of Thermal Process[M]. New Jersey：John Wiley& Sons Inc， 1991.

[11] FENICIA F， PFISTER L， KAVETSKI D， et al. Microwave links for rainfall estimation in an urban environment：Insights from an experimental setup in Luxembourg-City[J]. Journal of Hydrology，2012，464：69-78.

（编辑：李 慧）

Application of subsurface storm flow coupled with surface evapotranspiration in mountain torrents model

WANG Lian1， WANG Li1， ZHANG Gelian1， KUANG Wei1，2， ZHANG Yanjun2

（1. Middle Changjiang River Bureau of Hydrology and Water Resources Survey，Bureau of Hydrology ， Changjiang Water Resources Commission， Wuhan 430012，China;   2.School of Water Resources and Hydropower Engineering，Wuhan University，Wuhan 430072，China）

Abstract： The research of runoff generation and confluence mechanism of small basins in mountain area is rare， and the accuracy of the current model is relatively low. The runoff generation and confluence mechanism of mountain torrent was analyzed， and it was preliminarily determined that the main runoff generation mode was subsurface storm flow. The simulation models of mountain torrent were compared and selected. According to the flood regulation and storage function of the runoff generation and confluence mechanism， it was proposed that the subsurface flow should be analyzed from the microscopic perspective， and further by making the Boussinesq hypothesis， the mountain torrent simulation model based on subsurface storm flow coupled with surface evapotranspiration was developed. The model was applied to the flood simulation of the Qingshui River in Yunnan Province and it showed that the result accuracy of the proposed model was improved significantly.

Key words： subsurface storm flow; remote sensing evapotranspiration; TOPMODEL model; DTVGM model