小波迟滞混沌神经元系统及其应用

邱泽国，甄鑫鑫，徐耀群,2

(1.哈尔滨商业大学 计算机与信息工程学院，哈尔滨 150028; 2.哈尔滨商业大学 系统工程研究所，哈尔滨 150028)

混沌神经网络是在Hopfield神经网络中引入混沌动力学，利用混沌系统全局遍历的特点，可以有效的避免在解决优化问题时，陷入局部极小值[1-4].另一方面，研究发现，将迟滞动力学引入Hopfield神经网络构建的迟滞神经网络，可以提高神经网络的优化性能[5-6].LIU等学者将具有迟滞特性的激励函数引入混沌神经网络，提出具有混沌和迟滞特性的单神经元模型，并利用该模型解决优化问题，结果表明，该模型可以同时利用混沌和迟滞动力学，防止收敛到局部极小值[7].本文在此基础上，将两个相互偏离的Sigmoid与Gauss组合作为新的激励函数，提出小波迟滞混沌神经元.分析了模型中参数变化时对混沌特性的影响.对模型产生的时间序列进行随机性的检验，将其应用至图像加密算法中，并对加密结果进行性能分析.

1 小波迟滞混沌神经元动力系统

1.1 小波迟滞混沌神经元模型

本文在此基础上，将两个相互偏离的Sigmoid与Gauss组合作为新的激励函数，提出小波迟滞混沌神经元，表示为：

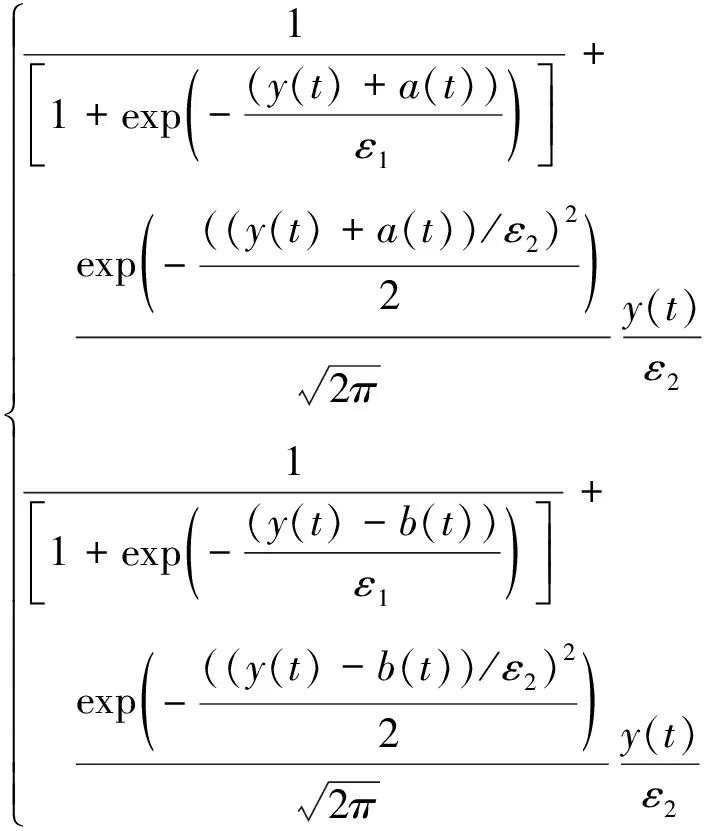
(1)

y(t+1)=ky(t)-z(t)x(t)+h

(2)

z(t+1)=(1-β)z(t)

(3)

a(t+1)=(1-β1)a(t)

(4)

b(t+1)=(1-β2)b(t)

(5)

其中：y(t)是神经元在t时刻的内部状态；x(t)为激励函数即神经元在时刻的输出；k表示神经元保留内部状态的能力，取值范围为0≤k≤1；β是退火速度参数.

Sigmoid与Gauss组合的函数是非单调的，但总体上呈递增趋势，可以有效地提高混沌搜索的效率.图1为本文所使用的迟滞激励函数图像.相比于单函数激励函数，迟滞激励函数的学习效率更高，并不容易到达饱和状态.当神经元在t时刻的输入大于(t-1)的输入时，则采用激励函数A；当当神经元在t时刻的输入小于(t-1)的输入时，则采用激励函数B[8-9].

图1 小波迟滞激励函数Figure 1 Wavelet hysteretic excitation function

1.2 小波迟滞混沌神经元的动力学行为

由神经元模型可以看出，I影响神经元的混沌动力学行为的有5个参数，将其余参数固定，通过改变其中一个参数来观察导致混沌的分支序列.将参数设置为r=250,z=-0.1,k=0.6,h=0.01.绘制分岔图以及Lyapunov指数图[10]分析小波迟滞混沌神经元模型的动力学行为.

图2、3是z变化时所对应的分岔图和Lyapunov指数图.由图可知，两者之间有明显的对应关系，混沌状态下的Lyapunov指数大于0.图2显示了多个进入和退出混沌的过程，在进化过程中，混沌不是连续的.

图4、5分别是参数k,r,h变化时所对应的分岔图和Lyapunov指数图.由图可知，参数k和r是在大范围内出现混沌现象，而参数h的混沌现象只有小范围，并且呈对称趋势.

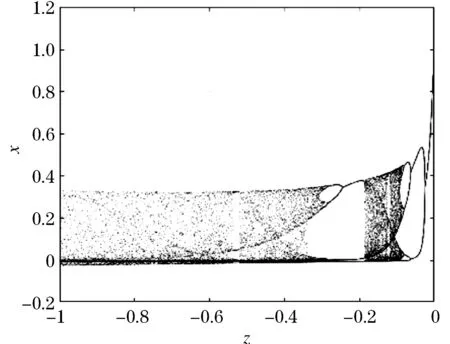
图2 参数z对应的分岔图Figure 2 Bifurcation diagram of parameter z

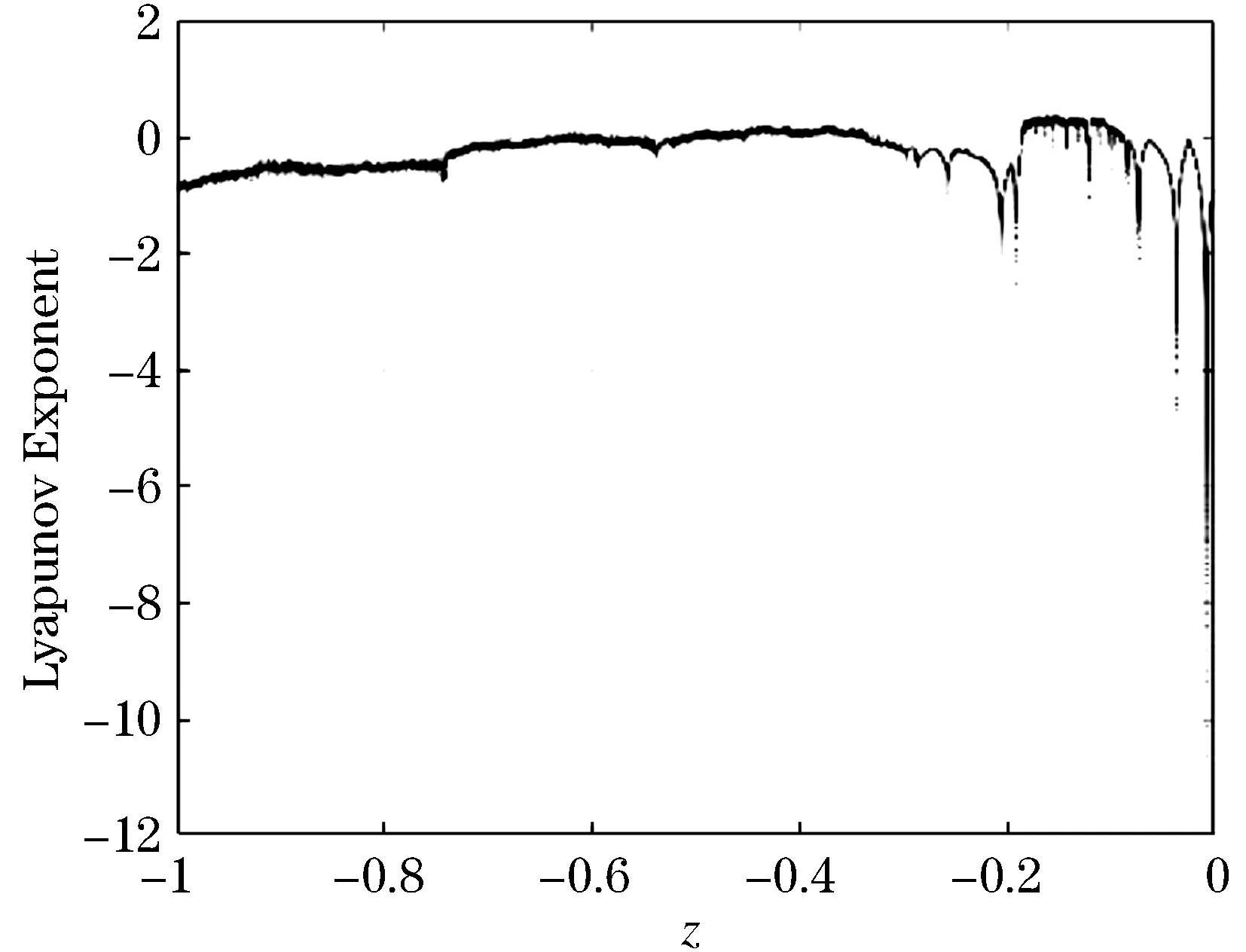
图3 参数z对应的Lyapunov指数图Figure 3 Lyapunov diagram of parameter z

图4 参数k.r,h变化时所对应的分岔图Figure 4 Bifurcation diagram of parameter k.r,h

图5 参数k.r,h变化时所对应的Lyapunov指数图Figure 5 Lyapunov diagram of parameter k.r,h

图6、7为参数a,b变化时所对应的分岔图和演化图，本文取a=b.根据神经元的混沌状态，合理选择参数，可以神经元同时具有迟滞性和混沌性，优化网络性能.

1.3 随机性检测

为了验证小波混沌神经元产生的随机序列的安全性，对随机序列进行公式的处理，将其转为二进制，利用NIST统计测试对序列进行随机性检验.

si=(1010×v′i)mod1

(6)

(7)

NIST测试需要进行15次随机测试，并在测试结束时输出P值.当P大于0.01时，表示数据集的随机性检测成功.

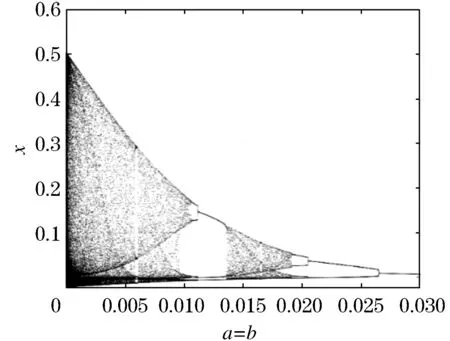
图6 参数a=b变化时所对应的分岔图Figure 6 Bifurcation diagram of parameter a=b

图7 参数a=b变化时所对应的Lyapunov指数图Figure 7 Lyapunov diagram of parameter a=b

本文测试了1 000 000位二进制数据，结果如表1所示.由表1可以看出，该序列通过NIST的随机数测试，可以应用于图像加密.

表1 随机序列的测试结果Table 1 Test result of random sequence

2 图像加密

2.1 彩色图像加密算法

彩色图像加密算法的具体步骤如下：

1)将大小为M×N×3的原始彩色图像按照R,G,B通道分为3份，其中:M、N分别为图像A的行列维数.

2)对图像R(i,j)加密，利用公式(1)，迭代M次和N次生成两个实数序列{xN}和{yM}.

3)利用公式对序列进行处理，将数值大小归一化至(0，255)，得到新的序列a和b.

a=floor(x(i)M)+1

(8)

b=floor(y(i)N)+1

(9)

4)对图像进行置乱操作，将图像的行列位置按照序列a和b组成的置乱矩阵进行置换，得到置乱图像.

5)改变置乱图像的像素值，进行扩散处理，利用神经元模型，迭代M×N次生成序列{xm×n} 和{ym×n}.

6)取置乱图像中的像素值，设该点的序号为n.若n是奇数，则由公式(10)对序列{xm×n}构造为加密密钥；若n是偶数，则由公式(11)对序列{ym×n}构造为加密密钥.

key(n)=mod(floor(x1(n)*1015),256)

(10)

key(n)=mod(floor(y1(n)*1015),256)

(11)

7)利用之前得到的置乱图像里的像素值与加密密钥值进行异或运算，得到加密后的像素值.将图像中的所有像素点均执行操作后，则得到加密图像R′(i,j).

8)对图像G(i,j),B(i,j)进行同样的操作，得到G′(i,j)和B′(i,j).

9)将加密图像R′(i,j),G′(i,j)和B′(i,j)组合到一起，得到原始彩色图像图8(D)的加密图像.

原图像，加密图像和解密图像如图8所示.可以看出加密后的图像无法获取任何信息，满足图像加密的需求.

2.2 统计性能分析

2.2.1 信息熵

信息熵可以分析图像的不确定性，理论值为8.信息熵的值越接近8，说明图像中的像素值属于均匀分布，可以很好的抵抗统计攻击[11]信息熵的数学公式为：

(12)

其中：n表示图像的灰度等级，p(xi)表示灰度值xi出现的概率。对加密后的图像计算信息熵，得到的结果如表2.从表中数据得出，加密后的图像可以很好的掩藏信息并抵抗统计分析.

图8 (A)(D)原始图像；(B)(E)加密图像；(C)(F)解密图像Figure 8 (A)(D) Plain images;(B)(E) Encrypted images;(C)(F) Decrypted images

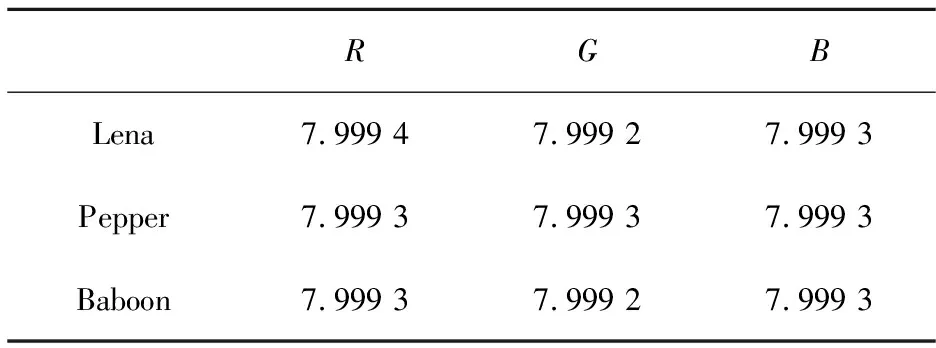
表2 信息熵Table 2 Information entropy

2.2.2 直方图分析

直方图分析图像中像素值的分布情况[12].图9中的(A)～(C)分别是Lena图像中RGB三个通道上的直方图，(D)～(F)则是加密图像中的直方图分布.两者相比，加密图像的直方图分布均匀，这意味着利用统计分析处理加密图像，从中获取的信息很少.

2.2.3 抗差分攻击

差分攻击是使用微小区别的密钥对加密图像进行攻击.一般使用像素数变化率(RNPC)和统一平均变化强度(IUAC)分析算法抵抗差分攻击的能力[13].

(13)

(14)

(15)

其中:M、N分别为图像的行列维数，C1、C2是由两张只有一个像素值不同的原始图像分别加密得到的加密图像.

图9 (A)(B)(C)原始图像的直方图； (D)(E)(F)加密图像的直方图Figure 9 (A)(B)(C)Histograms of Lena plaintext image; (D)(E)(F)Histograms of encrypted image

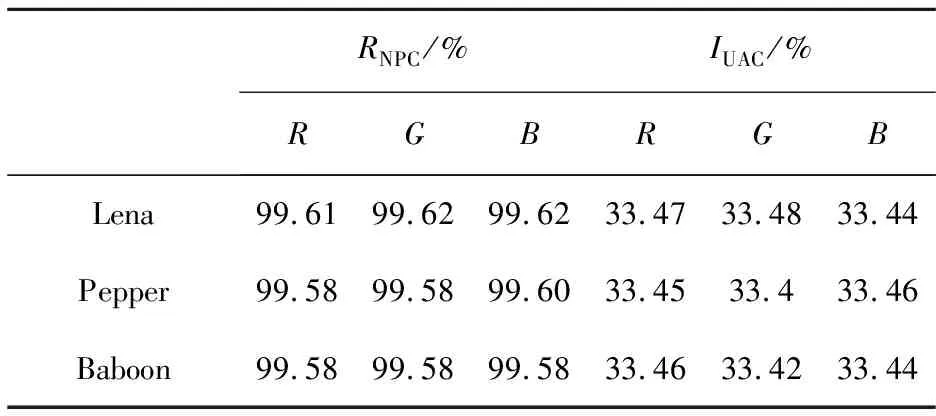
表3 RNPC和IUAC的结果Table 3 Result of RNPC and IUAC

RNPC和IUAC的理论值为99.609 4%和33.463 5%.从表3中的数据得出，两者的计算结果均接近理论值，该算法可以很好地抵抗差分攻击.

2.2.4 相关性分析

相邻像素值之间具有一定的相关性.也就是说，相关性越强，越容易从图像中获得信息[14].

图10展示了Lena的原始图像和加密图像在三个方向的相关性分布.很明显，加密后的图像在一定程度上削弱了相邻像素的相关性，可以很好的抵抗统计攻击.

图10 Lena的相关性分布 (A)(D)水平； (B)(E)垂直；(C)(F)对角；Figure 10 Correlation distribution in of Lena (A)(D) Horizontal; (B)(E) Vertical; (C)(F) Diagonal

2.2.5 噪声攻击

鲁棒性是算法受到攻击时保证稳定性的能力.在加密图像中添加噪声模拟受到的攻击，并利用其解密，观察解密图像.在加密图像中分别添加15%和25%的椒盐噪声[15]，得到的解密图像对应为图11、12.很明显，随着噪声添加的增多，得到的解密图像的清晰度降低，但仍能识别出原始图像中的有效信息，证明该算法可以很好地抵抗噪声攻击.

图11 添加15%噪声的解密图像Figure 11 The decrypted image added with 15% noise

图12 添加25%噪声的解密图像Figure 12 The decrypted image added with 25% noise

3 结 语

基于两个相互偏离的Sigmoid与Gauss组合作为新的激励函数，本文提出小波迟滞混沌神经元,分析了该模型在不同参数影响下的动力学行为，并选取合适的参数，分析生成的时间序列，验证其随机性，并应用于彩色图像加密算法中.