综采面支架工作阻力的PCA-SVR预测模型

吕文玉，丁 科，伍永平，杜旭峰，胡 馨，罗香玉，张 勇

(1.西安科技大学 能源学院，陕西 西安 710054；2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室，陕西 西安 710054；3.中国矿业大学(北京) 化学与环境工程学院，北京 100083；4.西安科技大学 计算机科学与技术学院，陕西 西安 710054；5.山西省潞安集团司马煤业公司，山西 长治 047105)

0 引 言

煤炭是中国的主要能源，对中国国民经济和社会发展具有重要的意义。近年来，随着开采深度和强度的不断增加，煤炭产量也在不断增加，各种矿井灾害更发生加频繁，其中顶板事故的发生占据较大比重，所以提前预测顶板压力，提前做好预防措施有利于矿井安全高效生产[1-4]。

在研究煤矿安全高效开采的过程中，非常重要的一项工作就是计算煤矿工作面液压支架的工作阻力。目前，综采面支架工作阻力主要采用力学理论分析，现场实测，数值模拟实验，工程类比等。刘国柱为验证8.8 m大采高液压支架的承载能力，依据神东矿区矿压显现规律和理论分析经验，建立了以采高和工作面长度为因变量的支护强度多元线性回归模型[5]。杨路林采用理论分析确定了顶板的直接顶，基本顶重力，上覆岩层静载荷是矿压的来源，采用位态方程和统计相结合的方法，确定了近距离煤层群顶板压力的理论值[6]。张仲伦基于大采高工作面矿压显现特点，从工作面直接顶关键层的结构出发，并通过理论分析，数值模拟验证的方法，建立了大采高综采工作面的支护强度计算公式[7]。由于矿压机理及控制具有高度的混动性，动态性与非线性特点[8]，在传统的计算方法中存在误差大、计算困难等问题[9]。

近年来，国内外许多学者将目光投向基于机器学习建立的预测模型，并取得了较好的预测效果。相比传统计算方法，机器学习具有快速、高效、可靠、实时等优良特点。以浅埋煤层开采部分数据为研究对象，借助主成分分析法，通过对变量的相关系数矩阵的内部结构计算分析，获取少数几个具有正交性且能代表原始变量的主成分，对数据进行简化，不仅最大程度地保留了原有信息的完整性，而且大幅度地减少了运算量，克服了多因素的相关性及反映信息在一定程度上存在重叠性等缺点[10]。后续使用的回归型支持向量机(SVR)在非线性回归方面取得良好的性能和效果[11]。SVR模型具有优秀的泛化能力且结构化风险较小，将主成分分析(PCA)降维后得到的主成分因子输入到该SVR模型，能够较好的处理复杂的非线性数据，并且迭代次数较少、快速收敛，该算法模型能够快速、准确预测支架工作阻力。

1 PCA-SVR算法

1.1 主成分分析

主成分分析(principal component analysis，PCA)最先是由皮尔逊和霍特林提出。主成分分析思想主要是用少数的若干新变量(原变量的线性组合)替代原变量，新变量要尽可能多地反映原变量的数据信息，新变量之间相互正交，可以消除原变量中相互重叠的信息[12-13]。数学模型如下。

对于一个样本，样本的标准化输入变量矩阵为

(1)

构造一个变量P1满足

P1=Xt1,‖t1‖=1

使得P1能携带Xnk的信息，即

(2)

1.2 支持向量机

支持向量机是一种新的机器学习方法。机器学习主要目的是基于样本数据建立数学模型来研究因变量(输出值)与一个或多个自变量(输入值)之间的关系，以便对未来做出预测或决策，而无需经过明确的编程。

20世纪90年代VLADIMIR和CORINNA最早提出现代版支持向量机，支持向量机最初研究线性可分的问题，将数据映射到一个新的高维表示，支持向量机在这个高维空间中找到一个具有最大边界的线性的超平面，尽量让超平面与每个类别最近的数据点之间的距离最大化，从而计算出良好决策边界，这样决策边界可以很好地推广到训练数据集之外的新样本数据集[14]。SVR为了解决拟合方面的问题，其基本思想是寻找一个最优分类面使得所有样本集离该最优分类面的误差最小。同时支持向量机模型适用于非线性的小样本学习，学习速率快且迭代次数较少的优点[15]。因此，SVR模型能够满足综采工作面支架工作阻力快速、准确预测的要求。SVR回归模型结构如图1所示。

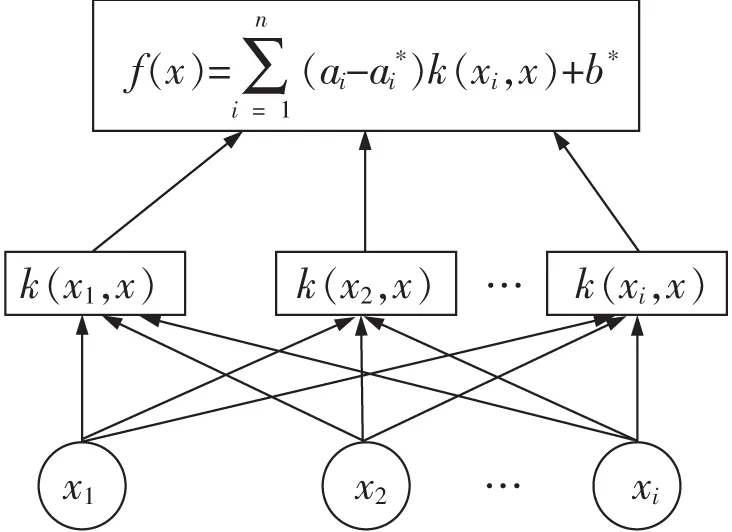
图1 SVR结构示意Fig.1 SVR structure sketch

在SVR算法中，核函数通过特征变换增加新的特征，使得低维空间中的线性不可分的问题变换为高维度空间中线性可分的问题，因此选择合适的核函数对于支持向量机的回归性能有很大的影响。在 SVR算法中，为了使预测结果具有更高的精确度[16]，在对样本进行训练之前，为了选择适合样本数据的核函数，随机挑选20组样本与10组测试集进行对比实验，具体结果见表1。

从表1可以看出，不同的核函数对于SVR算法的回归性能有很大的影响，高斯径向核函数无论均方误差(MSE)还是相关系数(R2)都较多项式函数、Sigmoid函数的拟合均具有明显优势，因此文中支持向量机算法模型选取泛化能力最好的核函数径向基核函数，通过交叉验证法寻找最优参数宽度以及惩罚因子c。径向基(RBF)函数的表达式为

(3)

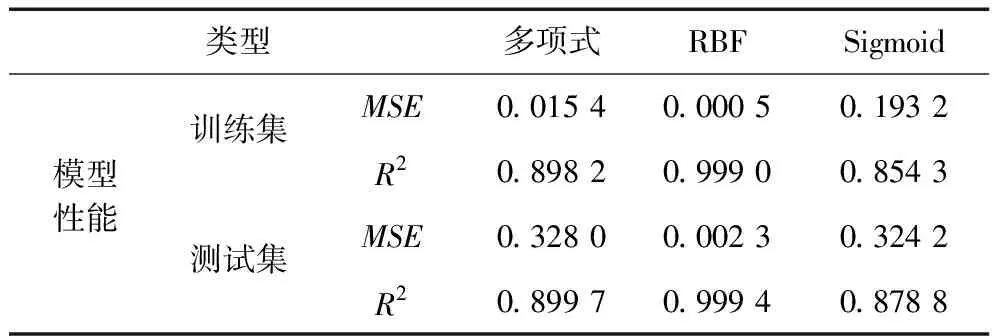
表1 不同核函数对模型性能的影响Table 1 Influence of different kernel functions on model performance

2 工作面支架工作阻力预测模型

目前，针对综采工作面支架工作阻力预测方法大致分为2类：一是基于传统弹性力学与岩石力学分析矿压顶板结构的力学方法；二是基于煤矿海量数据，利用人工智能方法挖掘数据间客观存在线性、非线性依赖关系，从而达到预测为目的智能技术方法[17]。文中是一种基于支持向量机与主成分分析(PCA-SVR)组合模型的机器学习算法对综采工作面支架工作阻力预测的方法。

2.1 数据预处理

综采工作面支架工作阻力的影响因素有很多，而影响支架工作阻力的波动方向和显著程度不尽相同。根据相关研究，选取了埋深、煤层倾角、工作面走向长度、工作面倾斜长度、直接顶厚度、基本顶厚、采高、煤厚、顶板条件8个参数作为为影响工作面支架工作阻力的输入特征，输出参数选择了工作阻力[18]。在数据收集过程中发现，煤层顶板条件是指工作面顶板的控制难易程度(岩性和节理为主要指标)，现为了方便机器学习，将其顶板条件按顶板控制程度分别用1，2，3，4代替不稳定顶板、中等稳定顶板、稳定顶板、非常稳定顶板。现采集到的79组浅埋煤层开采数据样本，69组数据用于训练模型，10组样本数据进行仿真预测。由于输入数据的每个特征(比如埋深、采高、工作面长度等)都有不同的取值范围，将取值范围差异很大，且单位不一样的数据输入到神经网络中，将导致神经网络收敛速度慢，训练时间较长，且如果网络自动适应这种取值范围不同的数据，数据范围较大的输入在模型拟合中对结果影响偏大，而数据输入范围小的输入作用偏小，机器学习肯定变得更加困难。对于这种数据，将对每个输入数据进行标准化处理。各个工作面的支架工作阻力及其主要影响因素数据见表2。

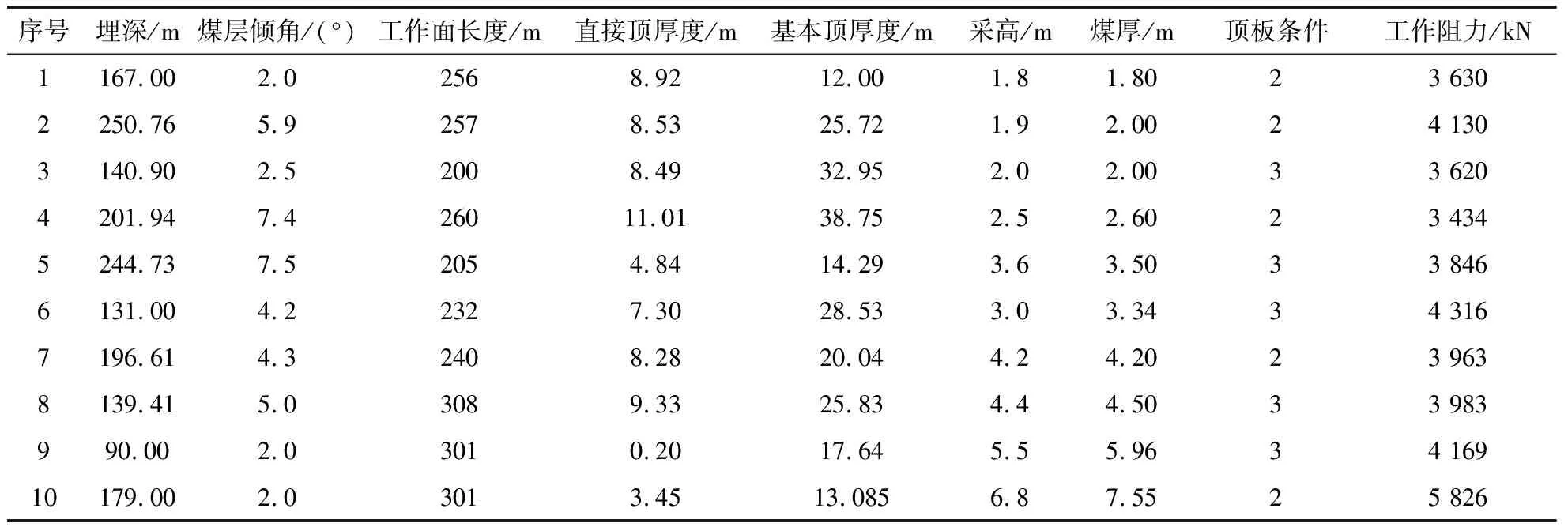
表2 工作面的支架工作阻力及其主要影响因素Table 2 Support working resistance of each working face and its main influencing factors

2.2 预测模型

利用MATLAB仿真软件，设计一种PCA-SVR算法，建立了一个综采工作面支架工作阻力的预测模型。根据VAPNIK等人的研究可知，支持向量机性能的主要影响因素为支持向量机的核函数、参数g以及惩罚因子c[19]。高斯径向基函数在之前样本数据预处理中表现出良好的性能，因此采用径向基函数作为SVR的核函数。

惩罚因子c起着控制错分样本惩罚程度的作用，从而实现错误划分样本的比例与算法复杂度间折中[20]。支持向量机模型的性能除了受核函数类型、惩罚因子c的影响还受到核函数参数g(核函数中的方差)的影响[21]。文中利用交叉验证方法寻求最佳核函数参数g和惩罚因子c的参数组合，同时，当模型性能相当时，优先选择惩罚因子c比较小的组合参数可以减少计算时间，建立训练模型。

综上，将标定好的数据集分成2部分，使用69组训练集样本进行训练，10组测试集进行仿真测试，根据核函数参数和数据样本分布之间的经验，并进行数次实验分析模型参数，对比模型性能，最终选取较佳惩罚因子c=20和核函数参数g=0.8。

3 实验结果分析

通过计算机仿真实验的SVR和 PCA-SVR模型分别对测试组工作面支架工作阻力进行预测，用MSE、R2作为评价指标，结果见表3。

从表3可以看出，PCA-SVR算法在利用主成分分析法对8个影响综采工作面支架工作阻力的因素进行降维分析4个综合因素后，各成分得分如图2所示。收敛速度0.97 s明显较SVR算法的1.79 s快；从超平面拟合效果来看PCA-SVR算法的相关系数99.62%明显优于SVR 71.8%；从预测的准确程度来看，PCA-SVR的均方误差0.014较SVR的0.447更接近于0，表明支持向量机在结合主成分析法后误差明显减少，达到预期实验效果。

表3 SVR与PCA-SVR算法结果比较Table 3 Comparison of SVR and PCA-SVR results

图2 主成分贡献率Fig.2 Contribution rate of principal component

从图3可以看出，SVR最大误差25.68%，最小误差1.3%，平均误差17.86%，模型整理波动幅值较大，预测结果不稳定，精度较低，存在较大的偶然性；PCA-SVR算法最大误差16%，最小误差1.3%，波动幅值仅为 4.5%。因此SVR无论在误差还是在精度上，都取得了更好的效果。说明PCA算法在降低数据集维度的同时保存了原始数据携带的信息，实验结果表明PCA-SVR算法较SVR模型有较好的泛化性，更好实现综采工作面支架工作阻力的预测。

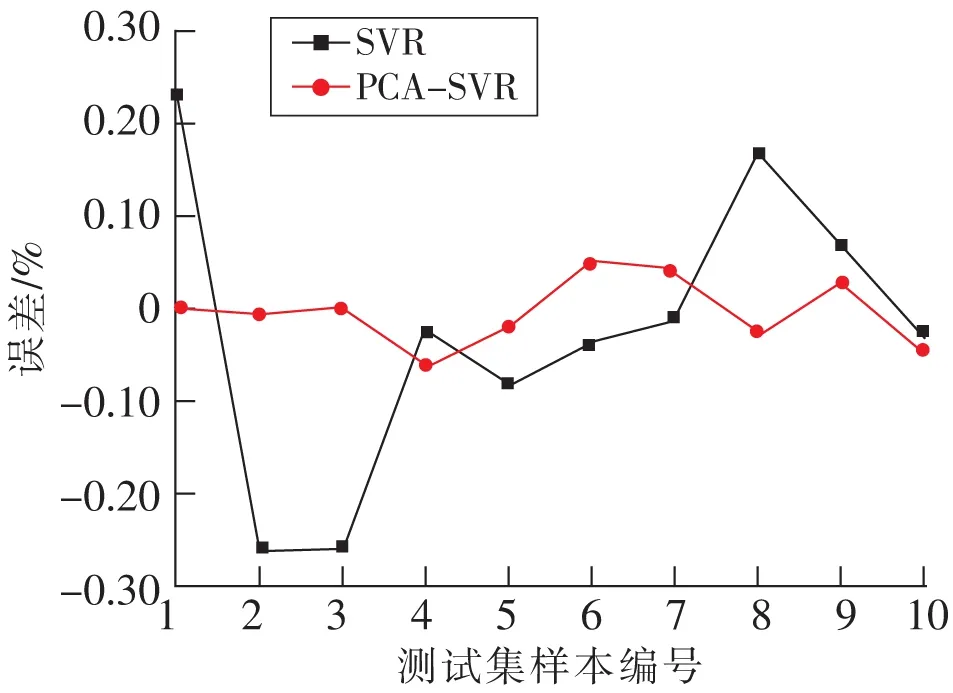
图3 SVR和 PCA-SVR模型误差Fig.3 Errors of SVR and PCA-SVR model

从图4可以看出，PCA-SVR模型的预测值与实际输出值拟合度明显高于SVR预测模型，但工作阻力7 000～1 200 kN拟合程度明显低于3 000～7 000 kN，这是由于样本数据在7 000～12 000 kN分布较少，支持向量机未能进行充分学习，但总体上PCA-SVR预测模型能够较好地预测综采工作面的支架工作阻力。

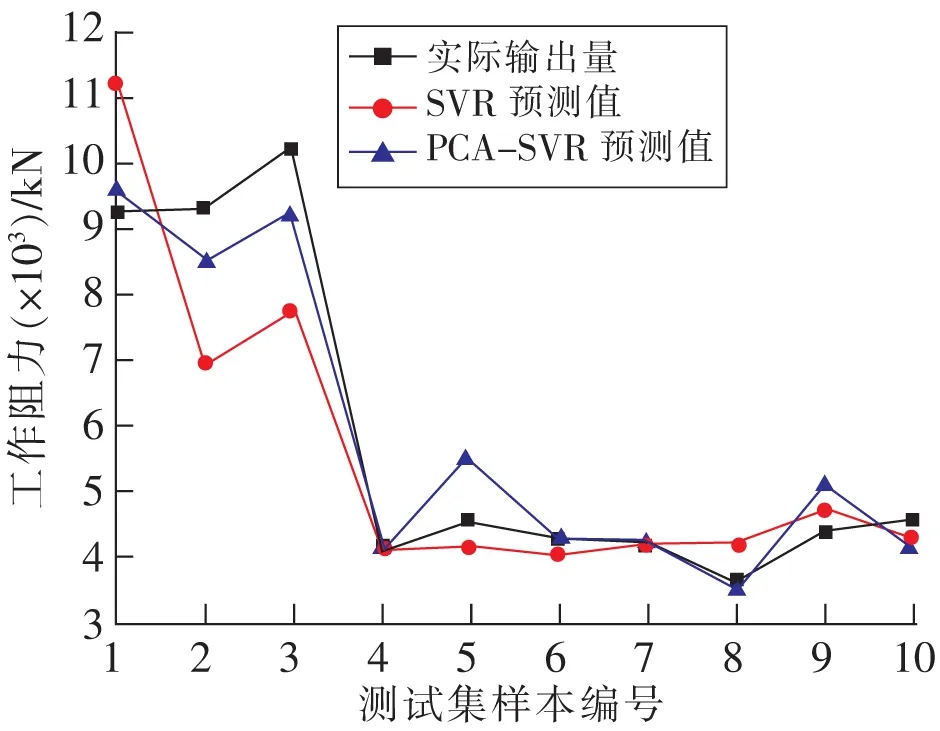
图4 PCA-SVR支架工作阻力预测效果Fig.4 PCA-SVR prediction effects of working resistance

4 结 论

1)综采工作面矿山压力是一个高度复杂的非线性机理，同时也受到了诸多因素的影响。利用 PCA-SVR神经网络模型来进行矿压规律的预测，较SVR模型缩短运行时间0.82 s，预测精度高99.6%。

2)用机器学习的方法预测综采工作面的支架工作阻力，与其他神经网络相比，支持向量机避免了陷入局部最小，且收敛速度较快。PCA-SVR预测模型性能优良，在浅埋煤层支架工作阻力预测中，泛化性较强。

3)PCA-SVR算法对综采工作面支架工作阻力的预测能够取得较好的效果，将该模型应用于综采工作面支架工作阻力的预测具有很强的现实意义和推广价值，但由于采矿地质环境复杂，采集数据困难，且存在较大误差，这给机器学习的算法编程带来较大的挑战，因此在建模前需要做大量精细化的数据收集工作，且PCA-SVR模型中的参数仍需进一步优化。