某大口径火炮身管坡膛结构优化设计
张鑫,于存贵,牛志鹏,梁林,邹利波
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国船舶重工集团公司第七一三研究所,河南 郑州 450015)
身管内膛烧蚀磨损主要集中在坡膛和膛线起始部[1],弹带挤进膛线时期,身管坡膛部分承受弹带巨大的挤压力与剪切力,弹带发生弹塑性变形,整个大变形过程持续到弹带挤进全深膛线后基本结束。挤进过程伴随着能量的转化与耗散,耗散的能量大多以热能的形式积聚在炮膛内,短时间内大量热量的积聚会加剧内膛的烧蚀磨损,对身管寿命不利。能量耗散规律与坡膛结构有很大关系,优化出合理的坡膛结构对提高身管寿命具有重要意义。
文献[2]通过试验与仿真结合的手段,对3种不同坡膛结构下的弹带挤进过程进行了有限元仿真,研究发现坡膛长度越长,挤进阻力越小;文献[3]运用显式非线性有限元算法对两种不同结构坡膛的挤进过程进行瞬态动力学数值模拟,研究发现短坡膛相比长坡膛工况,阳线起始点的法向接触力和剪切力峰值更大;文献[4]对不同坡膛锥度下内弹道性能的影响进行了对比分析。现有文献并未提出针对坡膛结构的优化方法。笔者从挤进过程能量转化与耗散角度出发,对某大口径火炮身管坡膛结构进行优化设计。
1 计算模型
1.1 仿真模型基本假设
仿真模型作出如下基本假设:忽略身管的后坐运动;忽略火药燃气的热因素对挤进过程的影响;弹体和身管在发射过程中只发生弹性变形;忽略嵌膛过程,即不考虑弹带的初始应力和变形;忽略身管和弹丸摩擦副的摩擦学状态改变,即采用恒定摩擦系数的“硬”接触。
1.2 有限元网格的划分
有限元模型的网格质量会影响计算结果,某大口径火炮身管坡膛锥度为1/10,身管有限元网格划分采用节点偏移方法[5],线膛身管有限元网格模型如图1所示,身管网格采用C3D8R单元,坡膛处网格大小为2 mm。弹丸为底凹弹,其有限元网格模型如图2所示。弹带结构如图3所示。


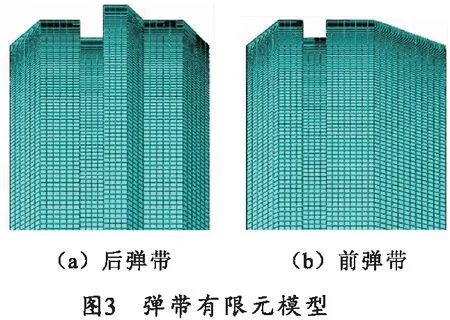
1.3 材料模型
身管材料为炮钢,弹体材料为弹钢,弹带材料为黄铜,材料参数如表1所示。

表1 材料参数
弹带挤进过程涉及高应变率下材料的塑性变形及断裂失效问题,传统的静态或准静态材料应力应变关系已不能描述挤进过程。笔者采用可描述金属材料承受大变形、高应变率和高温下力学行为的Johnson-Cook本构模型[6]。
Johnson-Cook 塑性变形本构模型为
(1)

(2)
式中:T为材料实际温度;Tm为室温;T0为材料熔化温度。
Johnson-Cook断裂失效本构模型方程为
(3)
式中:D1、D2、D3、D4和D5为材料断裂失效本构常数;σ*为应力三轴度。
本构模型参数如表2所示。

表2 铜的Johnson-Cook本构模型参数
1.4 载荷及边界条件
弹底施加由内弹道方程解算出的压力曲线,如图4所示。边界条件为身管尾部全约束。
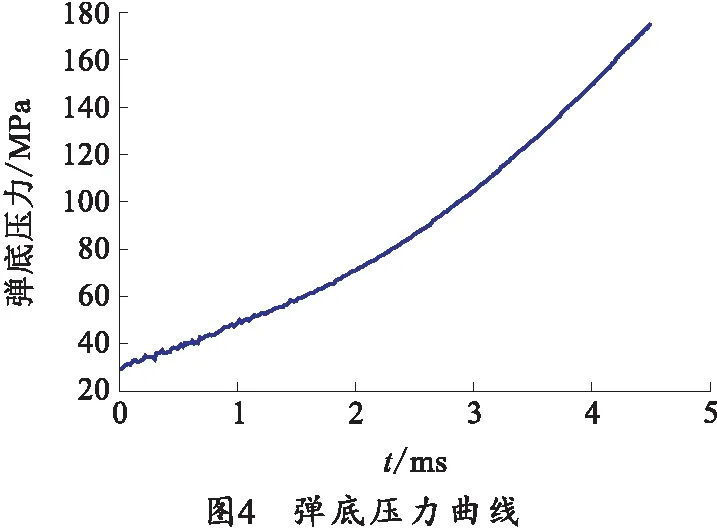
弹带、前定心部与身管内膛之间的接触算法设置为罚函数法,选择库伦摩擦模型,接触面之间的摩擦系数取0.1,建立的弹炮耦合有限元模型如图5所示。

2 挤进过程载荷及能量分析
2.1 挤进过程弹带受力分析
以弹带为研究对象,如图6所示,挤进过程弹带主要承受身管的作用力有法向接触力Fn和切向摩擦力Ff。

法向接触力为接触面正应力与接触面积的乘积:
(4)
考虑膛线缠角情况下,弹带所受力在炮膛轴线方向上的合力为
(5)
式中:φ为坡膛角,即坡膛母线与炮膛轴线的夹角;μ是摩擦系数;α为膛线缠角。
大口径榴弹炮弹带挤进膛线过程涉及几何、材料、边界非线性等问题,目前无法通过常规理论计算准确描述。有限元软件ABAQUS/Explicit能较好地模拟挤进过程的非线性力学行为[7]。挤进过程不同时刻弹带应力云图如图7所示。从图中可以看出,后弹带首先与坡膛内壁发生接触,随着挤进的进行,前弹带也与身管内壁发生接触,约2ms时刻,前弹带挤压膛线起始部,此时前弹带单位时间变形量达到峰值,因此接触力出现了一个极值;随着挤进的深入,弹带变形量逐渐增大,由于后弹带较前弹带挤入强制量大,塑性变形亦较大,因此后弹带与坡膛作用产生的作用力要大于前弹带产生的作用力,约2.75 ms时,前弹带刻槽基本完成,此时后弹带凸缘被压平,开始挤压膛线起始部,此时后弹带单位时间塑性变形量达到最大,接触力出现峰值;约3.9 ms时,弹带完全挤进全深膛线,弹带刻槽完成。

2.2 挤进过程能量损耗分析
挤进过程弹底压力做功除提供弹丸沿身管轴线运动以及绕自身轴线旋转运动以外,主要耗散在弹丸与内膛接触表面之间的摩擦能和弹带弹塑性变形能上,且摩擦耗散能与塑性变形能最终主要以热能的形式散失掉[8-9],还有一部分能量耗散在弹带材料损伤断裂失效等方面。忽略身管后坐能量与弹前空气阻力,根据能量守恒定律,弹丸挤进过程能量存在如下关系:
Ew=Ek+Ef+Ep+E′,
(6)
式中:Ew为弹底压力做功;Ek为弹丸动能;Ef为摩擦耗散功;Ep为弹带塑性变形能;E′为其他形式的耗散能。
挤进过程每一时刻有功率关系:
Pw=Pk+Pf+Pp+P′,
(7)
式中:Pw为某一时刻弹底压力做功的功率;Pk为单位时间内弹丸动能的增量;Pf为摩擦耗散功率;Pp为弹带塑性变形功率;P′为其他形式的耗散功率。
弹带与身管之间摩擦耗散功率可以写为
(8)
式中:f为弹带承受身管的切向摩擦力;v为接触面弹带上的节点在炮膛表面的滑移速率;m为在每一时间增量步中,弹带与身管接触的节点数量;n为挤进过程总共的增量步。
采用Fortran语言与有限元Explicit模块结合的方法[10],仿真计算出挤进过程各能量数据,其中摩擦耗散能与摩擦耗散功率通过子程序计算得出,塑性变形能、塑性变形功率和弹丸动能数据通过软件后处理模块提取得出。
某大口径火炮身管弹带挤进膛线过程各能量随时间的累积曲线如图8所示。
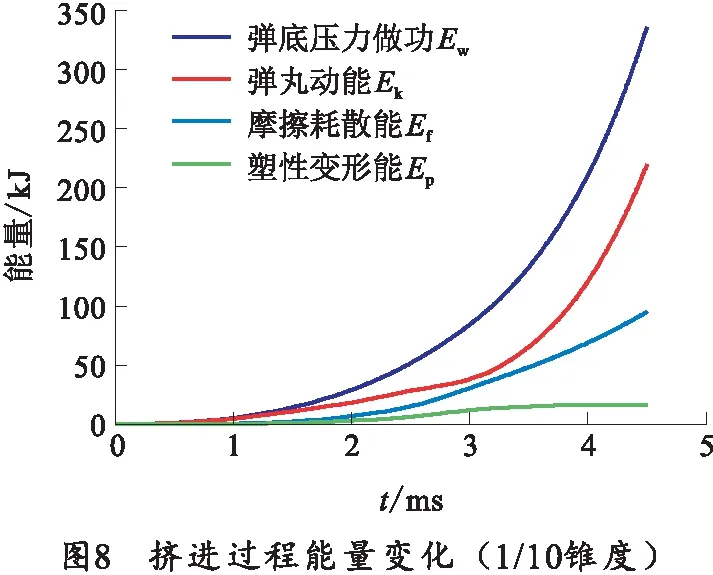
挤进结束后能量转化耗散占比情况如图9所示。
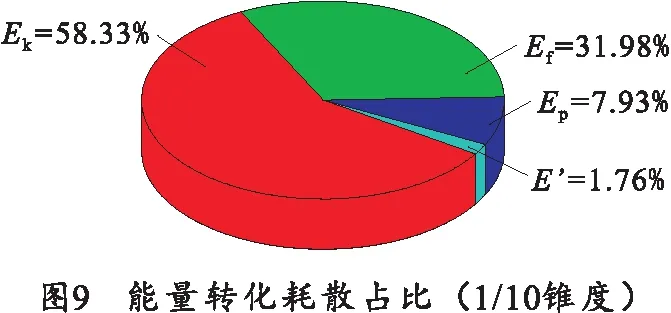
由图9可知,弹底压力做功主要转化为弹丸沿炮膛直线运动的动能,约占总能量的58.33%;其次是摩擦耗散能,约占总能量的31.98%;占比较小的是弹带塑性变形能,约占总能量的7.93%;其他耗散能占比最小,约为1.76%,本文予以忽略。
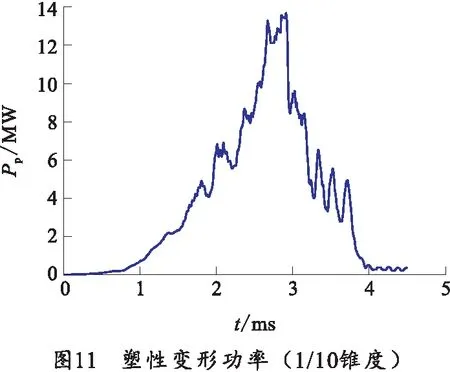
图10为挤进过程摩擦耗散功率曲线,由图可知,随着挤进的深入,摩擦耗散功率先增大后减小到0,在3 ms左右出现极值,此时单位时间内摩擦耗散能最大。图11为弹带塑性变形功率曲线,变化规律与摩擦耗散类似,当弹带逐渐完成刻槽后,塑性变形功率也逐渐减小,完全挤进膛线后,刻槽完成,弹带大变形结束,塑性变形功率趋于0。

3 身管坡膛结构优化
3.1 优化变量的选择及优化目标的确定
某大口径火炮身管内膛结构如图12所示,坡膛锥度K计算公式为
(9)
式中:d0为药室直径;d为阳线直径;l为坡膛长度。
在药室直径d0和阳线直径d一定时,锥度K由坡膛长度l决定。身管坡膛锥度的取值范围为1/60~1/5,常用锥度为1/10~1/5[11],笔者通过改变坡膛长度l建立不同锥度坡膛的弹炮耦合模型。

基于Archard磨损理论[12],滑动摩擦过程中单位磨损量可以表示为
(10)
式中:dM为单位磨损量;kv为体积磨损系数;Fn为正压力;v为滑动速度;H为表面硬度。
基于原子摩擦理论[13],可得到单位磨损量dM与摩擦功率(Fnv)成正比关系,即摩擦耗散功率越大,单位磨损量越大,且单位磨损量最大值出现时刻与接触力最大时刻重叠。摩擦磨损的积累会导致弹带挤进过程中弹丸的稳定性下降,弹带刻槽质量下降,从而影响弹带挤进过程的正常进行以及影响弹丸的运动状况[14],火炮连发射击时,高温火药燃气对内膛的交变作用使得身管不能完全冷却,相应的温度分布会作为下一发的初始环境温度,多发射击后,炮膛内的温度甚至接近炮钢的熔点温度[15],在这种临界状态下,微小的温度变化就会导致身管内膛部分位置的材料物相状态发生改变。由机械摩擦和塑性变形产生的耗散能大多以热能散失,且单位时间产生的热量越多,积聚在内膛中的温度越不容易在短时间内耗散,连续射击时,坡膛处受到弹带摩擦和弹带自身变形产生的交变热应力作用,导致内膛更易产生疲劳破坏。因此降低最大摩擦耗散功率与最大塑性变形功率有利于提高身管寿命。
综合以上分析,选择坡膛锥度K为优化变量,挤进过程摩擦耗散功率最大值PMf和塑性变形功率最大值PMp为优化目标。根据某大口径火炮身管坡膛实际结构,结合坡膛锥度的一般取值,确定某大口径火炮身管坡膛锥度的取值范围为1/16~1/5。
建立7种不同坡膛锥度的挤进模型并进行仿真,提取挤进过程各能量组成如表3所示。由表可知,随着锥度增大,挤进长度变短,弹底压力做功减小,弹丸获得的动能减小,摩擦耗散能减小,但不同坡膛锥度所消耗的塑性变形能基本相同,这是因为不考虑嵌膛作用的前提,不同工况下弹带的初始状态相同,挤进全深膛线后弹带刻槽情况基本一致,因此挤进结束后弹带总变形量相同,塑性变形能也就相同。

表3 不同锥度挤进过程各能量组成
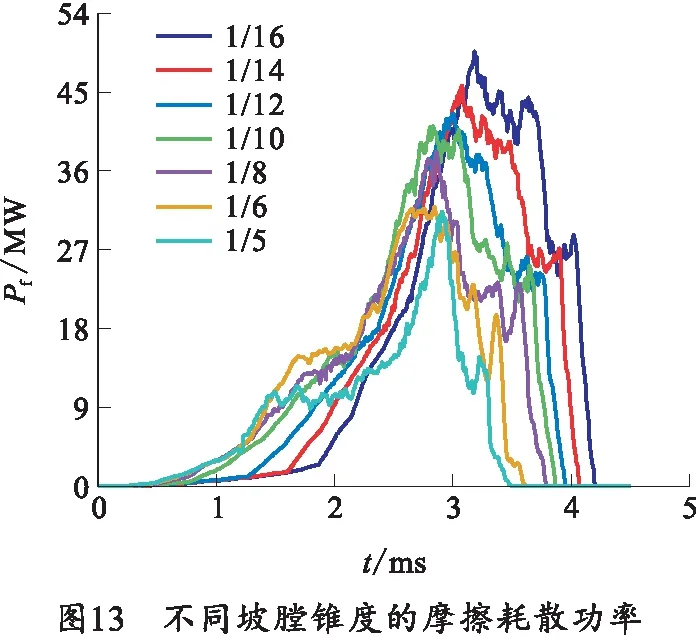
在弹带结构、装药量等一定的情况下,坡膛锥度直接影响挤进过程的坡膛阻力、接触面积以及弹丸运动速度,这会使得单位时间内弹带材料塑性变形量不同,因此导致塑性变形功率不同。摩擦耗散功率曲线如图13所示,塑性变形功率如图14所示。

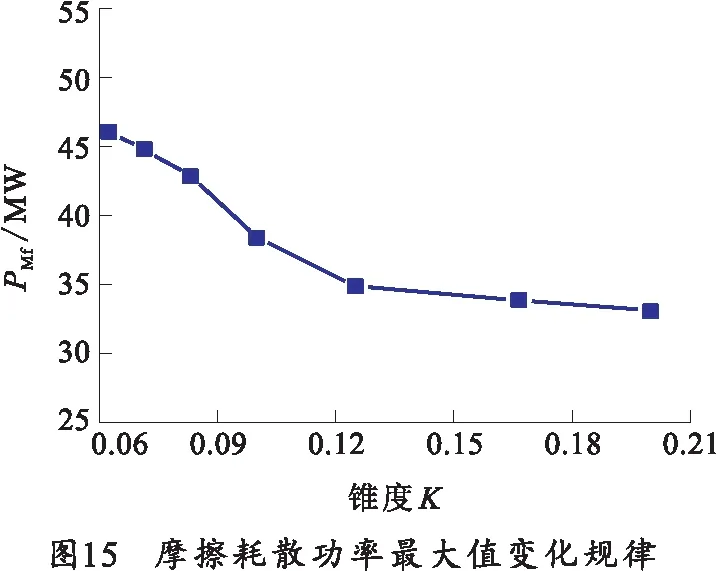
摩擦耗散功率最大值和塑性变形功率最大值随锥度变化的规律如图15、16所示。由图15和16可知,摩擦耗散功率最大值随坡膛锥度逐渐减小,在后期变化较为平缓。塑性变形功率随着坡膛锥度先减小后增大,在1/10锥度附近出现极小值,这是因为小锥度坡膛,弹带挤进初期所承受的法向接触力较小,弹带初期变形量较小,变形速率较平缓,但随着挤进的进行,弹带滑移速度加快,接触面积增大,尚未变形的材料较多,导致挤进后期弹带变形速率加快,塑性耗散功率最大值较大。随着锥度的增大,挤进初期接触力增大,起始变形量增大,挤进后期弹带未变形量减小,塑性变形功率最大值减小。当锥度大于1/10时,挤进初期弹带承受较大的阻力,单位时间变形量增大,塑性变形功率增大,随着锥度的增大,挤进距离更短,弹带挤进迅速,因此塑性变形功率最大值增大。

3.2 优化数学模型
坡膛优化为单因素多目标优化问题,采用线性加权法,将多目标转化为单目标优化,首先进行归一化处理,然后建立坡膛多目标优化评价函数:
(11)
式中:
(12)
式中:PMf为摩擦耗散功率最大值;PMp为塑性变形功率最大值;PMf0为初始坡膛锥度下摩擦耗散功率最大值;PMp0为初始坡膛锥度下塑性变形功率最大值;α和β为各优化目标的权重系数,满足α+β=1。考虑到摩擦损耗和塑性耗散对挤进过程的影响,选取α= 0.5,β=0.5,使两者处于同等重要的地位。
3.3 优化结果分析对比
对评价函数进行多项式拟合后,采用多岛遗传算法对目标进行寻优,设置种群规模为10,岛的个数为10,遗传迭代代数为50,变异概率和迁移概率为0.01,优化迭代过程如图17所示,最优解为0.119,取整后确定最优坡膛锥度K=1/9。

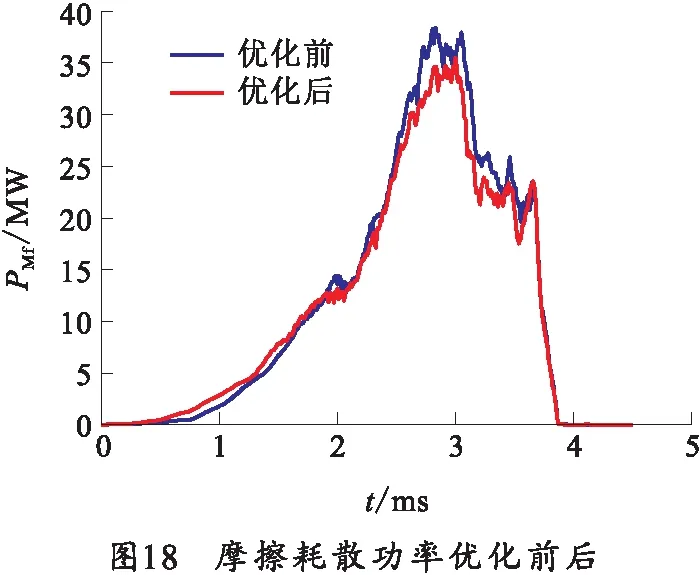
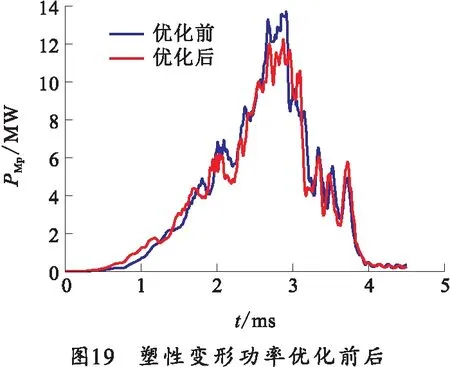
以优化参数建立弹炮耦合有限元模型,仿真结果如表4所示,优化后的摩擦耗散功率最大值减小了6.1%,塑性耗散功率最大值减小了19.0%,坡膛评价指标减小12.5%,优化前后摩擦耗散功率和塑性变形功率曲线对比如图18和19所示。
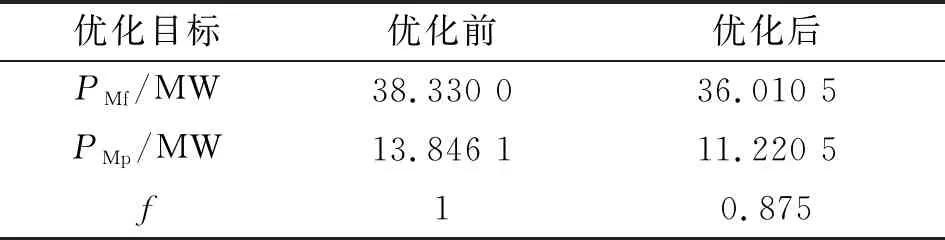
表4 坡膛优化前后对比
4 结束语
通过有限元方法建立某大口径火炮身管弹炮耦合有限元模型,仿真分析了挤进过程能量的转化与耗散规律,研究发现挤进过程有接近一半的能量通过摩擦做功和塑性变形损失掉,其中以摩擦做功耗散的能量最多。摩擦耗散功率最大值随坡膛锥度增大而减小,塑性耗散功率最大值与坡膛锥度之间存在非线性规律,即存在最优坡膛锥度。笔者以耗散功率最大值为优化目标,通过线性加权法建立坡膛优化评价函数,采用多岛遗传算法对坡膛结构进行优化设计。该优化方法可为火炮身管内膛结构设计提供一定的参考。

