点到直线的距离

吴华容

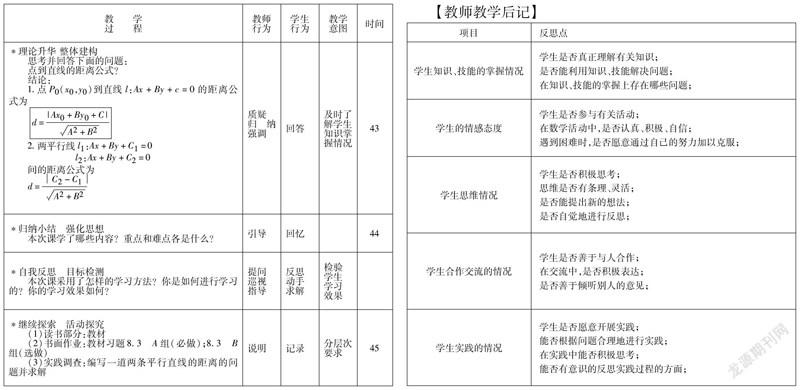
中圖分类号：A 文献标识码：A 文章编号：（2021）-44-489

【教学目标】

知识与技能：

（1）掌握点到直线的距离公式和两平行线间的距离公式;

（2）能应用点到直线的距离公式解题.

过程与方法：

培养学生的数学思维及分析问题和解决问题的能力.

情感态度与价值观：

1.体验数学活动中的受挫感和成功感，在质疑、交流中培养学生的合作意识和创新精神;

2.感受数学的应用价值，激发“学数学用数学”的热情。

【教学重点】

点到直线的距离公式与两平行线间的距离公式。

【教学难点】

点到直线的距离公式的应用。

【学情分析】

1.知识与能力：学生已经学习了两点之间的距离公式且具备直线的有关知识，学生对坐标法解决几何问题有初步的认识。

2.学生实际情况：中职学生自制力差，纪律松散，学习目标模糊，厌学严重。

【教学设计】

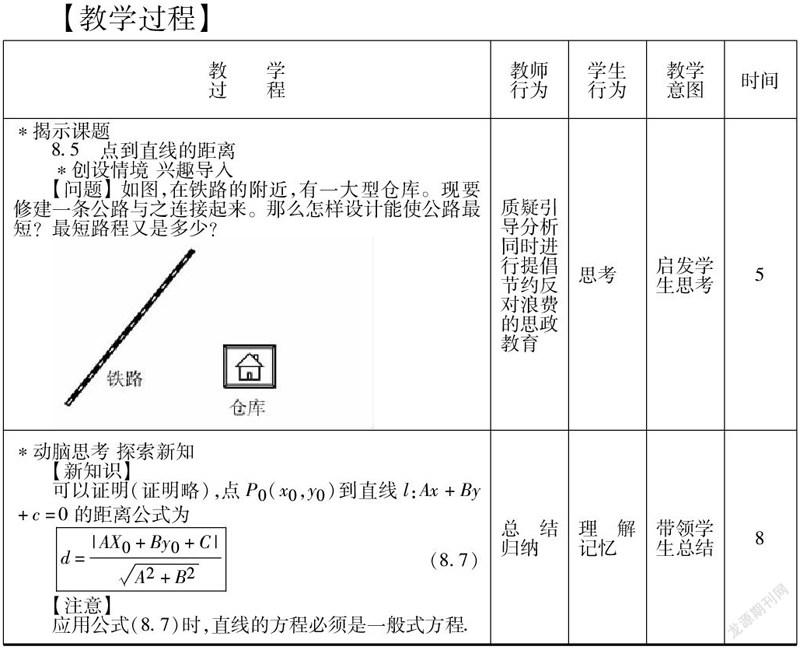
教材采用“数形结合”、“看图说话”的方法，导入点到直线距离公式，过程简单易懂.公式的推导过程过于繁琐，不要求学生掌握.运用公式时，要注意先把直线方程转化成一般式。例1是巩固性题目.属于基础性题.首先将直线的方程化为一般式方程，再根据点到直线的距离公式求解即可。例2是利用点到直线的距离公式推导出两平行线间的距离公式.这一系列解题程序，蕴含着“解析法”的思想方法.

需要强调，点到直线的距离公式中的直线方程必须是一般式方程.

【教学备品】

教学课件.

【课时安排】

1课时.（45分钟）

【教学过程】

像这样的例子还有很多，俯拾皆是，在此笔者就不一一举例了.上述都是通过给出具体函数，让解题者去猜想并证明恒等关系.也有些题目直接给出恒等式，在此也不再举例了.

三、结束语：

正如文[1]所说：“高考数学命题是一项创造性工作，把高考数学题进行开放性地创造引伸，推广也是开创性的工作.笔者认为：“作为一名数学教师不能仅仅局限于高考题本身，而应当理解命题的意图，为什么这样出题，巧妙之处在那里，能否进行推广、再创造.课本是创造的源泉、创造的依据，对课本习题进行再创造，不仅可以使学生从题海中解放出来，注重探索通解、通法，而且能够提升学生的思维能力，培养其创新精神和创新能力.在变化的过程中使学生感受数学美，享受学习的乐趣.

参考文献

[1].孟华 从一道高考试题的开放性教学看数学美 数学通报 2005 4