基于MATLAB_GUI的矩阵相关运算验证系统设计
聂奥洋 李军成







摘要:矩阵的相关运算是代数学中重要的内容,在许多领域也有着广泛的应用。为了对矩阵相关运算的结果进行验证,基于MATLAB的图形用户界面(GUI)平台设计了一个矩阵相关运算的验证系统。该系统通过调用MATLAB自带的有关函数进行设计,主要包括矩阵的运算、矩阵的求值、线性方程组求解等3个模块。用户只需根据提示信息输入相应的变量,系统即可快速给出矩阵相关运算的结果,为矩阵相关运算的验证提供了一个有效的平台。
关键词:MATLAB;图形用户界面;矩阵运算;验证系统
中图分类号:TP311 文献标识码:A
文章编号:1009-3044(2021)30-0088-04
1 引言
MATLAB将数值分析、矩阵计算、科学数据可视化等强大功能聚集在一起,为工程设计、科学研究等涉及数值计算的领域提供了灵活便捷的解决方案。MATLAB在矩阵运算以及线性方程组的求解中,拥有强大的计算功能,学生可以利用MATLAB高效地进行基本的矩阵运算[1]。
关于矩阵计算的GUI设计[2-4]有很多,但这些设计主要存在的问题有:1)界面不能用于矩阵的不同计算;2)界面设计过于复杂,不便使用。矩阵的理论和方法在数学和其他学科中都具有重要的意义,但许多学生无法克服矩阵庞大的计算量带来的恐惧,从而丧失了学习的兴趣和动力[5]。为此,本文对矩阵相关运算进行细化分类,通过MATLAB自带的函数设计了一个矩阵相关运算验证系统,为辅助教师的教学和学生的学习提供了便利。
2 系统的设计
2.1 系统主界面的设计
演示平台总界面的设计思路是将矩阵的所有相关知识点分成了以下三类:矩阵的运算、矩阵的求值、线性方程组求解,系统主界面的设计如图1所示。
2.2 矩阵的运算界面设计
2.2.1 矩阵的加法界面设计
矩阵的加法模块的界面设计如图2所示。该界面给出了和与差的定义以及运算规则,包含两个可编辑文本框,分别用来读取用户所输入的矩阵,然后通过按钮(计算A+B)和按钮(计算A-B)得出用户所需数值结果,结果会在按钮下方的列表框中显示。
2.2.2 矩阵的数乘界面设计
矩阵的数乘模块界面设计如图3所示。该界面给出了一些矩阵与数相乘的运算规律以及遵循的运算法则,让用户在使用该界面时同时可以增加用户对矩阵数乘知识的学习。该界面提供两个可编辑文本框,一个用来获取用户所输入的数k,另一个用来获取用户所需要计算的矩阵。
2.2.3 矩阵乘法的界面设计
矩阵乘法模块的界面设计与图4所示。跟矩阵的数乘运算类似,该界面设置两个可编辑文本框用于获取用户所输入的矩阵,列表框用于反馈结果。用户在可编辑框输入需要计算的矩阵,点击计算按钮,界面系统会自动通过MATLAB所包含的函数对输入矩阵进行处理反馈结果。
2.2.4 矩阵求逆的界面设计
矩阵求逆模块的界面设计如图5所示。该界面给出了矩阵求逆的一些相关理论知识和编辑文本框、按钮等操作按键。用户通过对可编辑框的编辑,使MATLAB利用get函数获取到所需要加工的矩阵,然后利用程序所指定的符号对矩陣进行求逆,最后通过列表框反馈。
2.2.5 矩阵转置的界面设计
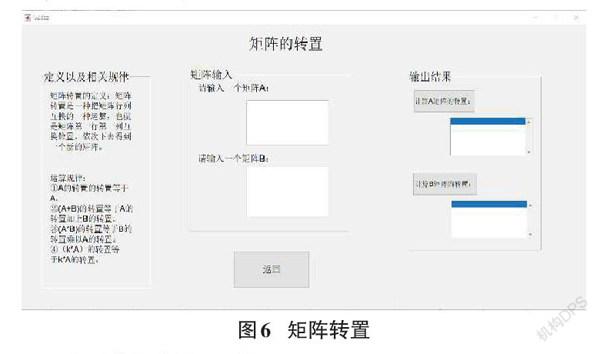
矩阵转置模块的界面设计如图6所示。该界面利用MATLAB转置运算符对用户输入的矩阵进行加工,得出矩阵的转置。在该界面的左边主要给出的是矩阵转置的相关知识点和转置运算的规律,方便用户学习,中间部分设置两个可编辑文本框提供给用户输入他们想处理的矩阵,模块右边是矩阵处理的按钮以及处理过后结果的显示。
2.2.6 矩阵共轭的界面设计
矩阵共轭模块的界面设计如图7所示。该界面相比于矩阵转置模块的设计区别在于矩阵共轭转置研究的是复数矩阵。
2.3 矩阵的求值界面设计
2.3.1 矩阵行列式计算的界面设计
行列式是方阵的一个非常重要的指标,其计算本身具有一定的复杂度[6]。矩阵行列式计算的界面设计如图8所示。该界面左边排版方阵行列式的运算性质,中间利用get函数设计交互框用于提取用户所输入的矩阵,右边利用MATLAB中det函数对get到的矩阵进行处理反馈数据,注意所输入的矩阵必须为方阵不然会提示错误。
2.3.2 矩阵求秩的界面设计
矩阵的秩应用性十分广泛,尤其是在判定向量组的线性相关性、求解方程组的解的结构以及判定矩阵行(列)空间的基和维数上的应用更为常见[7]。矩阵求秩的界面设计如图9所示,该界面主要利用MATLAB rank函数精确快速地得出矩阵的秩。
2.3.3 矩阵求迹的界面设计
矩阵的迹作为矩阵的一个重要数字特征,在数值计算、逼近论和统计估计等方面都有着较为广泛的应用[8]。矩阵求迹的界面设计如图10所示,该界面的设计类似于矩阵行列式的模块进行设计,在界面给出有关矩阵求迹的相关知识点,利用MATLAB已知函数trace函数,对矩阵进行加工并反馈结果。
2.3.4 矩阵特征值与特征向量计算的界面设计
特征值与特征向量的理论体系已经基本成熟,并且在其他领域中得到了广泛的应用[9]。矩阵特征值与特征向量计算的界面设计如图11所示,该界面给出了特征值和特征向量的相关知识点,主要通过eig函数帮助用户快速计算矩阵的特征值与特征向量。
2.3.5矩阵计算范数的界面设计
矩阵计算范数的界面设计如图12所示,该界面给出了范数的定义,用get函数设计了可编辑框用于读取用户输入的矩阵,再针对输入矩阵计算不同的范数结果。
2.3.6 矩阵条件数计算的界面设计
矩阵条件数计算的界面设计如图13所示,该界面的设计与矩阵范数模块的设计类似,给出了条件数的定义,用get函数设计了可编辑框用于读取用户输入的矩阵,再针对输入矩阵计算不同的条件数结果。
2.4 线性方程组求解的界面设计
求解线性方程组是代数学中重要的知识模块,在网络流模型,动物迁徙模型[10]求解中也具有广泛应用。线性方程组求解的界面设计如图14所示,该界面主要是利用矩阵的性质进行线性方程组有无解的判定和求解,对于有解的线性方程组可以利用常数矩阵和系数矩阵求解出该方程的解。用户首先输入线性方程组的系数矩阵、增广矩阵、未知数个数以及等式右边的常数向量,然后点击判定方程组是否有解,如果此方程组有解则可点击求解得到此方程组的解。
3 结束语
本文将矩阵相关运算具体分为矩阵的运算、矩阵的求值、线性方程组求解等3个模块,基于MATLAB_GUI设计与开发了一个矩阵相关运算的验证系统。所设计的系统界面美观,功能齐全,运行稳定。在进行操作时,只需修改可编辑框参数,便可得到所需要的数据,通过该系统可以解决一些较复杂矩阵的计算。
参考文献:
[1] 寇娜.MATLAB在线性代数理论教学中应用的探索[J].教育教学论坛,2020(29):306-307.
[2] 郝琳,马长林.Matlab/GUI的AHP成对比较矩阵的检验及修正[J].电脑开发与应用,2014,27(9):76-78.
[3] 杨凤英, 廖莎. 基于Matlab GUI线性代数计算器的设计与开发[J]. 甘肃科技, 2019, 35(21): 1-3.
[4] 崔秋珍.基于MATLAB的《线性代数实验课程》GUI平台设计与实现[J].电脑知识与技术,2012,8(31):7513-7515,7522.
[5] 杨亚辉.用Matlab深入学习和理解矩阵知识[J].现代电子技术,2007,30(6):175-177.
[6] 胡康秀,杨扬,丁云,等.3类典型的“矩阵和”的行列式计算及其应用[J].江西科学,2020,38(5):619-620.
[7] 谢毅,徐聪.矩阵的秩的三种常见的应用[J].数学学习与研究,2020(9):154,156.
[8] 宿曈.矩阵迹的性质及其应用[J].高师理科学刊,2018,38(10):45-47.
[9] 张亚. 矩阵的特征值与特征向量及其应用[J]. 科技经济导刊, 2018, 26(11): 79-84.
[10] 王伟珠. 线性方程组应用分析[J]. 现代商贸工业, 2016(36): 168-169.
【通联编辑:王力】
收稿日期:2021-03-22
基金项目:湖南省普通高等学校教学改革研究项目“基于学科竞赛驱动培养地方院校数学类应用型创新人才的研究与实践”(湘教通[2018]436号No.732);湖南人文科技学院MOOC/SPOC课程建设项目“MATLAB语言基础”(校教通〔2018〕85号No. 21)
作者簡介:聂奥洋(2001—),男,湖南娄底人,本科生,主要研究方向为数学建模及其应用;通信作者:李军成(1982—),男,湖北省汉川市人,教授,博士,主要研究方向为几何设计与计算、数学建模。

