基于EDF的实时任务带宽转让研究综述
钱光明 邓朝丰
摘要:实时任务带宽转让问题在网络通信和机器人目标逼近等许多场合具有应用背景。当新任务插入或老任务加速时,可能需要某些现行任务转让带宽。该文从三个方面对这个问题进行综述。一是如何进行压缩任务的选择,以便尽快而安全地实现这种转让;二是如何求出最早的安全转让时刻;三是有关算法的收敛问题。这三个方面都是基于最早截止期优先算法来展开研究的。
關键词:带宽转让;安全转让时刻;实时任务;选择性压缩;最早截止期优先
中图分类号:TP393 文献标识码:A
文章编号:1009-3044(2021)31-0060-02
1 引言
本文的任务“带宽”指的是任务的“使用率”。对于周期性任务[τi(Ci,Ti)]而言,其使用率[Ui=Ci/Ti],[Ti]是任务周期,[Ci]是每周期所需执行时间(执行量),[i]属于非负整数集。一个实时系统的全部带宽看作1,即100%。如果所有任务的周期和执行量都恒定不变,那么,只要它们的带宽之和不超过1,就是EDF(Earliest Deadline First)可调度的[1]。但是,在进行带宽转让时,即某些老任务(现行任务)出让带宽,以应对新任务的插入或其它老任务的加速要求时,即使所有任务带宽之和不大于1,也可能出现不可调度的情况(超截止期)[2]。所谓带宽转让,就是压缩某个或某些现行任务(延长其执行周期),使其让出部分带宽用于新的带宽需求,例如,将[τi(Ci,Ti)]的周期延长为[T'i],其使用率会降低为[U'i=Ci/T'i],从而让出的带宽为
[Ui-U'i=Ci/Ti-Ci/T'i.] (1)
(1)式的带宽可以全部用于新任务插入或老任务加速。文献[3]已经证明老任务加速可以等效为新任务插入来处理。实现这种带宽转让时,如何避免出现超截止期,研究由此展开。不会导致截止期丢失的新任务插入称为平滑插入,相应的插入时刻称为平滑插入时刻[δ][3],最早平滑插入时刻表示为[δearliest][4]。
2 转让任务的选择
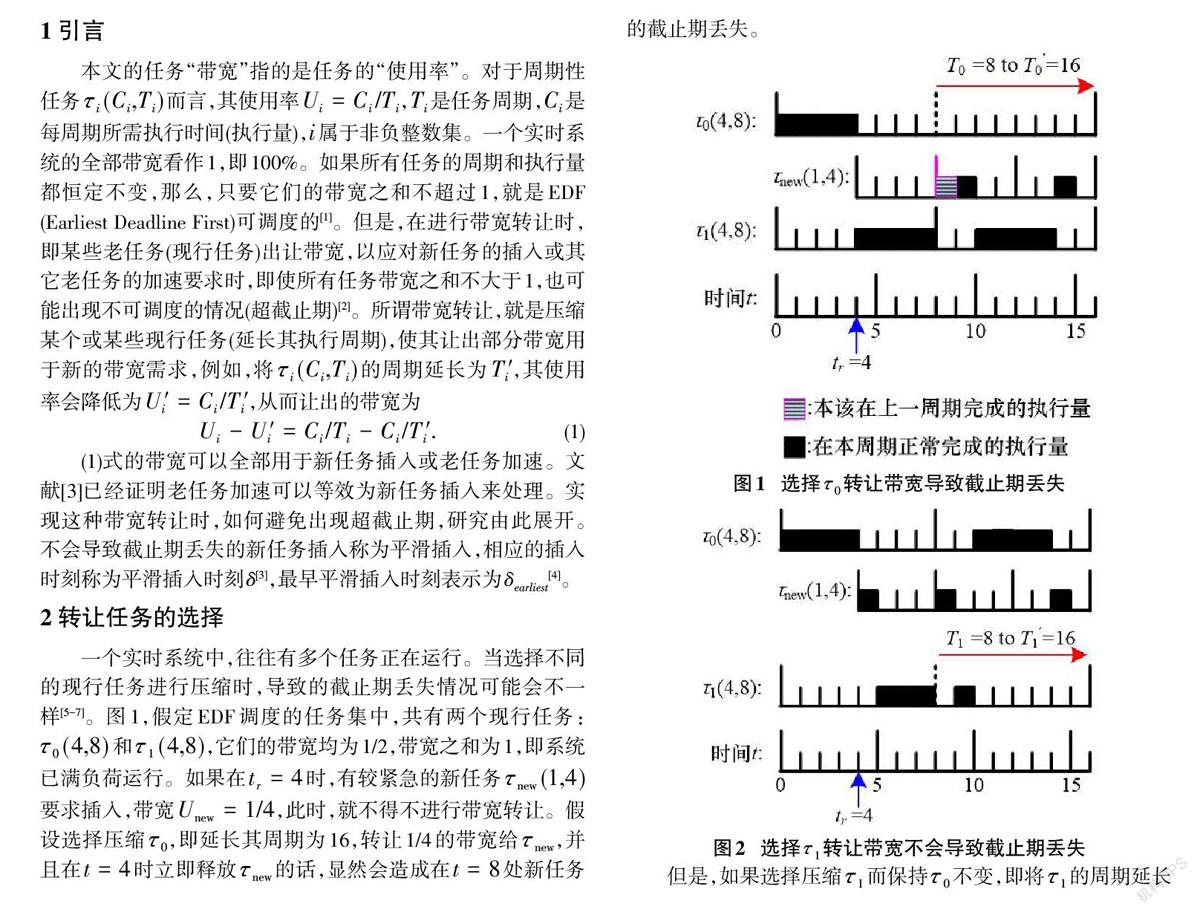
一个实时系统中,往往有多个任务正在运行。当选择不同的现行任务进行压缩时,导致的截止期丢失情况可能会不一样[5-7]。图1,假定EDF调度的任务集中,共有两个现行任务:[τ0(4,8)]和[τ1(4,8)],它们的带宽均为1/2,带宽之和为1,即系统已满负荷运行。如果在[tr=4]时,有较紧急的新任务[τnew(1,4)]要求插入,带宽[Unew=1/4],此时,就不得不进行带宽转让。假设选择压缩[τ0],即延长其周期为16,转让1/4的带宽给[τnew],并且在[t=4]时立即释放[τnew]的话,显然会造成在[t=8]处新任务的截止期丢失。
但是,如果选择压缩[τ1]而保持[τ0]不变,即将[τ1]的周期延长为16,则新任务在[t=4]时的插入不会导致任何截止期丢失,如图2所示。因此,图2中的[t=4]是一个平衡插入时刻。
带宽转让时,截止期丢失与否,与选择的压缩任务有关,这便是文献[5]提出的选择性压缩思想。文献[6]和[7]进一步对这一思想进行深入研究,提出了一个最晚截止期优先的带宽转让算法:在[tr]所处的周期中,在可压缩任务集内,先压缩当前作业截止期最晚的任务。这样做往往可以取得非常满意的效果。因为截止期最晚的任务往往是剩余执行量和剩余带宽较大的任务[6],可以立即出让较大比例的带宽。
3 最早安全转让时刻的求取
最早安全转让时刻(新任务平滑插入时刻) [δearliest]的求取,一直是一个令人感兴趣的挑战性问题[8-9]。对于任务周期等于截止期的研究模型,只压缩任务[τi(Ci,Ti)]时,文献[2]提出公式(2)用于平滑插入时刻的计算:
[δi=Ti—ci(tr)/Ui.] (2)
(2)式中[ci(tr)]是任务[τi]开始压缩时,当前周期的剩余执行量。该式表明:[τi]的出让带宽从[δi]开始,一定可以完全被新任务使用而不会引起截止期丢失。通过进一步深入研究,文献[3]提出了公式(3):
[δi=Ti—ci(tr)/(Ui—U'i).] (3)
很明显,公式(3)算出的[δi]要等于或早于公式(2)的值。例如,图1中,假定在[tr=3]时开始压缩[τ0(4,8)],其周期延长为16,剩余执行量为[c0(tr)=1],那么,由(2)式和(3)式算得的[δi]分别为6和4。如果将压缩起点设定为[tr=4],则剩余执行量为[c0(tr)=0],由(2)式和(3)式算得的[δi]均为8。
无论是公式(2)和公式(3),算出的[δi]都不能保证是最早平滑插入时刻[δearliest]。后续文献为计算[δearliest]做出了努力。文献[10]研究的模型设定为任务对:即老任务[τi(Ci,Ti)]出让带宽给一个新任务[τj(Cj,Tj)],而任何时间段为其它任务留下的带宽都等于它们的使用率之和。该模型的最早平滑插入时刻计算式为
[δjest=t0+Ti—(n+1)Tj+(n+1)Cj-ci(tr)Ui.] (4)
公式(4)中,[t0]代表任务[τi]现行作业周期的起点时刻,[n]的计算则要分情况讨论,与新任务在[Ti]前的处理器需求以及[ci(tr)]有关[10]。以图1为例,设[tr=4],则[n=ci(tr)/Cj=01=0],代入(4)式得
[δjest=0+8—(0+1)4+(0+1)×1-012=6.]
與(2)式和(3)式算得的结果比对可知:(4)式得出的[δjest=6]要更早。
但是,(4)式对应的模型没有考虑任务对以外的其它任务的抢占情况,换言之,其它任务并不一定要求所有时间段都需要等于其使用率之和的带宽。只有全面考虑这一因素后,才能得出真正的[δearliest]。文献[4]作了较全面考虑,提出了一个ESITforSNT (Earliest Smooth Insertion Time for Single New Task)算法,用于计算单个新任务插入时真正的[δearliest]。ESITforSNT算法也要分两种情况计算[δearliest],对于图1设[tr=4]的话,有
[δearliest=tr+T1—(tr+T1—trTjTj)+Δ(tr,T1)+Δ(tr,T1)—CjCj(Tj—Cj)]
[=4+8—(4+8—44×4)+1+1—11(4—1)=5.] (5)
(5)式得出的[δearliest=5]是真正的最早平滑插入时刻,要比(4)式的[δjest=6]更早。式中的[Δ(tr,T1)]代表从[t=tr]到[t=T1]间的[Δ]检查值[4]。更详细的描述可参考文献[4]。
4 算法的收敛问题
如果不考虑时间复杂度的因素,求取[δearliest]最朴素的方法是离线法[11]:先设[δearliest=tr]进行测试,如果插入新任务后系统不出现超截止期,则真正的[δearliest]就是[tr],测试停止;否则设[δearliest=δearliest+tstep]再进行下一轮测试。这样的测试可能要经过很多轮。文献[11]中步长[tstep]取值为1。
这样的测试方法的复杂度,主要与两个因素有关:一是[tstep]的取值;二是每次测试时,要检查的最大截止期点,即到底要检查到什么时间点才算结束,也就是算法的收敛条件。
文献[12]证明了一个准则:如果测试时某点截止期丢失,到下一轮的[tstep]取值至少不小于此时的[Δ]检查值(可能大于1)。对于降低算法复杂度,这个准则显然具有重要贡献。
文献[11]给出了算法的三个收敛条件:即试探到公倍点、试探到截止期对齐和试探到较小的剩余使用率。进一步,后续文献证明了截止期丢失只可能出现在时间段[[d'min,d'max)]中[12-14]。[d'min]和[d'max]分别代表[tr]所处当前周期中,所有受压任务的最早和最晚截止期点。这样,每次测试时,只要从[d'min]试探到[d'max]即可。对于快速求取[δearliest],这个结论具有重要意义。
5 结束语
关于实时任务带宽转让问题,虽然依上所述取得了不错的成果,但仍然有待深入研究。今后的研究思路主要有以下几点:(1)需要压缩多个任务进行带宽转让时,有必要寻找更好的选择策略以实现快速转让。(2)关于[δearliest]的求取,ESITforSNT算法只是针对单个新任务。多个新任务压缩时,如何快速求取[δearliest],仍然需要探索。(3)算法的收敛条件也需要继续深入研究。例如,如果[d'max]数值太大,且在[[d'min,d'max)]间截止期点过多,也会延长获得[δearliest]的测试时间。(4)如果作业的截止期点不是任务周期的结束点,或是干脆有的任务不是周期性的,那么,模型的建立和[δearliest]的求取将会更加复杂。
参考文献:
[1] Liu C L,Layland J W.Scheduling algorithms for multiprogramming in a hard-real-time environment[J].Journal of the ACM,1973,20(1):46-61.
[2] Buttazzo G C,Lipari G,Caccamo M,et al.Elastic scheduling for flexible workload management[J].IEEE Transactions on Computers,2002,51(3):289-302.
[3] Qian G M.An earlier time for inserting and/or accelerating tasks[J].Real-Time Systems,2009,41(3):181-194.
[4] Qian G M.The earliest smooth release time for a new task based on EDF algorithm[J].IEEE Access,2020,8:220595-220605.
[5] 钱光明,陈湘华,姜辉.实时任务的选择性压缩[J].湖南文理学院学报(自然科学版),2011,23(1):67-70,80.
[6] 钱光明,杨扬.最晚截止期优先带宽转让算法[J].计算机工程,2013,39(9):137-141.
[7] 杨扬.基于EDF的带宽转让算法研究[D].长沙:湖南师范大学,2014.
[8] Pillai P, Shin K G. Real-Time Dynamic Voltage Scaling for Low-Power[C].In Proc. 18th ACM Symposium, Operating Systems Principles, Banff, Canada, Aug., 2001: 89-102.
[9] Casini D,Biondi A,Buttazzo G.Handling transients of dynamic real-time workload under EDF scheduling[J].IEEE Transactions on Computers,2019,68(6):820-835.
[10] 钱光明,周垠宇.基于最早截止期优先算法的任务对带宽转让研究[J].计算机工程,2016,42(4):65-69.
[11] 钱光明,姜辉,陈湘华.实时任务调度算法最早可行时刻的求取模式[J].计算机工程,2012,38(4):284-286.
[12] QIAN Guangming, SU Shen. Method to Evaluate Earliest Release Time of New Real-time Tasks[J]. Computer Engineering,2018, 44(12): 62-67.
[13] 钱光明.基于最早截止期优先算法的过渡过程研究[J].计算机工程,2014,40(9):55-58.
[14] 钱光明,梁丽稳.实时多任务带宽转让的过渡过程研究[J].计算机工程,2017,43(12):292-295,302.
【通联编辑:代影】
收稿日期:2021-03-20
基金项目:长沙市科技局资助项目(ZD1802001)
作者简介:钱光明,男,教授,主要研究方向为嵌入式和实时系统;邓朝丰,男,在读研究生。

